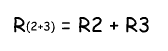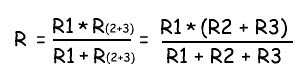Параллельное соединение резисторов. Калькулятор для расчета. Соединения резисторов схемыСоединение резисторов - Основы электроникиСоединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.
Рисунок 1. Соединение резисторов. Последовательное соединение резисторовПоследовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).
Рисунок 2. Последовательное соединение резисторов. То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток. Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле: Rобщ = R1 + R2 + R3+...+ Rn. Параллельное соединение резисторовПараллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).
Рисунок 3. Параллельное соединение резисторов. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn Следует отметить, что здесь действует правило «меньше - меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле: Rобщ= R1*R2/R1+R2 Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Смешанное соединение резисторовСмешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением. На рисунке 4 показан простейший пример смешанного соединения резисторов.
Рисунок 4. Смешанное соединение резисторов. На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно. Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.4. Рассчитывают сопротивления полученной схемы. Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.
Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов. ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! Похожие материалы:Добавить комментарийwww.sxemotehnika.ru Смешанное соединение резисторовСодержание:
Резистор представляет собой устройство, обладающее устойчивым, стабильным значением сопротивления. Это позволяет выполнять регулировку параметров на любых участках электрической цепи. Существуют различные виды соединений, в том числе и смешанное соединение резисторов. От использования того или иного способа в конкретной схеме, напрямую зависит падение напряжений и распределение токов в цепи. Вариант смешанного соединения состоит из последовательного и параллельного подключения активных сопротивлений. Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы. Последовательное соединениеПоследовательная схема подключения предполагает расположение резисторов в схеме таким образом, что конец первого элемента соединяется с началом второго, а конец второго – с началом третьего и т.д. То есть все резисторы поочередно следуют друг за другом. Сила тока при последовательном соединении будет одинаковой в каждом элементе. В виде формулы это выглядит следующим образом: Iобщ = I1 = I2, где Iобщ является общим током цепи, I1 и I2 – соответствуют токам 1-го и 2-го резистора. В соответствии с законом Ома, напряжение источника питания будет равно сумме падений напряжения на каждом резисторе: Uобщ = U1 + U2 = I1r1 + I2r2, в которой Uобщ – напряжение источника электроэнергии или самой сети; U1 и U2 – значение падений напряжения на 1-м и 2-м резисторах; r1 и r2 – сопротивления 1-го и 2-го резисторов. Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r1 + r2). Таким образом, можно сделать вывод, что при последовательной схеме включения резисторов, электрический ток, протекающий через каждый из них равен общему значению тока во всей цепи. Напряжение на каждом резисторе будет разное, однако их общая сумма составит значение, равное общему напряжению всей электрической цепи. Общее сопротивление цепи также будет равно сумме сопротивлений каждого резистора, включенного в эту цепь. Параметры цепи при параллельном соединенииПараллельное соединение представляет собой включение начальных выходов двух и более резисторов в единой точке, и концов этих же элементов в другой общей точке. Таким образом, фактически происходит соединение каждого резистора непосредственно с источником электроэнергии. В результате, напряжение каждого резистора будет одинаковым с общим напряжением цепи: Uобщ = U1 = U2. В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2. Для расчетов общего сопротивления используется формула: . Она используется при наличии в цепи только двух сопротивлений. В тех случаях, когда сопротивлений в цепи подключено три и более, применяется другая формула: Таким образом, значение общего сопротивления электрической цепи будет меньше, чем самое минимальное сопротивление одного из резисторов, подключенных параллельно в эту цепь. На каждый элемент поступает напряжение, одинаковое с напряжением источника электроэнергии. Распределение тока будет прямо пропорциональным сопротивлению резисторов. Значение общего сопротивления резисторов, соединенных параллельно, не должно превышать минимального сопротивления какого-либо элемента. Схема смешанного соединения резисторовСхема смешанного соединения обладает свойствами схем последовательного и параллельного соединения резисторов. В этом случае элементы частично подключаются последовательно, а другая часть соединяется параллельно. На представленной схеме резисторы R1 и R2 включены последовательно, а резистор R3 соединен параллельно с ними. В свою очередь резистор R4 включается последовательно с предыдущей группой резисторов R1, R2 и R3. Расчет сопротивления для такой цепи сопряжен с определенными трудностями. Для того чтобы правильно выполнить расчеты используется метод преобразования. Он заключается в последовательном преобразовании сложной цепи в простейшую цепь за несколько этапов. Если для примера вновь использовать представленную схему, то в самом начале определяется сопротивление R12 резисторов R1 и R2, включенных последовательно: R12 = R1 + R2. Далее, нужно определить сопротивление резисторов R123, включенных параллельно, по следующей формуле: R123=R12R3/(R12+R3) = (R1+R2)R3/(R1+R2+R3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4. В заключение следует отметить, что смешанное соединение резисторов обладает положительными и отрицательными качествами последовательного и параллельного соединения. Это свойство успешно используется на практике в электрических схемах. Схемы соединения резисторовПоследовательное соединение резисторов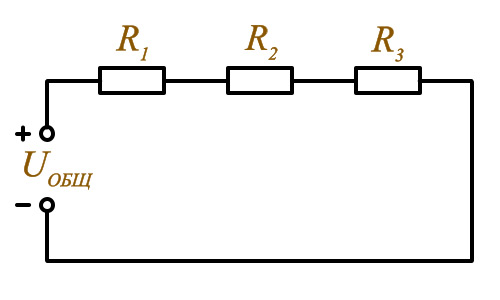 Последовательное соединение резисторов
Iобщ = I1 = I2 = I3 Uобщ = U1 + U2 + U3 Параллельное соединение резисторов 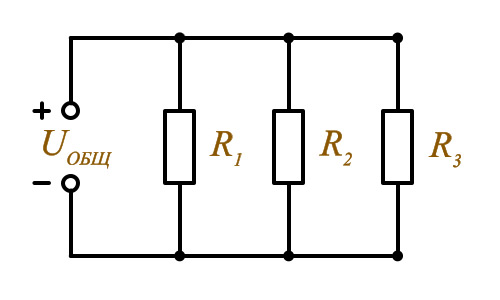 Параллельное соединение резисторов
Iобщ = I1 + I2 + I3 Uобщ = U1 = U2 = U3 Реостат Реостат – это переменный резистор, который включается в цепь последовательно с потребителем нагрузки. Изменяя положение ползунка, в цепи меняется ток от 0 до max. Реостат применяется для изменения тока в цепи. В электрических схемах встречается понятие – реостатное включение нагрузки. 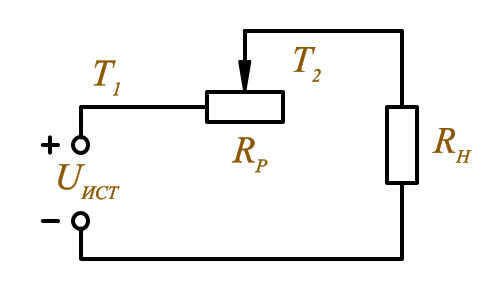 Реостатное включение нагрузки
RP = 0
В радиосхемах возникает необходимость подавать на потребитель напряжение меньше чем развивает источник, тогда между источником и нагрузкой включается гасящий резистор. Применение – в схеме создания напряжения смещения на участке эмиттер-база транзистора.  Гасящий резистор
Uгас = Uист – URн
PRгас = I2 – Rгас Делитель напряжения Делитель напряжения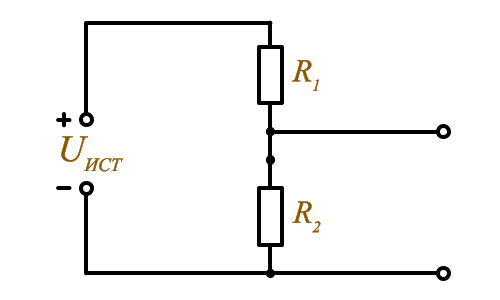
Делитель напряжения – это цепь, состоящая из нескольких последовательно соединённых резисторов обеспечивающих подачу на потребитель некоторой части напряжения источника. Потенциометр – это переменный резистор, с части которого снимается напряжения источника. 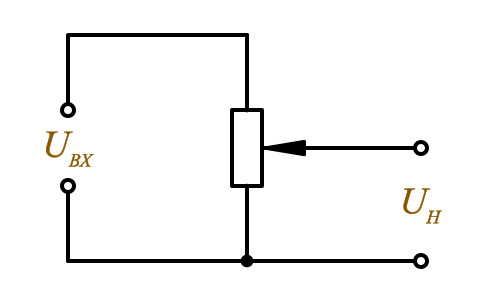 Потенциометр
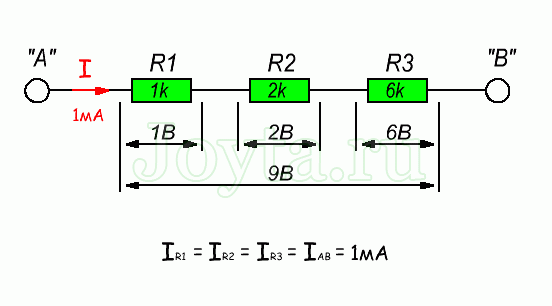
Применение – регулировка громкости на входе усилителя низкой частоты. selectelement.ru Последовательное соединение резисторов. Схема соединения и примеры расчетаВо многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление. Последовательное соединении резисторов - это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи. Последовательное соединение резисторовНа рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.
Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле: R = R1 + R2 + R3 То есть, в нашем случае общее сопротивление цепи будет равно: R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.
Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов. Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3). Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:
Используя закон Ома , напряжение на отдельных резисторов может быть вычислена следующим образом:
В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В. В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:
Пример № 1Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2Необходимо рассчитать падение напряжения на выводах "А" и "В": а) без подключенного резистора R3 б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке. Онлайн калькулятор расчета сопротивления последовательно соединенных резисторовЧтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором: Подведем итогКогда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) - то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R). www.joyta.ru Последовательное и параллельное соединение резисторов.Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения резисторов, в частности о последовательном соединении и о параллельном.
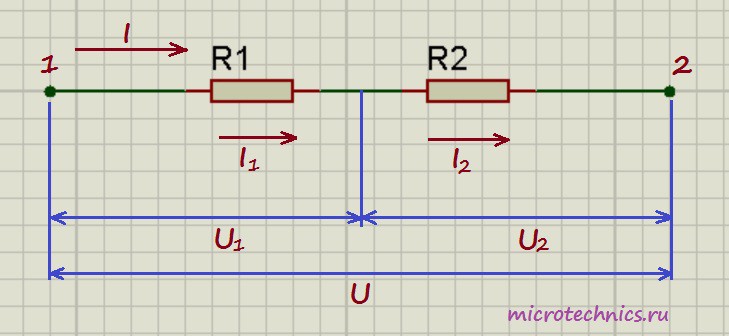
Последовательное соединение резисторов.Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно будет использовать следующее выражение:
Но для общего напряжение также справедлив закон Ома:
Здесь
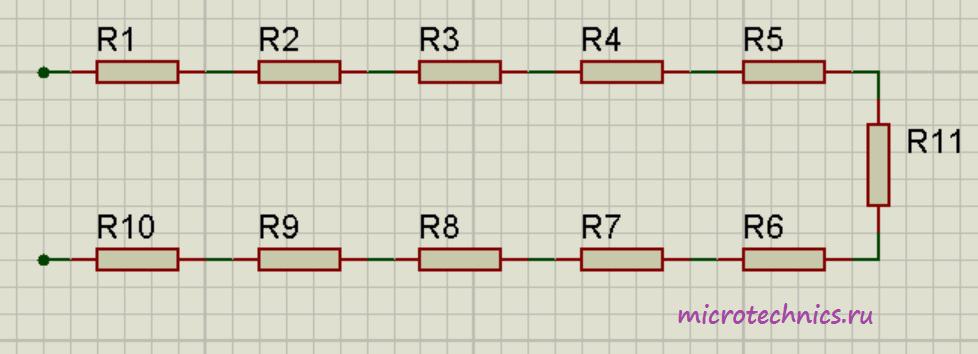
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников. Например для следующей цепи:
Общее сопротивление будет равно:
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление будем работать в любом случае 🙂 А если при последовательном соединении все сопротивления равны (
С последовательным соединением резисторов мы разобрались, давайте перейдем к параллельному. Параллельное соединение резисторов.
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
Подставим эти выражения в формулу общего тока:
А по закону Ома ток:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
Данную формулу можно записать и несколько иначе:
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников. Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
Смешанное соединение резисторов.Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
Давайте рассчитаем общее сопротивление цепи. Начнем с резисторов
Теперь у нас образовались две группы последовательно соединенных резисторов:
Заменим эти две группы двумя резисторами, сопротивление которых равно:
Как видите, схема стала уже совсем простой ) Заменим группу параллельно соединенных резисторов
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
Общее сопротивление цепи получилось равным:
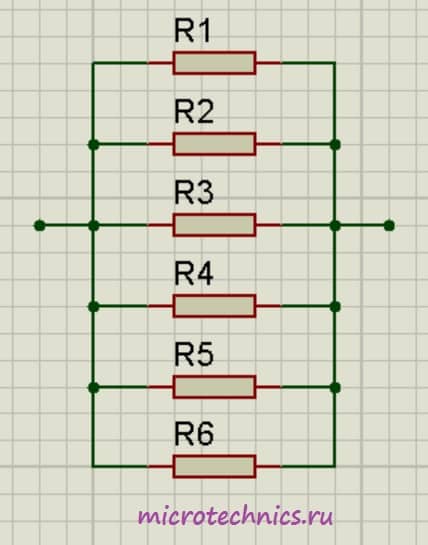
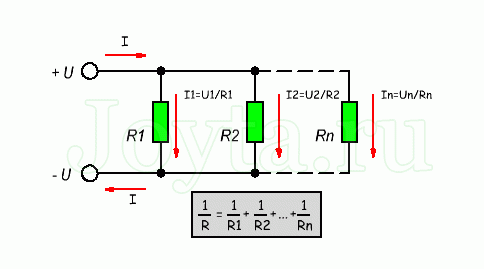
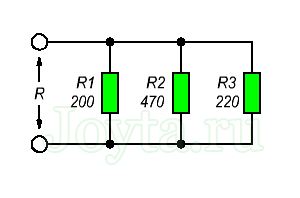
Таким вот образом достаточно большая схема свелась к простейшему последовательному соединению двух резисторов 😉 Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте! microtechnics.ru Параллельное соединение резисторов. Калькулятор для расчетаПараллельное соединение резисторов - одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы. Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторовОбщее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Параллельное соединение резисторов - расчетПример №1При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет. Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом. Пример расчета №2Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно. Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации. Как рассчитать сложные схемы соединения резисторовБолее сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
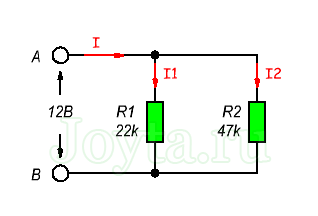
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа. Ток, протекающий в цепи параллельно соединенных резисторахОбщий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях. Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома). Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке "B" .
Первое правило Кирхгофа гласит: "Общий ток, выходящий из цепи равен току входящий в цепь". Таким образом, протекающий общий ток в цепи можно определить как: I = I1 + I2 Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор: Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА Таким образом, общий ток будет равен: I = 0,545 мА + 0,255 мА = 0,8 мА Это также можно проверить, используя закон Ома: I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое) где 15кОм - это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм) И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь. Параллельное соединение резисторов - онлайн калькуляторЧтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором: Подведем итогКогда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора. Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение. www.joyta.ru Расчет сопротивления схемы с преобразованием треугольник-звезда.Рассмотрим схему приведенную на рисунке 1:Рисунок 1 - Исходная схема Допустим необходимо найти сопротивление схемы относительно точек A и B. Заданы сопротивления резисторов: R1=20, R2=20, R3=10, R4=20, R5=8, R6=4, R7=4. Преобразуем треугольник сопротивлений R1, R2, R3 в звезду сопротивлений R12, R23, R13: Рисунок 2 - Схема с преобразованным в звезду треугольником Сопротивления R12, R13, R23 найдены по формулам 1-3: Чтобы найти сопротивление луча звезды надо произведение сопротивлений прилегающих к нему сторон треугольника разделить на сумму сопротивлений всех сторон треугольника. Преобразуем последовательное соединение резисторов R13 и R6 в резистор R136 и аналогично преобразуем последовательное соединение резисторов R23 и R7 в резистор R237: Рисунок 3 - Схема3 Сопротивления резисторов R136 и R237 найдены по формулам 4 и 5: Преобразуем параллельное соединение резисторов R136 и R237 в резистор R136IIR237: Рисунок 4 - Схема4 Найдем R136IIR237 по формуле 6: Далее преобразуем схему 4 к виду: Рисунок 5 - Схема5 Найдем сопротивление которое стоит справа: Теперь, заменой параллельного соединения резисторов, в схеме на рисунке 5, одним резистором Rэ, находится эквивалентное сопротивление всей схемы: Найдем Rэ: Преобразование треугольника R1, R2, R3 в звезду R12, R23, R13 упростило расчёт эквивалентного сопротивления схемы относительно точек А и B в данном примере.electe.blogspot.com |
|
||||||||||||||||||
|
|
||||||||||||||||||
|
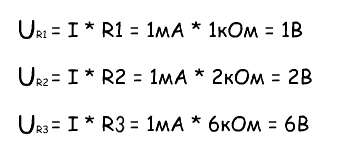
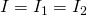
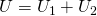
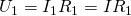
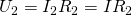
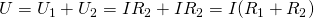
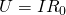
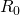– это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно: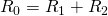
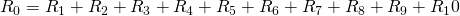
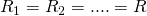), то общее сопротивление цепи составит: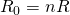
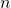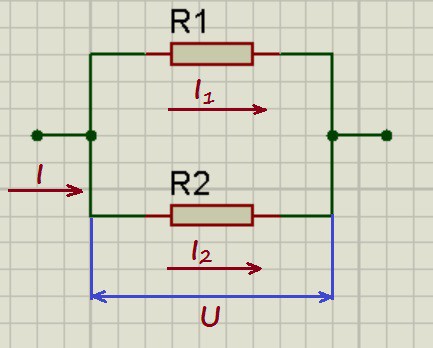
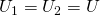
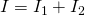
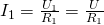
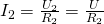
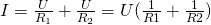
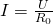
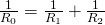
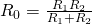
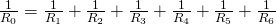
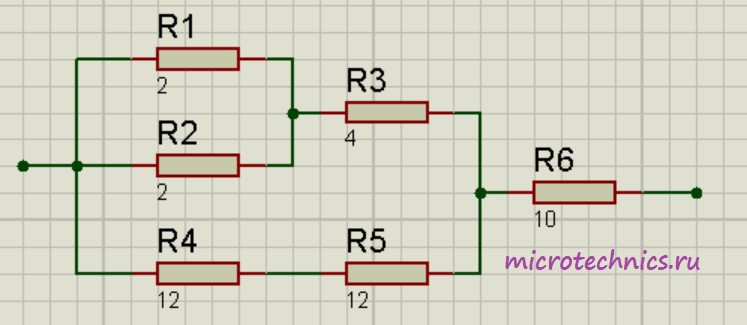
в данной формуле равно количеству элементов цеп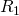и.
и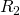 
– они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором 
:
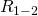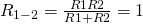
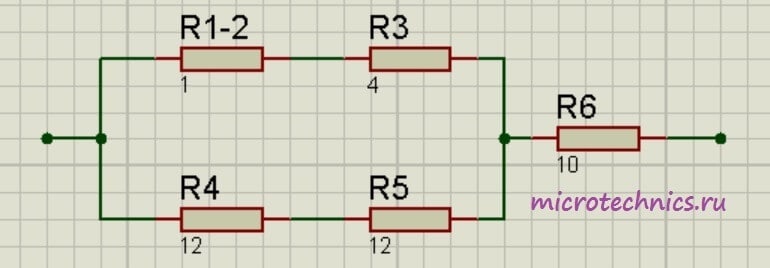
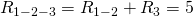
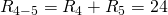
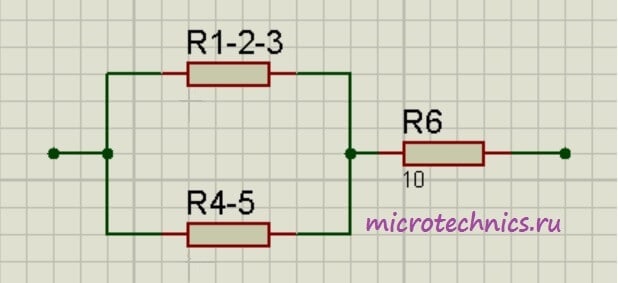
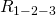и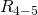 
одним резистором 
:
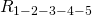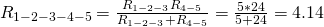
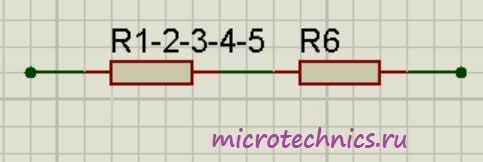
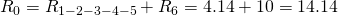
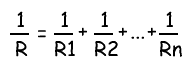
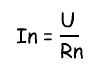
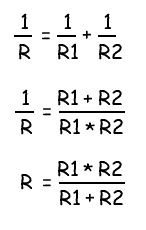
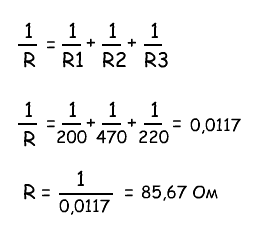
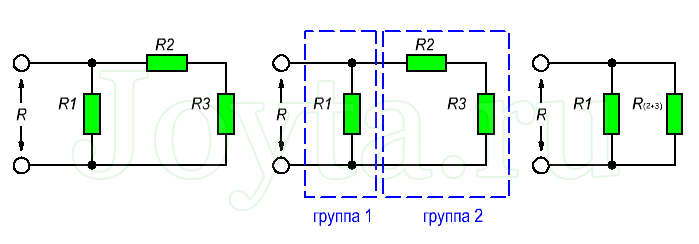Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
