коэффициент мощности цепи. Коэффициент мощности цепикоэффициент мощности цепи — с русскогоСм. также в других словарях:
translate.academic.ru Коэффициент мощности - это... Что такое Коэффициент мощности?Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны — между ними нет фазового сдвига (, ) — нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 1. Как видно, синяя линия (график мгновенной мощности) находится полностью над осью абсцисс (в положительной полуплоскости), вся подводимая энергия преобразуется в работу: переходит в активную мощность, потребляемую нагрузкой. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг () — нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0. Расположение синей линии (графика мгновенной мощности) на оси абсцисс показывает, что в течение первой четверти цикла вся подводимая мощность временно сохраняется в нагрузке, а во второй четверти цикла возвращается в сеть, и так далее, то есть никакой активной мощности не потребляется, полезной работы в нагрузке не совершается. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг () — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения. Численно коэффициент мощности равен косинусу этого фазового сдвига. Можно показать, что если источник синусоидального тока (например, розетка ~220 В, 50 Гц) нагрузить на нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше энергии; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным. Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт). Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %). Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы. В электроэнергетике для коэффициента мощности приняты обозначения cos φ (где φ — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ, его величину обычно выражают в процентах. При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим. В случае синусоидального напряжения, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой, и равен коэффициенту искажений тока. Математические расчётыТреугольник мощностейКоэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети. Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы: Здесь — активная мощность, — полная мощность, — реактивная мощность. Типовые оценки качества электропотребленияКоэффициент мощности позволяет судить о нелинейных искажениях, вносимых нагрузкой в электросеть. Чем он меньше, тем больше вносится нелинейных искажений. Кроме того, при одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.
Например, большинство компактных люминесцентных («энергосберегающих») ламп, имеющих ЭПРА, характеризуются высоким его значением. Нелинейные искажения токаПотребители электроэнергии с нелинейной вольтамперной характеристикой (с коэффициентом мощности, меньшим единицы) создают ток, который меняется непропорционально мгновенному напряжению в сети (как правило, форма тока при этом отличается от синусоидальной). Соответственно искажается форма напряжения на данном участке электросети, что приводит к ухудшению качества электроэнергии. В зависимости от характера нагрузки можно выделить следующие основные виды нелинейных искажений тока: это фазовый сдвиг, вызванный реактивной составляющей в нагрузке, и несинусоидальность формы тока. Несинусоидальные искажения, в частности, имеют место, когда нагрузка несимметрична в разных полуволнах сетевого напряжения. НесинусоидальностьНесинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счёт мощности искажения, вызванной протеканием токов высших гармоник; а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности. Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы и др. Ссылкиbiograf.academic.ru коэффициент мощности цепи - это... Что такое коэффициент мощности цепи? коэффициент мощности цепи3.12 коэффициент мощности цепи: Отношение измеренной потребляемой активной мощности к произведению среднеквадратических значений питающего напряжения и потребляемого тока. 3.14 коэффициент мощности цепи; (circuit power factor; λ):Коэффициент мощности комплекта устройств управления лампами и ламп, для которых предназначено устройство управления лампами. 3.2 коэффициент мощности цепи; A, (circuit power factor; X): Отношение значения измеренной мощности цепи к произведению действующих значений напряжения и тока сети. Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
Смотреть что такое "коэффициент мощности цепи" в других словарях:
normative_reference_dictionary.academic.ru Коэффициент мощности - это... Что такое Коэффициент мощности?Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны — между ними нет фазового сдвига (, ) — нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 1. Как видно, синяя линия (график мгновенной мощности) находится полностью над осью абсцисс (в положительной полуплоскости), вся подводимая энергия преобразуется в работу: переходит в активную мощность, потребляемую нагрузкой. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг () — нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0. Расположение синей линии (графика мгновенной мощности) на оси абсцисс показывает, что в течение первой четверти цикла вся подводимая мощность временно сохраняется в нагрузке, а во второй четверти цикла возвращается в сеть, и так далее, то есть никакой активной мощности не потребляется, полезной работы в нагрузке не совершается. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг () — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения. Численно коэффициент мощности равен косинусу этого фазового сдвига. Можно показать, что если источник синусоидального тока (например, розетка ~220 В, 50 Гц) нагрузить на нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше энергии; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным. Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт). Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %). Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы. В электроэнергетике для коэффициента мощности приняты обозначения cos φ (где φ — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ, его величину обычно выражают в процентах. При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим. В случае синусоидального напряжения, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой, и равен коэффициенту искажений тока. Математические расчётыТреугольник мощностейКоэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети. Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы: Здесь — активная мощность, — полная мощность, — реактивная мощность. Типовые оценки качества электропотребленияКоэффициент мощности позволяет судить о нелинейных искажениях, вносимых нагрузкой в электросеть. Чем он меньше, тем больше вносится нелинейных искажений. Кроме того, при одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.
Например, большинство компактных люминесцентных («энергосберегающих») ламп, имеющих ЭПРА, характеризуются высоким его значением. Нелинейные искажения токаПотребители электроэнергии с нелинейной вольтамперной характеристикой (с коэффициентом мощности, меньшим единицы) создают ток, который меняется непропорционально мгновенному напряжению в сети (как правило, форма тока при этом отличается от синусоидальной). Соответственно искажается форма напряжения на данном участке электросети, что приводит к ухудшению качества электроэнергии. В зависимости от характера нагрузки можно выделить следующие основные виды нелинейных искажений тока: это фазовый сдвиг, вызванный реактивной составляющей в нагрузке, и несинусоидальность формы тока. Несинусоидальные искажения, в частности, имеют место, когда нагрузка несимметрична в разных полуволнах сетевого напряжения. НесинусоидальностьНесинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счёт мощности искажения, вызванной протеканием токов высших гармоник; а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности. Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы и др. Ссылкиdikc.academic.ru Мощность в цепях переменного тока. Коэффициент мощности и его технико-экономическое значение.Поиск Лекций
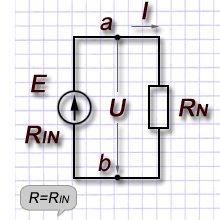
Коэффициент мощности и его технико-экономическое значение. Компенсация реактивной мощности Отношение активной мощности к полной показывает, какая доля полной мощности потребляется нагрузкой, и называется коэффициентом мощности.
Таким образом, коэффициент мощности численно равен cos φ. В качестве примера на рис. 51 показана зависимость силы тока от Рис. 51. Зависимость силы тока от cos φ при напряжении сети U=380 В и Р=500 кВт Из графика видно, что при снижении коэффициента мощности возрастает реактивная составляющая тока, а следовательно, возрастает общий ток линии. Генераторы, питающие потребители, рассчитывают на определенную номинальную мощность:
При заданном напряжении Чтобы ток генератора не был выше номинального при снижении Важным технико-экономическим показателем является и коэффициент реактивной мощности:
Коэффициент
Коэффициент мощности является недостаточным показателем для оценки реактивной составляющей нагрузки, особенно при высоких значениях коэффициента мощности, что видно из зависимостей реактивной мощности Q от коэффициента мощности Таблица 2 Из таблицы видно, что при достаточно высоком значении Чтобы повысить экономичность энергетических установок, принимают меры для уменьшения реактивной мощности в линии электропередачи. Коэффициент мощности при этом возрастает. Повышения коэффициента мощности промышленного предприятия можно достигнуть лишь правильным сочетанием направленных на это мероприятий, каждое из которых должно быть технически и экономически обосновано. Мероприятия по повышению коэффициента мощности можно разделить на следующие группы: 1) уменьшение потребления реактивной мощности приемникамиэлектрической энергии без применения компенсирующих устройств; 2) применение компенсирующих устройств. К первой группе мероприятий относятся: а) упорядочение технологического процесса, ведущее к улучшению энергетического режима оборудования; б) замена малозагруженных асинхронных двигателей двигателями мень-шей мощности; в) понижение напряжения питания асинхронных двигателей, систематически работающих с малой нагрузкой; г) ограничение режимов холостого хода двигателей и трансформаторов; д) повышение качества ремонта двигателей; е) замена малозагруженных трансформаторов трансформаторами мень-шей мощности. Для компенсации реактивной мощности, потребляемой электроустановками промышленного предприятия, могут быть применены синхронные компенсаторы и статические конденсаторы. Рассмотрим способ компенсации реактивной мощности статическими конденсаторами. На рис. 52 показаны асинхронные двигатели, являющиеся приемниками электрической энергии, и эквивалентная схема одной фазы, в которой обмотка статора асинхронного двигателя представлена активным и индуктивным сопротивлениями. В качестве компенсирующего устройства включены конденсаторы.
Рис. 52. Схема включения конденсаторов в качестве компенсаторов реактивной мощности при активно-индуктивной нагрузке (обмотки статора асинхронных двигателей) и эквивалентная схема одной фазы Активная мощность одной фазы приемника электроэнергии при заданном напряжении определяется активной составляющей тока Ia:
При заданном значении активной мощности активная составляющая тока должна оставаться неизменной. Наличие реактивной (индуктивной) составляющей тока приводит к увеличению фактического значения тока нагрузки и, как следствие, к увеличению потерь мощности. Снизить ток нагрузки можно только за счет уменьшения реактивной составляющей тока приемника. Последнее можно осуществить путем параллельного подключения приемника с емкостным элементом. Все сказанное наглядно иллюстрируется векторной диаграммой (рис. 53). Таким образом, c введением компенсирующего устройства уменьшается реактивная составляющая тока, а следовательно, уменьшаются полный ток При определении емкости конденсаторов, необходимых для понижения коэффициента реактивной мощности
Рис. 53. Векторная диаграмма, иллюстрирующая компенсацию индуктивной составляющей тока включением емкостного элемента
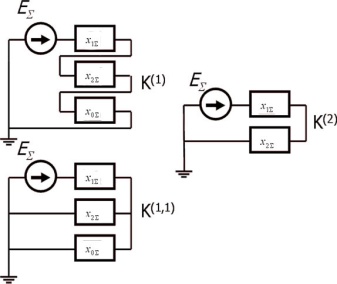
Комплексный метод расчета линейных цепей переменного тока. Комплексные схемы замещения электрических цепей. Комплексные сопротивления и проводимости ветвей. Комплексная мощность. В комплексном методе расчета линейных цепей переменного тока ЭДС, напряжения, токи, сопротивления, проводимости и мощности представляют в виде комплексов. Комплексные значения величин, изменяющихся по гармоническому закону, обозначают соответствующими прописными буквами, над которыми ставят точку: . Для обозначения модулей этих величин применяют те же буквы, но без точек над ними: E, U, I. Комплекс полного сопротивления обозначают прописной буквой Z (без точки), комплекс полной проводимости - буквой Y (без точки). Модули этих величин обозначают соответствующими строчными буквами z и у. Комплексные числа записываются в одной из следующих форм: = a + jb - алгебраическая форма; = А (cos+ j sin) - тригонометрическая форма; = А - показательная форма, где А = - модуль комплексного числа; - аргумент комплексного числа; - мнимая единица. Для расчета цепей синусоидального переменного тока комплексным методом применяются все методы, известные из теории электрических цепей постоянного тока. Всё отличие состоит в том, что вместо действительных чисел, соответствующим токам, напряжениям и сопротивлениям в цепях постоянного тока, при расчете цепей переменного тока используется комплексные числа. При умножении и делении комплексных чисел необходимо использовать показательную форму записи, а при сложении и вычитании - алгебраическую форму. Комплексная схема — это схема, полученная соединением схем замещения прямой, обратной и нулевой последовательностей. Способ соединения зависит от вида КЗ. Здесь каждый прямоугольник представляет собой схему замещения определенной последовательности. Соединить эти схемы замещения в комплексную схему — значит подключить к схеме прямой последовательности шунт КЗ, представляемый в комплексной схеме суммарными сопротивлениями обратной и нулевой последовательностей, которые определяются относительно начала и конца соответствующей схемы.
В итоге еще раз можно представить алгоритм расчета несимметричного КЗ в виде нескольких основных этапов: 1. Составляются схемы замещения прямой, обратной и нулевой последовательностей. 2. Производятся расчет и приведение параметров схемы замещения. При этом учитываются различия параметров прямой, обратной и нулевой последовательностей отдельных элементов схемы. 3. Определяются эквивалентные суммарные сопротивления схем прямой, обратной и нулевой последовательностей. Преобразования осуществляются относительно начала и конца схемы каждой последовательности. 4. Находится результирующая ЭДС схемы прямой последовательности. 5. Вычисляется коэффициент m рассчитываемого КЗ. 6. Определяется шунт короткого замыкания. 7. Рассчитывается полный ток в месте КЗ по выражению. 8. Строятся векторные диаграммы. Комплексное сопротивление Введение комплексного представления токов и напряжений требует определить и сопротивление элементов электрических цепей в комплексной форме - Z.
Комплексное сопротивление емкости определяется отношением:
Коэффициент 1/wC определяет величину сопротивления в Омах. Он обратно пропорционален частоте, называется емкостным сопротивлением и обозначается ХC, т.е.
Комплексное сопротивление индуктивности определяется отношением:
Коэффициент wL определяет величину сопротивления в Омах. Он пропорционален частоте, называется индуктивным сопротивлением и обозначается ХL, т.е.
Комплексная проводимость. В цепях постоянного тока проводимость резистора определяется отношением тока к напряжению:
Эта величина обратно пропорциональна сопротивлению. В цепях переменного тока следует пользоваться понятием комплексной проводимости, которая обозначается Y и, в общем случае, содержит действительную G и мнимую В части:
Как и в цепях постоянного тока комплексная проводимость участка цепи обратна комплексному сопротивлению, т.е.
Отсюда
где Y - модуль комплексной проводимости. Соотношение между составляющими комплексной проводимости аналогичны соотношениям между составляющими комплексного сопротивления. Комплексная проводимость резистора
Комплексная проводимость конденсатора
Комплексная проводимость индуктивности
Комплексная мощность Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть
где
poisk-ru.ru Коэффициент мощности - это... Что такое Коэффициент мощности?Синусоидальное напряжение (красная линия) и ток (зелёная линия) синфазны — между ними нет фазового сдвига (, ) — нагрузка полностью активная, нет реактивной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 1. Как видно, синяя линия (график мгновенной мощности) находится полностью над осью абсцисс (в положительной полуплоскости), вся подводимая энергия преобразуется в работу: переходит в активную мощность, потребляемую нагрузкой. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг () — нагрузка полностью реактивная, нет активной составляющей. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны с коэффициентом мощности, равным 0. Расположение синей линии (графика мгновенной мощности) на оси абсцисс показывает, что в течение первой четверти цикла вся подводимая мощность временно сохраняется в нагрузке, а во второй четверти цикла возвращается в сеть, и так далее, то есть никакой активной мощности не потребляется, полезной работы в нагрузке не совершается. Синусоидальное напряжение (красная линия) и ток (зелёная линия) имеют фазовый сдвиг () — нагрузка имеет и активную, и реактивную составляющие. Мгновенная мощность (синяя линия) и активная мощность (голубая линия) рассчитаны из переменного напряжения и тока с коэффициентом мощности, равным 0,71. Расположение синей линии (графика мгновенной мощности) под осью абсцисс показывает, что некоторая часть подводимой мощности всё же возвращается в сеть в течение части цикла, отмеченного φ.Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения. Численно коэффициент мощности равен косинусу этого фазового сдвига. Можно показать, что если источник синусоидального тока (например, розетка ~220 В, 50 Гц) нагрузить на нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше энергии; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным. Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощность расходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт). Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %). Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы. В электроэнергетике для коэффициента мощности приняты обозначения cos φ (где φ — сдвиг фаз между силой тока и напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ, его величину обычно выражают в процентах. При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим. В случае синусоидального напряжения, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой, и равен коэффициенту искажений тока. Математические расчётыТреугольник мощностейКоэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПД электрооборудования, питающегося от данной сети. Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы: Здесь — активная мощность, — полная мощность, — реактивная мощность. Типовые оценки качества электропотребленияКоэффициент мощности позволяет судить о нелинейных искажениях, вносимых нагрузкой в электросеть. Чем он меньше, тем больше вносится нелинейных искажений. Кроме того, при одной и той же активной мощности нагрузки мощность, бесполезно рассеиваемая на проводах, обратно пропорциональна квадрату коэффициента мощности. Таким образом, чем меньше коэффициент мощности, тем ниже качество потребления электроэнергии. Для повышения качества электропотребления применяются различные способы коррекции коэффициента мощности, то есть его повышения до значения, близкого к единице.
Например, большинство компактных люминесцентных («энергосберегающих») ламп, имеющих ЭПРА, характеризуются высоким его значением. Нелинейные искажения токаПотребители электроэнергии с нелинейной вольтамперной характеристикой (с коэффициентом мощности, меньшим единицы) создают ток, который меняется непропорционально мгновенному напряжению в сети (как правило, форма тока при этом отличается от синусоидальной). Соответственно искажается форма напряжения на данном участке электросети, что приводит к ухудшению качества электроэнергии. В зависимости от характера нагрузки можно выделить следующие основные виды нелинейных искажений тока: это фазовый сдвиг, вызванный реактивной составляющей в нагрузке, и несинусоидальность формы тока. Несинусоидальные искажения, в частности, имеют место, когда нагрузка несимметрична в разных полуволнах сетевого напряжения. НесинусоидальностьНесинусоидальность — вид нелинейных искажений напряжения в электрической сети, который связан с появлением в составе напряжения гармоник с частотами, многократно превышающими основную частоту сети. Высшие гармоники напряжения оказывают отрицательное влияние на работу системы электроснабжения, вызывая дополнительные активные потери в трансформаторах, электрических машинах и сетях; повышенную аварийность в кабельных сетях; уменьшение коэффициента мощности за счёт мощности искажения, вызванной протеканием токов высших гармоник; а также ограниченное применение батарей конденсаторов для компенсации реактивной мощности. Источниками высших гармоник тока и напряжения являются электроприёмники с нелинейными нагрузками. Например, мощные выпрямители переменного тока, применяемые в металлургической промышленности и на железнодорожном транспорте, газоразрядные лампы и др. Ссылкиmed.academic.ru |
|
||||||||||||||||||
|
|
||||||||||||||||||
|




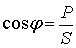 . (153)
. (153)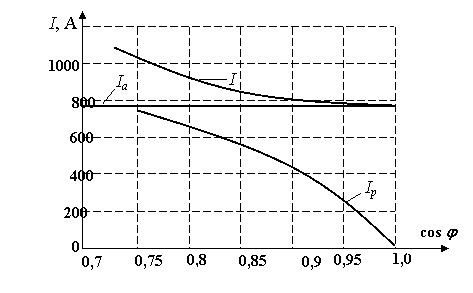
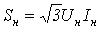 . (154)
. (154)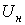 генератор может быть нагружен током, не превышающим номинальное значение
генератор может быть нагружен током, не превышающим номинальное значение 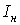 (
( 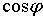 не должно превышать определенных пределов.
не должно превышать определенных пределов.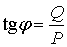 . (155)
. (155)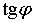 наглядно выражает реактивную мощность в долях от активной мощности. Связь между коэффициентом мощности и коэффициентом реактивной мощности выражается следующей зависимостью:
наглядно выражает реактивную мощность в долях от активной мощности. Связь между коэффициентом мощности и коэффициентом реактивной мощности выражается следующей зависимостью: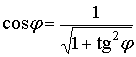 . (156)
. (156)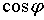 и коэффициента реактивной мощности
и коэффициента реактивной мощности 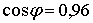 реактивная нагрузка составляет 29% от активной. Поэтому более показательным является коэффициент реактивной мощности
реактивная нагрузка составляет 29% от активной. Поэтому более показательным является коэффициент реактивной мощности 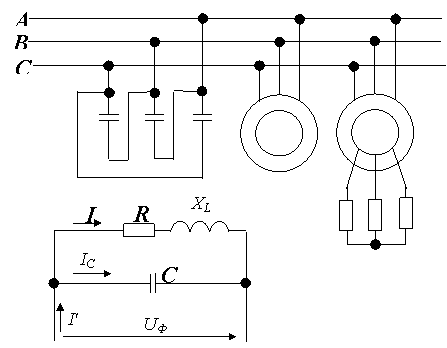
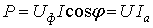 . (157)
. (157)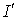 цепи и угол сдвига по фазе между напряжением и полным током цепи.
цепи и угол сдвига по фазе между напряжением и полным током цепи.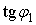 и после их установки
и после их установки 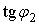 :
: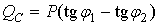 . (158)
. (158)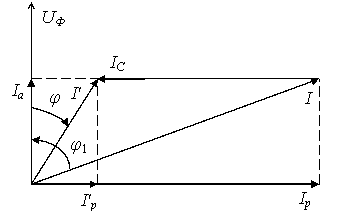

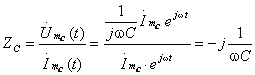 .
.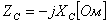
 .
.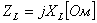
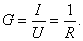
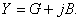
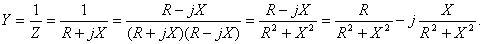
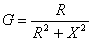 ,
, 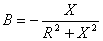 ,
, 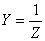 ,
,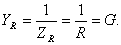
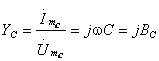 .
.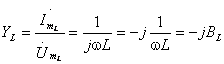 .
.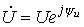 , а
, а 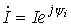 . Тогда комплекс полной мощности:
. Тогда комплекс полной мощности: 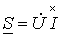
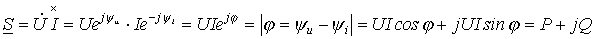
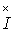 - комплекс, сопряженный с комплексом
- комплекс, сопряженный с комплексом 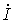 .
.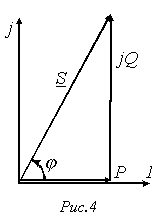 Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует
Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует 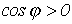 (активно-индуктивная нагрузка), для которого имеем
(активно-индуктивная нагрузка), для которого имеем