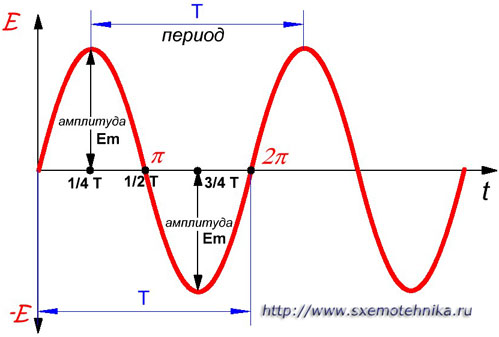
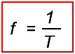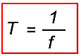Какова частота напряжения тока, а точнее частота электрического тока. Частота в электротехникеПериод, частота, амплитуда и фаза переменного токаПериод и частота переменного токаВремя, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период - время одного колебания; Аплитуда - его наибольшее мгновенное значение. Период выражают в секундах и обозначают буквой Т. Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды. 1 мс =0,001сек =10-3сек. 1 мкс=0,001 мс = 0,000001сек =10-6сек. 1000 мкс = 1 мс. Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока. Частота обозначается буквой f и выражается в периодах в секунду или в герцах. Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц. 1000 Гц = 103 Гц = 1 кГц; 1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц; 1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц; Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая. Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен: Т = 1/f = 1/50 = 0,02 сек. И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна: f = 1/T=1/0,02 = 100/2 = 50 Гц Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц. Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты. Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше. Амплитуда переменного токаНаибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1). Угловая (циклическая) частота переменного тока.Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах. Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
Рисунок 2. Радиан. Тогда, 1рад = 360°/2 Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2 Итак, ?= 6,28*f = 2f Фаза переменного тока.Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока. Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе. ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! Похожие материалы:Добавить комментарийwww.sxemotehnika.ru Частота электрического тока - это... Что такое Частота электрического тока? Частота электрического тока временной параметр периодически (циклически) изменяющегося электрического тока (См. Электрический ток), выражающийся отношением числа полных циклов изменения тока к единице времени; величина, обратная периоду изменения тока. Измеряется в Герцах. Для синусоидального переменного тока используют понятие угловой частоты (См. Угловая частота), связанной с Ч. э. т. соотношением ω = 2πf (ω — угловая частота, f — Ч. э. т.). Во многих странах мира (в т. ч. в СССР) частота промышленного тока, вырабатываемого электростанциями, равна 50 гц, в США — 60 гц. В ряде стран на железных дорогах используют ток частотой 16 2/3 гц (для электрической тяги), а также частотой 25 и 75 гц (в системах автоматической блокировки, например, в рельсовых цепях (См. Рельсовая цепь)). В авиационной энергетике используют ток частотой 400 гц (в автономных системах энергопитания). В промышленных и с.-х. установках в некоторых случаях повышают рабочую частоту до 200—400 гц.Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
Смотреть что такое "Частота электрического тока" в других словарях:
dic.academic.ru Угловая частота ω в записанном выражении для мгновенного значения напряжения определяется в зависимости от заданной частоты источника переменного токаω = 2πf = 2 ∙ 3,14 ∙ 50 = 314 1/с . Индуктивные сопротивления xL1 = ω L1 = 314 ∙ 63,8 ∙ 10–3 = 20 Ом, xL2 = ω L2 = 314 ∙ 47,8 ∙ 10–3 = 15 Ом, xL3 = ω L3 = 314 ∙ 63,7 ∙ 10–3 = 20 Ом. Ёмкостные сопротивления xС2 =1/(ω С2) = 1/(314 ∙ 318 ∙ 10–6) = 10 Ом, xС3 =1/(ω С3) = 1/(314 ∙ 212,3 ∙ 10–6) = 15 Ом. Полное сопротивление участков цепи в комплексной форме
Преобразованная цепь изображена на рисунке 6, a. Чтобы не загромождать рисунок, в преобразованной схеме исключены измерительные приборы, которые на расчёт токов и напряжений не влияют. По аналогии с цепью постоянного тока осуществляем эквивалентные преобразования цепи, представленные на рисунках 6, би в.
Параллельно соединенные элементы z2, z3, z4 заменяем одним эквивалентным z234
Последовательно соединенные элементы z1 и z234 заменяем одним эквивалентным
2. Для упрощенной схемы, представленной на рисунке 6, в, по закону Ома определим действующее значение комплексного тока I1 в неразветвленной части цепи
Далее определяем падение напряжения на участках:
Комплексное падение напряжения на параллельном участке:
Токи в ветвях после разветвления:
Если разветвленный участок имеет только две ветви, включенные параллельно, то токи в ветвях после разветвления можно определять без расчета Ucd,используя формулу разброса. 3. Модули показательной формы выражений для токов есть действующие значения реальных токов ветвей, которые фиксируют приборы электромагнитной системы. Следовательно, амперметр в первой ветви покажет 6,764 А. Вольтметр, включенный параллельно емкостному элементу, покажет падение напряжения на нем. Так как падение напряжения на участке есть произведение тока участка на значение его сопротивления, то получаем: , где zV– полное комплексное сопротивление участка, на котором определяется падение напряжения. Так как в примере находим падение напряжения на емкостном элементе с сопротивлением xС3, то
Падение напряжения на емкостном элементе
Показание вольтметра есть модуль выражения UV, т. е.UV= 51,97 В. Ваттметр, включенный на входе цепи, показывает активную мощность, потребляемую всей схемой. Эта мощность будет действительной частью выражения комплекса полной мощности Sна входе, которае имеет вид
Активная мощность Рист = 956,34 Вт, реактивная мощность Qист = 1140,04 вар, значит показание ваттметра Рw = 956,34 Вт 4. Для проверки результатов расчета необходимо составить баланс активных и реактивных мощностей. Эти балансы показывают, что активные и реактивные мощности на входе должны быть равны сумме соответственно активных и реактивных мощностей всех потребителей. Активная мощность на входе определена, а активные мощности отдельных потребителей рассчитывают как произведение активного сопротивления участка на квадрат действующего значения тока этого участка. В рассматриваемой схеме два активных потребителя r1 иr2. Суммарная активная мощность нагрузки
Относительная ошибка вычислений для активной мощности
Ошибка менее одного процента допускается. Она возникает из-за округ- ления числовых данных при расчете. Реактивную мощность потребителей определяют как произведение квадрата тока реактивного элемента на его сопротивление. Причем реактивная мощность катушки индуктивности положительна, а конденсатора отрицательна. studfiles.net Период и частота переменного токаВремя, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период - время одного колебания; Аплитуда - его наибольшее мгновенное значение. Период выражают в секундах и обозначают буквой Т. Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды. 1 мс =0,001сек =10-3сек. 1 мкс=0,001 мс = 0,000001сек =10-6сек. 1000 мкс = 1 мс. Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока. Частота обозначается буквой f и выражается в периодах в секунду или в герцах. Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц. 1000 Гц = 103 Гц = 1 кГц; 1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц; 1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц; Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая. Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен: Т = 1/f = 1/50 = 0,02 сек. И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна: f = 1/T=1/0,02 = 100/2 = 50 Гц Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц. Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты. Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше. Амплитуда переменного тока Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1). infopedia.su Какова частота напряжения тока, а точнее частота электрического тока.
Тема: какая у электрического тока частота, что это (частота напряжения тока).
Выражение "напряжение тока" не верно по своему смыслу. Напряжение и ток, это две различные электрические характеристики. Если хотеть понять, какова частота у электрического тока, то стоит сначала разобраться с самим понятием этого тока. Потом уже стане ясно, что есть сила тока, его частота, напряжение. Итак, давайте сравним электричество с обычной водой. Вода течёт по трубам. Трубы бывают различной толщины. Когда краник в рукомойнике закрытый, то внутри труб имеется определённое давление воды, чем больше его отрываешь, тем больше поток воды начинает течь.
Так вот, воду мы будем сравнивать с самими электрическими частицами (электроны и ионы), их движение по электрическому проводнику будет схоже с движением воды в водопроводной трубе. Давление воды, имеющееся внутри труб будет в некотором смысле уподобляться электрическому напряжению. Ну, а о частоте напряжения тока чуть позже. Итак, у нас имеется электрический источник в виде обычной батарейки, у которой имеется плюс и минус. Если мы к ней подключим, допустим, обычную лампочки или моторчик, используя соединительные проводки, а ещё между ними поставим выключатель, то получится обычная электрическая цепь.
Когда мы замкнём выключатель заряженные частицы из одного полюса батарейки устремятся по проводам к противоположному её полюсу, преодолевая свой путь через провода, лампочку и выключатель. Это движение по создавшейся электрической цепи и есть электрический ток (то есть поток самих заряженных частиц). Когда мы разомкнём выключатель, то ток внутри проводников прервётся, а вместо него появиться (точнее говоря возрастёт) напряжение. Это как в кране с водой. Когда мы закрываем кран, то давление воды внутри труб возрастает.
Если же мы начнём постоянно то замыкать, то размыкать выключатель, мы получим периодическое течение электрического тока в цепи. Так вот, тут мы и можем обнаружить нашу частоту напряжения тока, точнее частоту электрического тока. Из физики известно, что частота измеряется в герцах. Один герц равен 1 колебанию в секунду. Следовательно, если у нас получиться за одну секунду замкнуть и разомкнуть нашу электрическую цепочку 3 раза в секунду, мы получим частоту электрического тока (не правильно выражаясь - частоту напряжения тока) в 3 герца. Ну думаю смысл понятен.
Теперь, где мы можем обнаружить эту самую частоту электрического тока. Думаю все слышали, что в обычной домашней розетки напряжение равно 220 вольтам, а частота этого тока (переменного) 50 герц. Это стандартная частота для обычной бытовой электрической сети 220 и 380 вольт. Она зависит от определённых параметров и характеристик, используемых в электроснабжении города. В других электрических и электронных устройствах и системах может применяться другая частота. К примеру, в обычных домашних компьютерах используется частота уже измеряемая в мегагерцах (средняя частота компьютерного процессора равна около 2.7 мегагерца, это довольно высокая частота электрического тока).
Если мы в примере с батарейкой просто замыкали и размыкали переключатель в цепи, получая при этом просто прерывистое течение тока, то в случае переменного тока всё иначе. Переменный ток имеет синусоидальную форму, периодически изменяя свою полярность. То есть, за свои 50 герц в секунду переменный ток в сети попеременно 25 раз плавно будет нарастать то в одной части графика (график зависимости напряжения, тока от времени) (на двух имеющихся проводах будет одна полярность), то 25 раз в противоположной части (другая полярность, + меняется на -, а - на +).
P.S. Из примеров выше думаю Вы поняли, что же такое частота электрического тока (частота напряжения тока, выражаясь неправильно). Это всего лишь периодичность колебаний движения электрических заряженных частиц, движущихся в проводнике. То есть, грубо выражаясь, скорость изменения состояния покоя-движения этих самых частиц (электронов). electrohobby.ru Электротехника: Резонансная частота.Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты.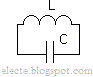 Рисунок 1 - Параллельный колебательный контур Рисунок 1 - Параллельный колебательный контур 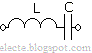 Рисунок 2 - Последовательный колебательный контур Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле: Где L-индуктивность катушки контура, C-ёмкость конденсатора контура. Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют - резонансом токов, резонанс в последовательном контуре - резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны: Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:electe.blogspot.com Электрический ток и его частотаОсновные понятия и определения электротехникиОдним из основных понятий электротехники является понятие об электрическом токе. Электрический ток — это направленное движение электрических зарядов в веществе или вакууме под воздействием электромагнитного поля. Ток характеризуется силой, измеряемой в амперах (А). Один ампер соответствует перемещению через поперечное сечение проводника в течение одной секунды (с) заряда электричества величиной в один кулон (Кл): 1А = 1 —. В общем случае, обозначив ток буквой /, а заряд q, получим dt Следует отметить, что существует ряд других определений электрического тока, среди которых особое место занимает до сих пор не вполне осмысленное определение Майкла Фарадея (в современной интерпретации): электрический ток есть ось сил, в направлении которых действует электромагнитное поле. По типу носителей электрических зарядов и среды их перемещения различают токи проводимости, смещения и переноса. Проводимость делят на электронную и ионную. Для установившихся режимов различают два вида токов: постоянный и переменный. Постоянным называют ток, который может изменяться по величине, но не изменяет своего знака сколь угодно долгое время. Переменным называют ток, который периодически изменяется как по величине, так и по знаку. Переменные токи подразделяют на синусоидальные и несинусоидальные. Синусоидальным называют ток, изменяющийся по гармоническому закону: i = Imsm(ot, где Iw — амплитудное (наибольшее) значение тока, А, Скорость изменения переменного тока характеризуется его частотой, определяемой как число полных повторяющихся колебаний в единицу времени. Частота обозначается буквой / и измеряется в герцах (Гц).Так, частота тока в сети 50 Гц соответствует 50 полным колебаниям в секунду. Угловая частота 0) — скорость изменения тока в радианах в секунду и связана с частотой простым соотношением: со = 2л/. Установившиеся (фиксированные) значения постоянного и переменного токов обозначают прописной буквой I, неустановившиеся (мгновенные) значения — строчной буквой /. Условно положительным направлением тока считают направление движения положительных зарядов. www.proelectro2.ru |
|
||||||||||||||||||
|
|
||||||||||||||||||
|







 .
.