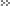Расчет потерь мощности в трансформаторах. Потери в трансформаторе формулаКак посчитать потери мощности и электроэнергии? Еще не изобрели и вряд ли изобретут способы передачи электроэнергии без потерь. В каждой линии, в каждом элементе системы электроснабжения происходят потери энергии. Потери мощности и энергии составляют около 12-15% от вырабатываемой электроэнергии. Потери электроэнергии покрываются за счет увеличения мощности источников питания, а это значит за счет увеличения энергоресурсов. В наше время цены на энергоресурсы постоянно растут, поэтому вопрос энергосбережения очень актуален. При проектировании нужно понимать, где происходят основные потери электроэнергии и принимать все необходимые меры к снижению данного показателя. Рассмотрим случай электроснабжения объекта от трансформаторной подстанции. Большинство объектов подключено именно таким способом, т.е. от ТП 10/0,4кВ или от ТП 6/0,4кВ. Основными элементами, где происходят потери, является трансформатор и ЛЭП (КЛ или ВЛ). Методика расчета потерь мощности и энергии:1 Определение потерь мощности в трансформаторе. Потери активной мощности в трансформаторах (в кВт) определяются по следующей формуле: ∆Pт=∆Pст+∆Pм·β2 где ∆Pст=∆Pх – потери холостого хода трансформатора при номинальном напряжении, кВт; ∆Pм=∆Pк – потери короткого замыкания трансформатора при номинальной нагрузке, кВт; β=S/Sном,т – коэффициент загрузки трансформатора. Потери реактивной мощности в трансформаторе (в квар) определяются выражением: ∆Qт=∆Qх+∆Qк·β2 где ∆Qх – потери на намагничивание; ∆Qк – потери, обусловленные потоками рассеяния.  Потери реактивной мощности в трансформаторе где uк – напряжение короткого замыкания трансформатора, %; Iх – ток холостого хода трансформатора, %; хт – индуктивное сопротивление трансформатора, Ом. 2 Определение потерь мощности в ЛЭП. Потери активной мощности в трехфазной линии (в кВт) с равномерной загрузкой фаз определяются по следующей формуле: ∆Рл=3·I2max·rл·10-3 Потери реактивной мощности (в квар): ∆Qл=3·I2max·хл·10-3 Потери мощности в линии можно выразить в процентах от расчетной мощности: ∆Р’л=∆Рл·100/Рmax Если реактивная составляющая потери напряжения мала и ей можно пренебречь, то потери мощности в линии можно найти через потери напряжения: ∆Р’л=∆U/cos2ϕ При расчете потерь энергии используют такое понятие как время наибольших потерь τ. Время наибольших потерь – это условное время, в течение которого при передаче электроэнергии с максимальной нагрузкой, потери энергии были бы такими, какие возникают в действительности при переменном графике нагрузки. Время наибольших потерь определяют из кривых зависимости этого времени от годовой продолжительности использования максимума нагрузки.  Время наибольших потерь 3 Определение годовых потерь энергии в трансформаторе. Годовые потери активной энергии в трансформаторе, кВт·ч: ∆Wат=∆Pст·t+∆Pм·β2·τ где t – время работы трансформатора. Годовые потери реактивной энергии в трансформаторе, квар·ч: ∆Wрт=Ix·Sномт·t/100+uк·Sномт·β2·τ/100 4 Определение годовых потерь энергии в ЛЭП. Годовые потери активной энергии в линии, кВт·ч: ∆Wал=3·I2max·rл·τ·10-3 Годовые потери реактивной энергии в линии, квар·ч: ∆Wрл=3·I2max·хл·τ·10-3 Про годовую продолжительность использования максимума нагрузки будет написана отдельная статья.Программа для расчета потери мощности и электроэнергии. Советую почитать:220blog.ru Расчет потерь мощности в трансформаторахПоиск Лекций
Потери активной мощности в трансформаторах определяются по формуле [1], кВт:
реактивной, квар, –
где
Результаты расчета необходимо представить в виде табл. 6. Таблица 6 Результаты расчета потерь активной и реактивной мощности в трансформаторах
4. ЭЛЕКТРИЧЕСКИЙ РАСЧЕТ СЕТИ НАПРЯЖЕНИЕМ 10 кВ
Электрический расчет схемы одностороннего питания сети Напряжением 10 кВ
Одиночная магистраль, питаемая с одной стороны, проста по конструктивному исполнению, но не обеспечивает высокой надежности электроснабжения, поскольку любое повреждение отражается на питании всех приемников, присоединенных к ней. Разомкнутые сети применяют по следующим причинам. Во-первых, в разомкнутых схемах почти в два раза ниже токи короткого замыкания, чем в замкнутых. Это позволяет применять дешевую коммутационную аппаратуру, устанавливаемую в цепях напряжением 6 и 10 кВ. Во-вторых, для обеспечения селективности релейной защиты потребуется дорогая и сложная аппаратура, вследствие малых индуктивных сопротивлений кабельных линий, широко применяемых в этих сетях. Экономические и технические преимущества, достигаемые при использовании простой и дешевой коммутационной аппаратуры и релейной защиты, превосходят ущерб, определяемый особенностями разомкнутых распределительных сетей. В соответствии с ПУЭ [4] питание подстанций, предназначенных для электроснабжения электроприемников первой категории, должно осуществляться при одностороннем питании по двухцепной ЛЭП. Электрический расчет схемы одностороннего питания сети напряжением 10 кВ начинают с составления расчетной схемы в соответствии с рис. 5. Расчетную схему необходимо привести в пояснительной записке на листе формата А4 в масштабе.
Рис. 5. Расчетная схема одностороннего питания сети 10 кВ
На расчетной схеме кроме длины участков указывают суммарные мощности SΣ1 – SΣ3 от нагрузок подстанций SТП1 – SТП3 с учетом потерь мощности ∆SТП1 – ∆SТП3, передаваемые по участкам l1 – l3. Суммарная активная мощность, передаваемая по i-му участку сети, определяется по формуле: SΣi = PΣi + j QΣi, (15)
где PΣi и QΣi – суммарные активная и реактивная мощности, протекающие по i-му участку. Например, для участка длиной l1 суммарную передаваемую активную и реактивную мощности можно определить по формулам:
PΣ1= PТП1+ PТП2 + PТП3 + ΔPтр1 + ΔPтр2 + ΔPтр3; (16)
QΣ1= QТП1+ QТП2 + QТП3 + ΔQтр1 + ΔQтр2 + ΔQтр3. (17)
Аналогично определяются суммарные активные PΣ2, PΣ3 и реактивные QΣ2, QΣ3 мощности. Величины ΔPтр1 – ΔPтр3 и ΔQтр1 – ΔQтр3 рассчитаны в подразд. 3.2, PТП1 и PТП2 заданы в исходных данных (см. табл. 1), PТП3 рассчитана в разд. 3. По аналогии с формулой (15) определяются нагрузки подстанций SТП1 – SТП3 и потери мощности ΔSТП1 – ΔSТП3 в трансформаторах подстанции:
SТПi = PТПi + j QТПi; (18)
ΔSТПi = DPтрi + j DQтрi. (19)
Зная суммарную мощность и номинальное напряжение сети, принимаемое равным 10 кВ, определяются токи I1 – I3, протекающие по участкам, по формуле, А:
При проектировании воздушных линий напряжением до 500 кВ включительно выбор сечения провода производится по нормированным обобщенным показателям. В качестве таких показателей используются нормированные значения экономической плотности тока. Введем понятие «экономическое сечение провода» Fэк – это сечение, при котором приведенные затраты на линию будут наименьшими. Плотность тока, соответствующая экономическому сечению, называется экономической плотностью тока jэк. Данная плотность тока не зависит от нагрузки, а определяется только типом проводов (изолированные, неизолированные), материалом, районом проложения линии и временем использования максимума активной мощности Тmax. Время использования максимума нагрузки – это условное время, в течение которого линия, работая с максимальной нагрузкой Imax, передала бы такое же количество энергии, что и при работе по действительному графику I(t) за год. Значения плотности тока для воздушных линий, нормированные в соответствии с правилами [4], приведены в табл. 7. Таблица 7 Нормированные значения плотности тока для воздушных линий
Экономическая площадь сечения провода определяется по формуле, мм2:
где Iэкв – эквивалентный расчетный ток, А. Эквивалентный расчетный ток – это неизменный по длине линии ток, который вызывает в ней те же потери, что и все действительные токи на отдельных участках. Как видно из определения – это условное понятие, которое используется в случае, если в сети, различные участки которой можно выполнить проводами разного сечения, используют провода одного сечения. Эквивалентный расчетный ток находят по формуле, А:
Рассчитывается экономическая площадь сечения провода для схемы одностороннего питания и округляется до ближайшего стандартного значения. При выполнении курсовой работы на основании расчета рекомендуется выбрать алюминиевые или сталеалюминиевые провода из справочных материалов [2, 3], каталогов или прил. 1 и привести их параметры в расчетно-пояснительной записке. Далее необходимо проверить выбранные провода по допустимой потере и отклонению напряжения. По нагреву выполнять проверку не обязательно, так как нормированная экономическая плотность тока значительно ниже плотности тока, допустимой по нагреванию (для алюминия jнагр = 4 А/мм2, для меди jнагр = 7 А/мм2 ). Сечение провода проектируемой воздушной линии должно обеспечивать выполнение следующего условия (см. рис. 5): потери напряжения от пункта питания (в данном случае ГПП) до наиболее удаленных приемников (ТП3) в различных режимах не должны быть больше допустимого значения. Для сетей напряжением 10 кВ допустимые потери напряжения в нормальном режиме рекомендуется принимать 8 % от номинального (800 В), а в аварийном – 12 % (1200 В). Расчет необходимо произвести для двух режимов: нормального, когда в работе находятся обе цепи ЛЭП, и аварийного, когда в работе находится одна ЛЭП. При выполнении данного расчета следует обратить внимание на то, что сопротивление линии в нормальном режиме в два раза меньше, чем в аварийном. Потери напряжения до наиболее удаленной точки сети определяются как сумма потерь напряжения на всех участках, В:
где
Потери напряжения до наиболее удаленной точки сети, полученные по формуле (23), сравнивают с допустимыми:
ΔU ≤ ΔUдоп. (25)
Если условие (25) не выполняется для какого-либо из режимов, то необходимо увеличить сечение провода и проверку повторить. В связи с тем, что режим работы сетей, а также их нагрузок, постоянно меняется, – меняется и напряжение у приемников электроэнергии. Плавные длительные изменения называют установившимся отклонением напряжения. Эту величину определяют как разность между напряжением на зажимах электроприемников и их номинальным напряжением [5], %:
В соответствии с ГОСТ 13109-97 [5] принимаются следующие допустимые отклонения напряжения на шинах наиболее удаленного потребителя: для нормального режима – Отклонение напряжения на шинах наиболее удаленной подстанции (ТП3) рассчитывают для двух режимов: для максимальной и минимальной нагрузки. Для этого необходимо по заданному отклонению напряжения найти напряжение на шинах ГПП для обоих режимов по формулам, кВ:
где kmax и kmin – максимальное и минимальное заданные в исходных данных отклонения напряжения на шинах ГПП в относительных единицах (см. табл. 1). Напряжение на шинах наиболее удаленной подстанции в обоих режимах определяется по формуле, кВ:
Отклонение напряжения на шинах наиболее удаленного потребителя, полученное по формуле (26), сравнивают с допустимым:
δUmax(min) ≤ δUдоп. (30) Если условие (30) не выполняется для какого-либо из режимов, то необходимо увеличить сечение провода и проверку повторить.
poisk-ru.ru Определение потерь и кпд трансформатораПотери активной мощности в трансформаторе подразделяются на электрические потери в обмотках и магнитные потери в магннто- проводе. Добавочные потери на вихревые токи в обмотках (см. § 12-3) включаются в электрические потерн. Кроме того, возникают потери на вихревые токи от полей рассеяния также в стенках бака и в кре¬пежных деталях. Так как эти потери пропорциональны квадрату тока, то они тоже относятся к электрическим потерям. Опытное значение активного сопротивления короткого замыкания гк учиты¬вает и эти добавочные потери. Значение потерь определяется расчетным путем при проектиро¬вании трансформатора или опытным путем в готовом трансфор¬маторе. Согласно ГОСТ 11677—75, магнитные потерн рш. определяются из опыта холостого хода (см. § 14-5). Как было установлено в § 15-1, поток трансформатора при l/j = = const с изменением нагрузки несколько изменяется, в соответ¬ствии с чем изменяются также магнитные потери. Однако это изме¬нение относительно невелико, и поэтому при иг — Ula = const магнитные потери при всех нагрузках принимаются, согласно ГОСТ 11677—75, равными мощности холостого хода Р0 при этом напря¬жении. Электрические потери рэл, включая добавочные, при номиналь¬ном токе принимаются равными мощности короткого замыкания Рк при этом же токе (см. § 14-5). Обычно в опыте короткого замыкания температура обмоток # отличается от 75° С, и поэтому мощность Рк приводится к 75° С, для чего опытное значение потерь множится при медных обмотках на коэффициент Коэффициент полезного действия определяется отношением мощности , отдаваемой трансформатором в нагрузку, к мощности, потребляемой из сети: . Коэффициент полезного действия характеризует эффективность преобразования напряжения в трансформаторе. При практических расчетах вычисляют по формуле , (2.20) где - полные потери в трансформаторе. Формула (2.20) менее чувствительна к погрешностям в определении ии поэтому позволяет получить более точное значение. Полезная мощность вычисляется по формуле , (2.21) где - коэффициент нагрузки трансформатора. Электрические потери в обмотках определяются из опыта короткого замыкания , (2.22) где - потери короткого замыкания при номинальном токе. Потери в стали определяются из опыта холостого хода . (2.23) Они принимаются постоянными для всех рабочих режимов работы трансформатора, так как при ЭДСв рабочих режимах меняется незначительно. Подставляя соотношения (2.21)(2.23) в формулу (2.20), получим . (2.24) Анализ этого выражения показывает, что имеет максимальное значение при нагрузке, когда потери в обмотках равны потерям в стали, . Отсюда получаем оптимальное значение коэффициента нагрузки .
В современных силовых трансформаторах отношение потерь , поэтому максимум имеет место при (рис.2.21). Из кривой видно, чтотрансформатор имеет практически постоянный коэффициент полезного действия в широком диапазоне изменения нагрузки от 0,5 до 1,0. При малых нагрузках трансформатора резкого снижается.
На трансформаторных подстанциях обычно устанавливается несколько параллельно работающих трансформаторов. Это обусловлено следующими причинами:
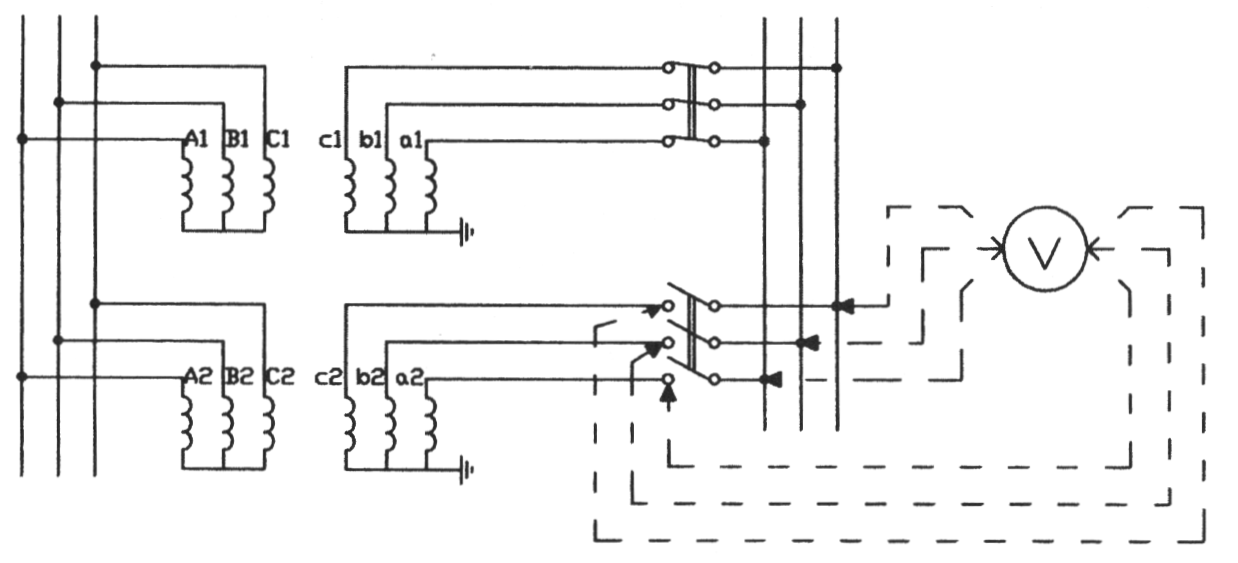
Параллельное включение трехфазных трансформаторов осуществляется по схеме, приведенной на рис. 2.29. При параллельной работе трансформаторов возникает проблема обеспечения равномерного распределения нагрузки между ними. Равномерность распределения нагрузки обеспечивается в том случае, если трансформаторы имеют
Если первые два условия соблюдены, то вторичные ЭДС параллельно включенных трансформаторов будут равны по величине и по фазе и поэтому будут уравновешивать друг друга. В противном случае уже на холостом ходу возникает уравнительный ток . Этот ток, складываясь с током нагрузки, вызывает неравномерное распределение нагрузки, а также дополнительные потери и нагрев трансформаторов. При большой разнице ЭДС токможет быть опасным для трансформаторов. Соблюдение третьего условия обеспечивает равномерное распределение токов между трансформаторами при нагрузке. Анализ особенностей параллельной работы двух трансформаторов можно выполнить с помощью упрощенной схемы замещения (рис. 2.30). Трансформаторы в этой схеме представлены внутренними сопротивлениями и. В цепь второго трансформатора включен источник ЭДС, учитывающий несоблюдение первых двух условий параллельной работы трансформаторов,
. Если , то ток нагрузкираспределяется между трансформаторами обратно пропорционально их внутренним сопротивлениям: ; . Если , то в замкнутом контуре, образованном сопротивлениямии, потечет уравнительный ток , вызывая неравномерное распределение тока нагрузки между трансформаторами: ; .
Ввиду малого внутреннего сопротивления трансформатора уровень тока может быть весьма значительным. Например, при включении на параллельную работу трансформаторов с группами соединений обмотокY/Y-0 и Y/-11 вторичные ЭДС будут сдвинуты по отношению друг к другу на 30 (рис. 2.31). Принимая модули приведенных значений ЭДС иодинаковыми и равными 1о.е., найдем из рис. 2.31 модуль ЭДС При модуль уравнительного тока, вызванного этой ЭДС, превысит пятикратное значение , что недопустимо. Поэтому на параллельную работу включаются трансформаторы только с одинаковыми группами соединений обмоток. Если трансформаторы имеют разные коэффициенты трансформации, то величина ЭДС может быть приближенно вычислена по выражению .
Примем для определенности , тогда ЭДСбудет находиться в противофазе с напряжением. Примодуль уравнительного тока, вызванного этой ЭДС, составит , а его фаза будет определяться аргументами комплексных сопротивлений и. Появление уравнительного тока приведет к уменьшению нагрузки первого трансформатора и ее увеличению у второго (рис. 2.32). Для того, чтобы не вызвать серьезного нарушения параллельной работы трансформаторов, различие в коэффициентах трансформации не должно превышать 0,5%. При равенстве коэффициентов трансформации, и ток нагрузки будет распределяться обратно пропорционально сопротивлениям: . В общем случае эти токи не совпадают по фазе. Однако фазовый сдвиг незначителен и его можно не учитывать, тогда . (2.26) Выразим сопротивления короткого замыкания через их значения в относительных единицах: ; . Подставим эти выражения в формулу (2.26): . Так как напряжения параллельно работающих трансформаторов одинаковы, отношения токов можно заменить отношением мощностей: . Если , то трансформаторы будут нагружаться пропорционально их номинальным мощностям. Очевидно, что при этом условия параллельной работы являются наилучшими. Если жене равны, то сильнее будет нагружаться тот трансформатор, у которогоменьше. Допускается включать на параллельную работу трансформаторы, у которыхотличается от среднеарифметического не более чем на10%. studfiles.net Потери электроэнергии в трансформаторахПотери электроэнергии в трансформаторах – один из видов технических потерь электроэнергии, обусловленных особенностями физических процессов, происходящих при передаче энергии. Передача электрической энергии от источника к конечному потребителю неизбежным образом связана с потерей части мощности и энергии в системе электроснабжения. Сюда относятся потери в линиях электропередач и потери электроэнергии в трансформаторах. Устройство стандартного двухобмоточного трансформатора включает замкнутый сердечник (магнитопровод), представляющий собой набор пластин из трансформаторной стали, и две обмотки: к генератору (первичная) и к нагрузке (вторичная). Эффект трансформации при этом возникает из-за разного количества витков в обмотках. Потери электроэнергии в трансформаторе такой конфигурации складываются из: потерь на нагревание обмоток трансформатора; потерь на нагревание сердечника; потери на перемагничивание сердечника. Величина потерь электроэнергии в трансформаторе зависит, главным образом, от качества, конструкции и материала трансформаторной стали, из которой изготовлен сердечник. Потери электроэнергии намного больше в случае, если сердечник имеет монолитную конструкцию, поэтому на практике сегодня монолитные сердечники не применяются. Для дополнительной изоляции друг от друга пластины сердечника лакируются. Величина указанных потерь и КПД работы трансформатора определяется также величиной передаваемого напряжения и мощностью. Чем больше мощность трансформатора, тем выше КПД и ниже уровень потерь. При правильной конструкции коэффициент полезного действия трансформатора составляет 97-99%. Потери электроэнергии в трансформаторах определяются также длительностью их работы, поэтому одним из ключевых условий, обеспечивающих снижение потерь электроэнергии в трансформаторах, является отключение их при малых загрузках. Это возможно осуществить, если в ночное время, а также в выходные и праздничные дни питать работающие электроустановки, количество которых не особо велико, от одного трансформатора. Данная возможность обеспечивается наличием перемычек между подстанциями на низшем напряжении. Еще одним немаловажным условием снижения потерь электроэнергии в трансформаторах является обеспечение рационального режима работы включенных трансформаторов. Для этих целей важно выбрать оптимальный коэффициент загрузки трансформатора, зависящий от уровня активных и реактивных составляющих потерь. Для точного подсчета потерь электроэнергии в трансформаторе с двумя обмотками необходимы следующие данные: паспортные: номинальная мощность трансформатора, потери холостого хода при номинальном напряжении и потери короткого замыкания трансформатора при номинальной нагрузке; фактические: полное число часов работы трансформатора, число часов работы трансформатора с номинальной нагрузкой, энергия, учтенная по счетчикам. По этим исходным данным определяются: средневзвешенный коэффициент мощности трансформатора; коэффициент нагрузки трансформатора; и, собственно, потери электроэнергии в трансформаторе, в киловатт-часах. Для расчета потерь электроэнергии в трансформаторе с тремя обмотками выделяются коэффициенты нагрузки для каждой из обмоток – высшего, среднего и низшего напряжений, и общие потери электрической энергии рассчитываются как средневзвешенная величина с учетом данных показателей. Умение правильно рассчитать потери во всех звеньях системы электроснабжения, выявить их ключевые составляющие и установить приоритетные направления по снижению потерь и экономии электроэнергии — основное условие правильной эксплуатации электрической сети, в частности, снижения потерь электроэнергии в трансформаторах. Метки: потери электроэнергии, потери электроэнергии в трансформаторах, современная электроэнергетика, трансформатор, электросети, энергоснабжение Интересная статья? Поделитесь ей с друзьями: novostienergetiki.ru Потери в трансформаторе — МегаЛекцииВ работающем трансформаторе всегда имеются как магнитные, так и электрические потери. Магнитные потери в трансформаторе слагаются из потерь на вихревые токи и гистерезис: Величина этих потерь зависит от напряжения U1 и магнитной индукции В. Можно считать, что при U1 = const, рон= В2. Они не зависят от нагрузки, то есть являются постоянными. Электрические потери в обмотках, наоборот, переменные, то есть: где ркн — соответствует потерям при коротком замыкании трансформатора. Если известны потери короткого замыкания при номинальной нагрузке, то электрические потери в трансформаторе можно определить по формуле: где β — коэффициент загрузки трансформатора. Суммарные потери в трансформаторе: _____________________________________________________________________________ 9. Определяют в лаб. работе коэффициент нагрузки bмакс, соответствующий максимальному значению кпд трансформатора
bмакс = . Определение потерь мощности. Согласно требованиям ГОСТа потери мощности в трансформаторе определяют по данным опытов холостого хода и короткого замыкания. Получаемый при этом результат имеет высокую точность, так как при указанных опытах трансформатор не отдает мощность нагрузке. Следовательно, вся мощность, поступающая в первичную обмотку, расходуется на компенсацию имеющихся в нем потерь.При опыте холостого хода ток I0 невелик и электрическими потерями мощности в первичной обмотке можно пренебречь. В то же время магнитный поток практически равен потоку при нагрузке, так как его величина определяется приложенным к трансформатору напряжением. Магнитные потери в стали пропорциональны квадрату значения магнитного потока. Следовательно, с достаточной точностью можно считать, что магнитные потери в стали магнитопровода равны мощности, потребляемой трансформатором при холостом ходе и номинальном первичном напряжении,т. е. ΔРм ≈ Р0. (2.52) Для определения суммарных электрических потерь согласно упрощенной схеме замещения (см. рис. 2.33,a) полагают, что 1'2 = 11.При этом ΔPэл = ΔPэл1 + ΔPэл2 = I12R1 + I'22R2≈ I'22(R1+ R'2)≈ I'22Rк,(2.53) или
ΔРэл ≈ β2I'22номRк ≈ β2ΔPэл.ном,(2.54) где ΔPэл.ном - суммарные электрические потери при номинальной нагрузке.
За расчетную температуру обмоток — условную температуру, к которой должны быть отнесены потери мощности ΔРэл и напряжение ик,принимают: для масляных и сухих трансформаторов с изоляцией классов нагревостойкости А, Е, В (см. § 12.1) температуру 75°С; для трансформаторов с изоляцией классов нагревостойкости F, Н — температуру 115 °С. ВеличинуΔРэл.ном ≈ I'22номRк ≈I12номRкможно с достаточной степенью точности принять равной мощности Рк, потребляемой трансформатором приопыте короткого замыкания, который проводится при номинальном токе нагрузки. При этом магнитные потери в стали ΔРмвесьма малы по сравнению с потерями ΔPэл из-за сильного уменьшения напряжения U1,a следовательно, и магнитного потока трансформатора и ими можно пренебречь. Таким образом, ΔРэл = β2Pк(2.55) Полные потери ΔP=Po + β2Pк (2.56) Подставляя полученные значения Рв (2.51) и учитывая, что Р2= U2I2cosφ2 ≈ βSномcosφ2, находим
Эта формула рекомендуется ГОСТом для определения КПД трансформатора. Значения Ро и Рк для силовых трансформаторов приведены в соответствующих стандартах и каталогах. Зависимость КПД от нагрузки. По (2.57) можно построить зависимость КПД от нагрузки (рис. 2.39, а). При β = 0 полезная мощность и КПД равны нулю. С увеличением отдаваемой мощности КПД увеличивается, так как в энергетическом балансе уменьшается удельное значение магнитных потерь в стали, имеющих постоянное значение. При некотором значении βопт кривая КПД достигает максимума, после чего начинает уменьшаться с увеличением нагрузки. Причиной этого является сильное увеличение электрических потерь в обмотках, возрастающих пропорционально квадрату тока, т. е. пропорционально β2, в то время как полезная мощность Р2возрастает только пропорционально β. Максимальное значение КПД в трансформаторах большой мощности достигает весьма высоких пределов (0,98—0,99). Оптимальный коэффициент нагрузки βопт, при котором КПД имеет максимальное значение, можно определить, взяв первую производную dη/dβ по формуле (2.57) и приравняв ее нулю. При этом
Следовательно, КПД имеет максимум при такой нагрузке, при которой электрические потери в обмотках равны магнит ным потерям в стали.
Читайте также: megalektsii.ru |
|
|||||||||||||||||
|
|
|||||||||||||||||
|




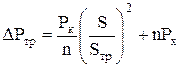 ; (13)
; (13)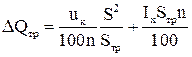 , (14)
, (14)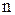 – количество установленных трансформаторов;
– количество установленных трансформаторов;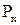 и
и 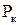 – потери холостого хода и короткого замыкания, кВт;
– потери холостого хода и короткого замыкания, кВт;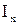 – ток холостого хода, %;
– ток холостого хода, %;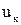 – напряжение короткого замыкания, %;
– напряжение короткого замыкания, %;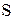 – мощность нагрузки трансформаторной подстанции, кВ·А;
– мощность нагрузки трансформаторной подстанции, кВ·А;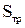 – номинальная мощность трансформатора, кВ·А.
– номинальная мощность трансформатора, кВ·А.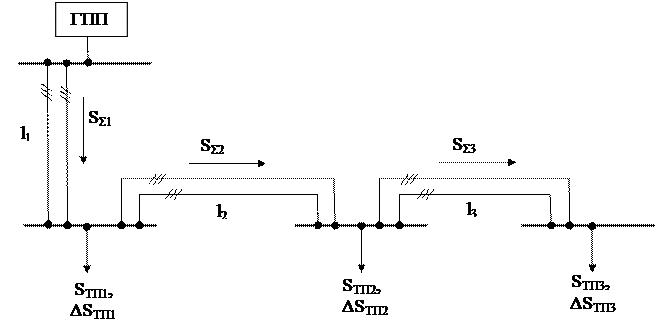
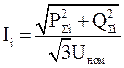 . (20)
. (20)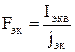 , (21)
, (21)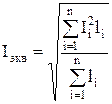 . (22)
. (22)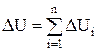 , (23)
, (23)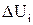 – потери напряжения на i-м участке, В,
– потери напряжения на i-м участке, В,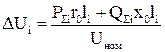 . (24)
. (24)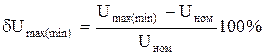 . (26)
. (26)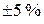 , для остальных режимов –
, для остальных режимов – 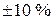 .
.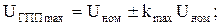 (27)
(27)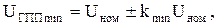 (28)
(28)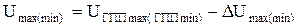 . (29)
. (29)