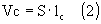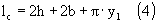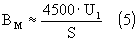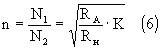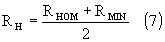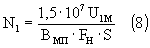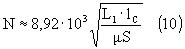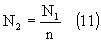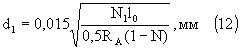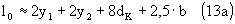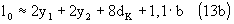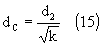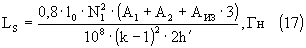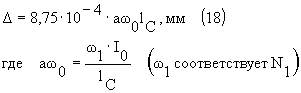51. Взаимная индукция. Трансформаторы. Коэффициент трансформации. Индукция трансформатораИндуктивности обмоток трансформатора и электромагнитное рассеяниеИндуктивности обмотокВ трансформаторах со стальным магнитопроводом магнитная проницаемость стали µ во время цикла перемагничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные L и взаимные М индуктивности обмоток трансформатора. В результате такого непостоянства µ при подключении трансформатора к сети с синусоидальным напряжем в его намагничивающем токе i0 возникают высшие гармоники (смотрите статью "Явления, возникающие при намагничивании магнитопроводов трансформаторов").
При работе трансформатора на ток i0 накладывается ток нагрузки, по отношению к которому ток i0 и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока i0. Это равносильно допущению, что во время цикла перемагничивания µ, L и M постоянны. Влияние насыщения магнитопровода при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока магнитопровода, значения µ, L и M для данного режима работы. В соответствии с изложенным будем полагать, что µ, L и M постоянны. Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком магнитопровода Фс, все силовые линии которого полностью замыкаются по замкнутому магнитопроводу и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рисунок 1). Пусть поток Фс создается током первичной обмотки i1, когда ток вторичной обмотки i2 = 0. Значения Фс и i1 могут быть известны, например, из данных расчета магнитной цепи или из опыта. Тогда собственная индуктивность первичной обмотки от потока в магнитопроводе
Величину Lс1 можно выразить также через магнитное сопротивление магнитопровода
где lk, Sk и µk соответственно означают длину, площадь сечения и магнитную проницаемость k-го участка магнитной цепи. При этом
и после подстановки этого значения Фс в выражение (1) получим Отметим, что значение Rµc также может быть определено по данным расчета магнитной цепи или из данных опыта по соотношению (3). Аналогично индуктивность вторичной обмотки от потока магнитопровода а взаимная индуктивность первичной и вторичной обмоток от потока магнитопровода
Картина магнитного поля, замыкающегося целиком по магнитопроводу, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление потоку Фс одинаково для поля обеих обмоток и в равенства (4), (5) и (6) входит одинаковая величина Rµс. Вследствие этого также
Кроме потока Фс, ток первичной обмотки i1 создает также поток Фв1 (рисунок 1), силовые линии которого замыкаются частично по воздуху или через трансформаторное масло. Потокосцеплениям Ψв1 и Ψв12 этого потока с первичной и вторичной обмотками соответствует собственная индуктивность первичной обмотки Lв1 = Ψв1 / i1 и взаимная индуктивность двух обмоток Mв12 = Ψв12 / i1. Точно так же при питании вторичной обмотки током i2 создается поток Фв2, замыкающийся частично по воздуху. Потокосцеплениям Ψв2 и Ψв21 этого потока с вторичной и первичной обмотками соответствует собственная индуктивность вторичной обмотки Lв2 = Ψв2 / i2 и взаимная индуктивность двух обмоток Mв21 = Ψв21 / i2. При этом, согласно принципу взаимности, Mв12 = Mв21 = Mв Поля потоков Фв1 и Фв2 имеют гораздо более сложный характер, чем поле потока Фс. Отдельные магнитные линии этих потоков сцепляются с неполными и разными числами витков первичной и вторичной обмоток. Поэтому в отличие от Lс2 [смотрите соотношение (7)]
Полные собственные индуктивности первичной и вторичной обмоток
и полная взаимная индуктивность Первые слагаемые равенств (9) и (10) значительно больше вторых, так как потоки через воздух относительно малы. Понятие об электромагнитном рассеянииПолнота электромагнитной связи двух индуктивно связанных цепей характеризуется коэффициентом связи этих цепей
Как известно из курса теоретических основ электротехники, в реальных условиях всегда c < 1. Если бы в трансформаторе отсутствовали потоки Фв1 и Фв2, замыкающиеся по воздуху, то L11 = Lc1, L22 = Lc2, M = Mc, и в этом случае в соответствии с равенствами (4), (5), (6) и (11)
Таким образом, неполнота электромагнитной связи в трансформаторе, выражаемая неравенством c < 1, обусловлена наличием потоков Фв1 и Фв2 или, точнее, неодинаковым их сцеплением с обеими обмотками. Условие c = 1 было бы достигнуто только в том случае, если бы удалось полностью совместить первичную и вторичную обмотки, что фактически невозможно.Явление неполной электромагнитной связи называется электромагнитным рассеянием. Наряду с соотношением (11) целесообразно ввести в рассмотрение коэффициент электромагнитного рассеяния
Чем меньше c и чем больше σ, тем больше рассеяние. Ввиду того что явление рассеяния обусловлено неодинаковостью или неполнотой сцепления потоков Фв1 и Фв2, проходящих по воздуху, с обеими обмотками, эти потоки называют часто также потоками рассеяния, однако это название до некоторой степени условно, так как потоки Фв1 и Фв2 обусловливают также явление взаимной индукции, поскольку Mв ≠ 0. Степень неполноты электромагнитной связи, или величина электромагнитного рассеяния, оказывает большое влияние на многие технические показатели и характеристики трансформаторов и вращающихся электрических машин. В трансформаторах с ферромагнитным магнитопроводом потоки Фв1 и Фв2 относительно малы. Поэтому электромагнитная связь в трансформаторах чрезвычайно высока, а рассеяние мало. В силовых трансформаторах, например, c = 0,998 – 0,9995 и соответственно σ = 0,001 – 0,004. Вследствие этого значение σ, определяемое по формуле (12), представляет собой разность весьма близких величин и вычисление σ по этой формуле связано с очень большими погрешностями, так как L11, L22 и M в практических устройствах не могут быть рассчитаны или определены из опыта с достаточной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние. Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с. www.electromechanics.ru Индуктивность трансформатораИтак, явление взаимной индукции используется в широко распространенных устройствах – трансформаторах. Трансформатор был изобретен Яблочковым, русским ученым, в 1876 г. для раздельного питания отдельных электрических источников света (свечи Яблочкова). Рассчитаем взаимную индуктивность двух катушек и , намотанных на общий сердечник (рис. 5.5). Когда в первой катушке идет ток , в сердечнике возникает магнитная индукция и магнитный поток Ф через поперечное сечение S.
Рис. 5.5. Магнитное поле тороида можно рассчитать по формуле
Через вторую обмотку проходит полный магнитный поток , сцепленный со второй обмоткой:
здесь – потокосцепление, которое можно найти по формуле:
По определению, взаимная индуктивность двух катушек равна:
К первичной обмотке подключена переменная ЭДС . По закону Ома ток в этой цепи будет определяться алгебраической суммой внешней ЭДС и ЭДС индукции.
где – сопротивление обмотки. – делают малым (медные провода) и . Тогда
Во второй обмотке, по аналогии, , отсюда
Если пренебречь потерями, т.е. предположить, что , то
Коэффициент трансформации будет равен: ens.tpu.ru 43. Явление взаимной индукции. Трансформатор.Рассмотрим два неподвижных контура (1 и 2), которые расположены достаточно близко друг от друга (рис. 1). Если в контуре 1 протекает ток I1, то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I1. Обозначим через Ф21 часть потока,пронизывающая контур 2. Тогда (1) где L21 — коэффициент пропорциональности. Если ток I1 меняет свое значение, то в контуре 2 индуцируется э.д.с. ξi2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф21, который создается током в первом контуре и пронизыващет второй: Аналогичным образом, при протекании в контуре 2 тока I2 магнитный поток (его поле изображено на рис. 1 штрихами) пронизывает первый контур. Если Ф12 — часть этого потока, который пронизывает контур 1, то Если ток I2 меняет свое значение, то в контуре 1 индуцируется э.д.с. ξi1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф12, который создается током во втором контуре и пронизывает первый: Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L21 и L12 называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L21 и L12 равны друг другу, т. е. (2) Коэффициенты пропорциональности L12 и L21 зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн). Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 2). Магнитная индукция поля, которое создавается первой катушкой с числом витков N1, током I1 и магнитной проницаемостью μ сердечника, B = μμ0(N1I1/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф2 = BS = μμ0(N1I1/l)S Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N2 витков, Поток Ψ создается током I1, поэтому, используя (1), найдем (3) Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L12 получим выражение в соответствии с формулой (3). Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник, Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока Закон ФарадеяСм. также: Электромагнитная индукция ЭДС, создаваемая во вторичной обмотке, может быть вычислена по закону Фарадея, который гласит, что:
Где U2 — Напряжение на вторичной обмотке, N2 — число витков во вторичной обмотке, Φ — суммарный магнитный поток, через один виток обмотки. Если витки обмотки расположены перпендикулярно линиям магнитного поля, то поток будет пропорционален магнитному полю B и площади S через которую он проходит. ЭДС, создаваемая в первичной обмотке, соответственно:
Где U1 — мгновенное значение напряжения на концах первичной обмотки, N1 — число витков в первичной обмотке. Поделив уравнение U2 на U1, получим отношение[6]:
studfiles.net Основы электроники. Индуктивность и трансформатор.Продолжаем изучать электронику! Напоминаю, что начать мы решили с самого легкого, но в то же время самого важного, а именно с азов электроники, с основных элементов, которые можно встретить в любой принципиальной схеме. И вот сегодня пришло время поговорить про индуктивности. Для того, чтобы не было недопонимания, сразу поясню, что термин индуктивность может означать как физическую величину (типа емкости, сопротивления), так и элемент схемы – катушку индуктивности (типа конденсатор, резистор). В принципе точно также конденсаторы называют емкостями, а резисторы сопротивлениями ) Итак, единица индуктивности – Генри, а на практике чаще мГн или мкГн. Для понимания работы индуктивности как элемента, давайте сравним ее с конденсатором. Поехали… В конденсаторе – если пропустить через него ток, то это вызовет нарастание напряжения на нем. В катушке – если приложить к ней напряжение, то произойдет увеличение тока через индуктивность. Да короче, если в двух словах, то индуктивность, по сути – противоположность конденсатора. В конденсаторе скорость изменения напряжения зависит от протекающего тока. А в катушке? Правильно, наоборот! Скорость изменения тока зависит от приложенного напряжения. Практическое применение индуктивностей настолько обширно, что не будем сейчас это обсуждать отдельно ) Кстати, совсем забыл! Вот обозначение катушек индуктивности на схемах: Последовательное соединение Параллельное соединение индуктивностей Вот так вот все просто 😉 Идем дальше… Думаю, вы уже поняли, что катушки индуктивности нужные и очень полезные элементы. А что может быть круче индуктивности? Конечно две индуктивности! Почему? А все просто, две связанные катушки индуктивности представляют собой полезнейшую вещицу – трансформатор! Катушки, входящие в трансформатор, называют первичной и вторичной обмотками трансформатора. Мы подаем на первичную обмотку трансформатора входное напряжение, а со вторичной снимаем уже другое напряжение, причем коэффициент трансформации (изменения) пропорционален отношению числа витков катушек. Очень важным свойством трансформаторов является то, что мощность на его выходе практически равна мощности на входе. Что это нам дает? А то, что, если у нас есть, например, понижающий трансформатор, то на выходе мы получим рост тока при уменьшении напряжения. Мощность при этом естественно не изменится. Давайте теперь прикинем, где бы мы могли использовать трансформаторы и для чего.Ну, во-первых, катушки в трансформаторе электрически изолированы друг от друга, а, значит, трансформатор может помочь нам защитить нашу схему от непосредственного контакта с силовой сетью. А, во-вторых, при помощи этого замечательного устройства мы можем преобразовать переменное напряжение сети к другому значению, как к большему, так и к меньшему. К слову, чаще всего напряжение сети понижается при помощи трансформатора. Это, пожалуй, основное применение этих элементов ) Вот так вот кратко обсудили мы индуктивности и трансформаторы, в принципе, для понимания сути работы этих элементов этого вполне достаточно, а нам как раз это и нужно. А практическое применение всех элементов, разработку схем с нуля, а также разводку плат, все это мы рассмотрим в будущем, и вот тогда нам очень пригодится то, что описано в первых статьях рубрики «Электроника для начинающих». Опять повторюсь, что очень важно понять, именно понять, а не запомнить азы электроники и основополагающие принципы работы основных элементов;) В общем, до скорой встречи в будущих статьях! P.S. Предыдущие статьи серии тут и и вот тут 😉 microtechnics.ru 51. Взаимная индукция. Трансформаторы. Коэффициент трансформации.Возьмем два контура, расположенные недалеко друг от друга, как это показано на рисунке. В первом контуре течет ток . Он создает магнитный поток, который пронизывает и витки второго контура.
При изменении тока во втором контуре наводится ЭДС индукции:
Аналогично, ток второго контура создает магнитный поток, пронизывающий первый контур:
И при изменении тока наводится ЭДС:
Контуры называются связанными, а явление – взаимной индукцией. Коэффициенты иназываютсявзаимной индуктивностью, или коэффициентами взаимной индукции. Причём Трансформатор является типичным примером двух связанных контуров. Рассмотрим индуктивность трансформатора и найдем коэффициент трансформации. Итак, явление взаимной индукции используется в широко распространенных устройствах – трансформаторах. Трансформатор был изобретен Яблочковым, русским ученым, в 1876 г. для раздельного питания отдельных электрических источников света (свечи Яблочкова). Рассчитаем взаимную индуктивность двух катушек и , намотанных на общий сердечник (рис). Когда в первой катушке идет ток , в сердечнике возникает магнитная индукцияи магнитный потокФ через поперечное сечение S. Магнитное поле тороида можно рассчитать по формуле Через вторую обмотку проходит полный магнитный поток , сцепленный со второй обмоткой: здесь – потокосцепление, которое можно найти по формуле: По определению, взаимная индуктивность двух катушек равна: К первичной обмотке подключена переменная ЭДС . По закону Ома ток в этой цепи будет определяться алгебраической суммой внешней ЭДС и ЭДС индукции. где – сопротивление обмотки. –делают малым (медные провода) и . Тогда Во второй обмотке, по аналогии, , отсюда
Если пренебречь потерями, т.е. предположить, что , то
Коэффициент трансформации будет равен: 52. Самоиндукция. Токи замыкания и размыкания цепи. Экстраток размыкания.Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I: Φ = LI. Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называетсягенри (Гн). Индуктивность контура или катушки равна 1 Гн, если при силе постоянного тока 1 А собственный поток равен 1 Вб:
В качестве примера рассчитаем индуктивность длинного соленоида, имеющего N витков, площадь сечения S и длину l. Магнитное поле соленоида определяется формулой где I – ток в соленоиде, n = N / e – число витков на единицу длины соленоида. Магнитный поток, пронизывающий все N витков соленоида, равен
Следовательно, индуктивность соленоида равна L = μ0 n2 S l = μ0 n2 V, где V = Sl – объем соленоида, в котором сосредоточено магнитное поле. Полученный результат не учитывает краевых эффектов, поэтому он приближенно справедлив только для достаточно длинных катушек. Если соленоид заполнен веществом с магнитной проницаемостью μ, то при заданном токе I индукция магнитного поля возрастает по модулю в μ раз; поэтому индуктивность катушки с сердечником также увеличивается в μ раз: Lμ = μ L = μ0 μ n2 V ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно закона Фарадея равна ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней. При любом изменении силы тока в проводящем контуре возникает э.д.с. самоиндукции, после чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, по правилу Ленца, всегда имеют такое направление, чтобы оказывать сопротивление изменениям тока в цепи, т. е. имеет направление, противоположное току, создаваемому источником. При выключении источника тока экстратоки так же направлены, как и ослабевающий ток. Значит, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи. Исследуем процесс выключения тока в цепи, содержащей источник тока с э.д.с. ξ , катушку индуктивностью L и резистор сопротивлением R . Под действием внешней э. д. с. в цепи течет постоянный ток (пренебрегаем внутренним сопротивлением источника тока). В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет убывать, что приведет к возникновению э.д.с. самоиндукции ξs = -L(dI/dt) оказывающей препятствие, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи задается законом Ома I= ξs/R, или (1) Разделив в формуле (1) переменные, получим (dI/I) = -(R/L)dt . Интегрируя эту формулу по I (от I0 до I) и t (от 0 до t), найдем ln (I/I0) = –Rt/L, или (2) где τ = L/R — постоянная, которая называется временем релаксации. Из (2) видно, что τ есть время, в течение которого сила тока уменьшается в е раз. Значит, в процессе отключения источника тока сила тока уменьшается по экспоненциальному закону (2) и задается кривой 1 на рис.. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше τ и, значит, тем медленнее убывает ток в цепи при ее размыкании. При замыкании цепи помимо внешней э. д. с. ξ возникает э. д. с. самоиндукции ξs = -L(dI/dt) оказывающая препятствие, согласно правилу Ленца, возрастанию тока. По закону Ома, IR = ξ+ξs или Зададим переменную u = (IR - ξ) преобразуем эту формулу как где τ — время релаксации. В момент замыкания (t=0) сила тока I = 0 и u = –ξ . Значит, интегрируя по u и (от –ξ до IR–ξ) и t (от 0 до t), найдем ln[(IR–ξ)]/(–ξ) = -t/τ, или (3) где I0=ξ/R — установившийся ток (при t→∞). Значит, в процессе включения источника тока увеличение силы тока в цепи определяется функцией (3) и кривой 2 на рис. Сила тока увеличивается от начального значения I=0 и асимптотически стремится к установившемуся значению I0=ξ/R . При этом, скорость нарастания тока задается тем же временем релаксации τ = L/R, что и убывание тока. Установление тока осуществляется тем быстрее, чем меньше индуктивность цепи и чем больше ее сопротивление. Оценим значение э.д.с. самоиндукции ξs , которая возникает при мгновенном нарастании сопротивления цепи постоянного тока от R0до R. Допустим, что мы размыкаем контур, когда в нем течет установившийся ток I0=ξ/R . При размыкании цепи ток будет менеться по формуле (2). Подставив в нее формулу для I0 и τ, найдем Э.д.с. самоиндукции т. е. при значительном возрастании сопротивления цепи (R/R0>>1), которая обладает большой индуктивностью, э.д.с. самоиндукции может во много раз быть больше э.д.с. источника тока, включенного в цепь. Значит, необходимо учитывать, что контур, который содержит индуктивность, нельзя резко размыкать, так как при этом (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и поломке измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции больших значений не достигнет. studfiles.net Выходной трансформатор — почти просто, но не дешевоВведениеВокруг выходных трансформаторов для ламповых усилителей в последние годы создан некий ореол мистики и таинственности, знания, доступного лишь избранным. Отчасти так и есть, однако… Методики инженерного расчета трансформаторов были разработаны более полувека назад и за эти годы претерпели несущественные изменения лишь в части использования новых магнитных материалов более высокого качества [1]. Основные же принципы и расчетные соотношения остались прежними. Законы физики не изменяются за полста лет… Расчёт параметров выходного трансформатораИсходные данные для расчета трансформатора определяются в процессе расчета оконечного каскада усилителя. Ими являются — выходная мощность, приведенное сопротивление нагрузки в цепи анода, индуктивность первичной обмотки и индуктивность рассеяния трансформатора [2]. Определение необходимых размеров магнитопроводаПервоначально надо определить требуемый габарит магнитопровода. Пригодность имеющегося железа можно ориентировочно оценить по условию:
где Vc — активный объем стали;
L1 — расчетная индуктивность первичной обмотки, Гн; UA — амплитуда напряжения на зажимах первичной обмотки, В; FH — нижняя граничная частота, Гц; Bmax — максимальная амплитуда магнитной индукции, Гс. S — площадь сечения магнитопровода, см2; lC — средняя длина магнитной силовой линии, см. Для броневого магнитопровода средняя длина магнитной силовой линии рассчитывается, как:
А для стержневого:
где обозначения соответствуют принятым на Рис. 1.
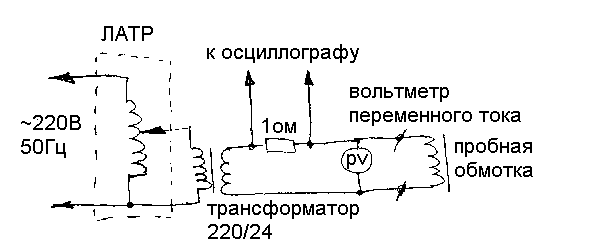
Рис. 1 Основные размеры магнитопроводов При оценке габаритов магнитопровода величину Вmax следует ориентировочно принять равной 7000 — 8000 Гс для пластинчатых и 10000 Гc для витых разрезных наборов железа. Экспериментальное определени индукции трансформатораДля дальнейших расчетов максимальное значение индукции Вmax желательно определить экспериментально на выбранном железе. С этой целью на каркас трансформатора наматывается пробная обмотка в 100 витков и включается в схему по Рис. 2. Магнитопровод при этом должен быть собран без зазора. Плавно увеличивая напряжение на обмотке с помощью ЛАТРа, наблюдают форму тока через нее. В момент появления заметных на глаз искажений формы синусоиды фиксируют напряжение на обмотке (показания прибора V1).
Рис. 2 Схема для измерения максимальной индукции в магнитопроводе Затем допустимое значение индукции рассчитывают по формуле:
где U1 — показания прибора, В; S — площадь сечения магнитопровода, см2 (чистого железа). Определение коэффициента трансформацииРасчет конструктивных данных начинают с определения коэффициента трансформации, который, при заданной величине сопротивления нагрузки усилителя, обеспечит расчетную величину анодной нагрузки выходной лампы.
где n — коэффициент трансформации; N1 — число витков первичной обмотки; N2 — число витков вторичной обмотки; RA — расчетная величина сопротивления анодной нагрузки лампы, Ом; RH — сопротивление нагрузки усилителя, Ом; К — КПД трансформатора. Величина КПД однотактных трансформаторов на мощности 5 — 30 Вт обычно лежит в пределах 0,8 — 0,9. За значение сопротивления нагрузки усилителя желательно принять величину, равную:
где Rном — номинальное сопротивление акустической системы; Rmin — минимальное сопротивление акустической системы в рабочем диапазоне частот. Такая величина является компромиссной с точки зрения обеспечения как расчетного сопротивления анодной нагрузки лампы в номинальных условиях с одной стороны, так и коэффициента демпфирования с другой. Расчёт числа витков первичной обмоткиЧисло витков первичной обмотки вычисляется из условия непревышения максимально допустимого значения индукции в магнитопроводе:
где U1M — максимальная амплитуда напряжения на зажимах первичной обмотки, В; ВМП — максимально допустимая амплитуда переменной составляющей индукции, Гс.
где ВM — изморенное ранее значение максимальной индукции, Гс. Опыт расчета и изготовления значительного количества разнообразных трансформаторов (как выходных, так и межкаскадных) позволяет сделать вывод, что значение ВМП не должно превышать 3500 — 4000 Гс для пластинчатых магнитопроводов (шихтованных) и 5000 Гс для витых разрезных (ленточных). Следует отметить, что витые сердечники, несмотря на более высокие качественные параметры в силовых трансформаторах, несколько уступают пластинчатым для применения в выходных. Искажения сигнала, вносимые трансформатором из-за нелинейности характеристики В/Н при использовании витых магнитопроводов проявляются при меньших значениях индукции, хотя, после появления, нарастают медленнее. Это явление объясняется тем, что магнитный поток концентрируется во внутренних витках магнитопровода, где длина силовой линии короче. В результате сердечник постепенно насыщается, начиная от внутренних слоев и заканчивая внешними. Внутренние слои оказываются насыщенными гораздо раньше внешних, что проявляется в виде небольшого искривления характеристики намагничивания железа даже при средней индукции 4000 — 6000 Гс. Более высокое качество железа витых сердечников несколько смягчает этот эффект, но полностью устранить не может. Количество витков первичной обмотки можно определить и по другой формуле, исходя из условия обеспечения расчетной индуктивности:
где L1 требуемая индуктивность обмотки, Гн; m — магнитная проницаемость материала сердечника при заданных ампер-витках постоянного подмагничивания. Однако, практика показывает, что расчет по формуле (10) приводит к заниженному числу витков по сравнению с (8), а это недопустимо из-за резкого роста искажений на низких частотах вследствие насыщения магнитопровода. Только при высокой нижней граничной частоте (более 100 — 150 Гц) формула (10) дает большее значение числа витков. Кроме того, она неудобна тем, что в расчет входит величина m , зависящая от ампер-витков постоянного подмагничивания, определить которую до экспериментального изготовления трансформатора можно лишь приблизительно по графикам соответствующих зависимостей [1], [3], [4]. Расчёт числа витков вторичной обмоткиЧисло витков вторичной обмотки рассчитывается как:
Расчёт диаметра проводаДиаметр провода (чистой меди) первичной обмотки:
Формула (13a) справедлива для расчета средней длины витка на броневом сердечнике (Рис. 1а), а формула (13b) — на стрежневом (Рис. Ч в), величина dk (см) — толщина материала каркаса. Диаметр провода вторичной обмотки:
Если вторичная обмотка состоит из нескольких параллельно соединенных секций, то диаметр провода секции рассчитывают как:
Размещение обмоток трансформатораПосле расчета обмотки необходимо проверить их размещение в окне магнитопровода. Наилучшим считается такое размещение, когда и первичная и вторичная обмотки укладываются в целое число слоев и полностью заполняют окно магнитопровода. Для достижения такого результата допустимо варьировать число витков и диаметр провода обмоток в небольших пределах (до _* 10%). Заполнение окна магнитопроводаможно проверить по формулам:
где A1 , А2, Aиз — толщины первичной обмотки , вторичной обмотки и межобмоточной изоляции; р1, р2 — число слоев первичной и вторичной обмоток; d`1, d`2 -диаметры проводов с изоляцией первичной и вторичной обмоток; dиз — толщина межслойной изоляции. Индуктивность рассеяния трансформатора достаточной точностью определяется по формуле;
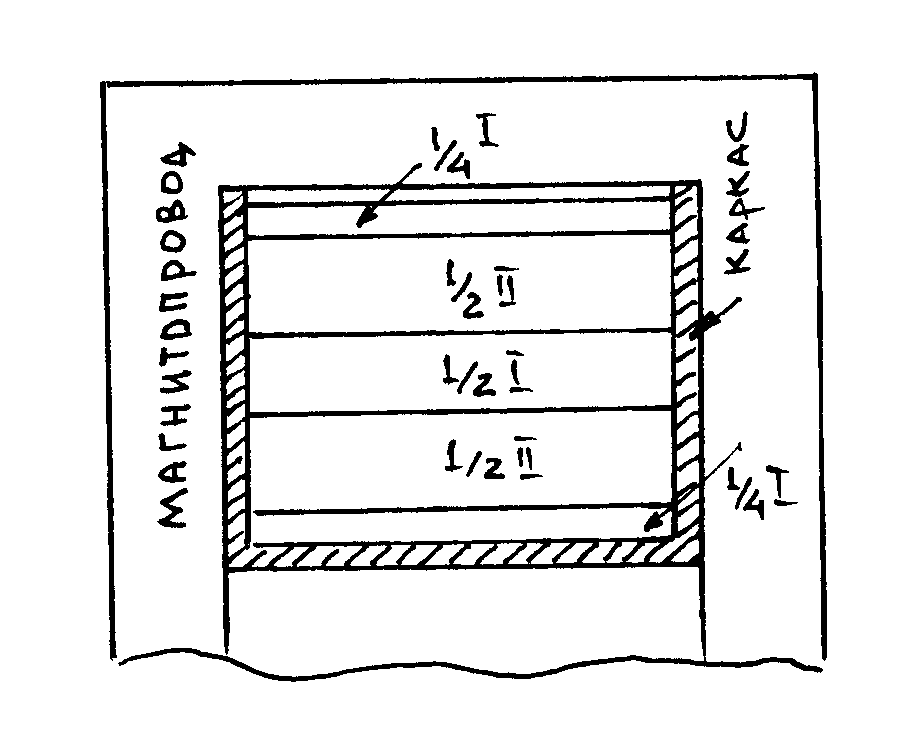
где l0 — средняя длина витка, см; h' — высота намотки слоя, см; к — количество секций. Для получения расчетной величины индуктивности рассеяния, обмотки трансформатора в большинстве случаев необходимо секционировать. Наиболее просто и эффективно выполнить послойное
Рис. 3 Пример размещения обмоток в окне магнитопровода (цилиндрическое секционирование) (цилиндрическое) секционирование, когда обмотки наматываются на каркас частями, а в конце соединяются последовательно или параллельно. Чаще всего применяют последовательное включение секций первичной обмотки и параллельное — вторичной. Суммарное число секций первичной и вторичной k должно быть таким, чтобы индуктивность рассеяния LS, вычисленная по (17), не превышала найденную при электрическом расчете оконечного каскада. Один из вариантов размещения секций на каркасе приведен на Рис. 3. Необходимо помнить, что общее число секций первичной и вторичной обмотки должно быть нечетным, а крайние секции (т.е. непосредственно лежащая на каркасе и внешняя) должны принадлежать одной обмотке и иметь половинное число витков по отношению к внутренним секциям той же обмотки. Только в этом случае выполняется условие компенсации полей рассеяния соседних секций и индуктивность рассеяния будет соответствовать расчетной. Если обмотка распределена на двух катушках (стержневые трансформаторы), то секции ее должны чередоваться от одной катушки к другой. Это условие относится и к двухтактным трансформаторам, где обмотки каждого плеча обязательно должны иметь одинаковое число секций на одном и на другом стержнях магнитопровода. Определение величины немагнитного зазораНеотъемлемой конструктивной особенностью трансформатора выходного однотактного каскада является немагнитный зазор между частями магнитопровода. При его отсутствии постоянная составляющая анодного тока выходной лампы, протекающая через первичную обмотку, вызывает насыщение железа и, как следствие, происходит катастрофическое падение магнитной проницаемости и возрастание искажений, вносимых трансформатором. Зазор не позволяет магнитопроводу войти в насыщение от постоянного подмагничивания (поскольку он эквивалентен многократному увеличению длины магнитной силовой линии для постоянной составляющей магнитного потока) и, в то же время, не влечет за собой драматического снижения величины m . Оптимальным является такой немагнитный зазор, при котором индукция, соответствующая постоянной составляющей магнитного потока, находилась бы примерно на середине линейной части характеристики намагничивания. Для наиболее распространенных типов электротехнической стали величина зазора может быть ориентировочно определена по формуле:
I0 — ток постоянного подмагничивания, А; lC — длина силовой линии, см. Более точно величину зазора подгоняют экспериментально при номинальном токе подмагничивания, исходя из условий получения наибольшей выходной мощности на нижней граничной частоте и минимальных искажении при половине номинальной выходной мощности на той же частоте сигнала. Поскольку теоретический расчет оптимального зазора достаточно сложен и требует значительного количества экспериментальных данных о качестве применяемого железа, то представляется более целесообразным использовать практический подбор зазора в готовом трансформаторе. Паразитные ёмкости и методы борьбы с нимиВ заключение следует обратить внимание на такие неприятные и неизбежные явления, как межобмоточная и распределенная емкости трансформатора. Совместно с индуктивностями обмоток (или их частями) и индуктивностями рассеяния, они образуют паразитные колебательные контуры, резонирующие в области верхних звуковых и ультразвуковых частот. Эти резонансы искажают частотную и фазовую характеристики трансформатора (набег фазы из-за распределенной емкости плохо сконструированного трансформатора на высших частотах может достигать 400° — 7000° и, кроме того, быть немонотонным). Радикального средства борьбы с этими явлениями нет, но уменьшить их можно следующими способами:
Пропитка катушки трансформатора различными компаундами имеет как достоинства, так и недостатки. К первым относится увеличение механической прочности и снижение резонансов конструкции. Ко вторым — увеличение паразитных емкостей и снижение частот паразитных электрических резонансов вплоть до звукового диапазона. Решение о пропитке трансформатора должно приниматься только после тщательного анализа всех "за" и "против". ЗаключениеИ, наконец, хотелось бы напомнить, что выходной трансформатор — это клубок компромиссов. Не следует гнаться за идеальными параметрами и огромной массой: в 99% случаев улучшение одного параметра ведет к ухудшению нескольких других. Излишнее количество секций увеличивает межобмоточную емкость; излишнее число витков — индуктивность рассеяния и активное сопротивление. Таких примеров множество. При расчете задавайтесь разумными исходными параметрами и не делайте из трансформатора противовес для башенного крана. Не требуйте от трансформатора невозможного, но разумно используйте то, что он может предоставить. Литература
vt-tech.eu 2. Взаимная индукция. ТрансформаторЯвление взаимной индукции заключается в наведении ЭДС индукции в проводнике, находящемся вблизи цепи переменного тока. Из закона электромагнитной индукции Фарадея следует, что ЭДС взаимной индукции равна (16.1) где – магнитный поток через поверхность, ограниченную вторым контуром, обусловленный магнитным полем тока, протекающего в первом контуре (рис. 16.1). Рис. 16.1 Чем больше сила тока в первом контуре, тем больше магнитный поток, обусловленный этим током. Поэтому, так же как и при самоиндукции, этот магнитный поток пропорционален силе тока (16.2) где, как говорилось выше, коэффициент пропорциональности называется взаимной индуктивностью (статической взаимной индуктивностью) второго и первого контуров. Этот коэффициент зависит от геометрических размеров, формы, количества витков, взаимного расположения первого и второго контуров, от магнитной проницаемости среды, в которой они находятся. Если источник тока отключить от первого контура и подключить ко второму, создав ток , то для магнитного потока через площадь первого контураможно записать аналогичную формулу . Пусть контуры находятся в неферромагнитной среде, тогда, как можно показать, для них выполняется так называемая теорема взаимности, согласно которой коэффициенты взаимной индуктивности равны друг другу численно и имеют одинаковые знаки
Если же среда ферромагнитная, причем режим перемагничивания среды выходит за пределы обратимого процесса, то изависят не только от вышеперечисленных параметров, но и от величины токов в контурах. В этом случае теорема взаимности не выполняется. Заменив в законе Фарадея (16.1) магнитный поток его выражением (16.2) и полагая , получим (16.3) Если первый и второй контуры находятся в ферромагнитной среде, то можно пользоваться формулой, по виду аналогичной формуле (16.3): (16.4) где – так называемая динамическая взаимная индуктивность второго и первого контуров. На явлении взаимной индукции основано действие трансформаторов, которые применяются для повышения или понижения напряжения переменного электрического тока. Трансформатор (рис. 16.2) состоит из двух или нескольких соленоидальных обмоток, расположенных близко друг от друга и чаще всего закрепленных на общем ферромагнитном сердечнике. Концы пер-вичной обмотки присоединены к источнику переменного тока, а кон- цы вторичной обмотки включены в цепь потребителя электрической энергии. Переменное магнитное поле тока , протекающего в первичной обмотке трансформатора, вызывает появление ЭДС взаимной индукции во вторичной обмотке. Магнитное поле первичной обмотки практически полностью локализовано в ферромагнитном сердечнике, играющем роль магнитной цепи. Поэтому применение в трансформаторе такого замкнутого сердечника, общего для обеих обмоток, позволяет резко увеличить магнитный поток взаимной индукции и взаимную индуктивность. Определим статическую и динамическую взаимные индуктивности обмоток трансформатора.
N1 N2 Рис. 16.2 Пусть Ф – магнитный поток в сердечнике. Тогда магнитный поток через витков вторичной обмотки равен
Следовательно, из формул (16.2) и (16.4) получим . (16.5) Статическая и динамическая индуктивности первичной обмотки трансформатора в режиме холостого хода, соответствующего разомкнутому состоянию вторичной цепи ,равны . (16.6) ЭДС самоиндукции в первичной обмотке можно выразить формулой
Найдем отношение абсолютных значений напряжений ина концах вторичной и первичной обмоток при холостом ходе, называемое коэффициентом трансформации. При разомкнутой вторичной обмотке (холостой ход) . В этом случае напряжение на ее концах численно равно ЭДС взаимной индукции (16.7) На концах первичной обмотки напряжение , как можно показать с помощью закона Ома, равно (16.8) где – ЭДС источника тока;– внутреннее сопротивление источника тока, подключенного к первичной обмотке трансформатора. Сила тока в первичной обмотке согласно закону Ома для замкнутой цепи определяется формулой
где – ЭДС самоиндукции в первичной обмотке;– сопротивление первичной обмотки. Выражая и подставляя в (16.8), получаем Как правило, для трансформаторов первый член в правой части пренебрежимо мал по сравнению со вторым. Поэтому приближенно можно считать, что (16.9) Зная и, используя формулы (5),(6),(7),(9), находим коэффициент трансформации . (16.10) studfiles.net |
|
|||||||||||||||||
|
|
|||||||||||||||||
|











 И, по традиции, давайте рассмотрим параллельное и последовательное соединения индуктивностей. Там все просто, так же как и при соединении резисторов.
И, по традиции, давайте рассмотрим параллельное и последовательное соединения индуктивностей. Там все просто, так же как и при соединении резисторов. ![Rendered by QuickLaTeX.com \[L_общ = L_1 + L_2 + L_3\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-42854cfb4df39de9c0052672ac235bc0_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{L_общ} = \frac{1}{L_1} + \frac{1}{L_2} + \frac{1}{L_3}\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-451cc638201fc258faa6b5142afeeb0a_l3.png)
 Принцип работы трансформатора заключается в следующем.
Принцип работы трансформатора заключается в следующем.