Измерение реактивной мощности в трехфазной цепи. Мощность трехфазной цепи переменного тока17. Преимущества трехфазных систем. Мощность в трехфазной цепи. Способы измерения активной и реактивной мощности в трехфазных цепях.В современных системах передачи электрической энергии на дальние расстояния, электроснабжения и распределения электрической энергии применяются трехфазные цепи, которые по сравнению с однофазными имеют значительные преимущества:
Мощность трехфазной цепиМощность трехфазной цепи – это сумма соответствующих мощностей всех трех фаз (потерями мощности в нейтральном проводе обычно пренебрегают):
Как и в однофазной цепи активная, реактивная и полная мощности трёхфазной цепи связаны соотношением: . Мощность любой из фаз выражается обычной формулой: . В случае симметричной нагрузки мощности всех трёх фаз соответственно равны:
и для мощности трёхфазной цепи можно записать: . В трёхфазной цепи при симметричной нагрузке: , поэтому для мощности трёхфазной цепи можно записать: Кроме того, при симметричной нагрузке известны соотношения между линейными и фазными напряжениями и токами: I Л = I Ф , U Л U Ф - при соединении по схеме «звезда», I Л I Ф , U Л = U Ф - при соединении по схеме «треугольник». После подстановки этих выражений в формулу мощности трёхфазной цепи в общем случае при симметричной нагрузке получаем: . В случае несимметричной нагрузки мощность трёхфазной цепи следует находить как сумму соответствующих мощностей всех трёх фаз (т.е. как сумму соответствующих фазных мощностей): Измерение активной мощности трёхфазной цепи Активная мощность в цепи переменного тока P = I U cos φ измеряется с помощью электродинамического ваттметра, измерительный механизм которого состоит из двух катушек, одна из которых может вращаться. Обмотка неподвижной катушки – последовательная или токовая обмотка – обладает малым сопротивлением и включается в измеряемую цепь последовательно, а обмотка подвижной катушки - обмотка напряжения - имеет большое сопротивление и включается параллельно на зажимы нагрузки (потребителя). где k - конструкционный коэффициент, I - ток в последовательной обмотке ваттметра. При включении ваттметра в цепь следует обращать внимание на правильное подключение обмоток ваттметра, начала которых ( генераторные зажимы) обозначаются звёздочками (* ). Оба генераторных зажима должны быть присоединены к одному и тому же проводу со стороны источника электрической энергии (генератора). Для измерения активной мощности трёхфазной цепи часто используется однофазный ваттметр активной мощности, включаемый по различным схемам.
Метод одного ваттметра применяется в трёхфазных цепях только при симметричной нагрузке фаз. При симметричной нагрузке мощность, потребляемая каждой из трёх фаз, одинакова, поэтому достаточно измерить мощность одной фазы и, умножив результат измерения на число фаз, получить мощность трёхфазной цепи: . Следовательно, для измерения мощности при симметричной нагрузке достаточно одного ваттметра, токовая обмотка которого включается последовательно с фазной нагрузкой, а обмотка напряжения – включается на фазное напряжение.
Если нейтральная точка нагрузки недоступна, то измерение фазной мощности в соединении звезда выполняют по схеме с искусственной нейтральной точкой, созданной соединёнными в звезду обмоткой напряжения ваттметра Z Vи двух равных ей по сопротивлению добавочных резисторов Z 2 и Z 3 : . studfiles.net Расчет трехфазных цепей6. Расчёт трёхфазных цепей. Многофазной системой электрических цепей называют совокупность электрических цепей, в которых действуют синусоидальные ЭДС одной и той же частоты, сдвинутые друг относительно друга по фазе, создаваемые общими источником энергии (ГОСТ 19880-74). Многофазной цепью называют многофазную систему электрических цепей в которой отдельные фазы электрически соединены друг с другом (ГОСТ 19880-74). В частности при числе фаз многофазной системы равной 3 будем иметь трехфазную цепь. Различают симметричную и несимметричную многофазную систему. Симметричной многофазной системой токов называют многофазную систему электрических токов в которой отдельные электрические токи равны по амплитуде и отстают по фазе относительно друг друга на углы равные , гдеm – число фаз. (ГОСТ 19880-74). Несимметричной многофазной системой электрических токов называют систему не удовлетворяющую любому из вышеуказанных признаков (ГОСТ 19880-74). 6.1. Трехфазная система ЭДС. Под трёхфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе относительно друг друга на 120°.
, ,. Соответственно, для действующих ЭДС в комплексной форме можно записать , , и изобразить на комплексной плоскости
6.2. Общие положения и допущения при расчете трехфазных цепей. Трехфазные цепи являются разновидностью цепей синусоидального тока и поэтому их расчет производится теми же методами и приёмами, которые присущи цепям однофазного синусоидального тока. Для анализа трехфазных цепей применим комплексный (символический) метод расчета, могут строиться векторные и топографические диаграммы. Для анализа трехфазных цепей введем два допущения, которые сводятся к тому, что синусоидальное напряжение на зажимах трехфазного генератора симметричны при любой нагрузке:
6.3.Расчет соединения звезда-звезда с нулевым проводом. Предположим сейчас и в дальнейшем, что сопротивление проводов, соединяющих источник с нагрузкой, равно нулю. В этом случае в схеме образуются три обособленных контура. Токи в них , ,, где ,и- линейные токи, а,и- фазные токи, токи в нагрузке, соответственно, фазыa, b, c. Ток в нулевом проводе равен . Напряжение между линейным проводом и нулевым узлом- фазное напряжение:,и. Напряжение между линейными проводами- линейное напряжение: , и . При соединении звезда-звезда с нулевым проводом, справедливы следующие соотношения для токов: ,и; или для модулей:; для напряжений:,,и,,; или для модулей:. Симметричная цепь (нагрузка). Симметричная многофазная (трёхфазная) цепь – это цепь, в которой комплексные сопротивления, составляющих её фаз, одинаковы (ГОСТ 19880-74). На рисунке представлена векторная диаграмма напряжений на источнике и нагрузке. Векторная диаграмма токов построена для симметричной цепи ак-тивного характера. При этом и, следовательно, нулевой провод может быть устранён из цепи без изме-нения режима её работы. Аннало-гичная ситуация наблюдается и для симметрич-ной цепи с ак-тивно-реактивной нагрузкой, когда. Несимметричная цепь (нагрузка). Если нагрузка несимметрична, то есть , то появляется ток в нулевом проводе:. Как это, например, показано на векторной диаграмме, когда сопротивления фаз равны по величине, но имеют различный характер: в фазе - активная нагрузка, в фазе- индуктивная нагрузка, а в фазе- емкостная нагрузка.
6.4. Расчет соединения звезда-звезда без нулевого провода. Симметричная цепь (нагрузка). Вслучае симметричной цепи расчет токов в фазах нагрузки сводится к расчету соединения звезда-звезда с нулевым проводом, как это было показано в пункте 6.3. , ,. Несимметричная нагрузка. В случае несимметричной цепи напряжение на фазе нагрузки не равно соответствующему напряжению источника. Для определения искомого тока ,инеобходимо отыскать фазное напряжение на нагрузке. Для этого следует записать уравнение по второму закону Кирхгофа для контуров, образованных источником ЭДС, сопротивлением нагрузки и напряжением холостого хода между узлами :, откуда. Определение ,ив последних трёх выражениях возможно в случае, когда известно - напряжение смещения нейтрали. Напряжение смещения нейтрали можно определить по методу двух узлов, представляя илипри условии, что потенциал узлапринять равным нулю, тогда: . Если по условию проектирования нулевой провод обладает некоторой проводимостью, то последнее выражение можно переписать в виде: . При этом расчете было предположено, что сопротивления фазных обмоток генератора и сопротивления линейных проводов равны нулю. Если эти условия не соблюдаются, то эти сопротивления могут быть учтены путем их введения в сопротивления соответствующих фаз ,и. При отсутствии сопротивлений обмоток генератора их ЭДС равны фазным напряжениям на его зажимах,,и тогда полученную формулу для определения смещения нейтрали можно записать в виде: . 6.5. Расчет соединения треугольник-треугольник. Пусть сопротивление фазных обмоток генератора и сопротивления линейных проводов равны нулю, тогда: ,,. Ток в фазах нагрузки – фазный ток: , ,. Линейные токи в общем случае, то есть для несимметричной цепи можно определить по первому закону Кирхгофа: , ,. Для симметричной цепи линейные токи в раз больше фазных токов. 6.6. Активная, реактивная и полная мощности трёхфазной цепи. Под активной и реактивной мощностями понимают: и. Полная мощность:. Если нагрузка симметричная, то ,,и тогда мощность трёхфазной цепи, через фазные токи и напряжения:,,или через линейные токи и напряжения независимо от способа её соединения в звезду или треугольник,и. 6.7. Измерение активной мощности в трёхфазной цепи. Метод трёх ваттметров используют для измерения активной мощности трёхфазной цепи в случае несимметричной нагрузки. Активная мощность всей цепи равна сумме показаний всех ваттметров. При симметричной нагрузке достаточно измерить мощность одной из фаз и результат утроить – это, так называемый, метод одного ваттметра. В случае, если узел недоступен, то измерение мощности можно произвести двумя ваттметрами. и . Докажем, что сумма показаний двух ваттметров представляет собой активную мощность трехфазной цепи. Составим уравнение по второму закону Кирхгофа для контура, образованного фазными напряжениями и и линейным напряжением : , откуда; аналогично.
Сумма реальных частей каждого слагаемого соответствует активной мощности трехфазной цепи. studfiles.net Мощность трехфазной электрической цепи - FREEWRITERSТрехфазная электрическая цепь является совокупностью трех однофазных, поэтому активная и реактивная мощности трехфазной цепи равняются сумме соответствующих мощностей отдельных фаз. Для схемы соединения фаз потребителя "звездой" активная мощность трехфазной электрической цепи
Реактивная мощность для схемы "звезда": Реактивная мощность фазы
Полная мощность трехфазной цепи
Комплексная форма мощности схемы "звезда"
для схемы "треугольник"
У симметричного потребителя мощности всех фаз одинаковы. Тогда
Мощность симметричного потребителя определяется также через линейные напряжения и токи. При соединении "звезда"
При соединении "треугольник" Таким образом, для симметричного потребителя формулы мощности не зависят от схемы соединения потребителя. В трехфазной симметричной системе сумма мгновенных значений мощностей - величина постоянная и равняется активной мощности трехфазной цепи:
Мощность симметричной или несимметричной трехпроводной системы может измеряться всего двумя ваттметрами. Действительно, поскольку
Один ваттметр включают под ток ia и напряжение uac, второй - под ток ib и напряжение ubc (рис. 1).
Рис. 1. Для измерения активной мощности в четырехпроводной несимметричной системе необходимо три ваттметра - по одному в каждой фазе. Реактивную мощность Q трехфазной симметричной электрической цепи измеряют одним ваттметром, предназначенным для измерения активной мощности, если его включить так, как показано на рис. 2, а.
Рис. 2. Действительно, из векторной диаграммы, (рис. 2, б) и схемы включения (а) следует, что ваттметр показывает:
Чтобы найти реактивную мощность всей симметричной цепи, достаточно показания ваттметра умножить на В автономной энергосистеме (рис. 3) механическая энергия привода мощностью 30 кВт преобразуется в трехфазном генераторе в электрическую - мощностью 26,4 кВт (КПД генератора 0,88).
Рис. 3. По трехпроводной линии эта энергия поступает к потребителю для освещения и на приводы трехфазных двигателей. Чтобы повысить (до 0,9) коэффициент мощности
получается, что Для определения емкостей рассчитывается: активная мощность реактивная мощность и полная мощность Угол
Для желаемого угла
В автономной трехфазной системе выполняется условие баланса трех мощностей: активной, реактивной и полной. Для системы (рис.3) Рист = 26,4 кВт равняется суммарной активной мощности потребителя. freewriters.narod.ru Трехфазные электрические цепи (Лекция №16)Трехфазная цепь является частным случаем многофазных электрических систем, представляющих собой совокупность электрических цепей, в которых действуют ЭДС одинаковой частоты, сдвинутые по фазе относительно друг друга на определенный угол. Отметим, что обычно эти ЭДС, в первую очередь в силовой энергетике, синусоидальны. Однако, в современных электромеханических системах, где для управления исполнительными двигателями используются преобразователи частоты, система напряжений в общем случае является несинусоидальной. Каждую из частей многофазной системы, характеризующуюся одинаковым током, называют фазой, т.е. фаза – это участок цепи, относящийся к соответствующей обмотке генератора или трансформатора, линии и нагрузке. Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
Разработка многофазных систем была обусловлена исторически. Исследования в данной области были вызваны требованиями развивающегося производства, а успехам в развитии многофазных систем способствовали открытия в физике электрических и магнитных явлений. Важнейшей предпосылкой разработки многофазных электрических систем явилось открытие явления вращающегося магнитного поля (Г.Феррарис и Н.Тесла, 1888 г.). Первые электрические двигатели были двухфазными, но они имели невысокие рабочие характеристики. Наиболее рациональной и перспективной оказалась трехфазная система, основные преимущества которой будут рассмотрены далее. Большой вклад в разработку трехфазных систем внес выдающийся русский ученый-электротехник М.О.Доливо-Добровольский, создавший трехфазные асинхронные двигатели, трансформаторы, предложивший трех- и четырехпроводные цепи, в связи с чем по праву считающийся основоположником трехфазных систем.  Источником трехфазного напряжения является трехфазный генератор, на статоре
которого (см. рис. 1) размещена трехфазная обмотка. Фазы этой обмотки располагаются
таким образом, чтобы их магнитные оси были сдвинуты в пространстве друг относительно
друга на Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются: - экономичность передачи электроэнергии на большие расстояния; - самым надежным и экономичным, удовлетворяющим требованиям промышленного электропривода является асинхронный двигатель с короткозамкнутым ротором; - возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств; - уравновешенность симметричных трехфазных систем. Для рассмотрения важнейшего свойства уравновешенности трехфазной системы, которое будет доказано далее, введем понятие симметрии многофазной системы. Система ЭДС (напряжений, токов и т.д.) называется симметричной, если
она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.),
сдвинутых по фазе друг относительно друга на одинаковый угол
Из несимметричных систем наибольший практический интерес представляет двухфазная система с 90-градусным сдвигом фаз (см. рис. 4). Все симметричные трех- и m-фазные (m>3) системы, а также двухфазная система являются уравновешенными. Это означает, что хотя в отдельных фазах мгновенная мощность пульсирует (см. рис. 5,а), изменяя за время одного периода не только величину, но в общем случае и знак, суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС (см. рис. 5,б). Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на энергогенерирующей установке, сокращая срок ее службы. Эти же соображения относятся и к многофазным электродвигателям. Если симметрия нарушается (двухфазная система Тесла в силу своей специфики в расчет не принимается), то нарушается и уравновешенность. Поэтому в энергетике строго следят за тем, чтобы нагрузка генератора оставалась симметричной. Схемы соединения трехфазных систем Трехфазный генератор (трансформатор) имеет три выходные обмотки, одинаковые по числу витков, но развивающие ЭДС, сдвинутые по фазе на 120°. Можно было бы использовать систему, в которой фазы обмотки генератора не были бы гальванически соединены друг с другом. Это так называемая несвязная система. В этом случае каждую фазу генератора необходимо соединять с приемником двумя проводами, т.е. будет иметь место шестипроводная линия, что неэкономично. В этой связи подобные системы не получили широкого применения на практике. Для уменьшения количества проводов в линии фазы генератора гальванически связывают между собой. Различают два вида соединений: в звезду и в треугольник. В свою очередь при соединении в звезду система может быть трех- и четырехпроводной. Соединение в звезду На рис. 6 приведена трехфазная система при соединении фаз генератора и нагрузки в звезду. Здесь провода АА’, ВВ’ и СС’ – линейные провода. Линейным называется провод, соединяющий начала фаз обмотки генератора и приемника. Точка, в которой концы фаз соединяются в общий узел, называется нейтральной (на рис. 6 N и N’ – соответственно нейтральные точки генератора и нагрузки). Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным (на рис. 6 показан пунктиром). Трехфазная система при соединении в звезду без нейтрального провода называется трехпроводной, с нейтральным проводом – четырехпроводной. Все величины, относящиеся к фазам, носят название фазных переменных, к
линии - линейных. Как видно из схемы на рис. 6, при соединении в звезду
линейные токи Поскольку напряжение на источнике противоположно направлению его ЭДС, фазные
напряжения генератора (см. рис. 6) действуют от точек А,В и С к нейтральной
точке N; Линейные напряжения действуют между линейными проводами. В соответствии со вторым законом Кирхгофа для линейных напряжений можно записать
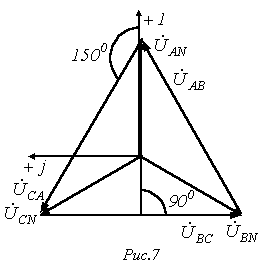
Отметим, что всегда На рис. 7 представлена векторная диаграмма для симметричной системы напряжений. Как показывает ее анализ (лучи фазных напряжений образуют стороны равнобедренных треугольников с углами при основании, равными 300), в этом случае
Обычно при расчетах принимается Соединение в треугольник В связи с тем, что значительная часть приемников, включаемых в трехфазные цепи, бывает несимметричной, очень важно на практике, например, в схемах с осветительными приборами, обеспечивать независимость режимов работы отдельных фаз. Кроме четырехпроводной, подобными свойствами обладают и трехпроводные цепи при соединении фаз приемника в треугольник. Но в треугольник также можно соединить и фазы генератора (см. рис. 8).  Для симметричной системы ЭДС имеем Таким образом, при отсутствии нагрузки в фазах генератора в схеме на рис. 8
токи будут равны нулю. Однако, если поменять местами начало и конец любой из
фаз, то Схема соединения фаз генератора и приемника в треугольник представлена на рис. 9. Очевидно, что при соединении в треугольник линейные напряжения равны соответствующим фазным. По первому закону Кирхгофа связь между линейными и фазными токами приемника определяется соотношениями
Аналогично можно выразить линейные токи через фазные токи генератора. На рис. 10 представлена векторная диаграмма симметричной системы линейных и фазных токов. Ее анализ показывает, что при симметрии токов
В заключение отметим, что помимо рассмотренных соединений «звезда - звезда» и «треугольник - треугольник» на практике также применяются схемы «звезда - треугольник» и «треугольник - звезда». Литература
Контрольные вопросы и задачи
www.toehelp.ru Измерение реактивной мощности в трехфазной цепи.Реактивную мощность в трехфазной трехпроводной цепи при симметричной нагрузке можно определить по разности показаний ваттметров(рис 8).
Рисунок 8. Измерение реактивной мощности двумя ваттметрами.
Откуда реактивная мощность:
Реактивную мощность в трехпроводной трехфазной цепи при симметричной нагрузке можно измерить одним ваттметром (рис 9).
Рисунок 9. Измерение Q одним ваттметром. Токовая обмотка ваттметра включается в линейныйпровод А, а обмотка напряжения – на линейное напряжение UBC(т. е. на «чужое» напряжение). Из векторной диаграммы (рис. 10) видно, что сдвиг фаз между током IA и напряжением UBCсоставляет α=90°- φ Рисунок 10.Векторная диаграмма. Тогда показания ваттметра
Для вычисления реактивной мощности трехфазной трехпроводной цепи при симметричной нагрузке необходимо показания ваттметра умножить на
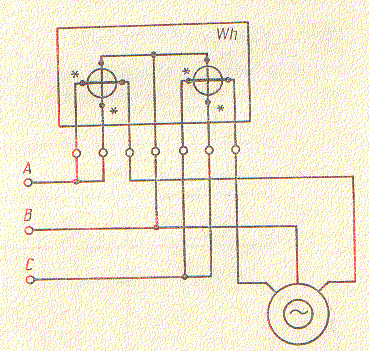
Измерение энергии в цепях переменного тока.В цепях переменного тока для измерения активной энергии служат однофазные и трехфазные счетчики индукционной системы. Для измерения активной энергии в однофазных и трехфазных цепях однофазные счетчики включают по схемам, аналогичным схемам включения ваттметров (см. рис. 3 и 5). В трехпроводных трехфазных цепях для измерения активной энергии применяют двухэлементные объединяющие измерительные системы двух однофазных счетчиков (рис. 11).
Рисунок 11. Измерительные системы двух однофазных счетчиков. Для измерения активной энергии в четырехпроводных цепях трехфазного тока применяют трехэлементные счетчики. Реактивную энергию WР как при симметричной, так и при несимметричной нагрузке в трехфазной цепи измеряют трехфазными индукционными счетчиками реактивной энергии. При симметричной нагрузке в трехпроводной трехфазной цепи реактивную мощность можно измерить с помощью двух однофазных счетчиков. Для этого их включают в цепь, как и ваттметры, по схеме (рис.5). Реактивная энергия равна разности показаний счетчиков, умноженной на
Похожие статьи:poznayka.org Трехфазные электрические цепи | Kursak.NETТрехфазные электрические цепи Основные понятия и определения Трехфазная цепь является частным случаем многофазных систем электрических цепей, представляющих собой совокупность электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой и создаваемые общим источником энергии. Каждую из частей многофазной системы, характеризующуюся одинаковым током, принято называть фазой. Таким образом, понятие "фаза" имеет в электротехнике два значения: первое – аргумент синусоидально изменяющейся величины, второе – часть многофазной системы электрических цепей. Цепи в зависимости от количества фаз называют двухфазными, трехфазными, шестифазными и т.п. Трехфазные цепи – наиболее распространенные в современной электроэнергетике. Это объясняется рядом их преимуществ по сравнению как с однофазными, так и с другими многофазными цепями: · экономичность производства и передачи энергии по сравнению с однофазными цепями; · возможность сравнительно простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя; · возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного. Трехфазная цепь состоит из трех основных элементов: трехфазного генератора, в котором механическая энергия преобразуется в электрическую с трехфазной системой ЭДС; линии передачи со всем необходимым оборудованием; приемников (потребителей), которые могут быть как трехфазными (например, трехфазные асинхронные двигатели), так и однофазными (например, лампы накаливания). Трехфазный генератор представляет собой синхронную машину двух типов: турбогенератор и гидрогенератор. Модель трехфазного генератора схематически изображена на рис. 3.1.
Рис. 3.1 На статоре 1 генератора размещается обмотка 2, состоящая из трех частей или, как их принято называть, фаз. Обмотки фаз располагаются на статоре таким образом, чтобы их магнитные оси были сдвинуты в пространстве относительно друг друга на угол 2π/3, т.е. на 120°. На рис. 3.1 каждая фаза обмотки статора условно показана состоящей из одного витка. Начала фаз обозначены буквами A, B и C, а концы – X, Y, Z. Ротор 3 представляет собой электромагнит, возбуждаемый постоянным током обмотки возбуждения 4, расположенной на роторе. При вращении ротора турбиной с равномерной скоростью в обмотках фаз статора индуктируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся друг от друга по фазе на 120° вследствие их пространственного смещения. На схеме обмотку (или фазу) источника питания изображают как показано на рис. 3.2. За условное положительное направление ЭДС в каждой фазе принимают направление от конца к началу. Обычно индуктированные в обмотках статора ЭДС имеют одинаковые амплитуды и сдвинуты по фазе относительно друг друга на один и тот же угол 120°. Такая система ЭДС называется симметричной.
Рис. 3.2 Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями комплексного переменного. Графики мгновенных значений трехфазной симметричной системы ЭДС показаны на рис. 3.3. Если ЭДС одной фазы (например, фазы A) принять за исходную и считать её начальную фазу равной нулю, то выражения мгновенных значений ЭДС можно записать в виде (3.1) eA=Emsinωt, eB=Emsin(ωt−120°), eC=Emsin(ωt−240°)=Emsin(ωt+120°).
Из графика мгновенных значений (рис 3.3) следует (3.2) eA+eB+eC=0 Комплексные действующие ЭДС будут иметь выражения: (3.3) ĖA=Emej0°=Em(1+j0), ĖB=Eme−j120°=Em(−1/2−j Векторная диаграмма трехфазной симметричной системы ЭДС показана на рис 3.4а.
Рис. 3.4 На диаграмме рис. 3.4а вектор ĖA направлен вертикально, так как при расчете трехфазных цепей принято направлять вертикально вверх ось действительных величин. Из векторных диаграмм рис 3.4 следует, что для симметричной трехфазной системы геометрическая сумма векторов ЭДС всех фаз равна нулю: (3.4) ĖA+ĖB+ĖC=0. Систему ЭДС, в которой ЭДС фазы B отстает по фазе от ЭДС фазы A, а ЭДС фазы C по фазе – от ЭДС фазы B, называют системой прямой последовательности. Если изменить направление вращения ротора генератора, то последовательность фаз изменится (рис. 3.4б) и будет называться обратной. Последовательность фаз определяет направление вращения трехфазных двигателей. Для определения последовательности фаз имеются специальные приборы – фазоуказатели. В период зарождения трехфазных систем имелись попытки использовать несвязанную систему, в которой фазы обмотки генератора не были электрически соединены между собой и каждая фаза соединялась со своим приемником двумя проводами (рис. 3.5). Такие системы не получили применения вследствие их неэкономичности: для соединения генератора с приемником требовалось шесть проводов (рис. 3.5)
Рис. 3.5 Более совершенными и экономичными являются связанные цепи, в которых фазы обмотки электрически соединены между собой. Существуют различные способы соединения фаз трехфазных источников питания и трехфазных потребителей электроэнергии. Наиболее распространенными являются соединения "звезда" и "треугольник". При этом способ соединения фаз источников и фаз потребителей в трехфазных системах могут быть различными. Фазы источника обычно соединены "звездой", фазы потребителей соединяются либо "звездой", либо "треугольником". Соединение фаз генератора и приемника звездой При соединение фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников (Za, Zb, Zc) также соединяют в одну точку n. Такое соединение называется соединение звезда.
Рис. 3.6 Провода A−a, B−b и C−c, соединяющие начала фаз генератора и приемника, называются линейными, провод N−n, соединяющий точку N генератора с точкой n приемника, – нейтральным. Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной. В трехфазных цепях различают фазные и линейные напряжения. Фазное напряжение UФ – напряжение между началом и концом фазы или между линейным проводом и нейтралью (UA, UB, UC у источника; Ua, Ub, Uc у приемника). Если сопротивлением проводов можно пренебречь, то фазное напряжение в приемнике считают таким же, как и в источнике. (UA=Ua, UB=Ub, UC=Uc). За условно положительные направления фазных напряжений принимают направления от начала к концу фаз. Линейное напряжение (UЛ) – напряжение между линейными проводами или между одноименными выводами разных фаз (UAB, UBC, UCA). Условно положительные направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу (рис. 3.6). По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи: · Фазные (IФ) – это токи в фазах генератора и приемников. · Линейные (IЛ) – токи в линейных проводах. При соединении в звезду фазные и линейные токи равны (3.5) IФ=IЛ. Ток, протекающий в нейтральном проводе, обозначают IN. По первому закону Кирхгофа для нейтральной точки n (N) имеем в комплексной форме (3.6) İN=İA+İB+İC.
Рис. 3.7 В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа. (3.7) ÚAB=ÚA−ÚB; ÚBC=ÚB−ÚC; ÚCA=ÚC−ÚA. Согласно этим выражениям на рис. 3.7а построена векторная диаграмма, из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: UAB, UBC, UCA равны по величине и сдвинуты по фазе относительно друг друга на 120° (общее обозначение UЛ), и опережают, соответственно, векторы фазных напряжений UA, UB, UC, (UФ) на угол 30°. Действующие значения линейных напряжений можно определить графи-чески по векторной диаграмме или по формуле (3.8), которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений: UЛ=2UФcos30° или (3.8) UЛ= Предусмотренные ГОСТом линейные и фазные напряжения для цепей низкого напряжения связаны между собой соотношениями: UЛ=660В;UФ=380В; UЛ=380В;UФ=220В; UЛ=220В;UФ=127В. Векторную диаграмму удобно выполнить топографической (рис. 3.7б), тогда каждой точке цепи соответствует определенная точка на диаграмме. Вектор, проведенный между двумя точками топографической диаграммы, выражает по величине и фазе напряжения между одноименными точками цепи. Классификация приемников в трехфазной цепи Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными. К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т.д. К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Обычно комплексные сопротивления фаз трехфазных приемников равны между собой: (3.9) Za = Zb = Zc = Zejφ. Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным. Четырехпроводная цепь Для расчета трехфазной цепи применимы все методы, используемые для расчета линейных цепей. Обычно сопротивления проводов и внутреннее сопротивление генератора меньше сопротивлений приемников, поэтому для упрощения расчетов таких цепей (если не требуется большая точность) сопротивления проводов можно не учитывать (ZЛ = 0, ZN = 0). Тогда фазные напряжения приемника Ua, Ub и Uc будут равны соответственно фазным напряжениям источника электрической энергии(генератора или вторичной обмотки трансформатора), т.е. Ua = UA; Ub = UB; Uc = UC. Если полные комплексные сопротивления фаз приемника равны Za = Zb = Zc, то токи в каждой фазе можно определить по формулам (3.10) İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc. В соответствии с первым законом Кирхгофа ток в нейтральном проводе (3.11) İN = İa + İb + İc = İA + İB + İC. Симметричная нагрузка приемника При симметричной системе напряжений и симметричной нагрузке, когда Za = Zb = Zc, т.е. когда Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны по значению и углы сдвига фаз одинаковы (3.12) Ia = Ib = Ic = Iф = Uф / Zф, (3.13) φa = φb = φc = φ = arctg (Xф/Rф). Построив векторную диаграмму токов для симметричного приемника (рис. 3.8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.
Рис. 3.8 Несимметричная нагрузка приемника При симметричной системе напряжений и несимметричной нагрузке, когда Za ≠ Zb ≠ Zc и φa ≠ φb ≠ φc токи в фазах потребителя различны и определяются по закону Ома İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc. Ток в нейтральном проводе İN равен геометрической сумме фазных токов İN = İa + İb + İc. Напряжения будут Ua = UA; Ub = UB; Uc = UC, UФ = UЛ / Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке. Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз. Векторная диаграмма при несимметричной нагрузке приведена на рис. 3.9
Рис. 3.9 Трехпроводная электрическая цепь Схема соединения источника и приемника звездой без нейтрального провода приведена на рис. 3.10.
Рис. 3.10 При симметричной нагрузке, когда Za = Zb = Zc = Zφ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, UnN = 0. Соотношение между фазными и линейными напряжениями приемника также равно При несимметричной нагрузке Za ≠ Zb ≠ Zc между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтрали UnN. Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3.10 представляет собой схему с двумя узлами, (3.14)
где: Ya = 1 / Za; Yb = 1 / Zb; Yc = 1 / Zc – комплексы проводимостей фаз нагрузки. Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что (3.15) Úa = ÚA – ÚnN; Úb = ÚB – ÚnN; Úc = ÚC – ÚnN. Зная фазные напряжения приемника, можно определить фазные токи: (3.16) İa = Úa / Za = Ya Úa; İb = Úb / Zb = Yb Úb; İc = Úc / Zc = Yc Úc. Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и UnN (рис. 3.11). При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали UnN может изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Úa, Úb и Úc могут отличаться друг от друга весьма существенно. Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Úa, Úb, Úc и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).
Рис. 3.11 Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки. Поэтому нейтральный провод необходим для того, чтобы: · выравнивать фазные напряжения приемника при несимметричной нагрузке; · подключать к трехфазной цепи однофазные приемники с номинальным напряжением в Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки. Соединение фаз генератора и приемника треугольником При соединении источника питания треугольником (рис. 3.12) конец X одной фазы соединяется с началом В второй фазы, конец Y второй фазы – с началом С третьей фазы, конец третьей фазы Z – c началом первой фазы А. Начала А, В и С фаз подключаются с помощью трех проводов к приемникам.
Рис. 3.12 Соединение фаз источника в замкнутый треугольник возможно при симметричной системе ЭДС, так как (3.17) ĖA + ĖB + ĖC = 0. Если соединение обмоток треугольником выполнено неправильно, т.е. в одну точку соединены концы или начала двух фаз, то суммарная ЭДС в контуре треугольника отличается от нуля и по обмоткам протекает большой ток. Это аварийный режим для источников питания, и поэтому недопустим. Напряжение между концом и началом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению. (3.18) UЛ = UФ. Пренебрегая сопротивлением линейных проводов, линейные напряжения потребителя можно приравнять линейным напряжениям источника питания: Uab = UAB, Ubc = UBC, Uca = UCA. По фазам Zab, Zbc, Zca приемника протекают фазные токи İab, İbc и İca. Условное положительное направление фазных напряжений Úab, Úbc и Úca совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов İA, İB и İC принято от источников питания к приемнику. В отличие от соединения звездой при соединении треугольником фазные токи не равны линейным. Токи в фазах приемника определяются по формулам (3.19) İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca. Линейные токи можно определить по фазным, составив уравнения по первому закону Кирхгофа для узлов a, b и c (рис 3.12) (3.20) İA = İab – İca; İB = İbc – İab; İC = İca – İbc. Сложив левые и правые части системы уравнений, (3.20), получим (3.21) İA + İB + İC = 0, т.е. сумма комплексов линейных токов равна нулю как при симметричной, так и при несимметричной нагрузке. Симметричная нагрузка При симметричной нагрузке (3.22) Zab = Zbc = Zca = Zejφ, т.е. Zab = Zbc = Zca = Z, φab = φbc = φca = φ. Так как линейные (они же фазные) напряжения UAB, UBC, UCA симметричны, то и фазные токи образуют симметричную систему İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca. Абсолютные значения их равны, а сдвиги по фазе относительно друг друга составляют 120°. Линейные токи İA = İab – İca; İB = İbc – İab; İC = İca – İbc; образуют также симметричную систему токов (рис.3.13, 3.14).
Рис. 3.13 На векторной диаграмме (рис. 3.14) фазные токи отстают от фазных напряжений на угол φ (полагаем, что фазы приемника являются индуктивными, т.е. φ > 0°). Здесь принято, что напряжение UAB имеет нулевую фазу. Из диаграммы следует, что любой линейный ток больше фазного в Таким образом, при соединении треугольником действующее значение линейного тока при симметричной нагрузке в При равномерной нагрузке фаз расчет трехфазной цепи соединенной треугольником, можно свести к расчету одной фазы. Фазное напряжение UФ = UЛ. Фазный ток IФ = UФ / ZФ, линейный ток IЛ =
Рис. 3.14 Несимметричная нагрузка приемника В общем случае при несимметричной нагрузке Zab ≠ Zbc ≠ Zca. Обычно она возникает при питании от трехфазной сети однофазных приемников. Например, для нагрузки, рис. 3.15, фазные токи, углы сдвига фаз и фазные мощности будут в общем случае различными.
Рис. 3.15 Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bc – активно-индуктивная, а в фазе ca – активно-емкостная приведена на рис. 3.16, топографическая диаграмма – на рис. 3.17.
Рис. 3.16 Построение векторов линейных токов произведено в соответствии с выражениями İA = İab – İca; İB = İbc – İab; İC = İca – İbc.
Рис. 3.17 Таким образом, при несимметричной нагрузке симметрия фазных токов İab, İbс, İca нарушается, поэтому линейные токи İA, İB, İC можно определить только расчетом по вышеприведенным уравнениям (3.20) или найти графическим путем из векторных диаграмм (рис. 3.16, 3.17). Важной особенностью соединения фаз приемника треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным, так как линейные напряжения генератора являются постоянными. Будет изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой. Поэтому схема соединения треугольником широко используется для включения несимметричной нагрузки. При расчете для несимметричной нагрузки сначала определяют значения фазных токов İab, İbc, İca и соответствующие им сдвиги фаз φab, φbc, φca. Затем определяют линейные токи с помощью уравнений (3.20) в комплексной форме или с помощью векторных диаграмм (рис. 3.16, 3.17). Общие замечания к расчету трехфазных цепей 1. При расчете трехфазных цепей исходят из предположения, что генератор дает симметричную систему напряжений. На практике несимметрия нагрузки практически не влияет на систему напряжений генератора в том случае, если мощность нагрузки мала по сравнению с мощностью генератора или сети электроснабжения. 2. Схема соединения обмоток трехфазного генератора не предопределяет схему соединения нагрузки. Так, при соединении фаз генератора в звезду нагрузка может быть соединена в звезду с нейтральным проводом, в звезду без нейтрального провода или, наконец, в треугольник. Мощность трехфазной цепи, ее расчет и измерение В трехфазных цепях, так же как и в однофазных, пользуются понятиями активной, реактивной и полной мощностей. Соединение потребителей звездой В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз (3.23) P = Pa + Pb + Pc, где (3.24) Pa = Ua Ia cos φa; Pb = Ub Ib cos φb; Pc = Uc Ic cos φc; Ua, Ub, Uc; Ia, Ib, Ic – фазные напряжения и токи; φa, φb, φc – углы сдвига фаз между напряжением и током. Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз (3.25) Q = Qa + Qb + Qc, где (3.26) Qa = Ua Ia sin φa; Qb = Ub Ib sin φb; Qc = Uc Ic sin φc. Полная мощность отдельных фаз (3.27) Sa = Ua Ia; Sb = Ub Ib; Sc = Uc Ic. Полная мощность трехфазного приемника (3.28)
При симметричной системе напряжений (Ua = Ub = Uc = UФ) и симметричной нагрузке (Ia = Ib = Ic = IФ; φa = φb = φc = φ) фазные мощности равны Pa = Pb = Pc = PФ = UФ IФ cos φ; Qa = Qb = Qc = QФ = UФ IФ sin φ. Активная мощность симметричного трехфазного приемника (3.29) P = 3 PФ = 3 UФ IФ cos φ. Аналогично выражается и реактивная мощность (3.30) Q = 3 QФ = 3 UФ IФ sin φ. Полная мощность (3.31) S = 3 SФ = 3 UФ IФ. Отсюда следует, что в трехфазной цепи при симметричной системе напряжений и симметричной нагрузке достаточно измерить мощность одной фазы и утроить результат. Соединение потребителей треугольником В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз (3.32) P = Pab + Pbc + Pca, где (3.33) Pab = Uab Iab cos φab; Pbc = Ubc Ibc cos φbc; Pca = Uca Ica cos φca; Uab, Ubc, Uca; Iab, Ibc, Ica – фазные напряжения и токи; φab, φbc, φca – углы сдвига фаз между напряжением и током. Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз (3.34) Q = Qab + Qbc + Qca, где (3.35) Qab = Uab Iab sin φab; Qbc = Ubc Ibc sin φbc; Qca = Uca Ica sin φca. Полная мощность отдельных фаз (3.36) Sab = Uab Iab; Sbc = Ubc Ibc; Sca = Uca Ica. Полная мощность трехфазного приемника (3.37)
При симметричной системе напряжений (Uab = Ubc = Uca = UФ) и симметричной нагрузке (Iab = Ibc = Ica = IФ; φab = φbc = φca = φ) фазные мощности равны Pab = Pbc = Pca = PФ = UФ IФ cos φ; Qab = Qbc = Qca = QФ = UФ IФ sin φ. Активная мощность симметричного трехфазного приемника P = 3 PФ = 3 UФ IФ cos φ. Аналогично выражается и реактивная мощность Q = 3 QФ = 3 UФ IФ sin φ. Полная мощность S = 3 SФ = 3 UФ IФ. Так как за номинальные величины обычно принимают линейные напряжения и токи, то мощности удобней выражать через линейные величины UЛ и IЛ. При соединении фаз симметричного приемника звездой UФ = UЛ / (3.38) P = где UЛ и IЛ – линейное напряжение и ток; cos φ – фазный. Обычно индексы "л" и "ф" не указывают и формула принимает вид (3.39) P = Соответственно реактивная мощность (3.40) Q = и полная мощность (3.41) S = При этом надо помнить, что угол φ является углом сдвига фаз между фазными напряжением и током, и, что при неизмененном линейном напряжении, переключая приемник со звезды в треугольник его мощность увеличивается в три раза: Δ P = Υ 3P. Измерение активной мощности в трехфазных цепях Измерение активной мощности в трехфазных цепях производят с помощью трех, двух или одного ваттметров, используя различные схемы их включения. Схема включения ваттметров для измерения активной мощности определяется схемой сети (трех- или четырехпроводная), схемой соединения фаз приемника (звезда или треугольник), характером нагрузки (симметричная или несимметричная), доступностью нейтральной точки. При несимметричной нагрузке в четырехпроводной цепи активную мощность измеряют тремя ваттметрами (рис. 3.18), каждый из которых измеряет мощность одной фазы – фазную мощность.
Рис. 3.18 Активная мощность приемника определяют по сумме показаний трех ваттметров (3.42) P = P1 + P2 + P3, где P1 = UA IA cos φA; P2 = UB IB cos φB; P3 = UC IC cos φC. Измерение мощности тремя ваттметрами возможно при любых условиях. При симметричном приемнике и доступной нейтральной точке активную мощность приемника определяют с помощью одного ваттметра, измеряя активную мощность одной фазы PФ по схеме рис. 3.19. Активная мощность всего трехфазного приемника равна при этом утроенному показанию ваттметра: P = 3 PФ.
Рис. 3.19
Рис. 3.20 На рис. 3.19 показано включение прибора непосредственно в одну из фаз приемника. В случае, если нейтральная точка приемника недоступна или зажимы фаз приемника, включенного треугольником не выведены, применяют схему рис. 3.20 с использованием искусственной нейтральной точки n’. В этой схеме дополнительно в две фазы включают резисторы с сопротивлением R = RV. Измерение активной мощности симметричного приемника в трехфазной цепи одним ваттметром применяют только при полной гарантии симметричности трехфазной системы. Измерение активной мощности двумя ваттметрами В трехпроводных трехфазных цепях при симметричной и несимметричной нагрузках и любом способе соединения приемников широко распространена схема измерения активной мощности приемника двумя ваттметрами (рис. 3.21). Показания двух ваттметров при определенной схеме их включения позволяют определить активную мощность трехфазного приемника, включенного в цепь с симметричным напряжением источника питания. На рис. 3.21 показана одна из возможных схем включения ваттметров: здесь токовые катушки включены в линейные провода с токами IA и IB, а катушки напряжения – соответственно на линейные напряжения UAC и UBC.
Рис. 3.21 Докажем, что сумма показаний ваттметров, включенных по схеме рис. 3.21, равна активной мощности Р трехфазного приемника. Мгновенное значение общей мощности трехфазного приемника, соединенного звездой, (3.43) p = uA iA + uB iB + uC iC. Так как (3.44) iA + iB + iC = 0. то (3.45) iC = -(iA + iB). Подставляя значение iC в выражение для р, получаем (3.46) p = uA iA + uB iB – uC (iA + iB) = (uA – uC) iA + (uB – uC) iB = uAC iA + uBC iB. Выразив мгновенные значения u и i через их амплитуды, можно найти среднюю (активную) мощность (3.47)
которая составит (3.48) P = UAC IA cos(UAC^IA) + UBC IB cos(UBC^IB) = P1 + P2. Так как UAC, UBC, IA и IB – соответственно линейные напряжения и токи, то полученное выражение справедливо и при соединении потребителей треугольником. Следовательно, сумма показаний двух ваттметров действительно равна активной мощности Р трехфазного приемника. При симметричной нагрузке IA = IB = IЛ, UAC = UBC = UЛ.
Рис. 3.22 Из векторной диаграммы (рис. 3.22) получаем, что угол α между векторами UAC и IA равен α = φ – 30°, а угол β между векторами UBC и IB составляет β = φ + 30°. В рассматриваемом случае показания ваттметров можно выразить формулами (3.49) P1 = UЛ IЛ cos(φ – 30°), (3.50) P2 = UЛ IЛ cos(φ + 30°). Сумма показаний ваттметров (3.51) P1 + P2 = UЛ IЛ [cos(φ – 30°) + cos(φ + 30°)] = Ввиду того, что косинусы углов в полученной формуле могут быть как положительными, так и отрицательными, в общем случае активная мощность приемника, измеренная по методу двух ваттметров, равна алгебраической сумме показаний. При симметричном приемнике показания ваттметров Р1 и Р2 будут равны только при φ = 0°. Если φ > 60°, то показания второго ваттметра Р2 будет отрицательным. Для измерения активной мощности в трехфазных цепях промышленных установок широкое применение находят двухэлементные трехфазные электродинамические и ферродинамические ваттметры, которые содержат в одном корпусе два измерительных механизма и общую подвижную часть. Катушки обоих механизмов соединены между собой по схемам, соответствующим рассмотренному методу двух ваттметров. Показание двухэлементного ваттметра равно активной мощности трехфазного приемника.
kursak.net | ||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|




 ; для схемы соединения "треугольником"
; для схемы соединения "треугольником"  . Активная мощность фазы потребителя
. Активная мощность фазы потребителя
 , для "треугольника":
, для "треугольника":  .
. 

 ,
, .
.
 , поэтому
, поэтому
 ; мощности - совпадают с формулой
; мощности - совпадают с формулой
 , то
, то 



 .
.
 нагрузки (двигатели имеют
нагрузки (двигатели имеют  0,5 и 0,85), параллельно потребителю включена батарея конденсаторов ( по 160 мкФ в каждой фазе). Наличие двух уровней напряжений в зависимости от включения потребителя дает возможность включать без трансформатора потребители с разными номинальными напряжениями: к трехпроводной линии с напряжением UЛ = 220 В по схеме "звезда" подключим двигатель с номинальными напряжениями (220/380) В. Осветительная нагрузка равномерно распределяется между фазами А, В, С и включена по схеме "треугольник" на номинальное напряжение 220 В. Три батареи конденсаторов включены по схеме "треугольник", что дает возможность, в сравнении со схемой "звезда", при той же самой реактивной мощности конденсаторов QC втрое уменьшить емкость. Из выражений
0,5 и 0,85), параллельно потребителю включена батарея конденсаторов ( по 160 мкФ в каждой фазе). Наличие двух уровней напряжений в зависимости от включения потребителя дает возможность включать без трансформатора потребители с разными номинальными напряжениями: к трехпроводной линии с напряжением UЛ = 220 В по схеме "звезда" подключим двигатель с номинальными напряжениями (220/380) В. Осветительная нагрузка равномерно распределяется между фазами А, В, С и включена по схеме "треугольник" на номинальное напряжение 220 В. Три батареи конденсаторов включены по схеме "треугольник", что дает возможность, в сравнении со схемой "звезда", при той же самой реактивной мощности конденсаторов QC втрое уменьшить емкость. Из выражений
 .
.
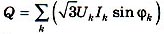
 всех потребителей без батарей емкостей.
всех потребителей без батарей емкостей.  до компенсации:
до компенсации:
 по формуле определяется емкость для каждой батареи:
по формуле определяется емкость для каждой батареи:
 эл. рад. На рис. 1 каждая фаза
статора условно показана в виде одного витка. Начала обмоток принято обозначать
заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в
неподвижных обмотках статора индуцируются в результате пересечения их витков
магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора
(на рис. 1 ротор условно изображен в виде постоянного магнита, что используется
на практике при относительно небольших мощностях). При вращении ротора с равномерной
скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные
ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного
сдвига друг от друга по фазе на
эл. рад. На рис. 1 каждая фаза
статора условно показана в виде одного витка. Начала обмоток принято обозначать
заглавными буквами А,В,С, а концы- соответственно прописными x,y,z. ЭДС в
неподвижных обмотках статора индуцируются в результате пересечения их витков
магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора
(на рис. 1 ротор условно изображен в виде постоянного магнита, что используется
на практике при относительно небольших мощностях). При вращении ротора с равномерной
скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные
ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного
сдвига друг от друга по фазе на  рад. (см. рис. 2).
рад. (см. рис. 2).  . В частности векторная диаграмма для симметричной
системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена
на рис. 3.
. В частности векторная диаграмма для симметричной
системы ЭДС, соответствующей трехфазной системе синусоид на рис. 2, представлена
на рис. 3.


 и
и  равны соответствующим фазным токам.
При наличии нейтрального провода ток в нейтральном проводе
равны соответствующим фазным токам.
При наличии нейтрального провода ток в нейтральном проводе  . Если система фазных токов симметрична,
то
. Если система фазных токов симметрична,
то  . Следовательно, если бы симметрия
токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано
далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке
при несимметрии самой нагрузки.
. Следовательно, если бы симметрия
токов была гарантирована, то нейтральный провод был бы не нужен. Как будет показано
далее, нейтральный провод обеспечивает поддержание симметрии напряжений на нагрузке
при несимметрии самой нагрузки. - фазные напряжения нагрузки.
- фазные напряжения нагрузки. ;
; ;
; .
.
 - как сумма напряжений по замкнутому контуру.
- как сумма напряжений по замкнутому контуру.
 . Тогда для случая прямого чередования
фаз
. Тогда для случая прямого чередования
фаз  ,
,  (при обратном чередовании фаз
фазовые сдвиги у
(при обратном чередовании фаз
фазовые сдвиги у  и
и  меняются местами). С учетом этого
на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений.
Однако при симметрии напряжений эти величины легко определяются непосредственно
из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат
по вектору
меняются местами). С учетом этого
на основании соотношений (1) …(3) могут быть определены комплексы линейных напряжений.
Однако при симметрии напряжений эти величины легко определяются непосредственно
из векторной диаграммы на рис. 7. Направляя вещественную ось системы координат
по вектору  (его начальная фаза равна нулю),
отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их
модули определяем в соответствии с (4). Так для линейных напряжений
(его начальная фаза равна нулю),
отсчитываем фазовые сдвиги линейных напряжений по отношению к этой оси, а их
модули определяем в соответствии с (4). Так для линейных напряжений  и
и  получаем:
получаем:  ;
;  .
.  .
. и в треугольнике будет протекать
ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать
порядок соединения фаз: начало одной фазы соединяется с концом другой.
и в треугольнике будет протекать
ток короткого замыкания. Следовательно, для треугольника нужно строго соблюдать
порядок соединения фаз: начало одной фазы соединяется с концом другой.


 .
. . Определить комплексы остальных
фазных и линейных токов.
. Определить комплексы остальных
фазных и линейных токов.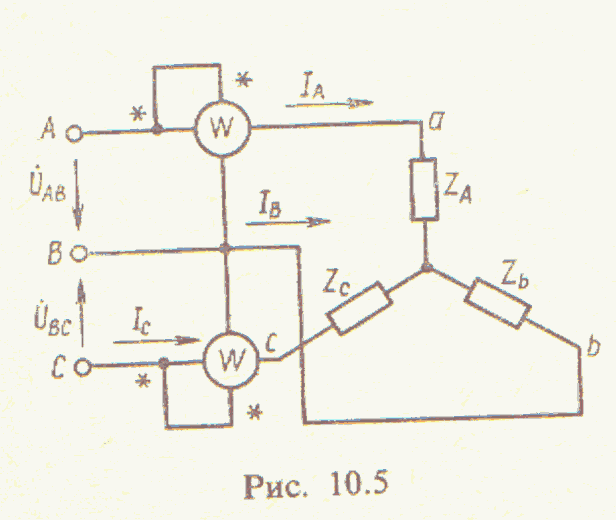

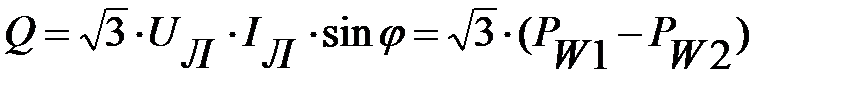


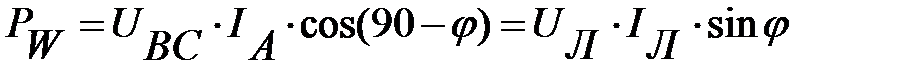
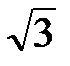 .
.



 /2), ĖC=Eme+j120°=Em(−1/2+j
/2), ĖC=Eme+j120°=Em(−1/2+j![clip_image004[1] clip_image004[1]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0041_thumb16.gif) /2).
/2).



![clip_image004[2] clip_image004[2]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0042_thumb11.gif) UФ.
UФ.
![clip_image004[3] clip_image004[3]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0043_thumb8.gif) , благодаря нейтральному проводу при ZN = 0.
, благодаря нейтральному проводу при ZN = 0.

![clip_image004[4] clip_image004[4]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0044_thumb4.gif) , т.е. UФ = UЛ /
, т.е. UФ = UЛ / ![clip_image004[5] clip_image004[5]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0045_thumb3.gif) , а токи в фазах определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением φ = arctg (X / R).
, а токи в фазах определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением φ = arctg (X / R). ,
,
![clip_image004[6] clip_image004[6]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0046_thumb3.gif) раз меньше номинального линейного напряжения сети.
раз меньше номинального линейного напряжения сети.

![clip_image004[7] clip_image004[7]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0047_thumb2.gif) раз. Линейный ток İA отстает по фазе от фазного тока İab на угол 30°, на этот же угол отстает İB от İbc, İC от İca.
раз. Линейный ток İA отстает по фазе от фазного тока İab на угол 30°, на этот же угол отстает İB от İbc, İC от İca.![clip_image004[8] clip_image004[8]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0048_thumb2.gif) раз больше действующего значения фазного тока и UЛ = UФ; IЛ =
раз больше действующего значения фазного тока и UЛ = UФ; IЛ =![clip_image004[9] clip_image004[9]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0049_thumb2.gif) IФ.
IФ.![clip_image004[10] clip_image004[10]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image00410_thumb2.gif) IФ, угол сдвига по фазе φ = arctg (XФ / RФ).
IФ, угол сдвига по фазе φ = arctg (XФ / RФ).



 .
.![clip_image020[1] clip_image020[1]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image0201_thumb10.gif) .
.![clip_image004[11] clip_image004[11]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image00411_thumb2.gif) , IФ = IЛ, при соединении треугольником UФ = UЛ, IФ = IЛ /
, IФ = IЛ, при соединении треугольником UФ = UЛ, IФ = IЛ / ![clip_image004[12] clip_image004[12]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image00412_thumb2.gif) . Поэтому независимо от схемы соединения фаз приемника активная мощность при симметричной нагрузке определяется одной и той же формулой
. Поэтому независимо от схемы соединения фаз приемника активная мощность при симметричной нагрузке определяется одной и той же формулой![clip_image004[13] clip_image004[13]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image00413_thumb2.gif) UЛ IЛ cos φ.
UЛ IЛ cos φ.![clip_image004[14] clip_image004[14]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image00414_thumb2.gif) U I cos φ.
U I cos φ.![clip_image004[15] clip_image004[15]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image00415_thumb.gif) U I sin φ.
U I sin φ.![clip_image004[16] clip_image004[16]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image00416_thumb.gif) U I.
U I.



 ,
,
![clip_image004[17] clip_image004[17]](/800/600/http/kursak.net/wp-content/uploads/2015/04/clip_image00417_thumb.gif) UЛ IЛ cos φ.
UЛ IЛ cos φ.












