3.2 Выбор числа и мощности трансформаторов цтп с учетом компенсации реактивной мощности. Косинус фи трансформатора. Косинус фи для электродвигателей таблицаПростыми словами о коэффициенте мощности (косинусе фи)Дата публикации: 23 августа 2018. Допустим, вы купили компрессор для полива растений или электродвигатель для циркулярной пилы. В инструкции по эксплуатации помимо основных технических характеристик (таких, как потребляемый ток, рабочее напряжение, частота вращения) вы можете обнаружить такой непонятный показатель, как косинус фи (cos ϕ). Данная информация может быть указана и на пластинке (шильдике), закрепленной на корпусе прибора. В нашей статье мы постараемся объяснить простым и доступным языком всем, даже пользователям далеким от электротехнических тонкостей, как тригонометрическая функция (знакомая нам со школьной скамьи) влияет на работу всем нам привычных электробытовых приборов, и почему ее называют коэффициентом мощности.
Важно! Все нижесказанное касается только сетей переменного тока. Далекий от электротехники, но весьма наглядный примерЧтобы объяснить, каким образом угол ϕ (а точнее его косинус) влияет на мощность, рассмотрим пример, не имеющий никакого отношения к электротехнике. Допустим нам необходимо передвинуть тележку, стоящую на рельсах. Чтобы удобнее было производить данную операцию, к ее передней части прикрепляем канат.
Если мы будем тянуть за веревку прямо вперед по направлению движения, то для перемещения тележки нам понадобится приложить достаточно небольшое усилие. Однако если находиться сбоку от рельсов и тянуть за канат в сторону, то для движения тележки с такой же скоростью необходимо будет приложить значительно большее усилие. Причем чем больше угол (ϕ) между направлением движения и прикладываемым усилием, тем больше «мощности» потребуется от нас.  Вывод! То есть, увеличение угла ϕ ведет к увеличению расходуемой нами энергии (при одной и той же выполненной работе). Сдвиг фаз между напряжением и токомПри использовании энергии переменного тока происходит приблизительно то же самое. При активной нагрузке (например, при включении электрочайника или лампы накаливания) переменные напряжение (U) и ток (I) полностью совпадают по фазе и одновременно достигают своих максимальных значений. В данном случае мощность потребителя электроэнергии можно рассчитать по формуле P=U•I.
Для сети переменного тока работающий электродвигатель, имеющийся, например, в стиральной машине, является комплексной нагрузкой, включающей в себя активную и индуктивную составляющие. При подаче напряжения на такой прибор оно появляется на обмотках, практически, мгновенно. А вот ток (из-за влияния индуктивности) запаздывает. То есть между ними образуется так называемый сдвиг фаз, который мы и называем ϕ.
При активно-емкостной нагрузке, наоборот, переменный ток сразу начинает течь через конденсатор, а напряжение отстает от него по фазе на величину ϕ.
Треугольник мощностейКоэффициент мощности (PF) – это отношение мощностей: активной полезной (P) к полной (S). Чтобы показать, каким образом сдвиг фаз влияет на PF, используем так называемый треугольник мощностей. И вот тут-то нам и потребуются минимальные знания школьной тригонометрии.
Из теории о прямоугольных треугольниках всем нам известно, что cos ϕ=P/S. То есть, косинус фи - это и есть коэффициент мощности (PF), который показывает, какая часть от полной мощности (S= U•I) фактически необходима для конкретной нагрузки. Чем больше реактивная составляющая Q, тем меньше полезная P. Чтобы вычислить активную мощность необходимо полную S умножить на косинус фи: P= S•cos ϕ. На заметку! Считать косинус фи абсолютным аналогом коэффициента мощности можно только при том условии, что мы имеем в электрической сети идеальную синусоиду. Для более точного расчета необходимо учитывать нелинейные искажения, которые имеют переменные напряжение и ток. На практике, зачастую коэффициентом нелинейных искажений синусоиды пренебрегают, и значение косинуса фи принимают за приближенное значение коэффициента мощности. Усредненные значения коэффициента мощностиЛампы накаливания и электрические нагревательные элементы, хотя и имеют в своих конструкциях спирали, намотанные с помощью специального провода, считаются чисто активной нагрузкой для сетей переменного тока. Так как индуктивность этих элементов настолько мала, что ею, как правило, просто пренебрегают. Для таких приборов cos ϕ (или коэффициент мощности) принимают равным 1. В разнообразных электрических ручных инструментах (дрелях, перфораторах, лобзиках и так далее) индуктивная составляющая мощности достаточно мала. Для них принято считать cos ϕ≈0,96÷0,97. Этот показатель достаточно близок к единице, поэтому его, практически, никогда не указывают в технических характеристиках. Для мощных электродвигателей, люминесцентных ламп и сварочных трансформаторов cos ϕ≈0,5÷0,82. Этот коэффициент мощности необходимо учитывать, например, при выборе диаметра питающих проводов, чтобы они не нагрелись, и не сгорела их изоляция.
На что влияет низкий коэффициент мощностиК чему могут привести низкие показатели коэффициента мощности:
В заключенииСмело можно утверждать, что чем ближе значение PF к единице, тем эффективнее используется электроэнергия. В некоторых мощных приборах производители устанавливают специальные приспособления, которые позволяют осуществлять коррекцию коэффициента мощности.
Компенсация реактивной мощности асинхронных двигателейВ таблице, приведенной ниже, представлены значения, мощности косинусного (фазового) конденсатора, подключаемого к клеммам асинхронного двигателя, для компенсации реактивной мощности без самовозбуждения. В любом случае необходимы измерения, чтобы максимальный ток текущий через конденсатор не превышал 90%, тока холостого хода двигателя.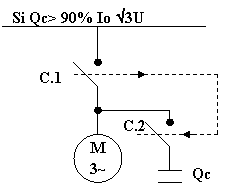 
Однако, если мощность конденсатора больше чем величины, обозначенные в вышеупомянутой таблице или если: Qc> 90% Io √3U, то местная компенсация реактивной мощности двигателя возможна. Необходимо добавить контактор (C.2) в схему управления двигателем. Контакторы (С.1) (С.2) включаются одновременно. Зависимость между мощностью конденсатора в кВАр и емкостью в мкФ
НИЗКОВОЛЬТНЫЕ ДВИГАТЕЛИ 0,4 кВ
ВЫСОКОВОЛЬТНЫЕ ДВИГАТЕЛИ 6-10 кВ
www.matic.ru Простыми словами о коэффициенте мощности (косинусе фи)Дата публикации: 23 августа 2018. Допустим, вы купили компрессор для полива растений или электродвигатель для циркулярной пилы. В инструкции по эксплуатации помимо основных технических характеристик (таких, как потребляемый ток, рабочее напряжение, частота вращения) вы можете обнаружить такой непонятный показатель, как косинус фи (cos ϕ). Данная информация может быть указана и на пластинке (шильдике), закрепленной на корпусе прибора. В нашей статье мы постараемся объяснить простым и доступным языком всем, даже пользователям далеким от электротехнических тонкостей, как тригонометрическая функция (знакомая нам со школьной скамьи) влияет на работу всем нам привычных электробытовых приборов, и почему ее называют коэффициентом мощности.
Важно! Все нижесказанное касается только сетей переменного тока. Далекий от электротехники, но весьма наглядный примерЧтобы объяснить, каким образом угол ϕ (а точнее его косинус) влияет на мощность, рассмотрим пример, не имеющий никакого отношения к электротехнике. Допустим нам необходимо передвинуть тележку, стоящую на рельсах. Чтобы удобнее было производить данную операцию, к ее передней части прикрепляем канат.
Если мы будем тянуть за веревку прямо вперед по направлению движения, то для перемещения тележки нам понадобится приложить достаточно небольшое усилие. Однако если находиться сбоку от рельсов и тянуть за канат в сторону, то для движения тележки с такой же скоростью необходимо будет приложить значительно большее усилие. Причем чем больше угол (ϕ) между направлением движения и прикладываемым усилием, тем больше «мощности» потребуется от нас.
Вывод! То есть, увеличение угла ϕ ведет к увеличению расходуемой нами энергии (при одной и той же выполненной работе). Сдвиг фаз между напряжением и токомПри использовании энергии переменного тока происходит приблизительно то же самое. При активной нагрузке (например, при включении электрочайника или лампы накаливания) переменные напряжение (U) и ток (I) полностью совпадают по фазе и одновременно достигают своих максимальных значений. В данном случае мощность потребителя электроэнергии можно рассчитать по формуле P=U•I.
Для сети переменного тока работающий электродвигатель, имеющийся, например, в стиральной машине, является комплексной нагрузкой, включающей в себя активную и индуктивную составляющие. При подаче напряжения на такой прибор оно появляется на обмотках, практически, мгновенно. А вот ток (из-за влияния индуктивности) запаздывает. То есть между ними образуется так называемый сдвиг фаз, который мы и называем ϕ.
При активно-емкостной нагрузке, наоборот, переменный ток сразу начинает течь через конденсатор, а напряжение отстает от него по фазе на величину ϕ.
Треугольник мощностейКоэффициент мощности (PF) – это отношение мощностей: активной полезной (P) к полной (S). Чтобы показать, каким образом сдвиг фаз влияет на PF, используем так называемый треугольник мощностей. И вот тут-то нам и потребуются минимальные знания школьной тригонометрии.
Из теории о прямоугольных треугольниках всем нам известно, что cos ϕ=P/S. То есть, косинус фи - это и есть коэффициент мощности (PF), который показывает, какая часть от полной мощности (S= U•I) фактически необходима для конкретной нагрузки. Чем больше реактивная составляющая Q, тем меньше полезная P. Чтобы вычислить активную мощность необходимо полную S умножить на косинус фи: P= S•cos ϕ. На заметку! Считать косинус фи абсолютным аналогом коэффициента мощности можно только при том условии, что мы имеем в электрической сети идеальную синусоиду. Для более точного расчета необходимо учитывать нелинейные искажения, которые имеют переменные напряжение и ток. На практике, зачастую коэффициентом нелинейных искажений синусоиды пренебрегают, и значение косинуса фи принимают за приближенное значение коэффициента мощности. Усредненные значения коэффициента мощностиЛампы накаливания и электрические нагревательные элементы, хотя и имеют в своих конструкциях спирали, намотанные с помощью специального провода, считаются чисто активной нагрузкой для сетей переменного тока. Так как индуктивность этих элементов настолько мала, что ею, как правило, просто пренебрегают. Для таких приборов cos ϕ (или коэффициент мощности) принимают равным 1. В разнообразных электрических ручных инструментах (дрелях, перфораторах, лобзиках и так далее) индуктивная составляющая мощности достаточно мала. Для них принято считать cos ϕ≈0,96÷0,97. Этот показатель достаточно близок к единице, поэтому его, практически, никогда не указывают в технических характеристиках. Для мощных электродвигателей, люминесцентных ламп и сварочных трансформаторов cos ϕ≈0,5÷0,82. Этот коэффициент мощности необходимо учитывать, например, при выборе диаметра питающих проводов, чтобы они не нагрелись, и не сгорела их изоляция.
На что влияет низкий коэффициент мощностиК чему могут привести низкие показатели коэффициента мощности:
В заключенииСмело можно утверждать, что чем ближе значение PF к единице, тем эффективнее используется электроэнергия. В некоторых мощных приборах производители устанавливают специальные приспособления, которые позволяют осуществлять коррекцию коэффициента мощности. artillum.ru 3.2 Выбор числа и мощности трансформаторов цтп с учетом компенсации реактивной мощности. Косинус фи трансформатораКосинус фи - простое объяснение в 3-х словах. Таблицы коэффициента мощности для различных потребителей.Многие из вас наверняка видели на электроинструментах, двигателях, а также люминесцентных лампах, лампах ДРЛ, ДНАТ и других, такие надписи как косинус фи — cos ϕ. Однако люди далекие от электротехники и позабывшие школьные уроки физики, не совсем понимают, что же означает данный параметр и зачем он вообще нужен. Давайте рассмотрим и объясним этот косинус, как можно более простыми словами, исключая всякие непонятные научные определения, типа электромагнитная индукция. В двух словах про него конечно не расскажешь, а вот в трех можно попробовать.Когда ток отстает от напряжения Предположим перед вами есть 2 проводника. Один из этих проводников имеет потенциал. Не суть важно какой именно — отрицательный (минус) или положительный (плюс). У другого провода вообще нет никакого потенциала. Соответственно между этими двумя проводниками будет разность потенциалов, т.к. у одного он есть, а у другого его нет. Эту разность потенциалов как раз таки и принято называть напряжением. Если вы соедините кончики двух проводов не непосредственно между собой, а через лампочку накаливания, то через ее вольфрамовую нить начнет протекать ток. От одного провода к другому. На первый взгляд может показаться, что лампочка загорается моментально. Однако это не так. Ток проходя через нить накала, будет нарастать от своего нулевого значения до номинального, какое-то определенное время.В какой-то момент он его достигает и держится на этом уровне постоянно. То же самое будет, если подключить не одну, а две, три лампочки и т.д. А что случится, если вместе с лампой последовательно включить катушку, намотанную из множества витков проволоки? Изменится ли как-то процесс нарастания тока? Конечно, да. Данная катушка индуктивности, заметно затормозит время увеличения тока от нуля до максимума. Фактически получится, что максимальное напряжение (разность потенциалов) на лампе уже есть, а вот ток поспевать за ним не будет. Его нарастание слишком медленное. Из-за чего это происходит и кто виноват? Виноваты витки катушки, которые оказывают влияние друг на друга и тормозят ток. Если у вас напряжение постоянное, например как в аккумуляторах или в батарейках, ток относительно медленно, но все-таки успеет дорасти до своего номинального значения. А далее, ток будет вместе с напряжением идти, что называется «нога в ногу». А вот если взять напряжение из розетки, с переменной синусоидой, то здесь оно не постоянно и будет меняться. Сначала U какое-то время положительная величина, а потом — отрицательная, причем одинаковое по амплитуде. На рисунке это изображается в виде волны. Эти постоянные колебания не дают нашему току, проходящему сквозь катушку, достигнуть своего установившегося значения и догнать таки напряжение. Только он будет подбираться к этой величине, а напряжение уже начинает падать. Поэтому в этом случае и говорят, что ток отстает от напряжения. Причем, чем больше в катушке намотано витков, тем большим будет это самое запаздывание. Как же это все связано с косинусом фи — cos ϕ? Что такое коэффициент мощности А связано это таким образом, что данное отставание тока измеряется углом поворота. Полный цикл синусоиды или волны, который она проходит от нуля до нуля, вместив в себя максимальное и минимальное значение, измеряется в градусах. И один такой цикл равен 360 градусов. А вот угол отставания тока от напряжения, как раз таки и обозначается греческой буквой фи. Значение косинуса этого угла опаздывания и есть тот самый cos ϕ. Таким образом, чем больше ток отстает от напряжения, тем большим будет этот угол. Соответственно косинус фи будет уменьшаться. По научному, ток сдвинутый от напряжения называется фазовым сдвигом. При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так. 10i5.ru 3.2 Выбор числа и мощности трансформаторов цтп с учетом компенсации реактивной мощности. Косинус фи трансформатораКосинус фи - простое объяснение в 3-х словах. Таблицы коэффициента мощности для различных потребителей.Многие из вас наверняка видели на электроинструментах, двигателях, а также люминесцентных лампах, лампах ДРЛ, ДНАТ и других, такие надписи как косинус фи — cos ϕ. Однако люди далекие от электротехники и позабывшие школьные уроки физики, не совсем понимают, что же означает данный параметр и зачем он вообще нужен. Давайте рассмотрим и объясним этот косинус, как можно более простыми словами, исключая всякие непонятные научные определения, типа электромагнитная индукция. В двух словах про него конечно не расскажешь, а вот в трех можно попробовать.Когда ток отстает от напряжения Предположим перед вами есть 2 проводника. Один из этих проводников имеет потенциал. Не суть важно какой именно — отрицательный (минус) или положительный (плюс). У другого провода вообще нет никакого потенциала. Соответственно между этими двумя проводниками будет разность потенциалов, т.к. у одного он есть, а у другого его нет. Эту разность потенциалов как раз таки и принято называть напряжением. Если вы соедините кончики двух проводов не непосредственно между собой, а через лампочку накаливания, то через ее вольфрамовую нить начнет протекать ток. От одного провода к другому. На первый взгляд может показаться, что лампочка загорается моментально. Однако это не так. Ток проходя через нить накала, будет нарастать от своего нулевого значения до номинального, какое-то определенное время.В какой-то момент он его достигает и держится на этом уровне постоянно. То же самое будет, если подключить не одну, а две, три лампочки и т.д. А что случится, если вместе с лампой последовательно включить катушку, намотанную из множества витков проволоки? Изменится ли как-то процесс нарастания тока? Конечно, да. Данная катушка индуктивности, заметно затормозит время увеличения тока от нуля до максимума. Фактически получится, что максимальное напряжение (разность потенциалов) на лампе уже есть, а вот ток поспевать за ним не будет. Его нарастание слишком медленное. Из-за чего это происходит и кто виноват? Виноваты витки катушки, которые оказывают влияние друг на друга и тормозят ток. Если у вас напряжение постоянное, например как в аккумуляторах или в батарейках, ток относительно медленно, но все-таки успеет дорасти до своего номинального значения. А далее, ток будет вместе с напряжением идти, что называется «нога в ногу». А вот если взять напряжение из розетки, с переменной синусоидой, то здесь оно не постоянно и будет меняться. Сначала U какое-то время положительная величина, а потом — отрицательная, причем одинаковое по амплитуде. На рисунке это изображается в виде волны. Эти постоянные колебания не дают нашему току, проходящему сквозь катушку, достигнуть своего установившегося значения и догнать таки напряжение. Только он будет подбираться к этой величине, а напряжение уже начинает падать. Поэтому в этом случае и говорят, что ток отстает от напряжения. Причем, чем больше в катушке намотано витков, тем большим будет это самое запаздывание. Как же это все связано с косинусом фи — cos ϕ? Что такое коэффициент мощности А связано это таким образом, что данное отставание тока измеряется углом поворота. Полный цикл синусоиды или волны, который она проходит от нуля до нуля, вместив в себя максимальное и минимальное значение, измеряется в градусах. И один такой цикл равен 360 градусов. А вот угол отставания тока от напряжения, как раз таки и обозначается греческой буквой фи. Значение косинуса этого угла опаздывания и есть тот самый cos ϕ. Таким образом, чем больше ток отстает от напряжения, тем большим будет этот угол. Соответственно косинус фи будет уменьшаться. По научному, ток сдвинутый от напряжения называется фазовым сдвигом. При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так. В качестве примера можно взять импульсные блоки питания. Не идеальность синусоиды выражается коэфф. нелинейных искажений — КНИ. Если сложить две эти величины — cos ϕ и КНИ, то вы получите коэффициент мощности. Однако, чтобы все не усложнять, чаще всего под понятием коэфф. мощности имеют в виду только лишь один косинус фи. На практике, данный коэффициент мощности рассчитывают не при помощи угла сдвига фаз, а отношением активной мощности к полной. Активная и 10i5.ru | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|
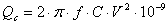[кВАр];
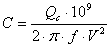[мФ], где
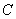- емкость конденсатора, [мкФ];
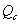- мощность конденсатора, [кВАр];
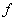- частота сети [Гц];
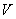- напряжение [В];
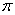- число ПИ (3,141592654).
