Комплексная мощность двухполюсника. Комплексная мощностьКомплексная мощность - Большая Энциклопедия Нефти и Газа, статья, страница 1Комплексная мощностьCтраница 1 Комплексная мощность является вектором с модулем, равным полной мощности UI, и с аргументом - ср. [1] Комплексная мощность равна произведению комплексного напряжения на сопряженный комплексный ток. [2] Комплексная мощность несимметричного режима может быть определена произведением матрицы-столбца комплексов токов на транспонированную матрицу-столбец сопряженных комплексов напряжений слева. [3] Комплексную мощность иногда определяют и как произведение сопряженного комплексного напряжения на комплексный ток. [4] Комплексной мощностью трехфазной системы называется сумма комплексных мощностей всех фаз источника энергии, равная сумме комплексных мощностей всех фаз приемника. [5] Модуль комплексной мощности равен полной мощности, а аргумент - углу сдвига фаз между напряжением и током. [6] Сумма комплексных мощностей всех ветвей цепи равна нулю. Равны нулю также сумма средних за период мощностей и сумма реактивных мощностей всех ветвей. [7] Модуль комплексной мощности равен полной мощности. [8] Поэтому комплексную мощность вычисляют, умножая комплексное напряжение на сопряженный комплексный ток. [9] Вычислим комплексную мощность источника. [10] Как связана полная комплексная мощность с активной и реактивной мощностями. [11] Как записывается полная комплексная мощность цепи через комплексы тока и напряжения. [12] Действительная часть комплексной мощности и является активной, измеряемой ваттметром. [13] Итак сумма комплексных мощностей, потребляемых всеми ветвями электрической цепи, равна нулю; следовательно, также равны нулю в отдельности алгебраические суммы действительных и мнимых частей мощностей. [14] Итак сумма комплексных мощностей, потребляемых всеми ветвями электрической цепи, равна нулю; следовательно, также равны нулю в отдельности алгебраические суммы действительных и мнимых частей мощностей. [15] Страницы: 1 2 3 www.ngpedia.ru 38. Комплексная мощность. Треугольник мощностей.Умножив стороны треугольника напряжение (рис. 4.17) на значение тока в цепи, получим треугольник мощностей (рис. 4.22). Здесь S - полная мощность, Q – реактивная мощность и Р - активная мощность. Из треугольника мощностей следует, что (4.48) Реактивная мощность Q всегда связана с обменом электрической энергией между источником и потребителем. Ее измеряют в вольт-амперах реактивных (вар). Полная мощность S содержит в себе как активную, так и реактивную составляющие - это мощность, которая потребляется от источника электроэнергии. При Р = 0 вся полная мощность становиться реактивной, а при Q=0- активной. Следовательно, составляющие полной мощности определяются характером нагрузки. Полная мощность измеряется в вольт амперах (ВА). Эта величина указывается на табличках приборов переменного тока. Активная мощность Р связана с той электрической энергией, которая может быть преобразована в другие виды энергии - теплоту, механическую работу и т.д. Она измеряется в ваттах (Вт). Активная мощность зависит от тока, напряжения и . При увеличении угла уменьшаются и мощность Р, а при уменьшении угла активная мощность Р возрастает. Таким образом, показывает, какая часть полной мощности теоретически может быть преобразована в другие виды энергии. Величина называется коэффициентом мощности. 39.Условие передачи максимума активной мощности от источника к приёмнику; то же для Zn Первое условие: Тогда получим :
Получили второе условие: Максимальная мощность, которая выделится на нагрузке:
40. Баланс мощностей в цепи переменного токаАлгебр. сумма комплексов мощностей, отдаваемых источниками, равна алгебр. сумме комплексов мощностей, потребляемых остальными элементами. Σ~S = Σ I* + Σ I(ист)* = Pист + jQист 41. Графоаналитический метод. Пример расчёта.Графоаналитический метод расчёта – это совок графического метода и метода пропорц пересчёта. Метод основан на линейной зависимости между токами и напряжениями. Поэтому векторная диаграмма напряжений и токов, рассчитанная и построенная для одного значения, питающего цепь напряжения, сохранит свой вид при изменении величины этого напряжения. На диаграмме изменятся лишь масштабы напряжений и токов Для ориентировочных расчетов напряжений и токов применяется также графоаналитический метод расчета. Этот метод методологически связан с методом пропорционального пересчета, однако не использует алгебры комплексных чисел. Пусть, как и в предыдущем методе, Выбрав масштабыидля напряжений и токов, откладывают в произвольном направлении ток(например горизонтально). Затем строят вектор напряжениясовпадающий по направлению с током,и вектор напряженияотстающий по фазе отна 90°. Используя графические измерения, вычисляют напряжениеВычисливи откладывая токпараллельнографически определяюти т.д. В результате находят вектор условного напряженияU. Затем с помощью коэффициента пересчета K=U/U' вычисляют истинные токи и напряжения. Графические построения по ходу расчета дают в итоге условную топографическую диаграмму. Для получения истинной диаграммы следует, во-первых, увеличить линейные размеры всех векторов в К раз, во-вторых, повернуть против часовой стрелки условную диаграмму на угол , равный разности начальных фаз векторови.Активная и реактивная мощности потребителей вычисляются по формулам
Комплексная мощность источника находится из
где – комплексное напряжение источника; I – сопряженный комплексный ток источника. studfiles.net Мощности в комплексной формеФормулы для определения полной, активной и реактивной мощностей записаны раньше
Рассмотрим простой прием, позволяющий найти активную и реактивную мощности по комплексным напряжению и току. Для этого умножим комплекс напряжения на сопряженный комплекс тока
Полученное значение
Пример 2.4. Определить активную, реактивную и полную мощности, если мгновенные значения тока и напряжения заданы уравнениями
Решение. Запишем комплексы действующих значений напряжений и тока
Комплекс полной мощности
Таким образом, 2.5. Повышение коэффициента мощности в цепях синусоидальноготока Большинство современных потребителей электрической энергии имеют индуктивный характер нагрузки, токи которой отстают по фазе от напряжения источника. Активная мощность таких потребителей при заданных значениях тока и напряжения зависит от
Следовательно, повышение коэффициента мощности приводит к уменьшению тока. Если обозначить сопротивление проводов линии
Таким образом, чем выше
а при Следовательно, повышение
Рис. 2.18 Емкость конденсатора, необходимую для повышения После подключения к потребителю батареи конденсаторов ток Емкость конденсатора можно рассчитать при помощи векторной диаграммы токов (рис. 2.18 в)
Учитывая, что
На практике обычно коэффициент мощности повышают не до 1,0, а до 0,90...0,95, так как полная компенсация требует дополнительной установки конденсаторов, что часто экономически не оправдано.
Общие сведения
При рассмотрении цепей синусоидального тока до сих пор учитывалось только явление самоиндукции катушек, обусловленное током в цепи. Цепи, в которых наводятся ЭДС между двумя (и более) взаимно связанными катушками, называются индуктивно связанными цепями.Рассмотрим явление возникновения ЭДС в одном из контуров при изменении тока в другом. Контуры (рис. 2.19) представляют собой плоские тонкие катушки с числами витков
Аналогично определяем поток самоиндукции второго контура
Потоки
где «+» соответствует согласному направлению потоков, «–» – встречному направлению. Полные потокосцепления первого и второго контуров
Отношение потокосцепления взаимной индукции в одной цепи к току в другой называется взаимной индуктивностью
Для линейных электрических цепей всегда выполняется равенство
Взаимная индуктивность двух катушек зависит от числа витков, геометрических размеров магнитопровода и взаимного расположения катушек, а также от абсолютной магнитной проницаемости среды (материала магнитопровода). Индуктивную связь двух катушек характеризуют коэффициентом связи
Этот коэффициент всегда меньше единицы, так как магнитный поток взаимной индукции всегда меньше потока самоиндукции и может быть увеличен за счет уменьшения потоков рассеяния бифилярной намоткой катушек (двойным проводом) или применением для магнитопровода материала с высокой абсолютной магнитной проницаемостью.
Похожие статьи:poznayka.org Полная мощностьПомимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:
Активная, реактивная и полная мощности связаны следующим соотношением:
Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощностиравен косинусу угла сдвига между током и напряжением. Итак,
Комплексная мощностьАктивную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а. Тогда комплекс полной мощности:
где - комплекс, сопряженный с комплексом. . 33.
Представление синусоидальных величин с помощью векторов и комплексных чиселПеременный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения. В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ. Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц. Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой: i - мгновенное значение тока ; u – мгновенное значение напряжения ; е - мгновенное значение ЭДС ; р- мгновенное значение мощности . Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m). - амплитуда тока; - амплитуда напряжения; - амплитуда ЭДС. studfiles.net Режим гармонических колебаний. Частотные характеристикиКомплексное число , модуль которого равен полной мощности цепи S, а аргумент – углу сдвига фаз между током и напряжением , называется комплексной мощностью цепи: (2.52) Переходя от показательной формы записи Sк тригонометрической, получаем (2.53) Вещественная часть комплексной мощности равна активной мощности цепи: (2.54) Мнимая часть комплексной мощности представляет собой реактивную мощность цепи: (2.55) Реактивная мощность характеризует процессы обмена энергией между цепью и источником, она численно равна максимальной скорости запасения энергии в цепи. С учетом (2.54) и (2.55) выражение (2.53) можно записать следующим образом: (2.56) Следовательно, комплексная мощность представляет собой комплексное число, вещественная часть которого равна активной мощности цепи P, а мнимая – реактивной Q. Комплексному числу можно поставить в соответствие вектор , проекции которого на вещественную и мнимую оси равны P и Q. Прямоугольный треугольник с гипотенузой, равной S, и катетами Pи Q называется треугольником мощностей. В связи с тем, что треугольник мощностей цепи подобен треугольнику сопротивлений этой же цепи, комплексная мощность и ее компоненты S, P, Q могут быть выражены через комплексное сопротивление цепи Z и его компоненты z, r, x: (2.57) Можно найти связь между комплексной мощностью и комплексными действующими значениями тока и напряжения на зажимах цепи. Подставляя в (2.52) выражения и , получаем (2.58) где - число, комплексно–сопряженное с током (комплексно–сопряженный ток). Таким образом, комплексная мощность цепи равна произведению комплексного напряжения цепи на комплексно–сопряженный ток . Пример 2.4. Рассчитать полную, активную, реактивную и комплексную мощности произвольного двухполюсника, если напряжение и ток на зажимах двухполюсника изменяются по гармоническому закону:
Определим комплексный ток , комплексное напряжение и сдвиг фаз между током и напряжением на зажимах двухполюсника:
Подставляя эти величины в , , (2.55), и (2.52), находим искомые мощности:
3ys.ru Комплексная мощностьДопустим, имеется пассивный двухполюсник, изображенный на рисунке 3.66, на зажимы которого приложено синусоидальное напряжение
Запишем комплекс действующего значения напряжения Комплексом полной мощности
где -
Запишем комплекс полной мощности в алгебраической форме:
Из вышеуказанного следует, что действительная часть комплексной мощности представляет собой активную мощность, а мнимая мощность – реактивную. В разветвленных электрических цепях, в которых имеются несколько источников напряжения и токов, полная мощность источников равна Баланс мощностей разветвленной электрической цепи с несколькими источниками питания имеет вид:
Похожие статьи:poznayka.org комплексная мощность — с русскогоСм. также в других словарях:
translate.academic.ru |
|
||||||||||||||||||
|
|
||||||||||||||||||
|




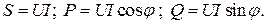
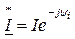
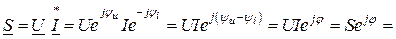
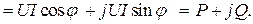 (2.46)
(2.46)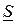 называют комплексом полной мощности. Из (2.46) видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной:
называют комплексом полной мощности. Из (2.46) видно, что вещественная часть комплексной мощности равна активной мощности, мнимая часть – реактивной: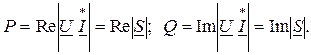 (2.47)
(2.47)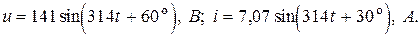
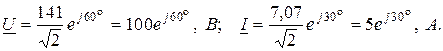
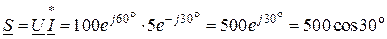 +
+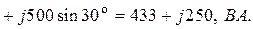
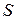 = 500 ВА,
= 500 ВА, 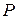 = 433 Вт,
= 433 Вт, 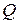 = 250 вар.
= 250 вар.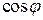
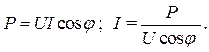
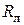 , то потери мощности в ней можно определить так:
, то потери мощности в ней можно определить так: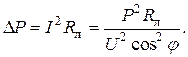
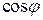 потребителя, тем меньше потери мощности в линии и дешевле передача электроэнергии. Коэффициент мощности показывает, как используется номинальная мощность источника. Так, для питания приемника 1000 кВт при
потребителя, тем меньше потери мощности в линии и дешевле передача электроэнергии. Коэффициент мощности показывает, как используется номинальная мощность источника. Так, для питания приемника 1000 кВт при 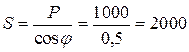 кВА,
кВА,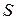 = 1000 кВА.
= 1000 кВА.
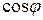 от существующего значения
от существующего значения 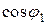 до требуемого
до требуемого 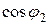 , можно определить по диаграмме (рис. 2.18 б, в). При построении векторной диаграммы в качестве исходного вектора принят вектор напряжения источника. Если нагрузка представляет собой индуктивный характер, то вектор тока
, можно определить по диаграмме (рис. 2.18 б, в). При построении векторной диаграммы в качестве исходного вектора принят вектор напряжения источника. Если нагрузка представляет собой индуктивный характер, то вектор тока 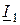 отстает от вектора напряжения на угол
отстает от вектора напряжения на угол 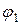 . Активная составляющая тока
. Активная составляющая тока 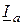 совпадает по направлению с напряжением, реактивная составляющая тока
совпадает по направлению с напряжением, реактивная составляющая тока 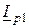 отстает от него на 90° (рис. 2.18 б).
отстает от него на 90° (рис. 2.18 б).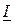 определяется как геометрическая сумма векторов
определяется как геометрическая сумма векторов 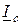 . При этом вектор емкостного тока
. При этом вектор емкостного тока 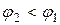 , т.е. после включения конденсатора коэффициент мощности повышается от
, т.е. после включения конденсатора коэффициент мощности повышается от 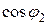 .
.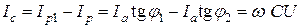 .
.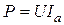 , запишем емкость конденсатора
, запишем емкость конденсатора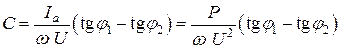 .
. 2.6. Электрические цепи с взаимной индуктивностью
2.6. Электрические цепи с взаимной индуктивностью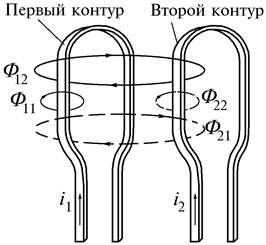 Рис. 2.19
Рис. 2.19
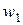 и
и 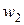 . Поток самоиндукции
. Поток самоиндукции 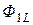 , созданный током
, созданный током 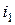 , может быть представлен в виде потока рассеяния
, может быть представлен в виде потока рассеяния 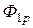 , пронизывающего только первый контур, и потока
, пронизывающего только первый контур, и потока 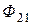 , пронизывающего второй контур
, пронизывающего второй контур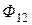 .
.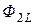 =
= 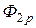 +
+ 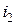 , сцепляется с первым контуром. Если направление потока взаимной индукции совпадает с направлением потока самоиндукции данного контура, то говорят, что магнитные потоки и токи контуров направлены согласно. В случае противоположного направления говорят о встречном направлении потоков. Суммарные потоки, пронизывающие первый и второй контуры
, сцепляется с первым контуром. Если направление потока взаимной индукции совпадает с направлением потока самоиндукции данного контура, то говорят, что магнитные потоки и токи контуров направлены согласно. В случае противоположного направления говорят о встречном направлении потоков. Суммарные потоки, пронизывающие первый и второй контуры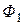 =
= 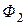 =
= 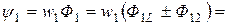
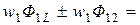
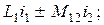 (2.48)
(2.48)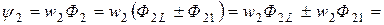
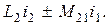 (2.49)
(2.49)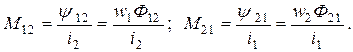
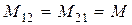 .
.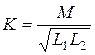 .
.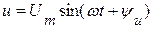 и протекает синусоидальный ток
и протекает синусоидальный ток 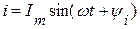 .
.
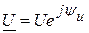 и тока
и тока 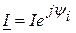 .
.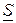 называется произведение комплекса напряжения
называется произведение комплекса напряжения 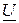 на сопряженный комплекс тока
на сопряженный комплекс тока 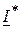 :
: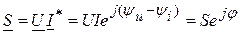 ,
,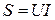 - полная мощность, потребляемая двухполюсником,
- полная мощность, потребляемая двухполюсником,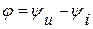 - сдвиг по фазе между током и напряжением.
- сдвиг по фазе между током и напряжением.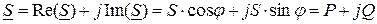 .
.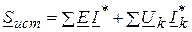 , где
, где 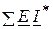 - суммарная комплексная мощность источников напряжения, а
- суммарная комплексная мощность источников напряжения, а 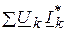 - суммарная комплексная мощность источников тока.
- суммарная комплексная мощность источников тока.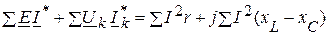 .
.





