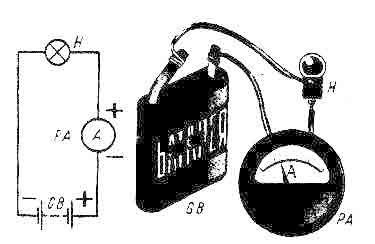
Основы электротехники. Как в электротехнике найти i

Основы электротехники

Некоторые люди утверждают, что изучение электрических законов и формул - это пустая трата времени для установщика. В конце концов, мастер определяет сечение силового кабеля, место заземления или устраняет шум в аудиосистеме безо всяких формул и математики. Практический опыт - незаменимая вещь! Тем не менее, понимание того, что данный калибр провода мал или что является причиной шума в установленной звуковой системе, поможет Вам во многих практических ситуациях. Знание основ электротехники поможет Вам логически найти причину неисправности и быстро устранить ее.

Прежде чем перейти к математическим соотношениям, присутствующим в электротехнике, необходимо вкратце рассказать о двух типах тока, с которыми Вам придется работать в автомобиле с аудиосистемами. Это постоянный и переменный ток.

Переменный ток - это электрический ток, у которого периодически меняется полярность (то есть, переходит от положительной к отрицательной). В цепи переменного тока поток электронов меняет направление в каждый полупериод. Скорость периодического изменения называется частотой, которая измеряется в Герцах.

Переменный ток (AC) - питает канал звукового сигнала, начинает свой путь в головном устройстве (автомагнитоле), далее через процессор для обработки сигналов поступает в усилитель, где усиливается до необходимого уровня и, наконец, попадает на звуковую катушку динамика, которая приводит в движение его мембрану.

Постоянный ток (DC) - это ток, которым питаются все вышеперечисленные компоненты аудиосистемы и все электрические устройства автомобиля.

Электрический ток. При движении заряженных частиц в проводнике происходит перенос электрического заряда с одного места в другое. Однако если заряженные частицы совершают беспорядочное тепловое движение, как, например, свободные электроны в металле, то переноса заряда не происходит. Электрический заряд перемещается через поперечное сечение проводника лишь в том случае, если наряду с беспорядочным движением электроны участвуют в упорядоченном движении. В этом случае говорят, что в проводнике устанавливается электрический ток. Электрическим током называют упорядоченное движение заряженных частиц (электронов или ионов).

Электрический ток имеет определенное направление. О наличии электрического тока приходится судить по тем действиям или явлениям, которые его сопровождают.

Во-первых, проводник, по которому течет ток, нагревается.

Во-вторых, электрический ток может изменять химический состав проводника.

В-третьих, ток оказывает силовое воздействие на соседние токи, проводники и намагниченные тела.

Если в цепи устанавливается электрический ток, то это означает, что через поперечное сечение проводника все время переносится электрический заряд. Заряд, перенесенный в единицу времени, называется силой тока. Если сила тока со временем не меняется, то ток называют постоянным. Сила тока выражается в Амперах.

Для создания и поддержания движения заряженных частиц, необходима сила, действующая на них в определенном направлении. Если эта сила перестанет действовать, то ток прекратится. Эту силу принято называть электрическим полем или напряженностью электрического поля, которое порождает разность потенциалов на концах проводника и обеспечивает движение частиц. Когда разность потенциалов (напряжение) не меняется во времени, то в проводнике устанавливается постоянный электрический ток. Чем больше напряжение, тем выше сила тока. Зависимость между силой тока и напряжением выражает закон Ома:

I = U/R

Сила тока I прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению проводника R.

Сопротивление - это основная электрическая характеристика проводника. От сопротивления зависит сила тока при заданном напряжении. Сопротивление измеряется в Омах. Проводник имеет сопротивление 1 Ом, если при разности потенциалов 1 В сила тока в нем равна 1 А. Сопротивление проводника представляет собой меру противодействия проводника установлению в нем электрического тока. Результат сопротивления проводника, - это его нагрев. Сопротивление проводника зависит от его длины и сечения. Чем больше длина и меньше сечение проводника, тем больше его сопротивление.

Закон Ома. Этот закон является одним из самых основных законов электротехники. Закон Ома описывает соотношение между силой тока, напряжением, сопротивлением и мощностью. Давайте поближе рассмотрим эти параметры и то, как они используются в автомобильной электротехнике.

Напряжение представляет из себя электрическое давление, которое передвигает заряженные частицы в контуре.

Ток - это скорость (интенсивность) потока электронов через сечение проводника. Электрическое сопротивление определяет электрическую проводимость, которой обладает проводник. Низкая проводимость оказывает сопротивление потоку электричества. Сопротивление провода определяется удельной электрической проводимостью материала, его сечением и длиной.

Следующие формулы вытекают из закна Ома:

I = U/R сила тока (Ампер)

U = IxR напряжение (Вольт)

R = U/I сопротивление (Ом)

В соответствии с законом Ома, если Вы хотите найти силу тока (I), Вам следует разделить напряжение (U) на сопротивление (R). Для нахождения напряжения умножаем силу тока на сопротивление. И для того, чтобы найти сопротивление необходимо разделить напряжение на силу тока.

Давайте подойдем к пониманию зависимости между силой тока, напряжением и сопротивлением через сравнение электрических характеристик с гидравликой.

Представьте, что у Вас имеется бак с водой. У основания бака установлен клапан, к которому примыкает труба. Другой конец трубы открыт. Если клапан открыть, то по трубе потечет вода в силу разности давления между началом трубы (высокое давление) и ее концом (низкое давление). Это аналогично разности потенциалов на концах проводника (напряжение), которое заставляет двигаться электроны по проводнику. То есть напряжение можно условно считать электрическим "давлением". Сила тока аналогична расходу воды, то есть количеству воды, протекающей через сечение трубы за определенный промежуток времени. Если уменьшить диаметр трубы, то поток воды уменьшится, поскольку увеличивается сопротивление. Это ограничение величины потока сравнимо с электрическим сопротивлением, которое держит в определенных пределах поток электронов. Соотношение между током, напряжением и сопротивлением схоже с водяным баком - меняется один параметр, и меняются все остальные.

Закон Ома поможет Вам избежать множество проблем, возникающих при установке автомобильных аудиосистем.

К примеру, Вы подаете питание на аудиосистему высокой мощности (Ватт), но сечение выбранного Вами провода оказывается слишком мало для подачи тока, необходимого системе. Сопротивление провода будет давать падение напряжения по всей его длине, когда усилители будут забирать энергию. Усилители, работающие при пониженном напряжении, могут перегреваться, генерировать низкие частоты (гул) или выходить из строя. В свою очередь, из-за большого сопротивления провод начнет перегреваться, что может привести к его возгоранию. Используя закон Ома можно рассчитать силу тока в проводнике, зная напряжение и потребляемую мощность. И далее, для найденной силы тока подбирается нужное сечение провода.

Закон Ома целесообразно применять, когда необходимо просчитать действующее сопротивление устройства (например, усилителя) в работающем контуре. Замерять сопротивление напрямую в цепи под напряжением нельзя, но его можно определить математически, пользуясь законом Ома.

Допустим, усилитель потребляет ток в 50 ампер при напряжении 12 вольт. Действующее (эффективное) сопротивление услителя будет равно:

R = U/I

R = 12В/50А

Rэф = 0.24Ом

Электрическая энергия. Закон Ома имеет отношение к четвертому параметру контура - мощности. Существуют различные формы энергии: механическая, тепловая, ядерная и электрическая. Закон сохранения энергии утверждает, что нельзя создать или уничтожить энергию, она может только быть преобразована в другую форму энергии. Этот же закон действует в аудиоконтурах, где электрическая энергия преобразуется в теплоту и звук. Любой электрический прибор (лампа, электродвигатель) рассчитан на потребление определенной энергии в единицу времени. Электрическая мощность равна отношению работы тока к интервалу времени, за который произведена работа. Используя закон Ома, мощность тока представляется следующим образом:

P = IxU

Электрическая мощность измеряется в Ваттах. Один вольт переместит один ампер через один ом сопротивления с интенсивностью работы в один ватт. Из формулы мощности можно вывести формулу определения силы тока при заданном напряжении:

I = P/U

Это очень важная формула, которая помогает установщику правильно определить потребление тока аудиосистемой при известной выходной мощности (RMS) усилителя и напряжения в сети автомобиля. Зная потребляемую силу тока установщик из специальной таблицы подбирает нужное сечение (калибр) силового кабеля для звуковой системы.

Об этом подробно рассказывается в статье <u>"Методика установки автомобильных аудиосистем"</u>.

Полезные темы:

magnitola.org

Урок-4. ОСНОВЫ ЭЛЕКТРОТЕХНИКИ

ОСНОВЫ ЭЛЕКТРОТЕХНИКИ

Все что будет дано в этом уроке, необходимо не только прочитать и запомнить некоторые ключевые моменты, а и зазубрить некоторые определения и формулировки. Именно с этого урока начнутся элементарные физические и электрические расчеты. Возможно, будет не все понятно, но не надо отчаиваться, все со временем станет на свои места, главное не спеша усваивать и запоминать материал. Даже если по началу не все будет понятно, постарайтесь хотя бы запомнить основные правила и те элементарные формулы, которые здесь будут рассматриваться. Хорошенько освоив этот урок, вы потом сможете выполнять более сложные радиотехнические расчеты и решать необходимые задачи. Без этого в радиоэлектронике не обойтись. Дабы подчеркнуть значимость данного урока, все формулировки и определения, которые необходимо заучить я буду выделять красным курсивом.

ЭЛЕКТРИЧЕСКИЙ ТОК И ЕГО ОЦЕНКА

До сих пор, характеризуя количественное значение электрического тока, я иногда пользовался такой терминологией, как, например, малый ток, большой ток. На первых порах такая оценка тока как - то нас устраивала, но она совершенно непригодна для характеристики тока с точки зрения работы которую он может выполнять. Когда мы говорим о работе тока, под - этим подразумеваем, что его энергия преобразуется в какой-либо иной вид энергии: тепло, свет, химическую или механическую энергию. Чем больше поток электронов, тем значительнее ток и его работа. Иногда говорят, сила тока или просто ток. Таким образом слово ток имеет два значения. Оно обозначает само явление движения электрических зарядов в проводнике, а так же служит оценкой количества электричества, проходящего по проводнику. Ток (или силу тока) оценивают количеством электронов, проходящих по проводнику в течение 1 с. Число его огромно. Через нить накала горящей лампочки электрического карманного фонарика, например, ежесекундно проходит около 2000000000000000000 электронов. Вполне понятно, что характеризовать ток количеством электронов неудобно, так как пришлось бы иметь дело с очень большими числами. За единицу электрического тока принят Ампер (сокращенно пишут А). Так ее назвали в честь французского физика и математика А. Ампера (1775 - 1836 гг.), изучившего законы механического взаимодействия проводников с током и другие электрические явления. Ток 1 А - это ток такого значения, при котором через поперечное сечение проводника за 1 с проходит 6250000000000000000 электронов. В математических выражениях ток обозначают латинской буквой I или i (читается и). Например, пишут: I 2 А или 0,5 А. Наряду с ампером применяют более мелкие единицы силы тока: миллиампер (пишут мА), равный 0,001 А, и микроампер (пишут мкА), равный 0,000001 А, или 0,001 мА. Следовательно, 1 А = 1000 мА или 1000000 мкА. Приборы, служащие для измерения токов, называют соответственно амперметрами, миллиамперметрами, микроамперметрами. Их включают в элетрическую цепь последовательно с потребителем тока, т.е. в разрыв внешней цепи. На схемах эти приборы изображают кружками с присвоенным им буквами внутри: А (амперметр), (миллиамперметр) и мА (микроампер) мкА., а рядом пишут РА, что означает измеритель тока. Измерительный прибор рассчитан на ток не больше некоторого предельного для данного прибора. Прибор нельзя включать в цепь, в которой течет ток, превышающий это значение, иначе он может испортиться.

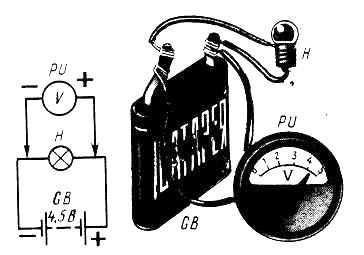
Амперметр (миллиамперметр, кроамперметр) включают в электрическую цепь последовательно с потребителем тока.

У вас может возникнуть вопрос: как оценить переменный ток, направление и величина которого непрерывно изменяются? Переменный ток обычно оценивают по его действующему значению. Это такое значение тока, которое соответствует постоянному току, производящему такую же работу. Действующее значение переменного тока составляет примерно 0,7 амплитудного, т. е. максимального значения.

ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ

Говоря о проводниках, мы имеем в виду вещества, материалы и прежде всего металлы, относительно хорошо проводящие ток. Однако не все вещества, называемые проводниками, одинаково хорошо проводят электрический ток, т. е. они, как говорят, обладают неодинаковой проводимостью тока. Объясняется это тем, что при своем движении свободные электроны сталкиваются с атомами и молекулами вещества, причем в одних веществах атомы и молекулы сильнее мешают движению электронов, а в других - меньше. Говоря иными словами, одни вещества оказывают электрическому току большее сопротивление, а другие - меньшее. Из всех материалов, широко применяемых в электротехнике и радиотехнике, наименьшее сопротивление электрическому току оказывает медь. Поэтому - то электрические провода и делают чаще всего из меди. Еще меньшее сопротивление имеет серебро, но это довольно дорогой металл. Железо, алюминий и разные металлические сплавы обладают большим сопротивлением, т. е. худшей электропроводимостью. Сопротивление проводника зависит не только от свойств его материала, но и от размера самого проводника. Толстый проводник обладает меньшим сопротивлением, чем тонкий из такого же материала; короткий проводник имеет меньшее сопротивление, длинный - большее, так же как широкая и короткая труба оказывает меньшее препятствие движению воды, чем тонкая и длинная. Кроме того, сопротивление металлического проводника зависит от его температуры: чем ниже температура проводника, тем меньше его сопротивление. За единицу электрического сопротивления принят ом (пишут Ом) - по имени немецкого физика Г. Ома. Сопротивление 1 Ом - сравнительно небольшая электрическая величина. Такое сопротивление току оказывает, например, отрезок медного провода диаметром 0,15 мм и длиной 1 м. Сопротивление нити накала лампочки карманного электрического фонаря около 10 Ом, нагревательного элемента электроплитки - несколько десятков ом. В радиотехнике чаще приходится иметь дело с большими, чем ом или несколько десятков ом, сопротивлениями. Сопротивление высокоомного телефона, например, больше 2000 Ом; сопротивление полупроводникового диода, включенного в не пропускающем ток направлении, несколько сотен тысяч ом. Знаете, какое сопротивление электрическому току оказывает ваше тело? От 1000 до 20000 Ом. А сопротивленце резисторов - специальных деталей, о которых я буду еще говорить в этой беседе, могут быть до нескольких миллионов ом и больше. Эти детали, как вы уже знаете, на схемах обозначают в виде прямоугольников. В математических формулах сопротивление обозначают латинской буквой (R). Такую же букву ставят и возле графических обозначений резисторов на схемах. Для выражения больших сопротивлений резисторов используют более крупные единицы: килоом (сокращенно пишут кОм), равный 1000 Ом, и мегаом (сокращенно пишут МОм), равный 1000000 Ом, или 1000 кОм. Сопротивления проводников, электрических цепей, резисторов или других деталей измеряют специальными приборами, именуемыми омметрами. На схемах омметр обозначают кружком с греческой буквой ? (омега) внутри.

ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНИЕ

За единицу электрического напряжения, электродвижущей силы (ЭДС) принят вольт (в честь итальянского физика А. Вольта). В формулах напряжение обозначают латинской буквой U (читается «у»), а саму единицу напряжения - вольт - буквой В. Например, пишут: U = 4,5 В; U = 220 В. Единица вольт характеризует напряжение на концах проводника, участке электрической цепи или полюсах источника тока. Напряжение 1 В - это такая электрическая величина, которая в проводнике сопротивлением 1 Ом создает ток, равный 1 А. Батарея 3336Л, предназначенная для плоского карманного электрического фонаря, как вы уже знаете, состоит из трех элементов, соединенных последовательно. На этикетке батареи можно прочитать, что ее напряжение 4,5 В. Значит, напряжение каждого из элементов батареи 1,5 В. Напряжение батареи «Крона» 9 В, а напряжение электроосветительной сети может быть 127 или 220 В. Напряжение измеряют (вольтметром), подключая прибор одноименными зажимами к полюсам источника тока или параллельно участку цепи, резистору или другой нагрузке, на которой необходимо измерить действующее на ней напряжение На схемах вольтметр обозначают латинской буквой V.

Вольтметр подключают параллельно нагрузке или источнику тока, питающего электрическую цепь.

в кружке, а рядом - PU. Для оценки напряжения применяют и более крупную единицу - киловольт (пишут кВ), соответствующую 1000 В, а также более мелкие единицы - милливольт (пишут мВ), равный 0,001 В, и микровольт (пишут мкВ), равный 0,001 мВ. Эти напряжения измеряют соответственно кило - вольтметрами, милливольтметрами и микровольтметрами. Такие приборы, как и вольтметры, подключают параллельно источникам тока или участкам цепей, на которых надо измерить напряжение. Выясним теперь, в чем разница понятий «напряжение» и «электродвижущая сила». Электродвижущей силой называют напряжение, действующее между полюсами источника тока, пока к нему не подключена внешняя цепь-нагрузка, например лампочка накаливания или резистор. Как только будет подключена внешняя цепь и в ней возникнет ток, напряжение между полюсами источника тока станет меньше. Так, например, новый не бывший еще в употреблении гальванический элемент имеет ЭДС не менее 1,5 В. При подключении к нему нагрузки напряжение на его полюсах становится равным примерно 1,3-1,4 в. По мере расходования энергии элемента на питание внешней цепи его напряжение постепенно уменьшается. Элемент считается разрядившимся и, следовательно, негодным для дальнейшего применения, когда напряжение снижается до 0,7 В, хотя, если отключить внешнюю цепь, его ЭДС будет больше этого напряжения. А как оценивают переменное напряжение? Когда говорят о переменном напряжении, например о напряжении электроосветительной сети, то имеют в виду его действующее значение, составляющее примерно, как и действующее значение переменного тока, 0,7 амплитудного значения напряжения.

ЗАКОН ОМА

На рис. показана схема знакомой вам простейшей электрической цепи. Эта замкнутая цепь состоит из трех элементов: источника напряжения - батареи GB, потребителя тока - нагрузки R, которой может быть, например, нить накала электрической лампы или резистор, и проводников, соединяющих источник напряжения с нагрузкой. Между прочим, если эту цепь дополнить выключателем, то получится полная схема карманного электрического фонаря.

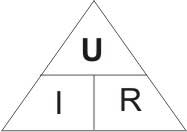
Простейшая электрическая цепь постоянного тока.

Нагрузка R, обладающая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи зависит от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем большим ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается следующей формулой: I = U/R,где I - ток, выраженный в амперах, А; U - напряжение в вольтах, В; R - сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и обратно пропорционален его сопротивлению. Это основной закон электротехники, именуемый законом Ома (по фамилии Г. Ома), для участка электрической цепи. Используя закон Ома, можно по двум известным электрическим величинам узнать неизвестную третью. Вот несколько примеров практического применения закона Ома.

Первый пример: На участке цепи, обладающем сопротивлением 5 Ом, действует напряжение 25 В. Надо узнать значение тока на этом участке цепи.Решение: I = U/R = 25 / 5 = 5 А.Второй пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Прежде всего ток 20 мА нужно выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом.

Третий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Здесь, как и в предыдущем примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Следовательно, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем говорят эти сведения? О том, что лампочка будет нормально светиться при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, нетрудно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити значительно меньше. Закон Ома справедлив не только для участка, но и для всей электрической цепи. В этом случае в значение R подставляется суммарное сопротивление всех элементов цепи, в том числе и внутреннее сопротивление источника тока. Однако при простейших расчетах цепей обычно пренебрегают сопротивлением соединительных проводников и внутренним сопротивлением источника тока.

В связи с этим приведу еще один пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Примерно такой ток потребляет электрический паяльник.

Всеми этими формулами, вытекающими из закона Ома, можно пользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов.

Закон Ома и производные от него расчетные формулы, достаточно легко запомнить, если пользоваться вот этой графической схемой, т. н. треугольник закона Ома:

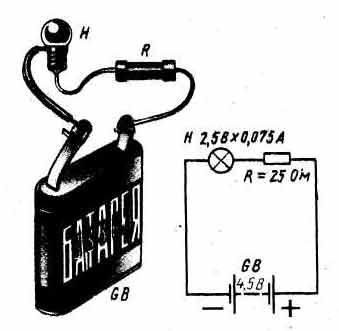
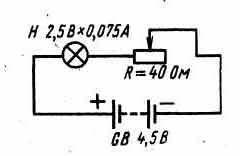
Пользоваться этим треугольником легко, достаточно четко запомнить, что горизонтальная линия в треугольнике означает знак деления (по аналогии дробной черты), а вертикальная линия в треугольнике означает знак умножения.

Теперь рассмотрим такой вопрос: как влияет на ток резистор, включаемый в цепь последовательно с нагрузкой или параллельно ей? Разберем такой пример. У нас имеется лампочка от круглого электрического, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, начальное напряжение которой 4,5 В? Нетрудно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, почти вдвое превышающий тот ток, на который она рассчитана. Такой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все же можно питать от батареи 336Л, если последовательно в цепь включить добавочный резистор сопротивлением 25 Ом, как это показано на рис..

Добавочный резистор, включенный в цепь, ограничивает ток в этой цепи.

В этом случае общее сопротивление внешней цепи будет равно примерно 55 Ом, т.е. 30 Ом - сопротивление нити лампочки Н плюс 25 Ом - сопротивление добавочного резистора R. В цепи, следовательно, потечет ток, равный примерно 0,08 А, т.е. почти такой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высоким напряжением и даже от электроосветительной сети, если подобрать резистор соответствующего сопротивления. В этом примере добавочный резистор ограничивает ток в цепи до нужного нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В данном случае в цепь было включено последовательно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при последовательном соединении сопротивлений ток одинаков во всех точках цепи. Можно включать амперметр в любую точку цепи, и всюду он будет показывать одно значение. Это явление можно сравнить с потоком воды в реке. Русло реки на различных участках может быть широким или узким, глубоким или мелким. Однако за определенный промежуток времени через поперечное сечение любого участка русла реки всегда проходит одинаковое количество воды.

Добавочный резистор, включаемый в цепь последовательно с нагрузкой (как, например, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится добавочным резистором или, как говорят, падает на нем, будет тем большим, чем больше сопротивление этого резистора. Зная ток и сопротивление добавочного резистора, падение напряжения на нем легко подсчитать все по той же знакомой вам формуле U = IR, Здесь U - падение напряжения, В; I - ток в цепи, A; R - сопротивление добавочного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил избыток напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное приблизительно 2,5 В, упало на нити лампочки. Необходимое сопротивление резистора можно найти по другой знакомой вам формуле R = U/I, где R - искомое сопротивление добавочного резистора, Ом; U-напряжение, которое необходимо погасить, В; I - ток в цепи, А. Для нашего примера сопротивление добавочного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать или увеличивать напряжение, которое падает на добавочном резисторе, и таким образом регулировать ток в цепи. Но добавочный резистор R в такой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже).

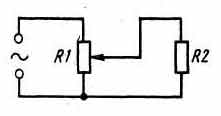
Регулирование тока в цепи с помощью переменного резистора.

В этом случае с помощью движка резистора можно плавно изменять напряжение, подводимое к нагрузке Н, а значит, плавно регулировать ток, протекающий через эту нагрузку. Включенный таким образом переменный резистор называют реостатом, С помощью реостатов регулируют токи в цепях приемников, телевизоров и усилителей. Во многих кинотеатрах реостаты использовали для плавного гашения света в зрительном зале. Есть, однако, и другой способ подключения нагрузки к источнику тока с избыточным напряжением - тоже с помощью переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис..

Регулирование напряжения на нагрузке R2 с помощью переменного резистора включенного в электрическую цепь потенциометром.

Здесь R1 - резистор, включенный потенциометром, a R2 - нагрузка, которой может быть та же лампочка накаливания или какой - то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое частично или полностью может быть подано к нагрузке R2. Когда движок резистора находится в крайнем нижнем положении, к нагрузке напряжение вообще не подается (если это лампочка, она гореть не будет). По мере перемещения движка резистора вверх мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в крайнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 - лампочка карманного фонаря, а напряжение источника тока большое, нить лампочки перегорит). Можно опытным путем найти такое положение движка переменного резистора, при котором к нагрузке будет подано необходимое ей напряжение. Переменные резисторы, включаемые потенциометрами, широко используют для регулирования громкости в приемниках и усилителях. Резистор может быть непосредственно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет двумя параллельными путями: через добавочный резистор и основную нагрузку. Наибольший ток будет в ветви с наименьшим сопротивлением. Сумма же токов обеих ветвей будет равна току, расходуемому на питание внешней цепи. К параллельному соединению прибегают в тех Случаях, когда надо ограничить ток не во всей цепи, как при последовательном включении добавочного резистора, а только на каком - то участке. Добавочные резисторы подключают, например, параллельно миллиамперметрам, чтобы ими можно было измерять большие токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление.

ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ

В цепи переменного тока на значение тока влияет не только сопротивление проводника, включенного в цепь, но и его индуктивность. Поэтому в цепях переменного тока различают так называемое омическое или активное сопротивление, определяемое свойствами материала проводника, и индуктивное сопротивление, определяемое индуктивностью проводника. Прямой проводник обладает сравнительно небольшой индуктивностью. Но если этот проводник свернуть в катушку, его индуктивность увеличится. При этом увеличится и сопротивление, оказываемое им переменному току, - ток в цепи уменьшится. С увеличением частоты тока индуктивное сопротивление катушки тоже увеличивается. Запомни: сопротивление катушки индуктивности переменному току возрастает с увеличением ее индуктивности и частоты проходящего по ней тока. Это свойство катушки используют в различных цепях приемников, когда требуется ограничить ток высокой частоты или выделить колебания высокой частоты, в выпрямителях переменного тока и во многих других случаях, с которыми вам придется постоянно сталкиваться на практике. Единицей индуктивности является генри (Гн). Индуктивностью 1Гн обладает такая катушка, у которой при изменении тока в ней на 1 А в течение 1 с развивается ЭДС самоиндукции, рав;ная 1 В. Этой единицей пользуются для определения индуктивности катушек, которые включают в цепи токов звуковой частоты. Индуктивность катушек, используемых в колебательных контурах, измеряют в тысячных долях генри, называемых миллигенри (мГн), или еще в тысячу раз меньшей единицей - микрогенри (мкГн).

МОЩНОСТЬ И РАБОТА ТОКА

На нагрев нити накала электрической или электронной лампы, электропаяльника, электроплитки или иного прибора затрачивается некоторое количество электроэнергии. Эту энергию, отдаваемую источником тока (или получаемую от него нагрузкой) в течение 1 с, называют мощностью тока. За единицу мощности тока принят ватт (Вт). Ватт - это мощность, которую развивает постоянный ток 1А при напряжении 1В. В формулах мощность тока обозначают латинской буквой Р (читается «пэ»). Электрическую мощность в ваттах получают умножением напряжения в вольтах на ток в амперах, т.е. P = UI. Если, например, источник постоянного тока напряжением 4,5 В создает в цепи ток 0,1 А, то мощность тока будет: р = 4,5 х 0,1 = 0,45 Вт. Пользуясь этой формулой, можно, например, подсчитать мощность, потребляемую лампочкой карманного фонаря, если 3,5 В умножить на 0,28 А. Получим около 1 Вт. Изменив эту формулу так: I = P/U, можно узнать ток, протекающий через электрический прибор, если известны потребляемая им мощность и подводимое к нему напряжение. Каков, например, ток, идущий через электрический паяльник, если известно, что при напряжении 220 В он потребляет мощность 40 Вт? I = P/I = 40/220 = 0,18 А. Если известны ток и сопротивление цепи, но неизвестно напряжение, мощность можно подсчитать по такой формуле: P = I2R. Когда же известны напряжение, действующее в цепи, и сопротивление этой цепи, то для подсчета мощности используют такую формулу: Р = U2/R. Но ватт - сравнительно небольшая единица мощности. Когда приходится иметь дело с электрическими устройствами, приборами или машинами, потребляющими токи в десятки, сотни ампер, используют единицу мощности киловатт (пишут кВт), равную 1000 Вт. Мощности электродвигателей заводских станков, например, могут составлять от нескольких единиц до десятков киловатт. Количественный расход электроэнергии оценивают ватт - секундой, характеризующей единицу энергии - джоуль. Расход электроэнергии определяют умножением мощности, потребляемой прибором, на время его работы в секундах. Если, например, лампочка электрического фонарика (ее мощность, как мы уже знаем, около 1 Вт) горела 25 с, значит, расход энергии составил 25 ватт - секунд. Однако ватт - секунда величина очень малая. Поэтому на практике используют более крупные единицы расхода электроэнергии: ватт - час, гектоватт - час и киловатт - час. Чтобы расход энергии был выражен в ватт - часах или киловатт - часах, нужно соответственно мощность в ваттах или киловаттах умножить на время в часах. Если, например, прибор потребляет мощность 0,5 кВт в течение 2 ч, то расход энергии составит 0,5 Х 2 = 1 кВт ч; 1 кВт ч энергии будет также израсходован, если цепь будет потреблять (или расходовать) мощность 2 кВт в течение получаса, 4 кВт в течение четверти часа и т.д. Электрический счетчик, установленный в доме или квартире, где вы живете, учитывает расход электроэнергии в киловатт - часах. Умножив показания счетчика на стоимость 1 кВт-ч (сумма в коп.), вы узнаете, на какую сумму израсходовано энергии за неделю, месяц. При работе с гальваническими элементами или батареями говорят об их электрической емкости в ампер - часах, которая выражается произведением значения разрядного тока на длительность работы в часах. Начальная емкость батареи 3336Л, например 0,5 Ач. Подсчитай: сколько времени будет батарея непрерывно работать, если разряжать ее током 0,28 А (ток лампочки фонаря)? Примерно один и три четверти часа. Если же эту батарею разряжать более интенсивно, например, током 0,5 А, она будет работать меньше 1 ч. Таким образом, зная емкость гальванического элемента или батареи и токи, потребляемые их нагрузками, можно подсчитать примерное время, в течение которого будут работать эти химические источники тока. Начальная емкость, а также рекомендуемый разрядный ток или сопротивление внешней цепи, определяющее разрядный ток элемента или батареи, указывают иногда на их этикетках или в справочной литературе.

В этом уроке я попытался систематизировать и выложить максимум необходимой для начинающего радиолюбителя информации по основам электротехники, без которых дальше нет смысла, что то, продолжать изучать. Урок, получился пожалуй самый продолжительный, но и самый важный. Советую отнестись к этому уроку более серьезно, обязательно заучить выделенные определения, если что то, непонятно, перечитывайте несколько раз, что бы вникнуть в суть сказанного. В качестве практической работы, можете поэксперементировать со схемами изображенными на рисунках, т. е. с батарейками лампочками и переменным резистором. Это пойдет вам на пользу. А вообще, в этом уроке, конечно же, весь упор нужно сделать не на практику, а на усвоение теории.

Переходим к следующему уроку !

www.radio-schemy.ru

КОМПЛЕКСНЫЕ ЧИСЛА В ЭЛЕКТРОТЕХНИКЕ | sibac.info

КОМПЛЕКСНЫЕ ЧИСЛА В ЭЛЕКТРОТЕХНИКЕ

Мангушев Виталий Иванович

студент 2 курса, факультет электроэнергетики и электротехники ДВФУ, г. Владивосток

E-mail: [email protected]

Дмух Галина Юрьевна

научный руководитель, канд. пед. наук, доцент кафедры алгебры, геометрии и анализа ДВФУ, г. Владивосток

В математике очень широко применяется решение задач с помощью комплексных чисел, но что такое комплексные числа и как они нашли себя в электротехнике?

Первоначально математики столкнулись с мнимой единицей i=, когда стало не хватать действительного числа, а именно при решении простейшего квадратного уравнения , где «p» и «q» — действительные числа. При вычислении его корней по всем известным формулам, математики еще до XVI века сталкивались с проблемой отрицательного корня. В действительности, никто не мог объяснить какой смысл следует придавать этому выражению и, в следствие, решили, что корень из отрицательного числа не имеет смысла. И это работало, было легко показать, что при отрицательном корне, решением было ни положительное число, ни отрицательное, ни нуль.

Однако в дальнейшем, при решении кубических уравнений отказываться от отрицательного корня уже было невозможно. В 1543 году несколько итальянских ученых выдвинули формулу «Кардано» позволяющую решать уравнения третьей степени вида:

, а именно: , где , она вполне рабочая, но при решении уравнений имеющих три различных действительных корня она не дает ожидаемого результата. Например, корнями уравнения легко доказать, являются числа 0,1,–1, но при решении уравнения методом, изложенным выше, результат удивляет: и как же получить из этого три нужных нам корня?

После этого математики пошли на изучение мнимых чисел, дали возможность им существовать. Затем было обнаружено, что многие громоздкие задачи в математике решаются гораздо проще, если пользоваться мнимыми числами. К.Ф. Гаусс предложил называть мнимые числа комплексными, что впоследствии прижилось.

С похожей проблемой ученые столкнулись при решении задач электротехники.

Описание электромагнитных процессов в цепях переменного тока сводится к решению множества интегралов, а решение их становится столь сложным, что взять их не пол силу даже опытным математикам. Определение крайне упростилось и стало более элегантно при применении комплексных чисел.

Из физики мы знаем, что переменным током называется ток, изменяющийся во времени. Из всех возможных форм периодических токов наибольшее распространение имеет синусоидальный ток, так как у него есть преимущество в плане экономии энергоресурсов.

Любая синусоидальная функция времени «a(t)» может быть однозначно задана тремя параметрами: амплитудой, частотой и начальной фазой. Ее формула для любого момента времени «t»: , где — максимальное значение функции или её амплитуда; – угловая частота, начальная фаза (угол функции в момент времени принятый за начало отсчета, т. е. при ), аргумент называется фаза или фазовый угол, он определяет значение функции в любой момент времени. В электрических цепях переменного тока синусоидальными функциями времени являются ток, падение напряжения и ЭДС:

В электротехнике принято обозначать мгновенные значения токов строчными буквами в виде: ; А амплитуду заглавной с нижним индексом «» : .

Так же существует действующий(эффективный) ток. По закону Джоуля-Ленца на участке тока сопротивлением «r», за время «T», соответствующее периоду тока «i», будет выделено количество тепла равное: , с другой стороны при постоянном токе на этом же участке выделится равное количество энергии: , если приравнять данные формулы, можно вывести действующее значение тока .

Отсюда — действующий ток это среднеквадратичное значение переменного тока. По аналогии можно рассчитать действующее значение напряжения и ЭДС, которые так же равняются среднеквадратичной своей соответствующей.

Рисунок 1. Представление синусоиды тока в виде вращающегося вектора

Из курса математики известно, что синусоидальная функция времени может быть представлена в виде вращающегося вектора длиной с угловой частотой . Положение этого вектора в начальный момент времени t = 0 должно составлять угол с осью абсцисс.

Наиболее удобная для проведения расчетов координатная система стала комплексная, так как вектор можно определить четырьмя различными формами записи:

· Алгебраическая форма: , надо заметить, что в математике знак мнимой части используется как «», но в электротехнике этим знаком обозначается ток, по этому было решено заменить его на «». Знак «» не говорит ни о каком-либо сложении, он только указывает на то, что мы объединяем два действительных числа в нечто единое. На комплексной плоскости «» и «» координаты конца вектора тока, по мнимой и действительной оси.

· Тригонометрическая форма: запись результата вещественной и мнимой части через модуль «» и аргумент «»

· Показательная форма: — получается путем применения формулы Эйлера к тригонометрической.

· Полярная форма: — запись, не использующаяся для расчетов.

Рассмотрим типичную задачу в электротехнике: сложение токов.

Включим в цепь переменного тока две параллельные ветви, содержащие некое сопротивление. Нам известны: амплитуда, частота и начальная фаза токов, равная нулю. ,

Рисунок 2. Токи в параллельных ветвях цепи переменного тока

По одному из главных постулатов электротехники, а именно по I-му закону Кирхгофа (Алгебраическая сумма токов в узле равна нулю ) , отсюда , графически это можно определить так:

Рисунок 3. Сложение синусоид тока

Как видно, это было легко, при фазе равной нулю решение такой задачи обуславливается сложением значения амплитуд в каждый момент времени. . Всё просто.

А теперь представим, что фаза у токов отличается. Например, равняется не нулю, а скажем, 30, попробуем проделать задачу тем же способом:

Рисунок 4. Синусоиды тока с разной фазой

Решение:

;

по формуле суммы углов:

Воспользуемся методом введения дополнительного угла, чтобы привести уравнение к виду: ;

Так как у нас есть составляющие: и, найдем и .

По основному тождеству тригонометрии: , значит:

Находим и через и :

Подставляем в :

Как видим, такая, простая на первый взгляд, задача переливается в уравнение, которое заставит посидеть и подумать «как же оно решается?», а ведь это самое наипростейшее усложнение.

Теперь рассмотрим эту задачу с применением комплексных чисел, мы уже знаем, что такое комплексное число и в состоянии перевести в него уравнение синусоиды тока.

Итак:

; ,

сложим:

Решение в 2 строки, а результаты те же.

Проверим это на векторной диаграмме:

Рисунок 5. Векторная диаграмма

Выводы: На этом простейшем примере хорошо видно как комплексные числа упростили решение. Сейчас же ни одна задача в электротехнике не решается без них. Мнимые числа необходимая составляющая электротехники.

Список литературы:

1.Балк М.Б., Балк Г.Д., Полухин А.А. «Реальные применения мнимых чисел» // изд. «Радянська школа», 1988 г — 5—16 с.

2.Голубев А.Н. Доктор техн. наук, профессор, «Лекция по ТОЭ № 3 — Представление синусоидальных величин с помощью векторов и комплексных чисел».

3.Ландсберг Г.С. Элементарный учебник физики, том 2. «Электричество и магнетизм», § 160 «Сложение токов при параллельном включении сопротивлений в цепь переменного тока» — 384—389 с.

4.Мацкевич И.Ю. «Высшая математика приложения в физике и электронике» учебно-методическое пособие// МГВРК Минск 2008 — 5—7 с.

sibac.info

мир электроники - Расчеты по электронике и электротехнике

категория

Этот раздел посвящен в основном теории электроники: расчеты, формулы и т.п....Например: как рассчитать нужное сечение провода при удаленном подключении с учетом падения напряжения, как самостоятельно рассчитать трансформатор, мощность трехфазного тока и так далее.Если что-то не получается- заходите на наш ФОРУМ- подумаем вместе!!

Радиотехнические расчеты начинающим

Радиотехнические расчеты начинающим: Закон ОмаРадиотехнические расчеты начинающим: Сложные цепиРадиотехнические расчеты начинающим: цепи переменного токаРадиотехнические расчеты начинающим: Нелинейные цепиРадиотехнические расчеты начинающим: RC-фильтрыРадиотехнические расчеты начинающим: что такое децибелы

Рекомендуем так-же скачать книгу Типовые расчеты по электрооборудованию

Прочие расчеты по радио и электротехнике

Расчеты по электронике

Последовательное включение диодовКак рассчитать сечение проводаРасчет гасящего конденсатораУпрощенный расчет трансформатораРасчет резонансной частоты колебательного контураУпрощенный расчет колебательного контураРасчет триггера Шмитта Расчет дифференциального усилителяРасчет фильтров напряженияРасчет радиаторов охлажденияРасчет выпрямителей напряженияРасчет числа витков катушки индуктивностиРасчет волнового сопротивления линииКак определить параметры коаксиального кабеляРасчёт светодиодного драйвера NCP3066Как рассчитать индуктивность катушки без сердечникаРасчет частоты генератора на основе микросхемы К176ИЕ12Формулы расчета частоты мультивибратора на КМОП микросхемеРасчет усилительных ступеней на полевом транзистореРасчет частоты среза многозвенных RC фильтровФормулы расчета частоты мультивибратора на логическом элементеУпрощенные формулы для расчета фильтров акустических систем

Расчеты по электротехнике

подключение электродвигателей по схеме звезда и треугольникУдельное сопротивление проводниковВключение 3-х фазного двигателя в однофазную сетьПрименение электролитических конденсаторов для включения трехфазного двигателя в однофазную сетьРасчет мощности трехфазного токаКак пересчитать обмотку релеКак увеличить КПД трансформатораТрехфазный электродвигатель в двухфазную сеть без потери мощности

Программы для самостоятельных расчетов

Программа для расчета трансформатораПрограмма для расчета диодного мостаПрограмма для расчета предохранителяПрограмма для расчета катушки индуктивности

radio-uchebnik.ru