Приведение параметров вторичной обмотки и схема замещения приведенного трансформатора. Приведение параметров вторичной обмотки трансформатора к первичнойПриведение вторичной обмотки к первичной.Так как в общем случае w2w1,то Е2Е1иI2I1,то различны и параметры обмоток, т.е. их активные и индуктивные сопротивления, что затрудняет количественный учет процессов, происходящих в трансформаторах, и построение векторных диаграмм. Чтобы избежать этих трудностей, обе обмотки трансформатора приводятся к одному числу витков. Обычно приводят вторичную обмотку к первичной, имеющую такое же количество витков, с условием, чтобы эта операция приведения не отразилась на энергетическом процессе. При этом число витков вторичной обмотки изменяется в «k» раз
В результате такого приведения 2=k2; 2=k2. (14-21) Чтобы мощность приведенной и реальной обмоток при всех режимах работы были равны, необходимо соблюдать равенство22= 22, где наведенный вторичный ток 2= 2/k. (14-22) Намагничивающие силы приведенной и реальной обмоток 22=22(14-23) Суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка, должно уменьшаться в k-раз. Но поскольку приведенная обмотка имеет вk-раз больше витков, то r2=k2r2(14-24) x2=k2x2(14-25) Очевидно, что потери в приведенной и реальной обмотках одинаковы:
Одинаковы также относительные падения напряжения во вторичных обмотках приведенного и реального трансформаторов:
Схема замещения без учета магнитных потерь. Сделаем в уравнениях (14-14) подстановки: (14-26) Умножив при этом второе уравнение (14-14) на k, получим (14-27) При переходе к электрической связи двух цепей в соответствующей схеме замещения должна появится общая для обеих цепей ветвь, которая обтекается суммой токов обеих цепей İ1+İ2. Соответственно этому, в уравнениях напряжений этих цепей должны появиться одинаковые члены с множителями (I1+İ2). Из уравнений (14-27) видно, что для получения в них таких членов нужно прибавить к первому уравнению и вычесть из него членjkx12I2. При этом: (14-28) Введем следующие наименования и обозначения - приведенное активное сопротивление вторичной обмотки r2=k2 r 2 (14-29) - приведенное взаимное индуктивное сопротивление x12=kx12; (14-30) - индуктивное сопротивление рассеяния первичной обмотки x1=x11-kx12; (14-31) - приведенное индуктивное сопротивление рассеяния вторичной обмотки, (14-32) где (14-33) представляет собой непреведенное индуктивное сопротивление вторичной обмотки. В результате подстановок в (14-28) получим следующие уравнения напряжений приведенного трансформатора:
(14-34) Этим уравнениям соответствует схема замещения рис. 14-3, а. Аналогичным образом можно также преобразовать уравнения напряжения в дифференциальной форме (14-13), произведя в них подстановки u2=u2/k;i2=ki2(14-35). При этом получается схема замещения рис. 14-3, б, где: (14-36) (14-37) S1иS2представляют собой индуктивности рассеяния первичной и вторичной обмоток, а (14-38) приведенную взаимную индуктивность.
Рис. 14-3. Схемы замещения двухобмоточного трансформатора без учета магнитных потерь (Т-образные): а) – в комплексной форме б) – в дифференциальной форме. По уравнениям (14-34) и схеме замещения рис. 14-3 получается идеальный трансформатор, у которого приведенные собственные взаимные индуктивные сопротивления одинаковы и равны и поэтому с2= 1 и= 0 Параметры схемы замещения по рис. 14-3. При : Приведенная взаимная индуктивность:
или на основании (14-4) (14-39) Последний член (14-39) весьма мал по сравнению с первым, поэтому с достаточной точностью (14-40) Соответственно, согласно выражениям x11=L11;x22=L22;x12=M;x12=kx12; и M12=Lc1,,, или (14-41) Следовательно, сопротивление x12с большой точностью равно сопротивлению самоиндукции первичной обмотки от потока, замыкающегося по магнитопроводу. Ветви 1-2 схем замещения называются намагничивающими ветвями; их ток: , создает результирующую намагничивающую силу обмоток трансформатора: , которая в свою очередь создает результирующий поток стержня с амплитудой Фс. Напряжение на этих ветвях: , т. е. равно по значению и обратно по знаку э.д.с. Е1, которая индуктируется в первичной обмотке результирующим потоком магнитопровода и отстает от него на 90. Индуктивности рассеяния обмоток (без математических выкладок): (14-42) (14-43) Таким образом, индуктивности рассеяния S1,S2иS2и индуктивные сопротивления рассеяния x1=S1;x2=S2;x2=S2, (14-44) при , определяются магнитным потоком, замыкающимся главным образом по воздуху. Однако вторыми членами равенств (14-42) и (14-43) по сравнению с первыми, пренебречь нельзя, и поэтому потоки, замыкающиеся по воздуху можно назвать потоками рассеяния лишь условно. Схема замещения с учетом магнитных потерь. Потери в стали магнитопровода Рмгпри заданной частоте пропорциональны величинам: РмгВ2сФ2сЕ21U212, т.е. пропорциональны квадрату напряжения U12на зажимах 1-2 намагничивающей цепи схемы замещения рис. 14-3, а. Если к этим зажимам параллельно х12= хс1 подключить активное сопротивлениеrмг, то потери в этом сопротивлении будут также пропорциональныU212. Значение сопротивленияrмгможно подобрать так, чтобы потери в нем равнялись магнитным потерям : (14-45)Отсюда:
Рис. 14-4. Намагничивающая цепь с учетом магнитных потерь. где m1– коэффициент подбора. Намагничивающий ток M=1+2, разделяется в двух ветвях намагничивающей цепи на активную МАи реактивную МГсоставляющие, из которых первая определяет мощность магнитных потерь, а вторая создает поток магнитопровода. Однако, расчеты вести удобнее, если объединить две параллельные ветви в одну общую ветвь. Тогда: . (14-46) Так как rмгx12,то ; , (14-47) При увеличении насыщения магнитопровода, т.е при увеличении Фс, Е1илиU1, приведенное индуктивное сопротивлениеx12приf=constуменьшается. Однако, при этомrмг const, а значениеrMуменьшается. Схема замещения с учетом магнитных потерь согласно рис. 14-4, б показана на рис. 14-5, а. Если использовать обозначения: (14-48), то схему замещения можно использовать проще (рис.14-5, б).
Рис. 14-5. Схема замещения двухобмоточного трансформатора с учетом магнитных потерь. В режиме холостого хода и - току холостого хода. В итоге получилась весьма простая Т-образная схема замещения трансформатора, представляющая собой пассивный четырехполюсник. Сопротивление намагничивающей цепи этой схемы zмотражает явления в ферромагнитном магнитопроводе. Оно значительно больше сопротивленияZ1иZ2, которые включают в себя активные сопротивления и индуктивные сопротивления рассеяния обмоток. Для силовых трансформаторов в относительных единицахZм*= 25200;z1*z2*= 0.0250.10. Уравнения напряжений и схему замещения трансформатора можно представить также в относительных единицах, имея в виду что Uн=zнIн. Упрощенная схема замещения. Поскольку zмz1z2, то можно положить во многих случаяхzм=, что означает разрыв намагничивающей цепи схемы замещения, т.е.Iм= 0, что аналогично пренебрежению намагничивающим током или током холостого хода, что в ввиду малости во многих случаях допустимо. При этом
При zм=иIм= 0 схема замещения принимает вид, изображенный на рис. 14-6. Параметры этой схемы: (14-49)
Рис. 14-6. Упрощенная схема замещения трансформатора называются соответственно: полным, активным и индуктивным сопротивлениями короткого замыкания. Обычно в силовых трансформаторах zk*= 0,050,15. Замыкание вторичных зажимов трансформатора накоротко, соответствует замыканию накоротко вторичных (правых) зажимов схемы замещения и при этом сопротивление трансформатора будет равным zк. §14-4. Определение параметров схемы замещения трансформатора. Могут быть определены расчетным и опытным путем. Расчетное определение: Активные сопротивления обмотоклегко рассчитываются по обмоточным данным, если известныкоэффициенты вытеснения тока, учитывающие увеличение активных сопротивлений под влиянием поверхностного эффекта. Обычно эти коэффициенты находятся в пределах 1,0051,15. Параметры намагничивающей цепилегко определяются по данным расчета магнитной цепи по закону полного тока
или на основании вычисления энергии магнитного поля магнитопровода или его намагничивающей (реактивной) мощности (см. §13-2). (14-45). Чтобы найти х12для заданного значения э.д.с. (12-3) надо определить поток Фс, затем намагничивающую силуFпо формулам (13-1) и (13-2) , (13-1) где: nф– число стыков магнитопровода,- величина зазора для шихтованных магнитопроводов= 0,0030,005мм. Действующее значение основной гармоники намагничивающего тока , (13-3) где w- число витков обмотки,k– коэффициент, учитывающий наличие высших гармоник в магнитопроводе: при Вст= 1Тk= 1,5 и Вст= 1,4Тk= 2,2. Магнитная характеристика показана на рис. 13-1. Тогда: . Метод противовключения. Наибольшую трудность, вследствие сложного характера магнитных полей в воздухе, представляет определение индуктивных сопротивлений рассеяния х1и х2, имеющих важное значение, влияние которых на эксплуатационные показатели и характеристики трансформатора гораздо больше, чем влияние параметров намагничивающей цепи. Для вычисления х1и х2используется метод противовключения (метод Роговского в 1909 г.), который состоит в том, что: если питать трансформатор с первичной и вторичной сторон такими напряжениями, что,то поток Фс= 0 и Е1= Е2= 0. Намагничивающие силы первичной и вторичной обмоток при этом равны по значению и противоположны по знаку F1= -F2, откуда и происходит название метода. Если измерить U1,U2,I1,I2и мощностиP1иP2, то можно определить параметры , где m– число фаз. и, наконец, сопротивления рассеяния
В связи с изложенным можно сказать, что в режиме противовключения существуют только магнитные поля рассеяния. Идея метода противовключения лежит в основе всех расчетных методов определения индуктивных сопротивлений рассеяния. При w1w2осуществление опыта Роговского практически невозможно, так как в магнитопроводе даже при небольшом нарушении условия: возникает заметный поток Фс, сравнимый с потоком в воздухе Фв. Поэтому опыт проводят на макетах сw1=w2 или при замене вторичной обмотки приведенной. В силу значительных трудностей обычно рассчитывается сумма индуктивных сопротивлений рассеяния, исходя из картины магнитного поля в режиме противовключения, когда и все магнитные линии направлены вертикально вверх и их длинаll - коэффициент Роговского, где l- высота стержня магнитопро-вода;l– высота катушки. §14-5. Опытное определение параметров схемы замещения трансформатора. Определяются по данным опыта холостого хода и короткого замыкания.
Рис. 14-10. Схема опыта холостого хода однофазного трансформатора. Измеряемые величины очевидны из рис.14-10. Из данных опыта холостого хода (О.Х.Х) определяются: - полное, активное и индуктивное сопротивления х.х. ; (14-60) - коэффициент трансформации (14-61) - коэффициент мощности х.х. (14-62) ; (14-70) в действительности z1Ioможно пренебречь и положить .
Рис. 14-11. Векторная диаграмма трансформатора при холостом ходе. Для трехфазного трансформатора при соединении первичной обмотки в звезду (14-63) а при соединении ее в треугольник: (14-64) Коэффициент мощности холостого хода: (14-65) Целесообразно определять относительные значения перечисленных сопротивлений. Из схемы замещения при холостом ходе следует (14-68) В силовых трансформаторах r1иx1в десятки, сотни раз меньшеrMиxM. Поэтому с большой точностью можно считать, что параметры холостого хода равны параметрам намагничивающей цепи: zo = zM; ro = rM; xo = xM, (14-69) и мощность холостого хода Ро Рмг– магнитным потерям в магнитопроводе, а (14-71) Вследствие преобладания индуктивного сопротивления при Uo=Uнкоэффициент мощностиcosφ≤ 0,1. Так как r1<<rM, то потери холостого хода практически представляют собой потери в стали магнитопровода, включая потери от вихревых токов в стенках бака. Опыт холостого хода производят обычно для ряда значений Uo: отUo0,3UндоUo1,1Uни по полученным данным строят характеристики холостого хода:I,Po,zo,ro,cosφo=(Uo). Опыт короткого замыкания.
Рис. 14-13. Схема опыта короткого замыкания. Вторичная обмотка замыкается накоротко, а к первичной подводится пониженное напряжение, чтобы I1≤Iн. При этом: (14-72) Для трехфазного трансформатора по показаниям приборов определяются средние значения линейного напряжения Uк.л., линейного токаIк.л.и мощности короткого замыкания Рк. Напряжение Uк=Uк.н, при котором ток короткого замыкания равен номинальному:I=Iн, носит названиенапряжения короткого замыканияи обозначается «Uк». Величина Uк в относительных единицах равна сопротивлению короткого замыкания в относительных единицах (14-77) Величина выражается на практике также в процентах: (14-78) Векторная диаграмма трансформатора при коротком замыкании с Iк=Iнизображена в двух видах на рис. 14-15, а, б. Треугольник на рис. 14-15, б называетсятреугольником короткого замыкания.Его катеты представляют собой активную и реактивную составляющие напряжения короткого замыкания: (14-79)
Рис. 14-15. Векторные диаграммы трансформатора при коротком замыкании с Iк = Iн. В трансформаторах мощностью Sн= 10кВА обычноcosφk0,65, а приSн= 60кВА обычноcosφk0,05, т.е. в мощных трансформаторах преобладают составляющиеukrиxkпо сравнению сukaиrk.Значениеuka*приводится к температуре обмоток 75°С. Напряжение короткого замыкания ukхарактеризует значение активных сопротивленийrи индуктивных сопротивлений рассеянияxтрансформатора, и является поэтому важной характеристикой трансформатора. Значениеuk% указывается в паспортной табличке трансформатора. В силовых трансформаторахuk%= 4,515. Первая цифра относится к трансформаторам с номинальным линейным напряжениемUлн≤ 10 кВ, а вторая – сUлн= 500 кВ, которые обладают большим рассеянием между обмотками. Значение э.д.с. Е1в опыте короткого замыкания приIк=Iн в 1540 раз меньшеUн. При этом магнитные потери в 2251600 раз меньше, чем в случаеU=Uн, и весьма малы.Поэтому мощность короткого замыкания Ркс большой точностью представляет собой мощность электрических потерь в обмотках, включая добавочные потери в стенках бака и в крепежных деталях от потоков рассеяния. Следовательно, иrk=r1+r2, определенное из опыта короткого замыкания, является эквивалентным сопротивлением с учетом этих потерь. Если короткое замыкание происходит при номинальном первичном напряжении, то , или в относительных единицах Если, например, uk% = 10%, тоIк =10Iн; uk%= 4,5%, тоIк=22,2Iн; uk%= 15%, тоIк=6,7Iн. studfiles.net Приведение вторичной обмотки трансформатора к первичнойПри такой трактовке функций обмоток ЭДС В комплексной форме уравнения, составленные по второму закону Кирхгофа, запишутся: для первичной обмотки
для вторичной обмотки
где
6.4. Приведение вторичной обмотки трансформатора к первичной. При расчете электрической цепи с трансформатором задача расчета усложняется из-за магнитной связи первичной и вторичной обмоток трансформатора. Для устранения магнитной связи составляется эквивалентная электрическая схема, когда обе обмотки объединяют в одну, сделав равными ЭДС ( Для него МДС, относительные значения падений напряжения и мощность потерь в проводах остается неизменным, т. е.
Математически приведенный трансформатор описывается уравнениями электрического состояния
и уравнением токов. Уравнение токов получим из уравнения МДС для мгновенных значений
где F – мгновенное значение результирующей МДС обеих обмоток. При неизменном напряжении на первичной обмотке U1, магнитный поток Ф практически неизменен в режимах холостого хода до номинального. Поэтому можно записать, что
или в комплексном виде
Разделив обе части уравнения на w1 и обозначив
В соответствии с этими уравнениями схема замещения трансформатора выглядит следующим образом (рис. 6.3)
Рис. 6.3 На представленной схеме R1 и Из-за трудности экспериментального определения параметров схемы замещения для расчетов можно использовать упрощенную схему замещения (если пренебречь током холостого хода) (рис. 6.4)
Рис. 6.4 В этой схеме Rk и Xk – сопротивления короткого замыкания 6.1.5. Мощность потерь и КПД трансформатора Уравнение баланса мощности в цепи с трансформатором
где КПД трансформатора
Так как коэффициент нагрузки
fiziku5.ru § 1.6. Приведение параметров вторичной обмотки и схема замещения приведенного трансформатораВ общем случае параметры первичной обмотки трансформатора отличаются от параметров вторичной обмотки. Эта разница наиболее ощутима при больших коэффициентах трансформации, что затрудняет расчеты и построение векторных диаграмм, так как в этом случае векторы электрических величин первичной обмотки значительно отличаются по своей длине от одноименных векторов вторичной обмотки. Указанные затруднения устраняются приведением всех параметров трансформатора к одинаковому числу витков, обычно к числу витков первичной обмотки w1. С этой целью все величины, характеризующие вторичную цепь трансформатора, — ЭДС, напряжение, ток и сопротивления — пересчитывают на число витков w1 первичной обмотки. Таким образом, вместо реального трансформатора с коэффициентом трансформации k = w1/w2 получают эквивалентный трансформатор с k=w1/w’2=1, где w’2=w1. Такой трансформатор называют приведенным. Однако приведение вторичных параметров трансформатора не должно отразиться на его энергетических показателях: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе. Так, электромагнитная мощность вторичной обмотки реального трансформатора Е2I2 должна быть равна электромагнитной мощности вторичной обмотки приведенного трансформатора: (1.27) Подставив значение приведенного тока вторичной обмотки I2 = I2(w2/w1,) в (1.27), получим формулу приведенной вторичной ЭДС: (1.28) Так как U2I2 ≈U’2I’2, то приведенное напряжение вторичной обмотки (1.29) Из условия равенства потерь в активном сопротивлении вторичной обмотки имеем . Определим приведенное активное сопротивление: (1.30) Приведенное индуктивное сопротивление рассеяния вторичной обмотки определяют из условия равенства реактивных мощностей , откуда (1.31) Приведенное полное сопротивление вторичной обмотки трансформатора (1.32) Приведенное полное сопротивление нагрузки, подключенной на выводы вторичной обмотки, определим по аналогии с (1.32): (1.33) Уравнения напряжений и токов для приведенного трансформатора имеют вид (1.34) Эти уравнения устанавливают аналитическую связь между параметрами трансформатора во всем диапазоне нагрузок от режима х.х. до номинальной. Еще одним средством, облегчающим исследование электромагнитных процессов и расчет трансформаторов, является применение электрической схемы замещения приведенного трансформатора. На рис. 1.18, а представлена эквивалентная схема приведенного трансформатора, на которой сопротивленияr и х условно вынесены из соответствующих обмоток и включены последовательно им. Как было установлено ранее, в приведенном трансформатореk = 1, а поэтому . В результате точкиА и а, а также точкиX их на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 1.18,б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.
Рис. 1.18. Эквивалентная схема (в) и схема замещения (б) приведенного Схема замещения приведенного трансформатора удовлетворяет всем уравнениям ЭДС и токов приведенного трансформатора (1.34) и представляет собой совокупность трех ветвей: первичной — сопротивлениемZ1=r1+jx1 и током;намагничивающей — сопротивлениемZm=rm+jxm и током;вторичной — с двумя сопротивлениями: сопротивлением собственно вторичной ветвиZ'2 =r’2 + jx'2 и сопротивлением нагрузкиZ'H = rн' ±jx'H и током. Изменением сопротивления нагрузкиZ'H на схеме замещения могут быть воспроизведены все режимы работы трансформатора. Параметры ветви намагничивания Zm = rm + jxm определяются током х.х. Наличие в этой ветви активной составляющейrm обусловлено магнитными потерями в трансформаторе (см. § 1.14). Все параметры схемы замещения, за исключением Z'H, являются постоянными для данного трансформатора и могут быть определены из опыта х.х. и опыта к.з. (см. §1.11). studfiles.net Приведение обмоток трансформатораПри изучении и анализе режимов работы трансформатора, задача затрудняется тем, что коэффициент трансформации k может иметь относительно большое значение, в связи с чем, возникают трудности с построением векторной диаграммы трансформатора. Проблема решается приведением числа витков вторичной обмотки к числу первичной. Таким образом, коэффициент трансформации станет
Для трансформатора, у которого параметры вторичной обмотки пересчитаны под число витков первичной (приведенного), справедливы следующие уравнения
Определим составляющие этих уравнений, учитывая что, приведение не должно изменить режим работы первичной цепи и энергетические параметры вторичной цепи должны остаться прежними. При приведении не должна измениться намагничивающая сила вторичной обмотки поэтому
Исходя из того, что электромагнитная мощность вторичной обмотки не должна изменится, найдем приведенную ЭДС вторичной обмотки E’2
Приведенное напряжение вторичной обмотки
Приведенное активное сопротивление, находят при условии равенства потерь во вторичной обмотке
Аналогично находится приведенное индуктивное сопротивление вторичной обмотки при равенстве реактивных мощностей
Приведенное полное сопротивление
Приведенное полное сопротивление нагрузки
Ток I0 – это ток холостого хода, который определяется из опыта холостого хода трансформатора. Читайте также - Схема замещения трансформатора electroandi.ru Приведение вторичной обмотки трансформатора к первичной. — КиберПедияПриведение вторичной обмотки трансформатора к первичной. Первичные и вторичные токи, напряжения и другие величины имеют одинаковый порядок, если первичной и вторичной обмоток число витков одинаково. Рассмотрим поэтому вместо реального трансформатора эквивалентный ему так называемый приведенный трансформатор, первичные и вторичные обмотки которого имеют одинаковое число витков. Представим себе, что реальная вторичная обмотка трансформатора с числом витков Величина k называется коэффициентом приведения или трансформации. В результате такой замены, или приведения, э. д. с.
Чтобы мощности приведенной н реальной обмоток при всех режимах работы были равны, необходимо изменить вторичный ток в к раз.
Намагничивающие силы приведенной и реальной обмоток равны:
Для того чтобы электромагнитные процессы в реальном и приведенном трансформаторах протекали одинаково, приведенная и реальная вторичные обмотки должны создавать одинаковые магнитные поля. Для этого), необходимо, чтобы приведенная вторичная обмотка имела те же геометрические размеры и конфигурацию и была расположена в окне магнитопровода трансформатора так же, как и реальная вторичная обмотка. Поэтому суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка приведенной обмотки должно уменьшиться в к раз. Но поскольку приведенная обмотка имеет в k раз больше витков, то в итоге активное сопротивление приведенной обмотки в к2 раз больше, чем реальной:
Так как при одинаковых геометрических размерах и одинаковом расположении катушек их индуктивности и индуктивные сопротивления пропорциональны квадратам чисел витков, то между индуктивными сопротивлениями приведенной обмотки
Потери в приведенной н реальной обмотках одинаковы:
Одинаковы также относительные падения напряжения во вторичных обмотках приведенного и реального трансформаторов:
Таким образом, все энергетические и электромагнитные соотношения в приведенном и реальном трансформаторах одинаковы, что и позволяет производить указанное приведение.
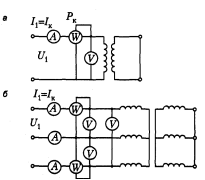
Опыт холостого хода. Схемы опытов холостого хода однофазного (m = 1) и трехфазного (m = 3) двухобмоточных трансформаторов приведены на рис. 14.3.
Первичная обмотка трансформатора подключается к синусоидальному напряжению, а вторичная обмотка разомкнута. Измеряются первичные напряжения На основе данных опыта для однофазного трансформатора определяются полное, активное и индуктивное сопротивления холостого хода:
а также коэффициент трансформации
и коэффициент мощности при холостом ходе
Для трехфазного трансформатора по показаниям трех амперметров и вольтметров определяются средние значения линейного тока
а при соединении ее в «треугольник•
Коэффициент мощности при холостом ходе
Коэффициент трансформации трехфазного трансформатора может рассчитываться по фазным напряжениям (k) или линейным напряжениям (kл)· Для теории трансформатора имеет значение первое из указанных значений коэффициента трансформации. Из рассмотрения схемы замещения трансформатора при
Мощность холостого хода При холостом ходе, согласно схеме замещения, Опыт короткого замыкания. Производится по схемам, приведенным на рис. 14.6 . Вторичные обмотки замыкаются накоротко, а к первичным обмоткам во избежание перегрева и повреждения трансформатора подводится пониженное напряжение с таким расчетом, чтобы ток находился в пределах номинального. Полное zк, активное rк и реактивное хк сопротивления короткого замыкания рассчитываются по формулам, аналогичным для случая холостого хода. Для однофазного трансформатора
В случае трехфазного трансформатора по показаниям приборов определяются средние значения линейного напряжения
а при соединении первичной обмотки треугольником:
Коэффициент мощности при коротком замыкании определяется по формулам, аналогичным при ХХ. Согласно схеме замещения
Приведение вторичной обмотки трансформатора к первичной. Первичные и вторичные токи, напряжения и другие величины имеют одинаковый порядок, если первичной и вторичной обмоток число витков одинаково. Рассмотрим поэтому вместо реального трансформатора эквивалентный ему так называемый приведенный трансформатор, первичные и вторичные обмотки которого имеют одинаковое число витков. Представим себе, что реальная вторичная обмотка трансформатора с числом витков Величина k называется коэффициентом приведения или трансформации. В результате такой замены, или приведения, э. д. с.
Чтобы мощности приведенной н реальной обмоток при всех режимах работы были равны, необходимо изменить вторичный ток в к раз.
Намагничивающие силы приведенной и реальной обмоток равны:
Для того чтобы электромагнитные процессы в реальном и приведенном трансформаторах протекали одинаково, приведенная и реальная вторичные обмотки должны создавать одинаковые магнитные поля. Для этого), необходимо, чтобы приведенная вторичная обмотка имела те же геометрические размеры и конфигурацию и была расположена в окне магнитопровода трансформатора так же, как и реальная вторичная обмотка. Поэтому суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка приведенной обмотки должно уменьшиться в к раз. Но поскольку приведенная обмотка имеет в k раз больше витков, то в итоге активное сопротивление приведенной обмотки в к2 раз больше, чем реальной:
Так как при одинаковых геометрических размерах и одинаковом расположении катушек их индуктивности и индуктивные сопротивления пропорциональны квадратам чисел витков, то между индуктивными сопротивлениями приведенной обмотки
Потери в приведенной н реальной обмотках одинаковы:
Одинаковы также относительные падения напряжения во вторичных обмотках приведенного и реального трансформаторов:
Таким образом, все энергетические и электромагнитные соотношения в приведенном и реальном трансформаторах одинаковы, что и позволяет производить указанное приведение.
cyberpedia.su
megapredmet.ru Приведение параметров вторичной обмотки и схема замещения приведенного трансформатора
В общем случае параметры первичной обмотки трансформатора отличаются от параметров вторичной обмотки. Эта разница наиболее ощутима при больших коэффициентах трансформации, что затрудняет расчеты и построение векторных диаграмм, так как в этом случае векторы электрических величин первичной обмотки значительно отличаются по своей длине от одноименных векторов вторичной обмотки. Указанные затруднения устраняются приведением всех параметров трансформатора к одинаковому числу витков, обычно к числу витков первичной обмотки w1. С этой целью все величины, характеризующие вторичную цепь трансформатора, – ЭДС, напряжение, ток и сопротивления – пересчитывают на число витков w1 первичной обмотки с учётом коэффициентом трансформации Так, электромагнитная мощность вторичной обмотки реального трансформатора Е2I2 должна быть равна электромагнитной мощности вторичной обмотки приведенного трансформатора:
Подставив значение приведенного тока вторичной обмотки
Так как
Из условия равенства потерь в активном сопротивлении вторичной обмотки имеем
Приведенное индуктивное сопротивление рассеяния вторичной обмотки определяют из условия равенства реактивных мощностей
Приведенное полное сопротивление вторичной обмотки трансформатора
Приведенное полное сопротивление нагрузки, подключенной на выводы вторичной обмотки, определим по аналогии с (1.32):
Уравнения напряжений и токов для приведенного трансформатора имеют вид
Эти уравнения устанавливают аналитическую связь между параметрами трансформатора во всем диапазоне нагрузок от режима х.х. до номинальной. Еще одним средством, облегчающим исследование электромагнитных процессов и расчет трансформаторов, является применение электрической схемы замещения приведенного трансформатора. На рис. 33, а представлена эквивалентная схема приведенного трансформатора, на которой сопротивления r и x условно вынесены из соответствующих обмоток и включены последовательно им. В приведенном трансформаторе k = 1, а поэтому
Рис. 33. Эквивалентная схема (а) и схема замещения (б) приведенного трансформатора
Схема замещения приведенного трансформатора удовлетворяет всем уравнениям ЭДС и токов приведенного трансформатора (1.34) и представляет собой совокупность трех ветвей: первичной – сопротивлением Параметры ветви намагничивания Все параметры схемы замещения, за исключением
Похожие статьи:poznayka.org |
|
|||||||||||||||||
|
|
|||||||||||||||||
|




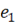 направлена против положительного направления тока
направлена против положительного направления тока 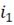 , а положительное направление тока
, а положительное направление тока 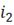 вторичной обмотки совпадает по направлению с ЭДС
вторичной обмотки совпадает по направлению с ЭДС 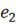 .
.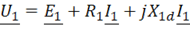 ,
,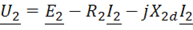 ,
,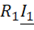 ,
, 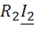 — падение напряжения на активных сопротивлениях первичной и вторичной обмоток соответственно;
— падение напряжения на активных сопротивлениях первичной и вторичной обмоток соответственно;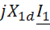 ,
, 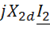 – падение напряжения на сопротивлениях рассеяния первичной и вторичной обмоток соответственно.
– падение напряжения на сопротивлениях рассеяния первичной и вторичной обмоток соответственно.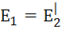 ) этих обмоток. Равенство будет выполнено, если число витков вторичной обмотки
) этих обмоток. Равенство будет выполнено, если число витков вторичной обмотки 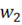 сделать равным числу витков первичной обмотки
сделать равным числу витков первичной обмотки 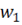 , т. е.
, т. е. 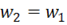 . При этом необходимо пересчитать все величины вторичной обмотки – привести вторичную обмотку к числу витков первичной обмотки, в этом случае трансформатор называется приведенным.
. При этом необходимо пересчитать все величины вторичной обмотки – привести вторичную обмотку к числу витков первичной обмотки, в этом случае трансформатор называется приведенным.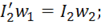
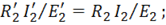
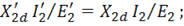
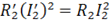
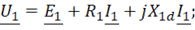
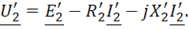
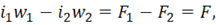
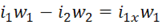
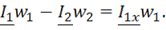
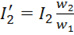 , получим уравнение токов
, получим уравнение токов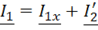
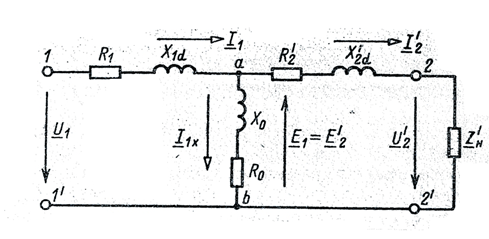
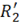 – активные сопротивления первичной и вторичной обмоток; X1d и
– активные сопротивления первичной и вторичной обмоток; X1d и 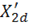 – сопротивления рассеяния первичной и вторичной обмоток; R0, X0 – активное и реактивное сопротивления ветви холостого хода. Падение напряжения на ветви холостого хода с комплексным сопротивлением
– сопротивления рассеяния первичной и вторичной обмоток; R0, X0 – активное и реактивное сопротивления ветви холостого хода. Падение напряжения на ветви холостого хода с комплексным сопротивлением 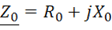 при токе
при токе 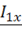 равно ЭДС
равно ЭДС 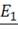 и
и 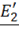 трансформатора.
трансформатора.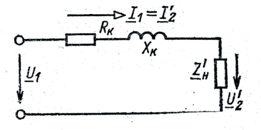
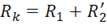 и
и 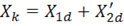 .
.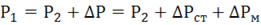 ,
,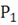 – активная мощность поступающая от источника,
– активная мощность поступающая от источника, 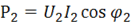 – активная мощность потребителя;
– активная мощность потребителя; 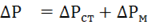 — суммарная мощность потерь в трансформаторе;
— суммарная мощность потерь в трансформаторе; 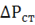 – мощность потерь в стали;
– мощность потерь в стали; 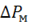 – мощность потерь в проводах обмотки.
– мощность потерь в проводах обмотки.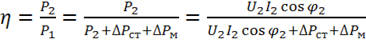 .
.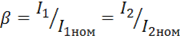 , а из опытов короткого замыкания и холостого хода получено, что
, а из опытов короткого замыкания и холостого хода получено, что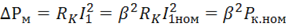









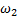 заменена воображаемой, или приведенной, обмоткой с числом витков
заменена воображаемой, или приведенной, обмоткой с числом витков 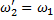 . При этом число витков вторичной обмотки изменится в
. При этом число витков вторичной обмотки изменится в 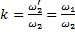 раз.
раз.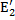 , и напряжение
, и напряжение 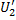 приведенной обмотки также изменяются в k раз по сравнению с величинами
приведенной обмотки также изменяются в k раз по сравнению с величинами 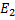 и
и 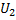 реальной вторичной обмотки:
реальной вторичной обмотки: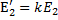 ;
; 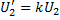 ;
;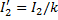
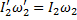
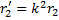
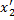 и реальной
и реальной 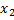 существует такое же соотношение:
существует такое же соотношение: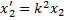
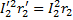
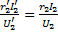 ;
; 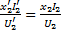 ;
;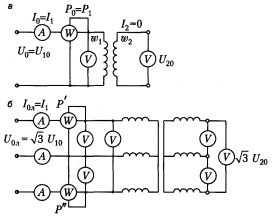
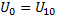 , ток
, ток 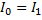 и мощность
и мощность 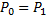 , а также вторичное напряжение
, а также вторичное напряжение 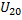 .
.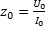 ;
; 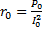 ;
; 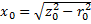
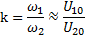
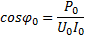
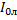 и линейного напряжения
и линейного напряжения 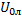 а по показаниям ваттметров - мощность холостого хода трех фаз,
а по показаниям ваттметров - мощность холостого хода трех фаз, 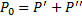 . Физический смысл имеют только значения сопротивлений, рассчитанные для фазы обмотки, поэтому необходимо принимать во внимание схему соединения обмотки. В случае соединения первичной обмотки в «звезду•
. Физический смысл имеют только значения сопротивлений, рассчитанные для фазы обмотки, поэтому необходимо принимать во внимание схему соединения обмотки. В случае соединения первичной обмотки в «звезду•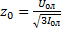 ;
; 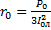 ;
; 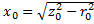
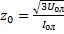 ;
; 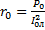 ;
; 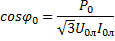
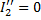 следует, что параметры холостого хода z0, r0, х0 представляют собой суммы следующих сопротивлений:
следует, что параметры холостого хода z0, r0, х0 представляют собой суммы следующих сопротивлений: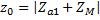 ;
; 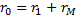 ;
; 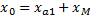
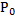 с весьма большей точностью соответствует магнитным потерям
с весьма большей точностью соответствует магнитным потерям 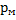 в сердечнике трансформатора.
в сердечнике трансформатора.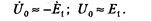
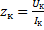 ;
; 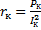 ;
; 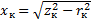
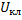 , линейного тока
, линейного тока 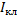 и мощности короткого замыкания трех фаз Рк. При соединении первичной обмотки в •звезду• параметры короткого замыкания на фазу будут следующими:
и мощности короткого замыкания трех фаз Рк. При соединении первичной обмотки в •звезду• параметры короткого замыкания на фазу будут следующими: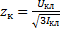 ;
; 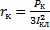 ;
; 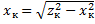
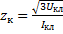 ;
; 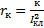 ;
; 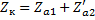 ;
; 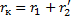 ;
; 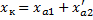


 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.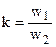 , трансформатор с
, трансформатор с 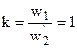 , где
, где 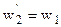 . Такой трансформатор называют приведенным. При этом его энергетические показатели: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе.
. Такой трансформатор называют приведенным. При этом его энергетические показатели: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе.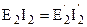 . (1.27)
. (1.27)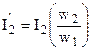 в (1.27), получим формулу приведенной вторичной ЭДС:
в (1.27), получим формулу приведенной вторичной ЭДС: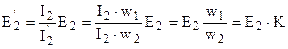 . (1.28)
. (1.28)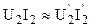 , то приведенное напряжение вторичной обмотки
, то приведенное напряжение вторичной обмотки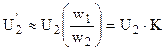 . (1.29)
. (1.29)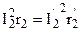 . Определим приведенное активное сопротивление:
. Определим приведенное активное сопротивление: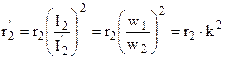 . (1.30)
. (1.30)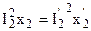 откуда
откуда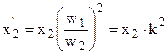 . (1.31)
. (1.31)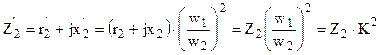 . (1.32)
. (1.32)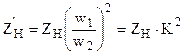 . (1.33)
. (1.33)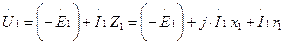 ;
;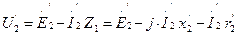 ; (1.34)
; (1.34)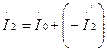 .
.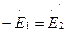 . В результате точки А и а, а также точки X и x: на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 33, б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.
. В результате точки А и а, а также точки X и x: на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 33, б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.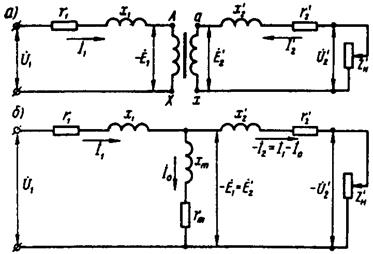
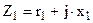 и током
и током 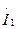 ; намагничивающей – сопротивлением
; намагничивающей – сопротивлением 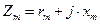 и током
и током 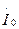 ; вторичной – с двумя сопротивлениями: сопротивлением собственно вторичной ветви
; вторичной – с двумя сопротивлениями: сопротивлением собственно вторичной ветви 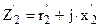 и сопротивлением нагрузки
и сопротивлением нагрузки 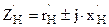 и током
и током 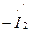 . Изменением сопротивления нагрузки
. Изменением сопротивления нагрузки 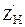 на схеме замещения могут быть воспроизведены все режимы работы трансформатора.
на схеме замещения могут быть воспроизведены все режимы работы трансформатора.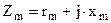 определяются током х.х. Наличие в этой ветви активной составляющей rm обусловлено магнитными потерями в трансформаторе.
определяются током х.х. Наличие в этой ветви активной составляющей rm обусловлено магнитными потерями в трансформаторе.










