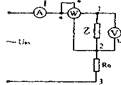
Вольт-амперные характеристики и параметры резистора, катушки индуктивности и конденсатора. Вах конденсатораВольт-амперные характеристики и параметры резистора, катушки индуктивности и конденсатора.Поиск ЛекцийЦель работы:Изучение трех основных элементов электрических цепей - резистора, катушки индуктивности и конденсатора; приобретение навыков снятия вольт-амперных характеристик и определения параметров элементов электрических цепей переменного тока. Снятие вольт-амперных характеристик. В данной лабораторнойработе резистор, катушка индуктивности (без ферромагнитногосердечника) иконденсатор исследуются только при синусоидальных напряжениях и токах. В этих условиях вольтамперная характеристика элемента электрической цепи есть зависимость между действующим значением напряжения, подаваемого на элемент, и действующим значением тока, потребляемого этим элементом. U = U(I) или I = I(U). Вольт-амперные характеристики снимаются по схеме, показанной на рис. 1.1. Схема собирается на универсальном лабораторном стенде, краткое описание которого дано в приложении.
Исследуемый элемент (либо резистор, либокатушка индуктивности, либо конденсатор),представленный на рисунке 1.1 комплекснымсопротивлением Z, подключается к клеммам 1 и 2.При сборке схемы в качестве точек 1 и 2 удобноиспользовать группы свободных контактов,имеющихся на стенде.
Рисунок 1.1. Схема Действующие значения напряжения U и тока измерительного стенда I, по которым строится вольтамперная характеристика, измеряются соответственно вольтметром V и амперметром А. На вход схемы от дискретно регулируемого источника подается синусоидальное входное напряжение По мере изменения действующего значения входного напряжения фиксируются соответствующие пары величин U и I, по которым строится вольт-амперная характеристика. В процессе проведения этого и последующих опытов, помимо всех обычных требований по технике безопасности, следует. 1. перед каждым переключением в схеме необходимо переводитьпереключатель источника в положение «0», 2. постепенно увеличивать входное напряжение, контролируяпоказания всех измерительных приборов (во избежание ихзашкаливания).
На сменной плате №1 стенда имеются три резистора (рис П9). В лабораторной работе исследуется только один резистор при трех положениях переключателя, изменяющего величину сопротивления R резистора Таким образом, снимаются три вольт-амперные характеристики, отвечающие трем значениям сопротивления R1 R2 и R3. Результаты измерений заносятся в таблицу 1.1. Таблица 1.1. Вольт-амперные характеристики резистора
В лабораторной работе исследуется только одна из трех катушек индуктивности, имеющихся на стенде. Снимаются три вольт-амперные характеристики, отвечающие трем положениям переключателя этой катушки. Результаты измерений заносятся в таблицу 1.2. Таблица 1.2 Вольт-амперные характеристики катушки индуктивности
Аналогичным образом снимаются три вольт-амперные характеристики одного из конденсаторов, отвечающие трем положениям его переключателя Результаты измерений заносятся в таблицу 1.3. Таблица 1.3. Вольт-амперные характеристики конденсатора
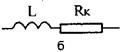
По результатам таблиц 1.1 -1.3 строятся вольт-амперные характеристики резистора, катушки индуктивности и конденсатора (по три характеристики для каждого элемента). Определение параметров исследуемых элементов. Основными электрическими параметрами исследуемых элементов являются: а) для резистора - сопротивление R; б) для катушки индуктивности - индуктивность L и сопротивлениеRk;
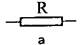
Рисунок 1.2. Принятые в лабораторной работе схемы замещения: а - резистор; б - катушка индуктивности; в - конденсатор. Электрические параметры электротехнических устройств определяются их конструктивными и физическими параметрами. Например, сопротивление резистора зависит от величины удельного сопротивления р, длины l и площади поперечного сечения S проводника, из которого изготовлен резистор;
Этой зависимостью можно воспользоваться и для определения сопротивления RK катушки индуктивности. Индуктивность L тороидальной катушки (а также длинной цилиндрической катушки) связана с ее физическими и конструктивными параметрами выражением
где ца - абсолютная магнитная проницаемость среды, в которой располагается магнитное поле катушки; со - число витков катушки; S -площадь поперечного сечения поля в катушке; l - длина средней силовой магнитной линии в катушке. Емкость С плоского конденсатора определяется абсолютной диэлектрической проницаемостью εа среды между обкладками конденсатора, площадью S обкладок и расстоянием h между обкладками:
Аналогичные формулы получены и для других конструктивных исполнений рассматриваемых элементов Однако воспользоваться этими формулами для практического определения искомых электрических параметров в большинстве случаев не удается. Экспериментальное определение многих величин, входящих в эти формулы, представляет собой достаточно трудную задачу, так как связано с необходимостью «заглянуть» внутрь элементов, что, как правило, приводит к их разрушению. Широкое применение получил косвенный метод определения электрических параметров элементов электрических цепей. Метод основан на применении закона Ома в символической форме:
где У и I - комплексы синусоидальных напряжений и тока исследуемого элемента; Z - комплексное сопротивление этого элемента, которое в общем случае (для любого элемента) имеет вид
где г - активное; х - реактивное сопротивление Из (1.2) следует взаимосвязь между действующими значениями напряжения U и тока I:
Согласно принятым схемам замещения исследуемых элементов (см. рис. 1.2) а) для резистора
где
поэтому из выражения (1.4) находим
I8 б) для катушки индуктивности
Где
и из выражения (1.4) получаем
в) для конденсатора
где
и согласно (1.4) имеем
Выражения (1.3) - (1.10) связывают величины действующих значении напряжения и и тока I, измеряемые на исследуемых элементах, с искомыми электрическими параметрами этих элементов В этом и состоит сущность используемого в данной лабораторной работе метода экспериментального определения параметров резистора катушки индуктивности и конденсатора, для которого достаточно измерений, сделанных в процессе снятия вольт-амперных характеристик. Подстановка величин U и I из таблицы 1.1 в формулу (1 3)позволяет вычислить полное сопротивление Z резистора (для каждогоположения переключателя). Так как при каждом положении переключателя было сделано несколько замеров величин U и I, то будет определено несколько значений величины Z (заносятся в таблицу 1.1), которые из-за погрешностей эксперимента могут незначительно отличаться друг от друга Эти значения величины Z усредняются и согласно равенству (1.5) дают искомые значения сопротивления R резистора, отвечающие соответствующим положениям переключателя. Итоговые (после усреднения) значения Z и R заносятся в таблицу 1.4. Аналогично определяется емкость конденсатора. Согласно формуле (1.3) по данным таблицы 1.3 находятся величины Z; они усредняются в соответствии с равенством (1.10) дают емкостное сопротивление хс конденсатора. Далее из выражения (1.9) вычисляется емкость С:
(при частоте входного напряжения f = 50 Гц угловая частота
Таблица 1.4
Расчет величин Z, Хс и С повторяется для трех положений переключателя. Результаты расчета заносятся в соответствующие графы таблицы 1.4. В отличие от резистора и конденсатора катушка индуктивности характеризуется двумя параметрами - индуктивностью L и сопротивлением RK. Поэтому определение параметров катушки оказывается более сложным. На основании формулы (1.3) вычисляются значения полного сопротивления Z катушки (исходные данные берутся из таблицы 1.2). Полученные значения усредняются (отдельно для каждого положения переключателя). Для определения сопротивления RK катушки используется взаимосвязь активной мощности Р с активным сопротивлением элемента и действующим значением тока I, протекающего по элементу.
Отсюда, учитывая, что в данном случае '" = ЛА , находим
Таким образом, измерив величины Р и I, можно найти искомое сопротивление RK (именно с этой целью в схему на рисунке 1.1 введен ваттметр W, а в таблице 1.2 предусмотрена графа «Р». Полученные по данным таблицы 1.2 значения RK усредняются. Далее на основании формулы (1.8) определяется индуктивное сопротивление xL катушки
и затем согласно выражению (1.7) находится искомая индуктивность L
Результаты расчета величин Z, RK, XL и L, вычисленные для трех положений переключателя, заносятся в соответствующие графы таблицы 1.4. В результате проведения всех расчетов полностью заполняется таблица 1.4. Найденные числовые значения параметров исследуемых элементов будут неоднократно использоваться при выполнении следующих лабораторных работ. Контрольные вопросы 1. Как изменяются электрические параметры исследованных элементов в зависимости от изменения действующего значения приложенного к нимнапряжения? 2. Как изменяются электрические параметры исследованных элементов в зависимости от изменения частоты приложенного к ним напряжения? 3. Резистор подключается: а) к источнику постоянного напряжения; б) к источнику переменного (синусоидального) напряжения Величина постоянного напряжения равна действующему значению переменного напряжения. В каком случае будет наблюдаться больший ток (по действующему значению)? 4 То же для катушки индуктивности. 5. То же для конденсатора. 6. Какие показания (и почему) давал ваттметр в опыте даннойлабораторной работы при исследовании конденсатора? 7. Оценить изменение величины сопротивления RK катушкииндуктивности в случае изменения (увеличения или уменьшения) в двараза: а) диаметра провода катушки; б) числа витков катушки; в) действующего значения приложенного напряжения; г) частоты приложенного напряжения. 8. В этих же случаях оценить изменение индуктивности L катушки. 9. В этих же случаях оценить изменение индуктивногосопротивления XL катушки. 10. В этих же случаях оценить изменение полного сопротивления Z катушки. 11. Оценить изменение емкостного сопротивления Хс конденсатора при изменении (увеличении или уменьшении) в два раза: а) действующего значения приложенного напряжения; б) частоты приложенного напряжения. 12. Как изменяется показания ваттметра в данной лабораторнойработе при исследовании катушки индуктивности в случае увеличения вдва раза: а) действующего значения приложенного напряжения? б) частоты приложенного напряжения? 13. Как по графикам вольт-амперных характеристик резистора,катушки индуктивности и конденсатора определить величиныэлектрических параметров этих элементов? Таблица 2.1
poisk-ru.ru 1.Краткие сведения о резисторах и конденсаторах.Резистор – пассивный элемент электрической цепи, в идеале характеризуемый активным сопротивлением. Основные параметры резистора: 1.Номинальное сопротивление. Номинальное сопротивление резисторов точностью до 10n,n Є D выбирают из так называемого номинального ряда. Е6,Е12,Е24,Е48,Е96,Е192. Цифра – количество значений в данном ряде. Каждый ряд соответствует определенному допуску в номиналах деталей. 1,0; 1,5; 2,2; 3,3; 4,7; 6,8. 2.Класс точности. 3.Номинальная мощность – это та максимальная рассеиваемая мощность, при которой параметры резистора существенно не меняются и он остается работоспособным длительное время. Обозначение мощности: Классификация резисторов:
2.По материалам (проволочные, полупроводниковые). Конденсатор - двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Основные параметры конденсатора: 1.Ёмкость. 2.Удельная ёмкость. 3.Номинальное напряжение. 4.Полярность. 5.Электрическое сопротивление изоляции. 6. Эквивалентное последовательное сопротивление. 7.Эквивалентная последовательная индуктивность. 8.Тангенс угла. 9.Температурный коэффициент ёмкости. 10.Диэлектрическое поглощение. Классификация:
2. Собственная и примесная проводимость полупроводников. Электронно-дырочный n-p переход. Вольт-амперная характеристика.Полупроводники — это вещества, удельное сопротивление которых убывает с повышением температуры, наличием примесей, изменением освещенности. В идеальном кристалле ток создается равным количеством электронов и «дырок». Такой тип проводимости называют собственной проводимостью полупроводников. При повышении температуры (или освещенности) собственная проводимость проводников увеличивается. На проводимость полупроводников большое влияние оказывают примеси. Примеси бывают донорные и акцепторные. Донорная примесь — это примесь с большей валентностью. При добавлении донорной примеси в полупроводнике образуются лишние электроны. Проводимость станет электронной, а полупроводник называют полупроводником n-типа. Акцепторная примесь — это примесь с меньшей валентностью. При добавлении такой примеси в полупроводнике образуется лишнее количество «дырок». Проводимость будет «дырочной», а полупроводник называют полупроводником р-типа. Принцип действия большинства полупроводниковых приборов основан на свойствах р—n-перехода. При приведении в контакт двух полупроводниковых приборов р-типа и л-типа в месте контакта начинается диффузия электронов из n-области в р-область, а «дырок» — наоборот, из р- в n-область. Этот процесс будет не бесконечным во времени, так как образуется запирающий слой, который будет препятствовать дальнейшей диффузии электронов и «дырок». Вольт-амперная характеристика (ВАХ) — график зависимости тока через двухполюсник от напряжения на этом двухполюснике. Вольт-амперная характеристика описывает поведение двухполюсника на постоянном токе. studfiles.net Конденсатор (электрический) - это... Что такое Конденсатор (электрический)?Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик Слева - конденсаторы для поверхностного монтажа; справа - конденсаторы для объёмного монтажа; сверху - керамические; снизу - электролитические. Различные конденсаторы для объёмного монтажа Конденса́тор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. ИсторияВ 1745 году в Лейдене немецкий физик Эвальд Юрген фон Клейст и голландский физик Питер ван Мушенбрук создали первый конденсатор — «лейденскую банку». Свойства конденсатораКонденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течет, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора. В терминах метода комплексных амплитуд конденсатор обладает комплексным импедансом , где — мнимая единица, — частота[1] протекающего синусоидального тока, — ёмкость конденсатора. Отсюда также следует, что реактивное сопротивление конденсатора равно: . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае). При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью , собственной индуктивностью и сопротивлением потерь . Резонансная частота конденсатора равна При конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной. Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора: где — напряжение (разность потенциалов), до которого заряжен конденсатор. Обозначение конденсаторов на схемахВ России условные графические обозначения конденсаторов на схемах должны соответствовать ГОСТ 2.728-74[2] либо международному стандарту IEEE 315-1975:
На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 106 пФ) и пикофарадах, но нередко и в нанофарадах. При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, т.е. постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения (пикоФарад). Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мк x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 – 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, т.е. на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду. Характеристики конденсаторовОсновные параметрыЁмкостьОсновной характеристикой конденсатора является его ёмкость. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до сотен микрофарад. Однако существуют конденсаторы с ёмкостью до десятков фарад. Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью каждая, расположенных на расстоянии друг от друга, в системе СИ выражается формулой: , где — относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (эта формула справедлива, лишь когда много меньше линейных размеров пластин). Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею. или Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади. При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы. Общая ёмкость батареи последовательно соединённых конденсаторов равна или Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения. Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов. Удельная ёмкостьКонденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя. Номинальное напряжениеДругой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах. Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается. ПолярностьКонденсаторы, разрушившиеся без взрыва из-за температуры и напряжения, не соответствующих рабочим. Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса. Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения (актуально для импульсных устройств). Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают клапан или выполняют насечку на корпусе (часто можно заметить её в форме буквы X, K или Т на торце). При повышении внутреннего давления открывается клапан или корпус разрушается по насечке, испарившийся электролит выходит в виде едкого газа, и давление спадает без взрыва и осколков. Паразитные параметрыРеальные конденсаторы, помимо ёмкости, обладают также собственными сопротивлением и индуктивностью. С высокой степенью точности, эквивалентную схему реального конденсатора можно представить следующим образом: Электрическое сопротивление изоляции конденсатора — rСопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением r = U / Iут , где U — напряжение, приложенное к конденсатору, Iут — ток утечки. Эквивалентное последовательное сопротивление — RЭквивалентное последовательное сопротивление (ЭПС, англ. ESR) обусловлено главным образом электрическим сопротивлением материала обкладок и выводов конденсатора и контакта(-ов) между ними, а также потерями в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор. В большинстве случаев этим параметром можно пренебречь, но иногда (напр., в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания) достаточно малое его значение может быть жизненно важным для надёжности устройства (см., напр., Capacitor plague(англ.)). Эквивалентная последовательная индуктивность — LЭквивалентная последовательная индуктивность обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. На низких частотах (до единиц килогерц) обычно не учитывается в силу своей незначительности. Тангенс угла потерьТангенс угла потерь - отношение мнимой и вещественной части комплексной диэлектрической проницаемости. Потери энергии в конденсаторе определяются потерями в диэлектрике и обкладках. При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол , где — угол диэлектрических потерь. При отсутствии потерь . Тангенс угла потерь определяется отношением активной мощности Pа к реактивной Pр при синусоидальном напряжении определённой частоты. Величина, обратная , называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов. Температурный коэффициент ёмкости (ТКЕ)ТКЕ — относительное изменению емкости при изменении температуры окружающей среды на один градус Цельсия (Кельвина). Таким образом значение ёмкости от температуры представляется линейной формулой: ,где ΔT - увеличение температуры в °C или °К относительно нормальных условий, при которых специфицировано значение ёмкости. TKE применяется для характеристики конденсаторов со значительной линейной зависимостью ёмкости от температуры. Однако ТКЕ определяется не для всех типов конденсаторов. Конденсаторы, имеющие нелинейную зависимость емкости от температуры, и конденсаторы с большими уходами емкости от воздействия температуры окружающей среды в обозначении имеют указание на относительное изменение емкости в рабочем диапазоне температур. Диэлектрическое поглощениеЕсли заряженный конденсатор быстро разрядить до нулевого напряжения путём подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то мы увидим, что напряжение медленно повышается. Это явление получило название диэлектрическое поглощение или адсорбция электрического заряда. Конденсатор ведёт себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора. Подобный эффект можно наблюдать и на большинстве электролитических конденсаторов, но в них он является следствием химических реакций между электролитом и обкладками. Наименьшим диэлектрическим поглощением обладают конденсаторы с органическими диэлектриками: тефлон (фторопласт), полистирол, полиэтилентерефталат, поликарбонат. Классификация конденсаторовОсновная классификация конденсаторов проводится по типу диэлектрика в конденсаторе. Тип диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность ёмкости, величину потерь и др. По виду диэлектрика различают:
Кроме того, конденсаторы различаются по возможности изменения своей ёмкости:
В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляюшие, дозиметрические, пусковые и другие конденсаторы. Применение конденсаторовКонденсаторы находят применение практически во всех областях электротехники.
Внешние ссылкиСмотри такжеСсылки
dic.academic.ru Конденсатор: формулы для конденсаторовСодержание:
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком. В чем измеряется емкость конденсатораОдной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства. Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества. Для расчетов емкости плоского конденсатора используется формула: в которой ε0 = 8,854187817 х 10-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками. Формула энергии конденсатораС емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу. В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой. Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения. Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU2/2. Формула заряда конденсатораДля выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E. Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc. В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар). Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора. Формула тока утечки конденсатораТок утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности. Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока. Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции. electric-220.ru Исследование цепи, состоящей из последовательно соединенных катушки со стальным сердечником и конденсатора, изучение триггерного эффекта, страница 2Затем производится снятие ВАХ последовательно соединенных нелинейной индуктивности и линейной емкости. Для этого посредством автотрансформатора ступенчато увеличивают напряжение на входе схемы, начиная с 0. По амперметру фиксируется скачкообразное увеличение тока. Записываются показания приборов непосредственно до и после скачка тока. Потом напряжение на входе начинают плавно уменьшать вплоть до скачкообразного уменьшения тока. Также записываются показания приборов до и после скачка тока. Измерения повторяются для другого значения емкости линейного конденсатора. РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ Во время выполнения работы нами производились измерения искомых величин: зависимость напряжения на дросселе от тока, зависимость напряжения на конденсаторе от тока и зависимость напряжения на последовательно соединенных дросселе и конденсаторе от тока. Измерения проводились следующим образом: при помощи автотрансформатора плавно изменялось входное напряжение, затем снимались показания приборов (вольтметра и амперметра). Результаты измерений приведены в соответствующих таблицах: «ВАХ дросселя», «ВАХ конденсатора» и «ВАХ феррорезонанса». ВАХ дросселя:
ВАХ конденсатора:
ВАХ феррорезонанса:
В ходе работы нам предлагалось снять ВАХ катушки со стальным сердечником (дросселя) и линейного конденсатора в диапазоне напряжений 0 – 300 В и токов – 0 – 5 А, плавно изменяя напряжение, а также измерить ВАХ последовательно соединенных дросселя и конденсатора. Результаты измерений приведены в пункте «РЕЗУЛЬТАТЫ ИЗМЕРЕНИЙ». По полученным данным требовалось построить графики зависимости напряжения на катушке, конденсаторе и последовательно соединенных катушке и конденсаторе от тока. Также было необходимо построить теоретическую кривую зависимости напряжения на последовательно соединенных конденсаторе и катушке от тока, пользуясь измеренными ВАХ для катушки и конденсатора в отдельности (считая, что потери в сердечнике дросселя и активное сопротивление равны нулю). Для этого требовалось произвести вычитание значений напряжения на конденсаторе из значений напряжения на нелинейной индуктивности при одном и том же значении тока; взять модуль полученного значения и отложить его на графике. Все графики построить в одной системе координат. Результаты вычислений приведены в таблице:
Пользуясь этими данными, нами были построены графики искомых величин (см. диаграмму в начале пункта). Теоретическая кривая выполнена пунктирной линией. Также необходимо построить векторные диаграммы до и после скачка тока. На них видно, что ток до скачка отставал от напряжения на 90o, а после скачка стал опережать его на 90o, таким образом сдвиг фазы тока составил 180o.
ВЫВОДВ ходе выполнения данной лабораторной работы нами была исследована нелинейная электрическая цепь, состоящая из последовательно соединенных катушки со стальным сердечником и линейного конденсатора, на вход которой подавалось переменное напряжение с промышленной частотой 50 Гц, плавно изменяемое при помощи лабораторного автотрансформатора. Согласно теории, данная цепь имеет N-образную вольт-амперную характеристику, вследствие чего в ней возникает явление, называемое феррорезонансом напряжений. Основное следствие этого явления – триггерный эффект, или скачкообразное изменение тока в цепи при незначительном изменении напряжения на ее входе. На опыте мы наблюдали триггерный эффект в исследуемой цепи и определили токи и напряжения до и после скачка тока как при возрастании напряжения, так и при его убывании. Также нами были измерены ВАХ нелинейной индуктивности и линейной емкости. На основании полученных данных мы построили экспериментальную и теоретическую кривые U = f(I) и сопоставили их. Мы выяснили, что увеличение емкости конденсатора вызывает увеличение напряжений, при которых наблюдается триггерный эффект, и увеличение скачков тока. Также мы выяснили, что фаза тока при достижении феррорезонанса сдвигается на 180o (опрокидывание фазы). На опыте мы убедились в существовании триггерного эффекта в нелинейной электрической цепи, образованной последовательно соединенными индуктивностью и емкостью, и измерили его основные параметры. На основании этого можно сделать вывод, что цель работы нами была достигнута полностью. vunivere.ru 2.3. Основные характеристики конденсаторов | ЭлектротехникаОсновной характеристикой конденсатора является его электрическая емкость (С), определяемая отношением накапливаемого на обкладках электрического заряда (Q) к приложенному к обкладкам напряжению (U): С = k где k – постоянный коэффициент, S – площадь обкладок, n – число обкладок, d – расстояние между обкладками, e – диэлектрическая проницаемость. Если конденсатор выполнен на основе комбинированной изоляции, то диэлектрическая проницаемость может быть дополнительно определяемой в зависимости от состава ингредиентов. В частности, для комбинированной бумажно-пленочной изоляции диэлектрическая проницаемость может быть определена по формуле: e= где e1 – диэлектрическая проницаемость материала, используемого в качестве пленки толщиной d1; e2 – диэлектрическая проницаемость конденсаторной бумаги с толщиной слоя d2. Конденсаторы постоянной емкости характеризуются номинальным значением емкости; конденсаторы переменной емкости характеризуются диапазоном емкостей Сmin – Сmax. Сопротивление изоляции конденсатора (Rиз) определяется свойствами диэлектрика и конструкционными особенностями конденсатора. Это сопротивление зависит от температуры и влажности окружающей среды и лежит в пределах от 1 · 109 Ом для сегнетокерамических конденсаторов до 1 · 1012 Ом для пленочных конденсаторов. Сопротивление комбинированной бумажно-пленочной изоляции определяется по формуле: R = Добротность (Q) конденсатора определяется потерями энергии в диэлектрике и металлических обкладках и выражается отношением: Q = PR/PA, (2.2) где PR – реактивная мощность; PA – полные потери энергии в конденсаторе. Так как полные потери энергии в конденсаторе в единицу времени (активная мощность) определяются суммой потерь энергии в диэлектрике конденсатора (Pд) и потерь энергии в металлических обкладках (Pм), то добротность конденсатора определяется выражением: Q = PR /( Pд + Pм ). (2.3) Добротность различных типов конденсаторов изменяется от нескольких процентов до 10 раз. Потери конденсатора часто характеризуют тангенсом угла потерь (tg dC): tg dC = 1/Q, (2.4) и определяются, главным образом, потерями в диэлектрике, величина которых зависит от влажности и температуры. В современных конденсаторах наибольшее влияние на потери оказывает температура. Потери в комбинированном бумажно-пленочном диэлектрике определяются соотношением ингредиентов: tg где Реактивная мощность конденсаторов, предназначенных для работы в цепях переменного тока, может быть представлена в виде: PR = UI sinj. (2.5) Потери большинства конденсаторов незначительны, и сдвиг фаз между током и напряжением близок к 90о. Поэтому справедливо выражение: PR = UI, где U – эффективное значение напряжения на конденсаторе, I – ток, проходящий через конденсатор. Так как I = UwC, то PR = U2 wC. Стандартные низковольтные конденсаторы имеют реактивную мощность от 25 до 75 вар. Электрическая прочность конденсатора характеризует зависимость напряжения, приложенного к его зажимам, от времени, в течение которого не произойдет пробоя. Время работы, на которое рассчитывается конденсатор, обычно исчисляется де electrono.ru Электрический конденсатор
Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик
Слева — конденсаторы для поверхностного монтажа; справа — конденсаторы для объёмного монтажа; сверху — керамические; снизу — электролитические. На полярных SMD конденсаторах + обозначен полоской.
Различные конденсаторы для объёмного монтажа
История: В 1745 году в Лейдене немецкий физик Эвальд Юрген фон Клейст и голландский физик Питер ван Мушенбрук создали первый конденсатор — «лейденскую банку». Свойства конденсатора Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения. С точки зрения метода комплексных амплитудконденсатор обладает комплекснымимпедансом , где —мнимая единица,—частота[1]протекающегосинусоидальноготока,— ёмкость конденсатора. Отсюда также следует, чтореактивное сопротивлениеконденсатора равно:. Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае). При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивностии сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательныйколебательный контур, образуемый ёмкостью, собственной индуктивностьюи сопротивлением потерь. Резонансная частотаконденсатора равна
При конденсатор в цепи переменного тока ведёт себя каккатушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах, на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной. Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
где —напряжение(разность потенциалов), до которого заряжен конденсатор. Обозначение конденсаторов на схемахВ России условные графические обозначения конденсаторов на схемах должны соответствовать ГОСТ2.728-74[2]либо международному стандартуIEEE315—1975:
На электрических принципиальных схемахноминальная ёмкость конденсаторов обычно указывается вмикрофарадах(1 мкФ = 106пФ) и пикофарадах, но нередко и в нанофарадах. При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения. Дляэлектролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мк x 10 В». Дляпеременных конденсаторовуказывают диапазон изменения ёмкости, например так: «10 — 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями издесятичнологарифмических рядов значений Е3, Е6, Е12, Е24, то есть на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду. studfiles.net |
|
||||||||||||||||||
|
|
||||||||||||||||||
|




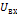 . Диапазон регулирования действующего значения входного напряжения указан на источнике.
. Диапазон регулирования действующего значения входного напряжения указан на источнике.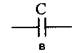
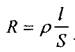
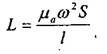 (1.1)
(1.1)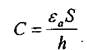
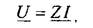 (1.2)
(1.2)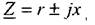 (1.3)
(1.3)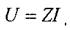 (1.3) где Z - полное сопротивление, записываемое в виде
(1.3) где Z - полное сопротивление, записываемое в виде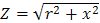 (1.4)
(1.4)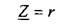
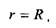
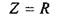 (1.5)
(1.5)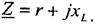
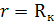 (1.6)
(1.6)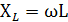 (1.7)
(1.7)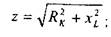 (1.8)
(1.8)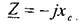
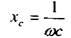 (1.9)
(1.9)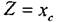 (1.10)
(1.10)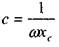
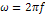 = 314 рад/с).
= 314 рад/с).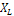 , Ом
, Ом
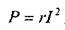
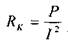
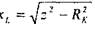
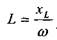
 ЛАБОРАТОРНАЯ РАБОТА №2
ЛАБОРАТОРНАЯ РАБОТА №2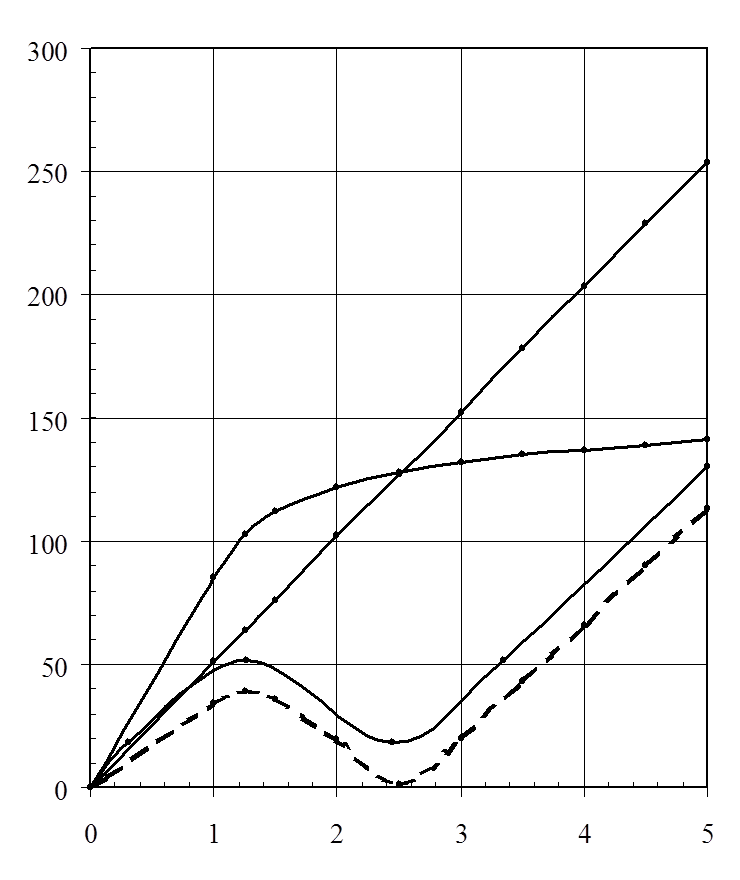
 e, (2.1)
e, (2.1) ,
, .
. ,
, – тангенс угла диэлектрических потерь материала, используемого в качестве пленки толщиной d1 и диэлектрической проницаемостью e1;
– тангенс угла диэлектрических потерь материала, используемого в качестве пленки толщиной d1 и диэлектрической проницаемостью e1;  – тангенс угла диэлектрических потерь конденсаторной бумаги с толщиной слоя d2 и диэлектрической проницаемостью e2.
– тангенс угла диэлектрических потерь конденсаторной бумаги с толщиной слоя d2 и диэлектрической проницаемостью e2.