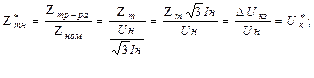Внезапное трехфазное короткое замыкание синхронного генератора. Трехфазное короткое замыканиеВнезапное трехфазное короткое замыкание синхронного генератораПри исследовании статических режимов синхронной машины мы использовали уравнение напряжений
полученное из физических представлений на основе понятия о вращающихся магнитных полях. Такой подход позволил сравнительно просто выявить основные свойства и характеристики синхронных машин в установившихся режимах. Поведение же синхронной машины в динамических режимах описывается системой дифференциальных уравнений. Однако для качественного анализа электромагнитных переходных процессов также удобно использовать физический подход. Рассмотрим внезапное симметричное короткое замыкание синхронного генератора из режима холостого хода при Расчет токов короткого замыкания трехфазного явнополюсного генератора с обмоткой возбуждения f и двумя короткозамкнутыми эквивалентными демпферными обмотками
Однако строгое аналитическое решение данной системы уравнений оказывается достаточно сложным. С целью упрощения воспользуемся теоремой о постоянстве потокосцепления короткозамкнутого сверхпроводящего контура. Поскольку в сверхпроводящем контуре активное сопротивление
и, следовательно, потокосцепление
Реальные контуры синхронных машин обладают малым активным сопротивлением, и для начального периода короткого замыкания можно принять активные сопротивления всех обмоток равными нулю. Пусть в первый момент короткого замыкания (
где Согласно теореме о постоянстве потокосцепления полные потокосцепления фаз Возникновение двух магнитных полей реакции якоря вызывает, в соответствии с теоремой о постоянстве потокосцеплений замкнутых роторных контуров, токи, противодействующие образованию новых магнитных полей и тем самым обеспечивающие постоянство потокосцеплений соответствующих обмоток. Внезапное возникновение вращающегося магнитного поля реакции якоря Трансформаторная связь между апериодическими токами ротора и периодическими токами статора может быть выражена уравнениями потокосцеплений. В соответствии с теоремой о постоянстве потокосцеплений каждой обмотки по оси d имеем
где
Первое уравнение определяет потокосцепление фазы «а» при
Этим уравнениям соответствует схема замещения (рис.5.59). Входное сопротивление схемы
называется сверхпереходным индуктивным сопротивлением обмотки статора по оси d. Величина сопротивления
Так как сопротивления роторных обмоток
называется переходным индуктивным сопротивлением обмотки статора по оси d. В сравнении с
В дальнейшем по мере затухания апериодического тока
представляет собой полное индуктивное сопротивление машины по продольной оси в установившемся режиме. Решая первое уравнение потокосцеплений, находим периодическую составляющую тока якоря
или
Первый член этого уравнения соответствует установившемуся току короткого замыкания, индуцируемому в обмотке якоря током возбуждения
а после затухания апериодического тока демпферной обмотки (рис. 5.61) ток
Данные соотношения позволяют определить токи
Апериодические токи обмотки возбуждения и демпферной обмотки затухают с постоянными времени
Она называется постоянной времени переходного процесса. Постоянная времени сверхпереходного процесса
Таким образом, периодическая составляющая тока якоря
Отсюда получаем мгновенное значение периодического тока короткого замыкания в фазе «а»:
Рассмотрим закон изменения апериодической составляющей тока статора Поэтому схема замещения синхронной машины по оси q будет иметь вид, представленный на рис. 5.66. Входное сопротивление схемы
называется сверхпереходным индуктивным сопротивлением синхронной машины по поперечной оси. В первый момент короткого замыкания при
Так как этот ток является свободным и не поддерживается внешними источниками, то он с течением времени затухает до нуля,
где Реакция ротора на постоянный магнитный поток (рис. 5.59 и 5.65) аналогична реакции на поток обратной последовательности, поэтому постоянная При магнитной или электрической несимметрии ротора апериодическая составляющая
Для произвольного положения ротора в первый момент короткого замыкания апериодическая составляющая тока фазы «а» статора определится из выражения
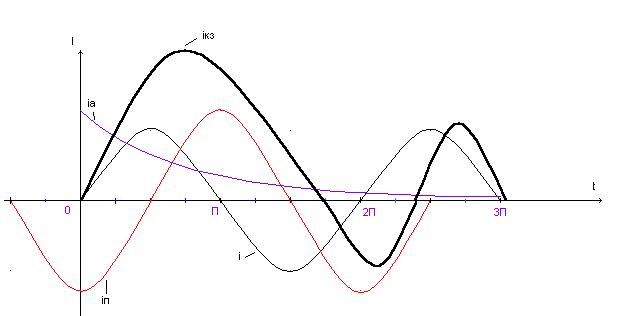
Характер изменения во времени составляющих
Наибольший ток короткого замыкания называется ударным током короткого замыкания
Ток короткого замыкания создает весьма опасные электродинамические усилия в зоне лобовых частей обмотки статора. Эти усилия стремятся отогнуть лобовые части обмотки статора к торцевой поверхности сердечника статора. ГОСТ ограничивает величину ударного тока короткого замыкания мощных машин значением Переходные токи короткого замыкания создают также знакопеременный момент на валу машины. Амплитуда этого момента может в 5¸15 раз превышать номинальный момент, поэтому его необходимо учитывать при расчете на прочность валов и муфт, соединяющих синхронный генератор с турбиной. Тепловые воздействия токов короткого замыкания не представляют большой опасности для генератора, так как длительность короткого замыкания обычно не превышает 1 с.
Похожие статьи:poznayka.org Тема 3. Трехфазное короткое замыкание в электрической сети1. Чем характеризуются «шины бесконечной мощности»? 2. Какими параметрами определяется постоянная времени и какова её физическая сущность? 3. Для каких условий возникновения короткого замыкания рассчитывается ударный ток? Тема 4. Параметры и режимы электрических машин...............1. Какое влияние оказывают демпферные обмотки на протекание переходного процесса? 2. Какие параметры определяют синхронную машину в установившемся режиме? 3. В чем суть принципа Ленца применительно к магнитным цепям? 4. Какими параметрами характеризуются синхронные машины в начальный момент внезапного нарушения режима? Обоснуйте их физическую подоплеку и условия расчета. 5. Чем обусловлена необходимость гашения магнитного поля системы возбуждения синхронных машин? 6. Что понимается под форсировкой возбуждения и какие факторы определяют её эффективность? 7. Назовите постоянные времени, которые определяют переходный процесс синхронного генератора при наличии и отсутствии демпферных обмоток? 8. На какие слагаемые тока переходного режима оказывает влияние АРВ? 9. В чём проявляется влияние двигательной нагрузки на токи переходного режима? Тема 5. Практические методы расчета токов трехфазного кз1. Что понимается под коэффициентами токораспределения и какова суть их практического приложения? 2. В каких случаях возникает необходимость обращаться к типовым кривым для расчета периодической слагаемой тока КЗ? 3. Каким параметром характеризуется условная электрическая удаленность источников питания от места короткого замыкания? 4. Какими параметрами учитываются генераторы, синхронные и асинхронные двигатели при расчете режима КЗ? 5. При каких условиях рекомендуется учитывать двигательную нагрузку при расчёте режима КЗ? Тема 6. Параметры элементов для токов обратной и нулевой последовательностей1. В чем достоинства и недостатки метода симметричных составляющих при его применении к расчетам несимметричных режимов в электрических системах? 2. Каковы особенности расчета сопротивлений обратной и нулевой последовательностей для силовых элементов энергосистемы? 3. От каких факторов зависит схема замещения и реактивное сопротивление нулевой последовательности () трансформаторов? 4. Для каких трансформаторов с соединением в схеме нулевой последовательности при расчетенеобходимо учитыватькак конечную величину? 5. Почему в схеме нулевой последовательности трансформатора с соединением обмоток за обмоткойимеет место нулевой потенциал? 6. Чем обусловлено различие ивоздушных линий? 7. В чем проявляется влияние заземленных тросов воздушных линий электропередач на ? 8. При каких условиях справедлив принцип независимости действия симметричных составляющих; в чем его сущность и практическая применимость? 9. В чем отличие схем замещения обратной и нулевой последовательностей от прямой последовательности? 10. Что является источником токов обратной и нулевой последова-тельностей? 11. Какие узлы являются началом и концом схем замещения различных последовательностей при поперечной несимметрии? 12. В чём особенность учёта сопротивления в нейтрали трансформатора в схеме нулевой последовательности? studfiles.net Трехфазное короткое замыкание в простейшей неразветвленной цепи.Составляющие тока короткого замыкания.Простейшей трехфазной цепью будем считать цепь без трансформаторных связей. Принимаем, что источник питания обладает бесконечной мощностью. На одной (левом) участке взаимоиндукция между фазами, на другом она отсутствует. Цепь присоединена к источнику синусоидального напряжения с неизменной амплитудой и частотой.
Рис. 1. Простейшая трехфазная электрическая цепь.
Переходный процесс вызывается включением выключателя В, на котором сделана закоротка, т.е. возникает металлическое трехфазное короткое замыкание между двумя участками цепи.
Рис.2. Векторная диаграмма для начального момента трехфазного короткого замыкания.
Пусть векторы
Решение этого уравнения имеет вид:
Где Это решение показывает, что здесь имеется лишь свободный ток, который затухает по экспоненте с указанной постоянной времени.
Нет источника питания.
Начальное значение свободного тока в каждой фазе зашунтированного участка цепи, очевидно, равно предшествующему мгновенному значению тока (первый закон коммутации iL(0_)= iL(0+)), поскольку в цепи с индуктивностью не может произойти внезапного изменения (скачка) тока. В общем случае свободные токи в фазах различны, хотя их затухания происходят с одной и той же постоянной времени. В одной из фаз свободный ток может вообще отсутствовать, если в момент возникновения короткого замыкания предшествующий ток в этой фазе проходит через нуль; при этом свободные токи в двух других фазах будут одинаковы по величине, но противоположны по направлению.
Перейдем теперь к участку цепи, который остался присоединенным к источнику. (Левая часть схемы). Здесь помимо свободного тока будет новый принудительный ток, величина которого больше предыдущего и сдвиг и сдвиг по фазе в общем случае иной. IПА, IПВ, IПС, φк. Запишем дифференциальное уравнение равновесия для любой из фаз этого участка, например, фазы А. С учетом взаимной индуктивности контуров – коэффициент М – уравнение будет иметь вид:
Известно, что для трехпроводной системы:
Если обозначить результирующую индуктивность фазы с учетом влияния двух других фаз
Т.е. имеем линейное дифференциальное уравнение, а общий интеграл линейного дифференциального уравнения равен сумме частного решения неоднородного уравнения плюс полное решение однородного уравнения. Однородное уравнение получаем из исходного (4), если в нем левую часть взять равной нулю:
Частное решение неоднородного уравнения равно Поэтому решение линейного дифференциального уравнения можно записать в виде:
где zk – полное сопротивление присоединенного к источнику участка цепи, т.е. сопротивление цепи короткого замыкания; φk – угол сдвига в этой цепи в режиме короткого замыкания;
Первый член (слагаемое) правой части уравнения (или частное решение неоднородного дифференциального уравнения) называется принужденной составляющей тока и представляет периодическую слагаемую тока с постоянной амплитудой
где i0 – полный ток, т.е. t=0. Подставляя в это выражение начальное значение полного тока i0 и его периодической составляющей
φ – начальный угол. Знак «-», т.к. ток отстает от напряжения на угол φ; φк – т.к. появляется апериодическая составляющая после короткого замыкания. Знак «-», т.к. ток отстает от напряжения. На векторной диаграмме принудительные токи будут выглядеть следующим образом. Поскольку токи iп и i0 являются проекциями векторов Для практических целей важно определить максимальное возможное мгновенное значение тока короткого замыкания. Из предыдущего уравнения (8) следует, что наибольшее значение апериодической составляющей тока определяется не только фазой включения α, но также предшествующим режимом цепи. Так, например, при отсутствии предшествующего тока Im=0 в цепи величина При отсутствии предшествующего тока (Im=0) следует, что полный ток в цепи короткого замыкания является функцией двух независимых переменных: времени t и фазы включения α и выражается уравнением: в (8) в (6)
Приравниваем к нулю частные производные этого уравнения, т.е.:
Совместное решение этих уравнений показывает, что максимум тока наступает при :
т.е. при α=0 (т.е. согласно рис.2 UA проходит через 0). Следовательно, в предварительно разомкнутой цепи с r и L максимум мгновенного значения полного тока при коротком замыкании наступает, если в момент возникновения короткого замыкания напряжение источника проходит через нуль. Для цепи с преобладающей индуктивностью φк≈900, поэтому условие возникновения максимума апериодической слагающей и условие, при котором достигается максимум мгновенного значения полного тока, очень близки друг к другу.
Дата добавления: 2014-12-09; просмотров: 1. Поделиться с ДРУЗЬЯМИ:refac.ru Тема 5.1. Трехфазные короткие замыкания⇐ ПредыдущаяСтр 9 из 14Следующая ⇒Короткое замыкание-это электрическое соединение токоведущих частей проводников, приводящее к снижению сопротивления электрической цепи, возрастанию тока и снижению напряжения. Причины КЗ: Механическое разрушение изоляции, перегрев и пробой изоляции, падение опоры воздушной линии, схлестывание проводов. Различают следующие виды КЗ. Трехфазное симметричное КЗ Двухфазное КЗ на землю
Основные понятия и соотношения iуд – Максимальный ударный ток. Ia – Апериодическая составляющая. Iп – Периодическая составляющая. С момента возникновения КЗ, в системе электроснабжения, переходный процесс, который характеризуется изменением двух составляющих тока КЗ: периодической и апериодической. Для выбора аппаратов и проводников, а также проверки их по условиям КЗ, подсчитывают: Iпо- это наибольшее начальное действующее значение периодической составляющей тока КЗ; Int- действующее значение периодической составляющей тока КЗ; iао- начальное значение апериодической составляющей; iat – значение апериодической составляющей тока КЗ в начальный момент времени; iy- ударный ток - максимальное удельное значение тока КЗ.
В расчетах интересуются максимально возможным ударным током. Это имеет место, если цель работы в режиме холостого хода до короткого замыкания. При этом начальное значение апериодической составляющей равно максимальному периоду
Назначение и порядок расчета токов КЗ. Ток КЗ рассчитывается для: 1. Проверки выбранного электрооборудования на динамическую и термическую устойчивость (рассчитывается максимальный ток КЗ) 2. Для проверки и выбора уставок релейной защиты рассчитывается максимальный ток КЗ. Максимальный ток КЗ для одной фазы трехфазной цепи, для которого периодическая составляющая тока максимальна. Минимальный ток КЗ – это чаще всего ток двухфазного КЗ. Для упрощенных расчетов тока КЗ принимают допущения. 1. ЭДС всех генераторов питающих точку КЗ совпадают по фазе в течение всего КЗ. 2. Не учитывается насыщение магнитопровода генератора и трансформатрора, т.е. индуктивное сопротивление постоянно. 3. Емкостные проводимости линий не учитываются, кроме случая однофазных КЗ в сети с изолированной нейтралью. 4. Если индуктивное сопротивление в 3 5. Преобразование схемы замещения к виду, где каждый характерный источник ЭДС (может быть замещающий группу источников) связан с точкой КЗ одним эквивалентным сопротивлением Zраз или Xраз. 6. Имея результирующие ЭДС и эквивалентные сопротивления, определяют начальное значение периодической составляющей тока КЗ, Iy и, если нужно, Int и iat для момента времени t. Расчетная схема установки это упрощенная линейная схема указанием всех параметров, которые влияют на точку КЗ.
При расчетах тока КЗ в сетях выше 1000 В, учитывается только индуктивное сопротивление. При расчетах в сетях ниже 1000 В, дополнительно учитывается активное сопротивление всех элементов и сопротивление шин первичных обмоток трансформаторов тока в контактах и катушках в индуктивных аппаратах. Напряжение в точках сети в нормальном и тем более в аварийных режимах разные. При расчетах тиристоров, для каждой ступени применяют одно напряжение равное среднему напряжению сети.
Сопротивление элементов сети на расчетной схеме указываются в относительных единицах, т.е. в долях от базовой системы величин, например от минимальных.
Эти параметры могут быть выражены также в долях базовых величин, взятых за основу всего расчета. Читайте также: lektsia.com Симметричное трехфазное короткое замыкание — КиберПедияСоставление расчетной схемы системы электроснабжения На рисунке 1 представлена схема системы электроснабжения, на основании ее составим расчетную схему (рис 1.1).
Рисунок 1.1 – Расчетная схема системы электроснабжения
Симметричное трехфазное короткое замыкание Расчет установившегося режима При определении переходного тока ЭДС обобщенной нагрузки , переходное сопротивление генератора , а Обобщенная нагрузка в сверхпереходном режиме принимается равной 1,2. Остальные величины остаются не изменными. ЭДС генератора рассчитывается по формуле: , (2.28) где - приведенное напряжение на выводах генератора в момент, предшествующий КЗ; - приведенный ток статора в момент, предшествующий КЗ; - угол сдвига фаз напряжения и тока в момент, предшествующий КЗ, рад. Сопротивление генератора рассчитывается по формуле: , (2.29) где - сопротивление генератора в относительных единицах при номинальных условиях; – номинальная мощность генератора, . Последующий расчет и преобразование схемы аналогично п. 2.1 . Преобразуем треугольник сопротивлений в эквивалентную звезду: Установившийся ток в относительных единицах: Установившийся ток в именованных единицах:
Несимметричный режим Расчет токов несимметричных коротких замыканий проводят с использованием метода симметричных составляющих.Любую не симметричную систему можно разложить на три симметричных составляющих прямой, обратной и нулевой последовательности фаз. Расчет обратной последовательности фаз Составим схему замещения обратной последовательности фаз (рис. 3.5). Рисунок 3.5 – Схема замещения обратной последовательности фаз системы электроснабжения При обратной последовательности фаз учитываются все элементы исходной расчетной схемы (рис. 2), а их сопротивления такие же, как и при сверхпереходном режиме, а ЭДС равны 0. Т.к. сопротивления элементов такие же как в п. 3.1, то эквивалентное сопротивление схемы замещения . Напряжения прямой, обратной и нулевой последовательностей Напряжения прямой, обратной и нулевой последовательностей особой фазы в месте КЗ определяются по формулам: ; (3.28) ; (3.29) ; (3.30) Построим векторную диаграмму напряжений (рис. 3.10), по полученным значениям токов в п. 3.5. Рисунок 3.10 – Векторная диаграмма напряжений Где фаза А обозначена желтым цветом, фаза В зеленым, фаза С красным. Список использованных источников 1. Методические указания к выполнению контрольной работы по дисциплине «Электромагнитные переходные процессы в электроэнергетических системах» / сост. В. А. Агеев, Ю. И. Шатилов. – Саранск, 2016. – 36 с.
Составление расчетной схемы системы электроснабжения На рисунке 1 представлена схема системы электроснабжения, на основании ее составим расчетную схему (рис 1.1).
Рисунок 1.1 – Расчетная схема системы электроснабжения
Симметричное трехфазное короткое замыкание cyberpedia.su |
|
||||||||||||||||||
|
|
||||||||||||||||||
|




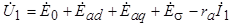 ,
,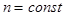 ,
, 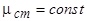 и
и 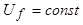 . При анализе внезапного короткого замыкания основной интерес представляют величины токов обмотки статора и характер их изменения во времени.
. При анализе внезапного короткого замыкания основной интерес представляют величины токов обмотки статора и характер их изменения во времени.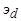 и
и 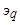 по осям d и q ротора (рис. 5.56) может быть выполнен с помощью дифференциальных уравнений магнитосвязанных контуров синхронной машины:
по осям d и q ротора (рис. 5.56) может быть выполнен с помощью дифференциальных уравнений магнитосвязанных контуров синхронной машины: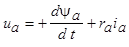 ;
; 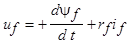 ;
;
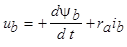 ;
; 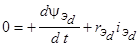 ;
;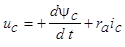 ;
; 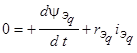 .
.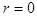 , то уравнение напряжения для него имеет вид
, то уравнение напряжения для него имеет вид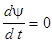
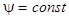 . Любые изменения потока взаимоиндукции сверхпроводящего контура вызывают протекание тока в нем такой величины и такого направления, что поле этих токов компенсирует изменение потока взаимоиндукции и поэтому результирующий поток остается неизменным.
. Любые изменения потока взаимоиндукции сверхпроводящего контура вызывают протекание тока в нем такой величины и такого направления, что поле этих токов компенсирует изменение потока взаимоиндукции и поэтому результирующий поток остается неизменным.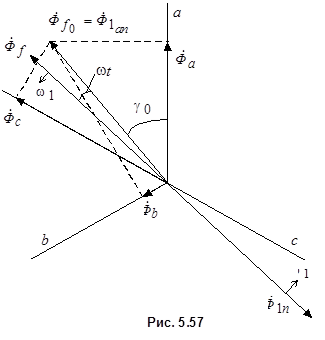
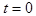 ) положение вектора потока обмотки возбуждения
) положение вектора потока обмотки возбуждения 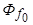 определяется углом
определяется углом 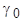 относительно фазы «а» статора (рис. 5.57). Этот поток образует с обмотками статора потокосцепления
относительно фазы «а» статора (рис. 5.57). Этот поток образует с обмотками статора потокосцепления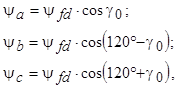
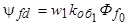 - максимальное потокосцепление фазы в момент совпадения ее магнитной оси с осью d ротора.
- максимальное потокосцепление фазы в момент совпадения ее магнитной оси с осью d ротора.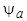 ,
, 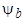 ,
, 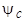 должны оставаться неизменными и при
должны оставаться неизменными и при 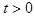 . В произвольный момент времени t положение вектора
. В произвольный момент времени t положение вектора 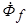 задается углом
задается углом 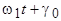 , т.е. потокосцепления фаз статора с этим потоком будут меняться с течением времени. Для того, чтобы полные потокосцепления фаз статора остались неизменными, в них должны возникнуть системы апериодических
, т.е. потокосцепления фаз статора с этим потоком будут меняться с течением времени. Для того, чтобы полные потокосцепления фаз статора остались неизменными, в них должны возникнуть системы апериодических 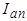 и периодических
и периодических 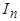 токов. Система апериодических токов
токов. Система апериодических токов 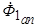 , неподвижный относительно статора и равный в первый момент короткого замыкания потоку
, неподвижный относительно статора и равный в первый момент короткого замыкания потоку 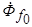 , а система периодических токов
, а система периодических токов 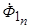 , вращающийся синхронно с потоком
, вращающийся синхронно с потоком 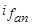 ,
, 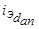 ,
, 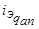 , а неподвижное поле реакции якоря
, а неподвижное поле реакции якоря 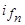 ,
, 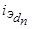 ,
, 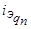 частоты
частоты 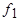 , которые постепенно затухают по мере затухания апериодических токов статора.
, которые постепенно затухают по мере затухания апериодических токов статора.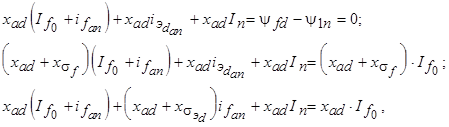
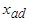 - индуктивное сопротивление реакции якоря по продольной оси;
- индуктивное сопротивление реакции якоря по продольной оси; 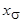 ,
, 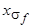 ,
, 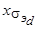 - индуктивные сопротивления обмоток статора и ротора по продольной оси.
- индуктивные сопротивления обмоток статора и ротора по продольной оси.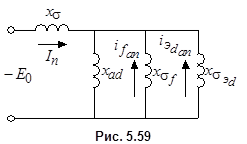
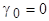 . Второе уравнение определяет потокосцепление обмотки возбуждения, а третье - потокосцепление эквивалентной демпферной обмотки по оси d. Уравнения потокосцеплений могут быть преобразованы к более удобному для анализа виду, если заменить
. Второе уравнение определяет потокосцепление обмотки возбуждения, а третье - потокосцепление эквивалентной демпферной обмотки по оси d. Уравнения потокосцеплений могут быть преобразованы к более удобному для анализа виду, если заменить 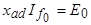 и сгруппировать члены, зависящие от
и сгруппировать члены, зависящие от 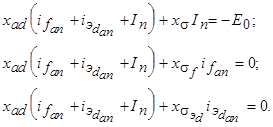
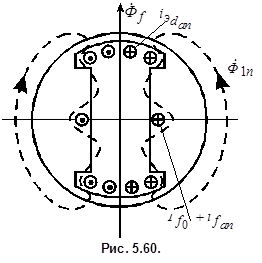
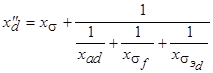
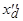 зависит, главным образом, от сопротивлений рассеяния обмоток статора и ротора. Порядок этого сопротивления
зависит, главным образом, от сопротивлений рассеяния обмоток статора и ротора. Порядок этого сопротивления 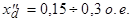 Физически малая величина сопротивления
Физически малая величина сопротивления 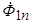 снижается, и сопротивление
снижается, и сопротивление 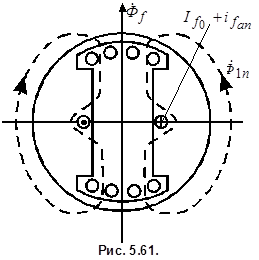
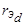 и
и 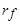 не равны нулю, то с течением времени апериодические составляющие
не равны нулю, то с течением времени апериодические составляющие 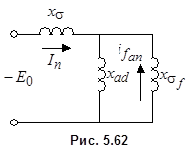
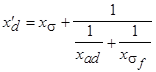
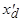 имеет большую величину,
имеет большую величину, 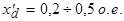
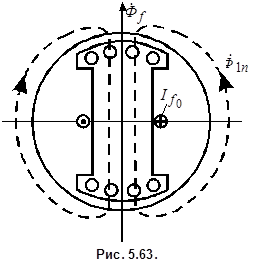
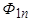 все больше проникает в ротор. Когда апериодическая составляющая тока ротора полностью затухнет, поток
все больше проникает в ротор. Когда апериодическая составляющая тока ротора полностью затухнет, поток 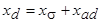
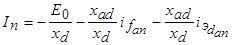 ,
,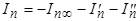 .
.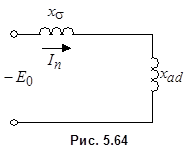
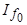 , а два других члена - составляющим тока якоря, индуцируемым апериодическими токами ротора
, а два других члена - составляющим тока якоря, индуцируемым апериодическими токами ротора 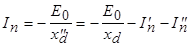 ,
,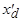 :
: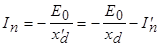 .
.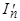 и
и 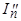 :
: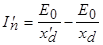 ;
; 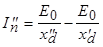 .
.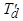 и
и 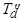 соответственно. Постоянная времени
соответственно. Постоянная времени 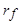 :
: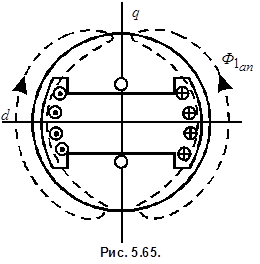
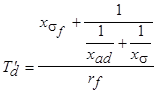 .
.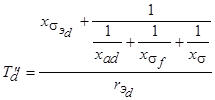 .
.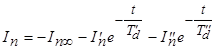 .
.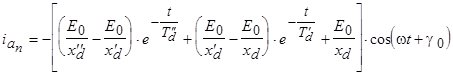 .
.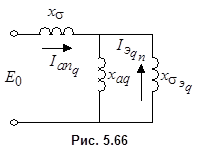
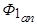 , созданный этим током, неподвижен в пространстве, поэтому при вращении ротора он будет замыкаться либо по продольной, либо по поперечной оси. Реакция ротора на внезапное появление потока по продольной оси рассмотрена выше (см. рис. 5.59). Аналогичная реакция имеет место и при возникновении потока по поперечной оси (рис. 5.65).
, созданный этим током, неподвижен в пространстве, поэтому при вращении ротора он будет замыкаться либо по продольной, либо по поперечной оси. Реакция ротора на внезапное появление потока по продольной оси рассмотрена выше (см. рис. 5.59). Аналогичная реакция имеет место и при возникновении потока по поперечной оси (рис. 5.65).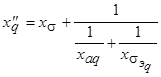
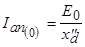 .
.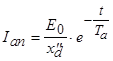 ,
,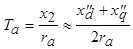 - постоянная времени обмотки статора.
- постоянная времени обмотки статора.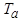 определяется индуктивным сопротивлением
определяется индуктивным сопротивлением 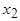 .
.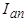 будет испытывать периодические колебания между
будет испытывать периодические колебания между 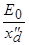 и
и 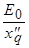 с двойной частотой:
с двойной частотой: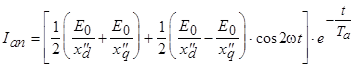 .
.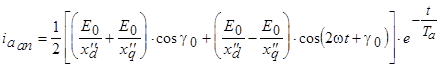 .
.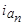 ,
, 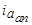 и полного тока
и полного тока 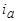 фазы при трехфазном коротком замыкании для
фазы при трехфазном коротком замыкании для 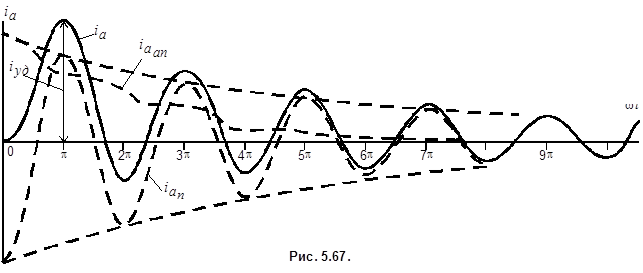
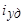 . Ток
. Ток 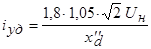 .
.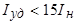 .
.



 /> — периодические составляющие, т.е. после короткого замыкания периодическая составляющая больше фазного тока до короткого замыкания и при ином угле φ.
/> — периодические составляющие, т.е. после короткого замыкания периодическая составляющая больше фазного тока до короткого замыкания и при ином угле φ.  . r после короткого замыкания уменьшилось, до короткого замыкания
. r после короткого замыкания уменьшилось, до короткого замыкания  , после короткого замыкания только
, после короткого замыкания только  . Следовательно, φ увеличится.
. Следовательно, φ увеличится. ,
,  ,
,  ,
,  ,
,  ,
,  — характеризуют предшествующий режим рассматриваемой цепи, а вертикаль t – t – неподвижная линия времени,. т.е. мгновенные значения отдельных величин определяются проекциями на эту линию соответствующих вращающихся векторов. Момент возникновения короткого замыкания определяется углом α (т.е. фазой включения) между вектором напряжения фазы А и горизонталью. (φ – угол сдвига в нормальном режиме). После включения выключателя В цепь распадается на два участка левый и правый независимые друг от друга. Правый участок зашунтирован коротким замыканием и ток в нем будет поддерживаться запасенной в индуктивности L электромагнитной энергией до тех пор, пока она не перейдет в тепло, поглощаемое активным сопротивлением. В каждой фазе правой части изменение тока описывается однородным дифференциальным уравнением:
— характеризуют предшествующий режим рассматриваемой цепи, а вертикаль t – t – неподвижная линия времени,. т.е. мгновенные значения отдельных величин определяются проекциями на эту линию соответствующих вращающихся векторов. Момент возникновения короткого замыкания определяется углом α (т.е. фазой включения) между вектором напряжения фазы А и горизонталью. (φ – угол сдвига в нормальном режиме). После включения выключателя В цепь распадается на два участка левый и правый независимые друг от друга. Правый участок зашунтирован коротким замыканием и ток в нем будет поддерживаться запасенной в индуктивности L электромагнитной энергией до тех пор, пока она не перейдет в тепло, поглощаемое активным сопротивлением. В каждой фазе правой части изменение тока описывается однородным дифференциальным уравнением: (1)
(1) (2)
(2) — начальное значение тока рассматриваемой фазы;
— начальное значение тока рассматриваемой фазы; — постоянная времени однофазной цепи.
— постоянная времени однофазной цепи.

 (3)
(3)

 , то для каждой из фаз можно записать (опуская индекс фазы А):
, то для каждой из фаз можно записать (опуская индекс фазы А): (4)
(4) (5)
(5) .
. (6)
(6) — постоянная времени цепи короткого замыкания.
— постоянная времени цепи короткого замыкания. . Второй член представляет собой (полное решение однородного уравнения) затухающий по экспоненте свободный ток или его называют апериодической слагающей тока. Начальное значение этой слагающей определяется из начальных условий, т.е.:
. Второй член представляет собой (полное решение однородного уравнения) затухающий по экспоненте свободный ток или его называют апериодической слагающей тока. Начальное значение этой слагающей определяется из начальных условий, т.е.: (7)
(7) можно найти
можно найти  .
. (8)
(8)
 и
и  на линию времени, то и ток
на линию времени, то и ток  —
—  ).
). , если в момент короткого замыкания эта слагающая (периодическая) проходит через свой положительный или отрицательный максимум. Обычно этот случай берется в качестве расчетного.
, если в момент короткого замыкания эта слагающая (периодическая) проходит через свой положительный или отрицательный максимум. Обычно этот случай берется в качестве расчетного. , т.е.
, т.е. 
 . Следовательно, из (6) получаем:
. Следовательно, из (6) получаем: (9)
(9) (10)
(10) (11)
(11)

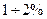 ;
; 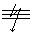 Двухфазное КЗ
Двухфазное КЗ 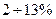 ;
; 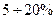 ;
; 
 Однофазное КЗ на землю
Однофазное КЗ на землю 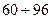 ;
; 
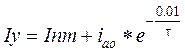 ;
; 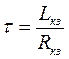
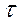 - постоянное времени затухания апериодической составляющей.
- постоянное времени затухания апериодической составляющей.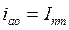
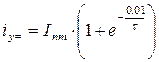
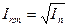
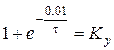 -ударный коэффициент Ку=1
-ударный коэффициент Ку=1 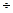 2
2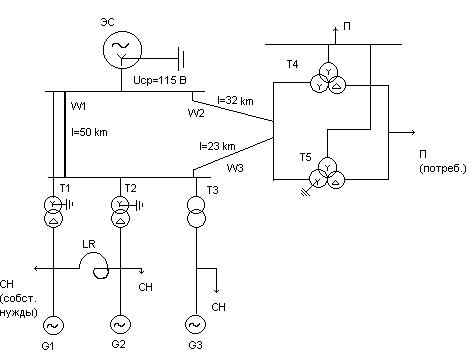
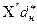 =0.146;
G3;
Sн=118 МВт;
Рн=100 МВт;
=0.146;
G3;
Sн=118 МВт;
Рн=100 МВт;