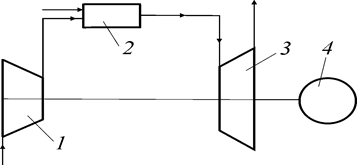
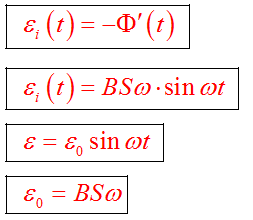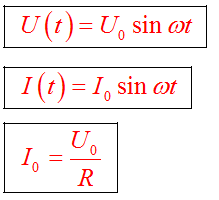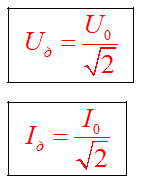Природа электрического тока. Сила тока переменногоПонятие о переменном токеЭлектрический ток бывает постоянным и переменным. Переменный – это ток, в котором среднее значение за период силы и напряжения равно нулю. Такой ток непрерывно изменяется по величине и направлению, и происходят эти изменения через равные промежутки времени.  Периодический переменный ток. Известно, что, для того чтобы вызвать в цепи переменный ток, используют генераторы переменного тока. В таких генераторах электродвижущая сила (ЭДС) возникает в процессе электромагнитной индукции. В полости цилиндрической формы вращается магнит, называемый ротором, а неподвижный сердечник с его обмоткой называется статором. Переменный ток применяется в устройствах связи (радио, телевидение, проволочная телефония и пр.), и все это благодаря тому, что напряжение и силу переменного тока можно преобразовывать почти без потери энергии. Для промышленности и освещения переменный ток вырабатывается генераторами, приводимыми во вращение водяными или паровыми турбинами и двигателями внутреннего сгорания. Переменный ток бывает однофазным и многофазным. Из многофазных широкое распространение получил трехфазный ток - система переменного тока, состоящая из трех электрических цепей, имеющих одинаковую частоту и электродвижущую силу, сдвинутые по фазе на 120°. Трехфазная система переменного тока применяется в промышленности для питания электродвигателей, электропечей, освещения.  Схема простейшего генератора переменного тока. При прохождении по проводнику переменный ток выделяет столько же тепла, сколько и постоянный. Время, в течение которого совершается одно колебание, называют периодом (обозначают буквой Т). Состояние переменного тока в отдельные моменты времени называют фазами. А число периодов в секунду – частотой. Единицей частоты является герц (Гц). Если мы говорим, что в одну секунду совершается одно колебание, то частота будет равна 1 Гц. При помощи выпрямителей переменный ток может быть преобразован в постоянный (для большинства устройств требуется постоянный ток). Долгое время в электротехнике применялся исключительно постоянный ток. Но потом возникла необходимость в передаче электроэнергии на дальние расстояния. В быту обычно используется переменный ток, поэтому мы расскажем подробнее о нем и его физических характеристиках. При передаче электроэнергии по проводам в них возникают потери, пропорциональные квадрату тока. Для уменьшения потерь необходимо уменьшить ток. Но для передачи той же мощности при меньшем токе необходимо более высокое напряжение. Поэтому передача электроэнергии на дальние расстояния может быть выполнена только при высоком напряжении. Преобразование с малыми потерями больших токов низкого напряжения в малые токи высокого напряжения, или наоборот, может производиться лишь посредством электромагнитного аппарата переменного тока — трансформатора. Поэтому в настоящее время преимущественно применяется переменный электрический ток. Ток, изменяющийся в течение определенного времени по величине и направлению, называется переменным током. Переменный ток, изменяющийся по синусоидальному закону, представляет собой однофазный синусоидальный ток:i = IM sin (wt + cp),где IM — амплитудное значение тока. Промежуток времени, в течение которого осуществляется одно полное колебание, называется периодом Т. Число периодов в секунду называется частотой, которая выражается формулойF = 1/ТЧастота измеряется в герцах (Гц). Величина w = 2яср = 2л/Т называется угловой частотой и измеряется в рад/сек; угол Zwcp называется начальной фазой. На практике наибольшее распространение получил ток, который изменяется с частотой 50 периодов в секунду, т. е. 50 Гц. Поделитесь полезной статьей: Topfazaa.ru Сила переменного токаМы видели, что мгновенное значение переменного тока все время изменяется, колеблясь между нулем и максимальным значением. Тем не менее мы характеризуем силу переменного тока, как и силу постоянного тока, определенным числом ампер. Мы говорим, например, что в одной лампочке идет ток, равный 0,25 А, а в другой, более мощной, – ток, равный 0,5 А, и т. п. Какой же смысл мы вкладываем в это утверждение? Что означает выражение «сила переменного тока»? Можно было бы характеризовать силу переменного тока его амплитудой. Принципиально это вполне возможно, но практически очень неудобно, потому что трудно построить приборы, непосредственно измеряющие амплитуду переменного тока. Удобнее использовать для характеристики переменного тока какое-нибудь свойство его, не зависящее от направления тока. Таким свойством является, например, способность тока нагревать проводник, по которому он проходит. Это нагревание не зависит от направления тока, оно производится переменным током при прохождении как в одном направлении, так и в обратном ему. Представим себе переменный ток, проходящий по некоторому проводнику с сопротивлением Сила постоянного тока, выделяющего в проводнике то же количество теплоты, что и данный переменный ток, называется действующим значением переменного тока. Из сказанного следует, что, заменив в формуле (56.1) силу постоянного тока действующим значением Подчеркнем еще раз, что в этой формуле В случае синусоидального тока действующее значение тока весьма просто связано с амплитудой этого тока. Соответствующий расчет дает, что Таким образом, измерив действующее значение синусоидального тока, можно вычислить по формуле (154.2) его амплитуду. 154.1. В проводнике, имеющем сопротивление 50 Ом, по которому шел переменный ток, за 2,5 ч выделилось количество теплоты, равное 6 кДж. Каково действующее значение тока и какова амплитуда тока? 154.2. В проводнике, имеющем сопротивление 10 Ом, переменный ток выделяет в секунду количество теплоты, равное 1 кДж. Каково действующее значение тока? 154.3. Амплитуда синусоидального переменного тока равна 5 А. Каково его действующее значение? 154.4. Действующее значение переменного синусоидального тока равно 14,2 А. Какова амплитуда этого тока? sfiz.ru Referat. Переменный ток — PhysBookПеременный токКак известно, сила тока в любой момент времени пропорциональна ЭДС источника тока (закон Ома для полной цепи). Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток. Однако в современной технике широко применяются не только источники постоянного тока, но и различные генераторы электрического тока, в которых ЭДС периодически изменяется. При подключении в электрическую цепь генератора переменной ЭДС в цепи возникают вынужденные электромагнитные колебания или переменный ток. Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника или Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону. Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону: \(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,где u – мгновенное значение напряжения, Um – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае \(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,где φc – разность (сдвиг) фаз между колебаниями силы тока и напряжения. Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц. Резистор в цепи переменного токаПусть цепь состоит из проводников с малой индуктивностью и большим сопротивлением R (из резисторов). Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление R называется активным потому, что, только на нем выделяется энергия, т.е. Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением. Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 1).  Рис. 1 Пусть напряжение на концах цепи меняется по гармоническому закону \(~u = U_m \cdot \sin \omega t\) .Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома: \(~i = \frac{U}{R} = \frac{U_m \cdot \sin \omega t}{R} = I_m \cdot \sin \omega t\) .Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 2), а амплитуда силы тока равна амплитуде напряжения, деленной на сопротивление:  Рис. 2 При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты и практически совпадает с его электрическим сопротивлением в цепи постоянного тока. Катушка в цепи переменного токаИндуктивность влияет на силу переменного тока в цепи. Это можно обнаружить с помощью простого опыта. Составим цепь из катушки большой индуктивности и лампы накаливания (рис. 3). С помощью переключателя можно присоединять эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть одинаковы. Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы тока в рассматриваемой цепи меньше силы постоянного тока.  Рис. 3 Объясняется это самоиндукцией. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь по прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех установившихся значений, которые она приобрела бы с течением времени при постоянном напряжении, равном максимальному значению переменного напряжения. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью L цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. Докажем это математически. Пусть в цепь переменного тока включена идеальная катушка с электрическим сопротивлением провода, равным нулю (рис. 4). При изменениях силы тока по гармоническому закону \(~i = I_m \cdot \cos \omega t\) .в катушке возникает ЭДС самоиндукции \(~e = -L \cdot i' = I_m \cdot L \cdot \omega \cdot \sin \omega t\) ,где L – индуктивность катушки, ω – циклическая частота переменного тока. 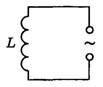 Рис. 4 Так как электрическое сопротивление катушки равно нулю, то ЭДС самоиндукции в ней в любой момент времени равна по модулю и противоположна по знаку напряжению на концах катушки, созданному внешним генератором: \(~u = -e = -I_m \cdot L \cdot \omega \cdot \sin \omega t\) .Следовательно, при изменении силы тока в катушке по гармоническому закону напряжение на ее концах изменяется тоже по гармоническому закону, но со сдвигом фазы: \(~u = I_m \cdot L \cdot \omega \cdot \cos (\omega t + \frac{\pi}{2})\) .Следовательно, колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2. В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (рис. 5). В момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. 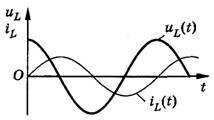 Рис. 5 Произведение \(I_m \cdot L \cdot \omega\) является амплитудой колебаний напряжения на катушке: \(~U_m = I_m \cdot L \cdot \omega\) .Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний силы тока в ней называется индуктивным сопротивлением (обозначается XL): \(~X_L = \frac{U_m}{I_m} = L \cdot \omega\) .Связь амплитуды колебаний напряжения на концах катушки с амплитудой колебаний силы тока в ней совпадает по форме с выражением закона Ома для участка цепи постоянного тока: \(~I_m = \frac{U_m}{X_L}\) .В отличие от электрического сопротивления проводника в цепи посто-янного тока, индуктивное сопротивление не является постоянной величиной, характеризующей данную катушку. Оно прямо пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в катушке при постоянном значении амплитуды колебаний напряжения должна убывать обратно пропорционально частоте. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю (XL = 0). Зависимость амплитуды колебаний силы тока в катушке от частоты приложенного напряжения можно наблюдать в опыте с генератором пере-менного напряжения, частоту которого можно изменять. Опыт показывает, что увеличение в два раза частоты переменного напряжения приводит к уменьшению в два раза амплитуды колебаний силы тока через катушку. Конденсатор в цепи переменного токаРассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы. При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения. Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы. 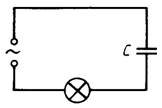 Рис. 6 Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока. При изменениях напряжения на обкладках конденсатора по гармоническому закону \(~u = U_m \cdot \cos \omega t\) ,заряд на его обкладках изменяется по закону: \(~q = C \cdot u = U_m \cdot C \cdot \cos \omega t\) .Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. Поэтому колебания силы тока в цепи происходят по закону: \(~i = -U_m \cdot \omega \cdot C \cdot \sin \omega t = U_m \cdot \omega \cdot C \cdot \cos (\omega t + \frac{\pi}{2})\) .Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на π/2 или колебания силы тока опережают по фазе колебания напряжения на π/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д.  Рис. 7 Произведение \(U_m \cdot \omega \cdot C\) является амплитудой колебаний силы тока: \(~I_m = U_m \cdot \omega \cdot C\) .Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается ХC): \(~X_C = \frac{U_m}{I_m} = \frac{1}{\omega \cdot C}\) .Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора: \(~I_m = \frac{U_m}{X_C}\) .Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте. Закон Ома для электрической цепи переменного токаРассмотрим электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки (рис. 8). Если к выводам этой электрической цепи приложить электрическое напряжение, изменяющееся по гармоническому закону с частотой ω и амплитудой Um, то в цепи возникнут вынужденные колебания силы тока с той же частотой и некоторой амплитудой Im. Установим связь между амплитудами колебаний силы тока и напряжения. 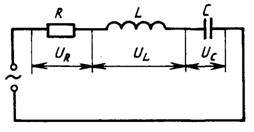 Рис. 8 В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения: \(~u = u_R + u_L + u_C\) . (1)Во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со скоростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону: \(~i = I_m \cdot \cos \omega t\) . (2)Колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, а колебания напряжения на катушке опережают по фазе колебания силы тока на π/2. Поэтому уравнение (1) можно записать так: \(~u = U_{Rm} \cdot \cos \omega t + U_{Lm} \cdot \cos (\omega t + \frac{\pi}{2}) + U_{Cm} \cdot \cos (\omega t - \frac{\pi}{2})\) , (3)где URm, UCm и ULm – амплитуды колебаний напряжения на резисторе, конденсаторе и катушке. Амплитуду колебаний напряжения в цепи переменного тока можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм. При построении векторной диаграммы необходимо учитывать, что колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, поэтому вектор, изображающий амплитуду напряжения URm, совпадает по направлению с вектором, изображающим амплитуду силы тока Im. Колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, поэтому вектор \(~\vec U_{Cm}\) отстает от вектора \(~\vec I_{m}\) на угол 90°. Колебания напряжения на катушке опережают колебания силы тока по фазе на π/2, поэтому вектор \(~\vec U_{Lm}\) опережает вектор \(~\vec I_{m}\) на угол 90° (рис. 9).  Рис. 9 На векторной диаграмме мгновенные значения напряжения на резисторе, конденсаторе и катушке определяются проекциями на горизонтальную ось векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) , вращающихся с одинаковой угловой скоростью ω против часовой стрелки. Мгновенное значение напряжения во всей цепи равно сумме мгновенных напряжений uR, uC и uL на отдельных элементах цепи, т. е. сумме проекций векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) на горизонтальную ось. Так как сумма проекций векторов на произвольную ось равна проекции суммы этих векторов на ту же ось, то амплитуду полного напряжения можно найти как модуль суммы векторов: \(~\vec U_m = \vec U_{Rm} + \vec U_{Cm} + \vec U_{Lm}\) .Из рисунка 9 видно, что амплитуда напряжений на всей цепи равна \(~U_m = \sqrt{U^2_{Rm} + (U_{Lm} - U_{Cm})^2}\) , (4)или \(~U_{m} = \sqrt{(I_m R)^2 + (I_m X_L - I_m X_C)^2} = I_m \cdot \sqrt{R^2 + (X_L - X_C)^2} = I_m \cdot \sqrt{R^2 + (L \omega - \frac{1}{C \omega})^2}\) .Отсюда \(~I_m = \frac{U_m}{\sqrt{R^2 + (L \omega - \frac{1}{C \omega})^2}}\) . (5)Введя обозначение для полного сопротивления цепи переменного тока \(~Z = \sqrt{R^2 + (L \omega - \frac{1}{C \omega})^2}\) , (6)выразим связь между амплитудными значениями силы тока и напряжения в цепи переменного тока следующим образом: \(~I_m = \frac{U_m}{Z}\) . (7)Это выражение называют законом Ома для цепи переменного тока. Из векторной диаграммы, приведенной на рисунке 9, видно, что фаза колебаний полного напряжения равна ω∙t + φ. Поэтому мгновенное значение полного напряжения определяется формулой: \(~u = U_m \cdot \cos (\omega t + \varphi)\) . (8)Начальную фазу φ можно найти из векторной диаграммы: \(~\cos \varphi = \frac{U_{Rm}}{U_m} = \frac{I_m \cdot R}{I_m \cdot \sqrt{R^2 + (L \omega - \frac{1}{C \omega})^2}} = \frac{R}{Z}\) . (9)Величина cos φ играет важную роль при вычислении мощности в электрической цепи переменного тока. Мощность в цепи переменного токаМощность в цепи постоянного тока определяется произведением напряжения на силу тока: \(~P = U \cdot I\) .Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение U∙I характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой: \(~p = u \cdot i\) .Пусть напряжение на концах цепи меняется по гармоническому закону \(~u = U_m \cdot \cos \omega t\)(с тем же успехом, разумеется, вместо \(~u = U_m \cdot \cos \omega t\) можно было бы записать \(~u = U_m \cdot \sin \omega t\)), то и сила тока будет меняться со временем гармонически с той же частотой, но в общем случае будет сдвинута по фазе относительно напряжения: \(~i = I_m \cdot \cos (\omega t + \varphi_c)\) ,где φc – сдвиг фаз между силой тока и напряжением. Поэтому для мгновенной мощности можно записать: \(~p = u \cdot i = U_m \cdot I_m \cdot \cos \omega t \cdot \cos (\omega t + \varphi_c)\) .При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период. Чтобы найти среднюю мощность за период, преобразуем полученную формулу таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов: \(~\cos \alpha \cdot \cos \beta = \frac{\cos (\alpha - \beta) + \cos (\alpha + \beta)}{2}\) .В рассматриваемом случае α = ω∙t и β = ω∙t + φc. Поэтому \(~p = \frac{U_m \cdot I_m}{2} [\cos \varphi_c + \cos (2 \omega t + \varphi_c)] = \frac{U_m \cdot I_m}{2} \cos \varphi_c + \frac{U_m \cdot I_m}{2} \cos (2 \omega t + \varphi_c)\) .Выражение для мгновенное мощности состоит из двух слагаемых. Первое не зависит от времени, а второе дважды за каждый период изменения напряжения изменяет знак: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течении другой части возвращается обратно. Поэтому среднее значение второго слагаемого за период равно нулю. Следовательно, средняя мощность Р за период равна первому члену, не зависящему от времени: \(~P = \frac{U_m \cdot I_m}{2} \cos \varphi_c\) . (10)При совпадении фазы колебаний силы тока и напряжения (для активного сопротивления R) среднее значение мощности равно: \(~P = \frac{U_m \cdot I_m}{2} = \frac{I^2_m \cdot R}{2}\) .Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = I∙U = I2∙R), вводятся понятия действующих значений силы тока и напряжения. Из равенства мощностей получим \(~P = \frac{I^2_m \cdot R}{2} =I^2 \cdot R\) или \(~\frac{I^2_m}{2} =I^2\) .Действующим значением силы тока называют величину, в \(~\sqrt{2}\) раз меньшую ее амплитудного значения: \(~I = \frac{I_m}{\sqrt{2}}\) .Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока. Аналогично можно доказать, что действующее значение переменного напряжения в \(~\sqrt{2}\) раз меньше его амплитудного значения: \(~U = \frac{U_m}{\sqrt{2}}\) .Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение (10) можно переписать: \(~P = \frac{U_m}{\sqrt{2}} \cdot \frac{I_m}{\sqrt{2}} \cos \varphi_c = U \cdot I \cos \varphi_c\) . (10)Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз φc между напряжением и током. Множитель cos φc в формуле называется коэффициентом мощности. В случае, когда φc = ± π/2 , энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при φc = - π/2 (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть. 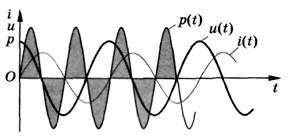 Рис. 10 Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит. При проектировании цепей переменного тока нужно добиваться, чтобы cos φc не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов. Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos φc в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φc < 0,85. Литература
www.physbook.ru Сила тока - Великие физики
Электрическим током называют направленное движение заряженных частиц в определённом направлении по проводнику. Ток в проводнике
Для того чтобы ток возник в проводнике, необходимо, чтобы в какой-то среде были свободные электрические заряды. Двигаться эти заряды заставляет некая сила F, равная величине заряда q, умноженной на напряжённость поля Е. F=q*E Направление движения положительных зарядов принимают за направление тока. Электрическое поле существует, если разность потенциалов между любыми двумя точками проводника, находящегося в этом поле, не равна нулю. Однако, в таком поле направленное движение электрических зарядов приведёт к тому, что потенциалы на концах проводника станут одинаковыми. Движение зарядов прекратится. Следовательно, исчезнет и электрическое поле. Чтобы поддержать существование электрического поля, необходимо устройство, которое называют источником тока. Источником тока могут быть батареи, аккумуляторы, электрогенераторы, солнечные батареи. Постоянный и переменный токПостоянный токПостоянным называют ток, направление и величина которого не меняются с течением времени. График постоянного тока относительно оси времени представляет собой прямую линию. Электрическое поле, с помощью которого создаётся постоянный ток в проводнике, называют стационарным. Простейший источник постоянного тока – химический элемент (аккумулятор или гальванический элемент). Направление тока в таком источнике самопроизвольно меняться не может. Переменный ток
Переменным называется ток, величина и направление которого, в отличие от постоянного тока, с течением времени меняются по определённой закономерности. Причём, эти изменения повторяются через определённые периоды времени. Если построить график переменного тока, то мы увидим, что он имеет форму синусоиды. Временной промежуток, в течение которого происходит полный цикл изменения тока, называется периодом. А число полных периодов в 1 секунду, называют частотой переменного тока. Максимальное значение тока во время полного периода называется амплитудным значением тока. Значение тока в любой выбранный момент времени называют мгновенным значением тока. Источниками переменного тока являются генераторы переменного тока. Для освещения и промышленных целей переменный ток вырабатывают мощными генераторами, которые приводятся в движение двигателями внутреннего сгорания, паровыми или водяными турбинами. Сила тока
Силой тока называют величину, равную заряду, который протекает через поперечное сечение проводника в единицу времени. В международной системе единиц (СИ) сила тока измеряется в амперах. Для участка цепи сила тока по закону Ампера прямо пропорциональна напряжению U, приложенному к участку цепи, и обратно пропорциональна сопротивлению проводника этого участка R. I = U/R Эта формула справедлива для постоянного тока. Силу тока измеряют с помощью специального прибора – амперметра. Напряжение в сети переменного тока изменяется по гармоническому закону U = Umcos ωt Переменный электрический ток в проводнике возникает под действием переменного электрического поля. Частота и фаза колебаний переменного тока совпадают с частотой и фазой колебаний напряжения. Мгновенное значение силы переменного тока выражается формулой i = Imcos ωt где i – мгновенное значение силы тока Im- амплитудное значение силы тока ω – угловая частота ω = 2πf f – частота переменного тока Амплитудное значение силы тока равно Im = Um/R Действующим значением силы переменного тока называется такое его значение, при котором средняя мощность в проводнике в цепи переменного тока равна мощности в этом же проводнике в цепи постоянного тока. IД = 1,44 Im Практически всё электрооборудование промышленных предприятий, бытовые приборы питаются от сетей переменного тока. www.phisiki.com Закон Ома.Программа КИП и А В программу «КИП и А», в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока. Сначала немного теории.. Для постоянного токаЗакон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка: Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.
Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, - "Не знаешь закон Ома, - сиди дома..". Помимо закона Ома, важнейшим является понятие электрической мощности, P: Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.
Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт. Наиболее распространенные множительные приставки:
Для переменного токаВ цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже. Импеданс, ZВ цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих. Последовательное включение R, L, C Параллельное включение R, L, CТакже, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
Коэффициент мощности, Cos(φ)Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е. Cos(φ) = P / S Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи. Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
Производные формулы:
Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу: Закон Ома для постоянного тока Закон Ома для переменного тока Расчет полного сопротивления Расчет коэффициента мощности Cos(φ)
www.axwap.com Что такое постоянный и переменный ток Движение электронов в проводнике Чтобы понимать что такое ток и откуда он берётся, нужно иметь немного знаний о строении атомов и законах их поведения. Атомы состоят из нейтронов (с нейтральным зарядом), протонов (положительный заряд) и электронов (отрицательный заряд). Электрический ток возникает в результате направленного перемещения протонов и электронов, а также ионов. Как можно направить движение этих частиц? Во время любой химической операции электроны «отрываются» и переходят от одного атома к другому. Те атомы, от которых «оторвался» электрон становятся положительно заряженным (анионы), а те к которым присоединился – отрицательно заряженными и называются катионами. В результате этих «перебеганий» электронов возникает электрический ток. Естественно, этот процесс не может продолжаться вечно, электрический ток исчезнет когда все атомы системы стабилизируются и будут иметь нейтральных заряд (отличный бытовой пример – обычная батарейка, которая «садится» в результате окончания химической реакции). История изученияДревние греки первыми заметили интересное явление: если потереть камень янтаря об шерстяную ткань, то он начинает притягивать мелкие предметы. Следующие шаги начали делать ученые и изобретатели эпохи ренессанса, которые построили несколько интересных устройств, демонстрировавших это явление. Новым этапом изучения электричества стали работы американца Бенджамина Франклина, в частности его опыты с Лейденовской банкой – первым в мире электроконденсатором. Именно Франклин ввёл понятия положительных и отрицательных зарядов, а также он придумал громоотвод. И наконец, изучение электротока стало точной наукой после описания закона Кулона. Основные закономерности и силы в электрическом токеЗакон Ома – его формула описывает взаимосвязь силы, напряжения и сопротивления. Открыт в 19м веке немецким ученым Георгом Симоном Омом. Единица измерения электросопротивления названа в его честь. Его открытия были очень полезны непосредственно для практического использования. Закон Джоуля – Ленца говорит, что на любом участке электрической цепи совершается работа. В результате этой работы нагревается проводник. Такой тепловой эффект часто используется на практике в инженерии и технике (отличный пример – лампа накаливания).  Движение зарядов при этом совершается работа Эта закономерность получила такое название потому что сразу 2 ученых примерно одновременно и независимо, вывели её с помощью опытовзакона электромагнитной индукции. В начале 19го века британский ученый Фарадей догадался, что изменяя количество линий индукции, которые пронизывают поверхность ограниченную замкнутым контуром, можно сделать индукционный ток. Посторонние силы, действующие на свободные частицы, называют электродвижущей силой (ЭДС индукции). Разновидности, характеристики и единицы измеренияЭлектрический ток может быть или переменным, или постоянным. Постоянный электроток — это ток, который не меняет своё направление и знак во времени, однако он может менять свою величину. Постоянный электроток в качестве источника чаще всего использует гальванические элементы.
Переменным называется тот, который меняет направление и знак по закону косинуса. Его характеристикой является частота. Единицы измерения в системе СИ – Герцы (Гц). В последние десятилетия очень большое распространение получил трехфазный ток. Это вид переменного тока, который включает в себя 3 цепи. В этих цепях действует переменные ЭДС одинаковой частоты, но развернутые по фазе одна относительно другой на треть периода. Фазой называют каждую отдельную электроцепь.
Сила тока зависит от величины заряда, протекающего в электроцепи за единицу времени. Сила тока это отношение электрозаряда, проходящего сквозь сечение проводника, ко времени его прохождения. В системе СИ единица измерения силы заряда – кулон (Кл), времени – секунда (с). В итоге получаем Кл/с, данную единицу называют Ампер (A). Измеряется сила электротока с помощью прибора – амперметра.
 Напряжение — это соотношение работы к величине заряда. Работа измеряется в джоулях (Дж), заряд в кулонах. Данная единица называется Вольт (В).
Показания амперметра на различных проводниках дают разные значения. А для того чтобы замерять мощность электроцепи пришлось бы использовать 3 прибора. Явление объясняется тем, что у каждого проводника различная проводимость. Единица измерения называется Ом и обозначается латинской буквой R. Сопротивление также зависит и от длины проводника.
Два проводника, которые изолированы один от второго, могут накапливать электрические заряды. Данное явление характеризуется физ. величиной, которую называют электрической емкостью. Её единицей измерения – фарад (Ф).
Работа электротока на конкретном участке цепи равняется перемножению напряжения тока на силу и время. Напряжение меряют вольтами, силу амперами, время секундами. Единицей измерения работы приняли джоуль (Дж).
Мощность электротока – это отношение работы ко времени её совершения. Мощность обозначают буквой P и измеряют ваттами (Вт). Формула мощности очень простая: Сила тока умноженная на напряжение тока.
Существует также единица именуемая ватт-час. Её не следует путать с ваттами, это 2 разные физические величины. В ваттах измеряют мощность ( скорость потребления или передачи энергии), а в ватт-часах выражается энергия произведённая за конкретное время. Это измерение часто применяют в отношении бытовых электроприборов. Например, лампа мощность которой равняется 100 Вт работала в течении одного часа, то она потребила 100 Вт*ч, а лампочка мощность которой 40 ватт потребит столько же электроэнергии за 2.5 часа. Для того, чтобы замерять мощность электроцепи используют ваттметр
Какой вид тока эффективнее и какая между ними разница?Постоянный электроток легко использовать в случае параллельного подключения генераторов, для переменного необходима синхронизация генератора и энергосистемы. В истории произошло событие под названием «Война токов». Эта «война» произошла между двумя гениальными изобретателями – Томасом Эдисоном и Николой Теслой. Первый поддерживал и активно продвигал постоянный электроток, а второй переменный. «Война» закончилась победой Теслы в 2007 году, когда Нью-Йорк окончательно перешел на переменный. Разница в эффективности передачи энергии на расстоянии оказалось огромной в пользу переменного тока. Постоянный электроток невозможно использовать, если станция находятся далеко от потребителя. Но постоянный всё равно нашел сферу применения: он широко используется в электротехнике, гальванизации, некоторых видах сварки. Также постоянный электроток получил очень большое распространение в сфере городского транспорта (троллейбусы, трамваи, метро). Естественно, не бывает плохих или хороших токов, у каждого вида есть свои преимущества и недостатки, самое главное – правильно их использовать. Похожие статьиinfoelectrik.ru Переменный электрический ток, действующее напряжение, сила тока. Мощность тока. Курсы по физикеТестирование онлайн
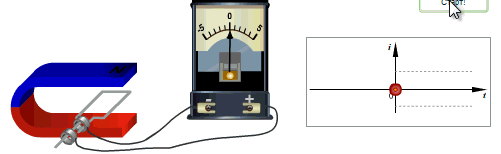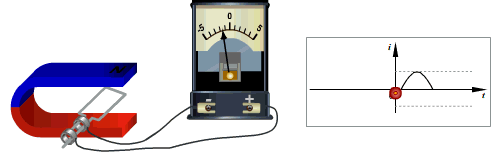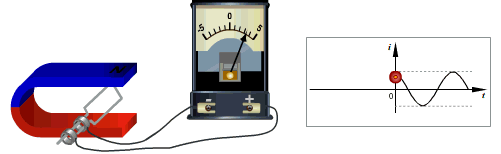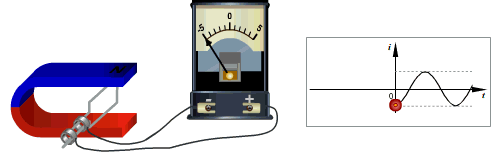
Генератор переменного токаУстройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. В основу работы генератора положено явление электромагнитной индукции.
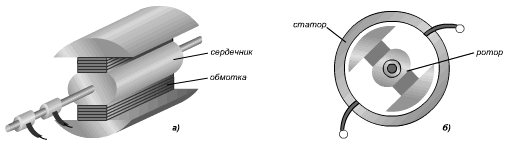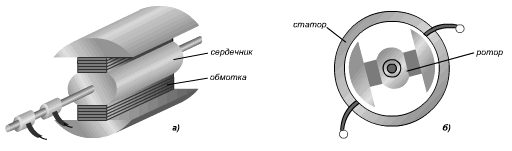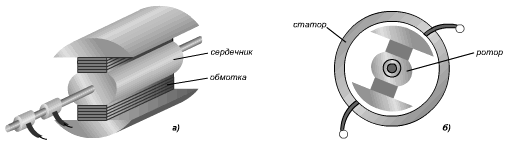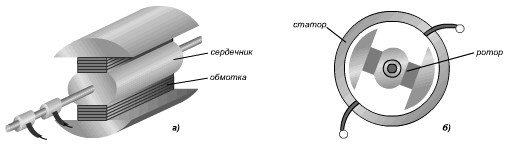
Рамка вращается в магнитном поле. Поскольку магнитный поток, пронизывающий рамку, изменяется с течением времени, то в ней возникает индуцированная ЭДС:
Ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное. Основными частями генератора переменного тока являются: индуктор, якорь, коллектор, статор, ротор.
а) устройство ротора; б) работа генератора переменного тока Переменный токПеременный ток изменяется с течением времени по гармоническому закону.
Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы такое же количество теплоты, что и данный переменный ток.
Мощность переменного токаМощность в цепи переменного тока изменяется с течением времени. Поэтому введено понятие мгновенной мощности (мощность в некоторый момент времени) и средней мощности (мощность за длительный промежуток времени).
Рассмотрим цепь переменного тока, состоящую из последовательно соединенных резистора, катушки индуктивности и конденсатора, подключенных к источнику переменного напряжения. Явление резкого увеличения амплитуды переменного тока в такой цепи получило название резонанса напряжений. Частота, при которой наблюдается резонанс, называется резонансной частотой.
Резонансная частота равна частоте свободных колебаний контура. fizmat.by | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|




 . В течение секунды ток выделяет в проводнике определенное количество теплоты, скажем
. В течение секунды ток выделяет в проводнике определенное количество теплоты, скажем  . Пропустим через тот же проводник постоянный ток, подобрав силу его так, чтобы он выделял в проводнике ежесекундно то же количество теплоты
. Пропустим через тот же проводник постоянный ток, подобрав силу его так, чтобы он выделял в проводнике ежесекундно то же количество теплоты  .
.  . (154.1)
. (154.1)  . (154.2)
. (154.2) 




 Почти все современные генераторы производят трёхфазный электроток.
Почти все современные генераторы производят трёхфазный электроток.