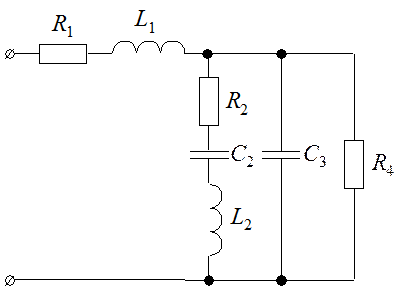
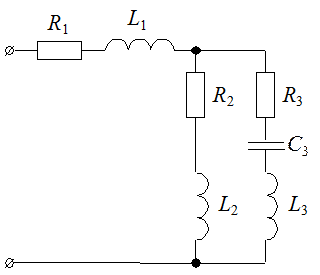
2.2. Методика расчета однофазных линейных электрических цепей переменного токи. Расчет однофазной цепи переменного тока3. Расчет однофазной цепи переменного тока3.1. Задание для самостоятельной работыДля цепи синусоидального тока заданы параметры (табл. 8) включенных в нее элементов (рис. 10) и действующее значение напряжения на ее зажимах; частота питающего напряжения f = 50 Гц. Необходимо: 1) определить действующие значения тока в ветвях и неразветвленной части цепи символическим методом; 2) по полученным комплексным изображениям записать выражения для мгновенных значений тока в ветвях и напряжения на участке цепи с параллельным соединением; 3) построить упрощенную векторную диаграмму; 4) составить баланс мощности; 5) определить характер (индуктивность или емкость) и параметры элемента, который нужно добавить в неразветвленную часть схемы, чтобы в цепи имел место резонанс напряжений; 6) выполнить моделирование режима работы цепи при заданных параметрах и в режиме резонанса напряжений с помощью системы схемотехнического моделирования Electronics Workbench. 3.2. Методические указания к выполнению аналитического расчета3.2.1. Рассмотрим порядок расчета однофазной цепи переменного тока на примере анализа схемы, представленной на рис. 11, а. Числовые значения параметров указаны в табл. 9. Расчет однофазной цепи с одним источником выполняют методом эквивалентных преобразований («сворачиванием» – «разворачиванием») схемы, который рассмотрен в разд. 1. Перед выполнением расчетов необходимо значения всех параметров привести к международной системе единиц СИ (1 мГн = 10-3 Гн; 1 мкФ = 10-6 Ф). Расчет ведется символическим методом с помощью аппарата комплексных чисел. 1 2 3 4 5 6 7 EMBED Word.Picture.8 EMBED Word.Picture.8 8 9 0 Рис. 10 Таблица 8 Числовые значения параметров элементов схемы
Таблица 9 Числовые значения параметров элементов схемы для примера расчета
Для расчета полных комплексных сопротивлений ветвей определим реактивные составляющие сопротивлений (рис. 11, б), которые создают реактивные элементы, находящиеся в ветвях. Реактивное сопротивление индуктивного элемента , емкостного –, общее сопротивление ветви, содержащей индуктивный и емкостный элементы, –, гдерад; f = 50 Гц – частота питающего напряжения. Первая ветвь цепи не содержит реактивного элемента, поэтому реактивная составляющая сопротивления ветви будет равна нулю: Ом. Вторая ветвь содержит два реактивных элемента. Общее реактивное сопротивление ветви равно алгебраической сумме индуктивного и емкостного сопротивлений. Знак «плюс» ставится у индуктивного сопротивления, «минус» – у емкостного:
Знак «минус» перед общим реактивным сопротивлением ветви указывает на его емкостный характер. Этот знак сохраняется и при записи полного комплексного сопротивления (см. ниже). а б в г д Рис. 11 Реактивное сопротивление третьей ветви
Полные комплексные сопротивления ветвей в алгебраической, показательной и тригонометрической форме (см. рис. 11) имеют вид: , (59) где R – действительная составляющая комплексного сопротивления; Х – мнимая составляющая комплексного сопротивления; –модуль комплексного сопротивления; –аргумент комплексного сопротивления, знак аргумента зависит от знака реактивного сопротивления ветви. Для ветвей рассматриваемой электрической цепи ; (60) Ом; ; (61) Ом; ; (62) Ом. Эквивалентная схема с учетом выполненных расчетов представлена на рис. 11, в. Последующие операции «сворачивания» электрической схемы основаны на рассмотренных в первом разделе свойствах параллельного и последовательного соединений. Нужно помнить, что сложение и вычитание комплексных чисел выполняется в алгебраической форме записи, а умножение и сложение – в показательной, если расчеты ведутся на калькуляторе. Заменим параллельный участок на эквивалентное сопротивление (рис. 11, г): ; (63)
Последовательное соединение двух сопротивлений преобразуем в простейшую цепь (рис. 11, д): ; (64) Ом. Полученная элементарная цепь рассчитывается по закону Ома для цепей переменного тока: Напряжение на параллельном участке
Токи в параллельных ветвях рассчитываются по выражениям: Для построения векторной диаграммы необходимо также определить напряжение на неразветвленной части цепи:
Расчет однофазной цепи с помощью математического редактора Mathсad представлен в прил. 3. Нужно заметить, что в Mathсad операции с комплексными числами выполняют в алгебраической форме записи. Для определения модулей и аргументов комплексных чисел нужно выполнить дополнительные команды. Углы в Mathсad вычисляются в радианах. Для перехода в градусную меру измерения углов необходимо дополнительно указать оператор: «deg» (см. прил. 3). Результаты расчетов занесите в графу «Расчет» табл. 10. Таблица 10 Полученные значения токов и напряжений для рассматриваемой цепи
3.2.2. Мгновенные значения тока в ветвях и напряжения можно записать с учетом того, что амплитудное значение тока в раз больше действующего значения, которое равно модулю полученного комплексного числа:
3 Рис. 12 .2.3. Для проверки правильности расчетов строят векторную диаграмму токов и напряжений электрической цепи. Необходимо выбрать масштаб по току, А/мм, и по напряжению, В/мм, построить систему ортогональных осей комплексной плоскости (+1, +j). Векторы тока и напряжения строят из начала координат так, чтобы длина вектора была равна модулю комплексного числа (действующему значению) с учетом масштаба, а угол наклона к действительной оси (+1) – аргументу комплексного числа (начальной фазе), причем положительные углы откладываются против часовой стрелки, отрицательные – по часовой. Векторная диаграмма для рассматриваемого примера приведена на рис. 12.Если на векторной диаграмме сумма векторов токов параллельных ветвей равна вектору тока в неразветвленной части цепи в соответствии с первым законом Кирхгофа для узловой точки, а сумма векторов напряжения – напряжению источника, то считается, что диаграмма сходится, и это обязательное, но не достаточное условие для вывода о правильности расчетов. 3.2.4. Окончательно о правильности полученных результатов можно судить по балансу мощности, который для цепей переменного тока может быть составлен для комплексов полной мощности источника и потребителей: , (75) или для активной и реактивной мощностей как составляющих. Выполним проверку по балансу активной и реактивной мощностей: где ,– угол сдвига фаз между приложенным напряжением и током в неразветвленной части цепи, он зависит от нагрузки цепи и равен аргументу полного комплексного сопротивления; ; , где – действующие значения токов, т. е. модули комплексных чисел, изображающих соответствующие токи; , реактивное сопротивление берется с учетом знака. Активная мощность всегда положительна, реактивная может быть и отрицательной. Знак «минус» указывает на то, что реактивная мощность отдается цепью в сеть, а не потребляется из сети. Для рассматриваемого примера: Вт; Вт; вар;
В результате баланс активной мощности: 1297 Вт = 1297 Вт, а реактивной: – 1105 вар = – 1105 вар. Баланс активной и реактивной мощности выполняется, следовательно, расчет однофазной цепи выполнен верно. 3.2.5. Резонанс напряжений в цепи наступает тогда, когда реактивное сопротивление цепи равно нулю. Если реактивное сопротивление цепи носит индуктивный характер (), то необходимо в неразветвленную часть цепи добавить емкостное сопротивление, значение которого равно индуктивной составляющей сопротивления: (77) . (78) Если реактивное сопротивление цепи носит емкостный характер (), то необходимо в неразветвленную часть цепи добавить индуктивное сопротивление: (79) . (80) В рассматриваемом примере ; реактивная составляющая сопротивления – емкостная. Рассчитаем индуктивное сопротивление, которое обеспечит в цепи резонанс напряжений:
studfiles.net Расчет однофазной цепи переменного тока3. расчет однофазной цепи переменного тока 3.1. Задание для самостоятельной работы Для цепи синусоидального тока заданы параметры (табл. 8) включенных в нее элементов (рис. 10) и действующее значение напряжения на ее зажимах; частота питающего напряжения f = 50 Гц. Необходимо: 1) определить действующие значения тока в ветвях и неразветвленной части цепи символическим методом; 2) по полученным комплексным изображениям записать выражения для мгновенных значений тока в ветвях и напряжения на участке цепи с параллельным соединением; 3) построить упрощенную векторную диаграмму; 4) составить баланс мощности; 5) определить характер (индуктивность или емкость) и параметры элемента, который нужно добавить в неразветвленную часть схемы, чтобы в цепи имел место резонанс напряжений; 6) выполнить моделирование режима работы цепи при заданных параметрах и в режиме резонанса напряжений с помощью системы схемотехнического моделирования Electronics Workbench. 3.2. Методические указания к выполнению аналитического расчета 3.2.1. Рассмотрим порядок расчета однофазной цепи переменного тока на примере анализа схемы, представленной на рис. 11, а. Числовые значения параметров указаны в табл. 9. Расчет однофазной цепи с одним источником выполняют методом эквивалентных преобразований («сворачиванием» – «разворачиванием») схемы, который рассмотрен в разд. 1. Перед выполнением расчетов необходимо значения всех параметров привести к международной системе единиц СИ (1 мГн = 10-3 Гн; 1 мкФ = 10-6 Ф). Расчет ведется символическим методом с помощью аппарата комплексных чисел.
3 4 5 6 7 8 9 0 Рис. 10 Таблица 8 Числовые значения параметров элементов схемы
Таблица 9 Числовые значения параметров элементов схемы для примера расчета
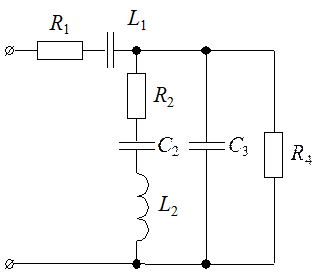
Для расчета полных комплексных сопротивлений ветвей определим реактивные составляющие сопротивлений (рис. 11, б), которые создают реактивные элементы, находящиеся в ветвях. Реактивное сопротивление индуктивного элемента Первая ветвь цепи не содержит реактивного элемента, поэтому реактивная составляющая сопротивления ветви будет равна нулю: vunivere.ru 2.2. Методика расчета однофазных линейных электрических цепей переменного токиК зажимам электрической цепи, схема замещения которой приведена на рис. 2.31, подключен источник синусоидального напряжения В частотойf = 50 Гц. Параметры элементов схемы замещения: R1 = 5 Ом, R2 = 8 Ом, L1 - 39,8 мГн, L2 = 19 мГн, С1 = 162,5 мкФ, С2 = 192 мкФ. Выполнить следующее: 1) определить реактивные сопротивления элементов цепи; 2) определить действующие значения токов во всех ветвях цепи; 3) записать уравнение мгновенного значения тока источника; 4) составить баланс активных и реактивных мощностей; 5) построить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений; 6) результаты расчетов занесем в соответствующие таблицы.
Дано: R1 = 5 Ом, R2 = 8 Ом, L1 - 39,8 мГн, L2 = 19 мГн, С1 = 162,5 мкФ, С2 = 192 мкФ. Определить: XL1, XL2, XC1, XC2, I, I1, I2, I3, I4, i. 1) Реактивные сопротивления элементов Рис.2.31 цепи:
2) Расчет токов в ветвях цепи выполняем методом эквивалентных преобразований. Представим схему, приведенную на рис. 2.31. в следующем виде:
Рис. 2.32 Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:
Выразим действующее значение напряжений в комплексной форме:
Вычисляем токи ветвей и общий ток цепи:
или
Для определения токов параллельных ветвей ирассчитаем напряжение на зажимах этих ветвей.
3) Уравнение мгновенно значения тока источника:
4) Комплексная мощность цепи: , где
(знак минус определяет емкостной характер нагрузки в целом) Активная иреактивная мощность приемников:
Баланс мощностей выполняется:
или в комплексной форме:
где
- баланс практически сходится. 5) Напряжение на элементах схемы замещения цепи:
6) Строим топографическую векторную диаграмму на комплексной плоскости. Выбираем масштаб: Определяем длины векторов токов и напряжений:
На комплексной плоскости в масштабе откладываем векторы токов в соответствии с расчетными значениями, при этом положительные фазовые углы отсчитываем от оси (+1) против часовой стрелки, а отрицательные - по часовой стрелке. Так, вектор тока повернут относительно оси(+1) на угол 120,6° и длина его , вектор токасовпадает с действительной осью и длина егои т. д. Топографическая векторная диаграмма напряжений характерна тем, что каждой точке диаграммы соответствует определенная точка электрической цепи. Построение векторов напряжений ведем, соблюдая порядок расположения элементов цепи и ориентируя векторы напряжений относительно векторов тока: - на активном сопротивлении ток и напряжение совпадают по фазе; - на индуктивном элементе напряжение опережает ток на 90°; - на емкостном напряжение отстает от тока на 90°. Направление обхода участков цепи выбираем, как принято, противоположно положительному направлению токов. Обход начинаем от точки "b", потенциал которой принимаем за исходный (φb=0). Точку "b" помещаем в начало координат комплексной плоскости. При переходе от точки "b" к точке "e" потенциал повышается на величину падения напряжения на емкостном сопротивлении XC1. Вектор этого напряжения отстает по фазе от вектора токана 90º. Конец вектора, определяет потенциал точки"e". Потенциал точки "d" выше, чем потенциал точки "е", на величину падения напряжения . Вектороткладываем от точки"е" параллельно вектору тока . Конецопределяет потенциал точки"d". Соединив отрезком прямой "b" и "d", получим вектор напряжения на зажимах цепи . Аналогично строим векторы напряжений других участков цепи, сохраняя обход навстречу току. От точки "b" проводим вектор параллельно вектору. Конец вектораопределяет потенциал точки"с". От точки "с" откладываем вектор , опережающий вектор токана 90°, т. к. участок"ас" содержит индуктивное сопротивление XL2. Затем от точки "a" откладываем вектор , опережающий вектор токана 90°. Конецопределяет потенциал точки"d". Соединив отрезком прямой "b" и "a", получим вектор напряжений . 6) Результаты расчетов занесем в соответствующие таблицы Результаты расчетов реактивных сопротивлений
Результаты расчетов токов
studfiles.net Символический (комплексный) метод расчета цепей переменного токаОдним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):
Рис.1. Вращающийся вектор С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ
имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно,
имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно,
и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат) и тогда
и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно,
Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно. 2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)
Рис.2. Комплексное число на комплексной плоскости Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна
На рисунке выше этот вектор также показан.Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли
При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.Итак, три формы записи комплексного числа: 1) показательная форма в виде
2) тригонометрическая форма в виде
3) алгебраическая форма
где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая. Например, имеем комплексное число в показательной форме вида
в тригонометрической форме записи это запишется как
при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что
В итоге получим
где При переходе от алгебраической формы к показательной комплексное число вида
переходит к показательному виду по следующим преобразованиям
а угол
Таким образом, и получим
Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:
Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.
Рис.3. Схема с последовательным соединением элементов Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):
Рис.4. Схема с комплексными обозначениями По закону Ома ток в цепи равен
где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как
Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида
Соответственно, комплекс входного напряжения в показательной форме запишется как
Полное комплексное сопротивление цепи в общем виде
Находим комплексное сопротивление индуктивности
Находим комплексное сопротивление емкости
Соответственно, общее комплексное сопротивление цепи
Ток в цепи
Комплексные напряжения на элементах
Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство Проверяем
С небольшим расхождением из-за округлений промежуточных вычислений всё верно. Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:1) полное сопротивление электрической цепи и его характер;2) действующие значения токов в ветвях;3) показания вольтметра и ваттметра;
Рис.5.Цепь однофвзного синусоидального тока Решение:1. Находим комплексные сопротивления ветвей и всей цепи:Учитываем, что
Комплексное сопротивление первой ветви:
Комплексное сопротивление второй ветви:
Комплексное сопротивление третьей ветви:
Общее сопротивление цепи
Откуда
2. Находим действующие значения токов в ветвях:
Рис.6. Схема с обозначенными комплексными токами
Действующие значения, соответственно,
3. Определим показания приборов:Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:U=220 ВВаттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:
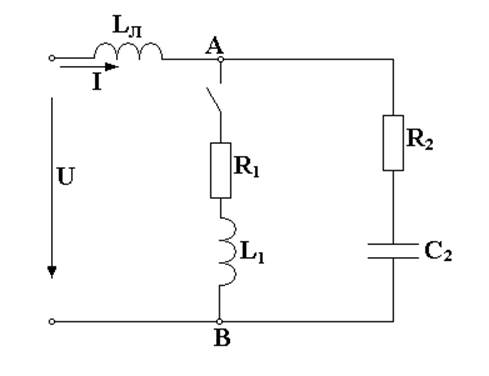
electrikam.com Расчет и анализ однофазной цепи переменного тока (U = 500 В, ƒ = 50 Гц, Lл = 25 мГн)Новосибирский государственный архитектурно-строительный университет (Сибстрин) Кафедра строительных машин, автоматики и электротехники Индивидуальное задание №2 Вариант № 0 РАСЧЕТ И АНАЛИЗ ОДНОФАЗНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА Выполнила студентка гр. 219 Б Вепрева Анна Проверила ст. преподаватель Осипова Л.Б. Новосибирск-2008
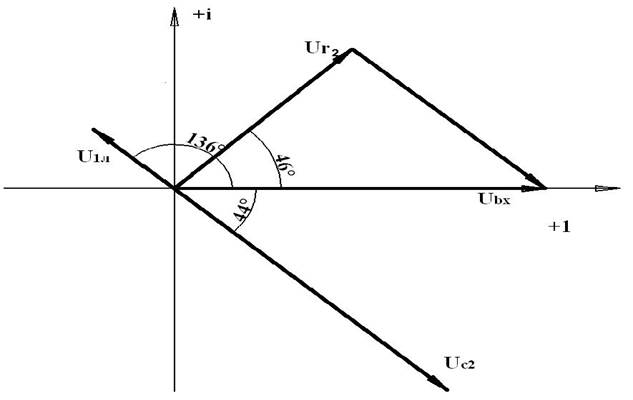
ƒ= 50 Гц LЛ = 25 мГн R1 = 12 Ом R2 = 18 Ом L1 = 151 мГн C2 = 119 мкФ I. а) Ключ разомкнут, до резонанса напряжений. Полное комплексное сопротивление цепи: Z= R2 + jXLл – jXС2 Реактивные сопротивления катушки и конденсатора : XLл = w·LЛ = 2πƒLЛ = 314,16*·25·10-3 = 7,85 Ом XC2 = 1/(w·С2) = 1/(314,16·119·10-6) = 26,75 Ом Z = 18 + j(7,85 – 26,75) = 18 – j18,9 = 26,1e-j46,4° Ом Ток в последовательной цепи : I = Uвх/Z = 500/26,1e-j46,4° = 19,16 e j46,4° = =19,16·cos 46,4° + j19,16·sin 46,4° = 13,21 + j13,88 A Падения напряжения на участках цепи: UR2 = I·R2 = 19,16ej46,4°·18 = 344,88 e j46,4°В UC2 = -jXC2·I = 26,75· e-j90° 19,16e j46,4°· = 512,53e-j43,6° B ULл = jXLл·I = 7,85ej90°·19,16e j46,4° = 150,41e j136,4° B Полная кажущаяся мощностьS = U·I* = 500·(13,21 – j13,88) = 6605 – j6940 BA = 9580,7 e-j46,4° BA Векторная диаграмма: МU= 50В/см; МI= 4А/см
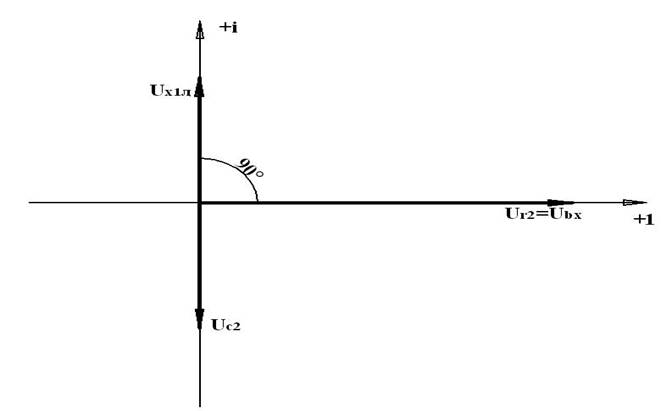
I. б) Ключ разомкнут, резонанс напряжений. Резонанс напряжений выражается в том, что полное сопротивление контура становится наименьшим и равным активному сопротивлению, а ток становится максимальным. Условием резонанса напряжений является равенство индуктивного и емкостного сопротивлений для токагенератора: XLл = XC2 w·LЛ = 1/(w·C2P) =>C2P = 1/(w2·Lл) = 405,7 мкФ Ток в последовательной цепи во время резонанса напряжений: IP = U/(R2 + jXL – jXC2р) = U/R2 = 500/18 = 27,78 A Падение напряжения на участках цепи: UXL = IP·jXLл = 27,78·7,85ej90° = 218,06ej90°B UC2 = -jXC2р·IP = 27,78·7,85e-j90° = 218,06e-j90° B UR2 = R2·IP = 18·27,78 = 500 B Полная мощность : S = I*·U = 500·27,78 = 13890 Вт или по другой формуле S = R2·IP2=18 * 27,782= 13891 Вт Векторная диаграмма: МU= 50В/см; МI= 4А/см
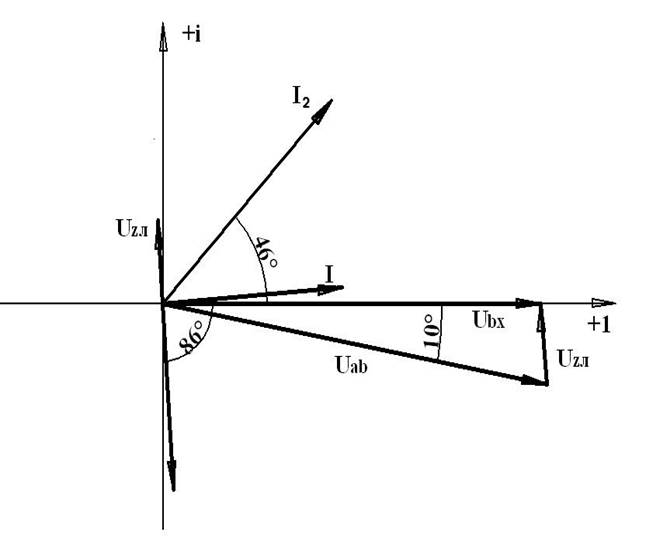
II. а) Ключ замкнут, до резонанса токов. Реактивное сопротивление катушки в 1-й ветви: XL1 = w·L1 = 2πƒL1 = 314,16*·151·10-3 = 47,44 Ом Полные комплексные сопротивления 3-х ветвей: ZЛ = jXLл = 7,85 ej90° Ом Z1 = R1 + jXL1 = 12 + j47,44 = 48,93 ej75,8° Ом Z2 = R2 – jXC2 = 18 – j26,75 = 32,24 e-j56,06° Ом Эквивалентное сопротивление параллельных ветвей ZАВ = Z1* Z2 /( Z1+ Z2) = =(48,93ej75,8° *32,24e-j56,06°) / (12 + j47,44+18 – j26,75 ) = = (1577,5* e j19,74)/(30+ j 20,69) =(1577,5* e j19,74)/(36,44* e j34,6) = =43,29* e –j14,86=43,29*cos(-14,86) + j43,29*sin(-14,86)=41,84– j11,1 А Общее сопротивление схемы: Zобщ = ZАВ + ZЛ = 41,84– j11,1 + j7,85 = 41,84 – j3,25 = 41,97e-j4,44° Ом Ток в неразветвленной части цепи: Iобщ = U/Zобщ = 500/41,97e-j4,44° = 11,91ej4,44° = 11,87+j0,92 A Напряжение на зажимах параллельных ветвей: UAB = Iобщ·ZAB = 11,91ej4,44°·43,29e-j14,86° = 515,58e-j10,42° B Токи ветвей: I1 = UAB/Z1 = 515,58e-j10,42°/48,93ej75,8°=10,54e-j86,22° = 0,69 – j10,52 A I2 = UAB/Z2 = 515,58e-j10,42°/32,24e-j56,06° = 16ej45,64° A Полная мощность: S=I*·U = 500·(11,87 – j0,92) = 5935 – j460 = 5952,8 e-j4,44° BA PQ Р -активная мощность (Вт) , Q– реактивная мощность (ВАр) Падение напряжения в линии: UZл = jXLл·I = 11,91ej4,44°·7,85ej90° = 93,45ej94,44° B Векторная диаграмма: МU= 50В/см; МI= 2А/см
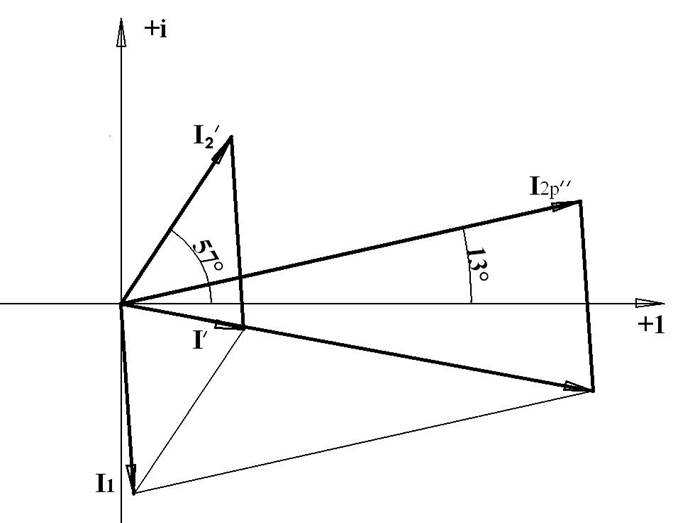
II. б) Ключ замкнут, резонанс токов. Физический признак резонанса токов –минимальный ток, потребляемый источником ( ток в линии ). Явление полезное в силовых цепях, т.к. уменьшаются потери мощности DP=Rл* Iл2. Условие резонанса токов: реактивная проводимость ветви с катушкой должна быть равна реактивной проводимости ветви с конденсатором: BL= BC [ Сименс ] XL1/(R21 + X2L1) = XC2/(R22 + X2C2р) Решаем квадратичное уравнение относительно XC2р 47,44/(144 + 2250,55) = XC2р/(324 + X2C2р) 15370,56 + 47,44X2C2р = 2394,55XC2р X2C2р – 50,48XC2 + 324 = 0 D = 2548,23 – 1296 = 1252,23 X'C2 = 42,93 Ом X"C2 = 7,55 Ом Определим емкость конденсатора, обеспечивающую нужное реактивное сопротивление 2-й ветви: C2P' = 1/(w·X’C2р) = 1/(314,16*·42,93) = 74,15·10-6 Ф C2P" = 1/(w·X”C2р) = 1/(314,16*·7,55) = 421,6·10-6 Ф Новое полное комплексное сопротивление 2-й ветви с новым конденсатором : Z'2P = R2 – jX'C2р = 18 – j 42,93 = 46,55e-j67° Ом Z"2P = R2 – jX"C2р = 18 – j 7,55e-j23° Ом= 19,52 e-j22,75° Ток во 2-й ветви с новым конденсаторомI'2P = UAB/Z'2P = 515,58e-j10,42°/46,55e-j67° = 11,08ej56,83° = 11,08·cos 56,83° + j11,08 sin 56,83°= 6,06 + j 9,27 A I"2P = UAB/Z"2P = 515,58e-j10,42°/19,52e-j22,75° = 26,41ej12,33° = 26,41 ·cos 12,33° + j·26,4 sin 12,33° = 25,8 + j 5,64 A Ток в неразветвленной части цепи (в линии): I' = I1 + I'2P= 0,69 – j10,52 + 6,06 + j 9,27 A= 6,75 – j 1,25= 6,86е-j10,49°А I" = I1+ I"2P= 0,69 – j10,52 + 25,8 + j 5,64 A= 26,49 – j 4,88= 26,94е-j10,44°А Сравнивая ток в линии при наличии во 2-й ветви 3-х различных конденсаторов (11,91ej4,44°А при С2=119 мкФ; 6,86 е-j10,49°А при C'2P = 74,15·10-6 Ф и 26,94 е-j10,44°А при C"2P = 421,6·10-6 Ф ), выбираем конденсатор, обеспечивающий минимальный ток в линии C'2P = 74,15·10-6 Ф. Векторная диаграмма: МU= 50В/см; МI= 2А/см
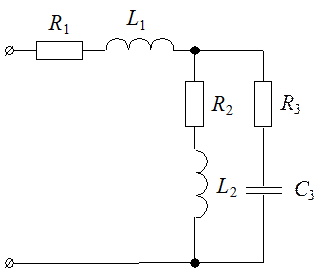
vunivere.ru РАСЧЕТ ОДНОФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА«РАСЧЕТ ОДНОФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА» На рисунке приведена схема однофазной электрической цепи. В таблице приведены значения параметров элементов и закон изменения напряжения на входе схемы. Необходимо определить: законы изменения токов на участках цепи; действующие значения напряжений и токов в ветвях схемы; коэффициент мощности цепи и её отдельных ветвей; активную, реактивную и полную мощность в ветвях и всей цепи; условия, при которых на заданных участках наступит резонанс напряжений или токов. Построить топографическую и векторную диаграммы напряжений и токов.
Рис.1 Схема электрическаяДано:
Рис.2: Преобразованная схемаРешение: Начальные данные:
1). Найдем сопротивления
2). Найдем действительные напряжения:
Найдем общее сопротивление:
3). Найдем токи:
4). Уравнение токов:
5). Напряжения в ветвях цепи:
6). Мощности на участках цепи:
7). Полная мощность:
8). Условия, наступления резонанса напряжений и токов:
-резонансное 9).Значения для топографической диаграммы:
studfiles.net Расчет однофазной цепи переменного тока. Вариант № 2Архангельский государственный технический университет Институт информационных технологий Кафедра электротехники Расчетно – графическая работа №1 «Расчет однофазной цепи переменного тока» Вариант № 43. Выполнила: студентка ИИТ-III-1 Тарарышкина А.С. Проверил: Архангельск 2002
Рассчитываем недостающие параметры. Z0= -j*8 = 8*e-j90 = 8*(cos(-90)+j*sin(-90)) Z1= 1 – j*3 = 3,16*e-j71,56 = 3,16*(cos(-71,56)+j*sin(-71,56)) Z2 = 1 + j*3 = 3,16*ej71,56 = 3,16*(cos(71,56)+j*sin(71,56)) I1= 10,7 + j*12,9 = 16,76*ej50,32 = 16,76*(cos(50,32)+j*sin(50,32)) 1. U1=I1*Z1=(16,76*ej50,32)*( 3,16*e-j71,56) = 52,96*e-j21,24 Uab = U2 = U1 = 49,36 - j*19,18 = 52,96*e-j21,24 = 52,96*(cos(-21,24)+j*sin(-21,24)) 2. I2 = U2/Z2 = (52,96*e-j21,24)/( 3,16*ej71,56) = 16,76*e-j92,8 I2 = -0,82 - j*16,74 = 16,76*e-j92,8 = 16,76*(cos(-92,8)+j*sin(-92,8)) 3. I0 = I1+I2 = (10,7 + j*12,9)+( -0,82 - j*16,74) = 9,88 - j*3,84 I0 = 9,88 - j*3,84 = 10,6*e-j21,24 = 10,6*(cos(-21,24)+j*sin(-21,24)) 4. U0 = I0*Z0 = (10,6*e-j21,24)*( 8*e-j90) = 84,8*e-j111,24 U0 = -30,72 - j*79,04 = 84,8*e-j111,24 = 84,8*(cos(-111,24)+j*sin(-111,24))
5. Zab = (Z1*Z2)/(Z2+Z1) Z1*Z2 = (3,16*e-j71,56)*( 3,16*ej71,56) = 9,98*e0 = 9,98 Z1+Z2 = (1 – j*3)+( 1 + j*3) = 2+j*0 = 2 Zab = 9,98/2 = 4,99 Zab = 4,99 + j*0 = 4,99*e0 = 4,99*(cos(0)+j*sin(0)) Z = Zab + Z0 = (4,99 + j*0) + (0 - j*8) = 4,99 - j*8 Z = 4,99 - j*8 = 9,43*e-j58,04 = 9,43*(cos(-58,04) + j*sin(-58,04)) U = I*Z =(10,6*e-j21,24)*( 9,43*e-j58,04) = 99,96*e-j79,28 U = U0 + Uab = (-30,72 - j*79,04) + (49,36 - j*19,18) = 18,64 - j*98,22 Проверка правильности расчетов законами Кирхгофа. I0 = I1 + I2 => I0 – I1 – I2 = 0 (9,88 - j*3,84) – (10,7 + j*12,9) – (-0,82 - j*16,74) = 0 Расчет комплекса полной мощности (S) и ее составляющих P, Q. S = U*I = U*I(cosa + j*sina) = P + j*Q S = (99,96*e-j36,8)*( 10,6*e-j21,24) = 1059,57*e-j58,04 = 1059,57*(cos(-58,04) + j*sin(-58,04)) = 560,86 - j*898,96 P = 560,86 Вт Q = 898,96 Вар Расчёт ёмкости и индуктивности при частоте f = 50 Гц, для имеющихся конденсаторов и катушек индуктивности. L,C -? XC0 = 8 Ом XC0 = 1/2πfC0 => C0 = 1/2πf XC0 C0 = 1/8*2*50*3,145 = 0,00039788 Ф XC1 = 3 Ом XC1 = 1/2πfC1 => C1 = 1/2πf XC1 C1 = 1/3*2*50*3,145 = 0,001061033 Гн XL = 3 Ом XL = 2πfL => L = XL/2πf L = 3/2*3,145*50 = 0,00955 Гн vunivere.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|




 1 2
1 2 
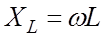 , емкостного –
, емкостного – 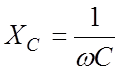 , общее сопротивление ветви, содержащей индуктивный и емкостный элементы, –
, общее сопротивление ветви, содержащей индуктивный и емкостный элементы, – 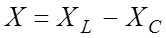 , где
, где 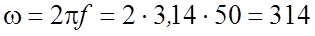 рад;f = 50 Гц – частота питающего напряжения.
рад;f = 50 Гц – частота питающего напряжения. 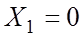 Ом.
Ом.






 .
.


















 при φ = 0° равно
при φ = 0° равно
















 — нагрузка носит активно-индуктивный характер
— нагрузка носит активно-индуктивный характер



 U = 500 B
U = 500 B