Напряженность электрического поля. Напряженность обозначениеФормула напряжённости электрического поля Здесь Единица измерения напряжённости электрического поля – В/м (вольт на метр) или Н/Кл (ньютон на кулон). Напряжённость – векторная величина, характеризующая интенсивность воздействия электрического поля на заряжённую частицу в конкретной точке. Напряжённость поля в различных точках вообще говоря различна, то есть электрическое поле – это векторное поле, направление векторов которого зависит от того, как было создано это поле. По указанной формуле можно рассчитать не только силу воздействия электрического поля на точечный заряд, но и силу воздействия этого поля на заряжённое тело, если распределение заряда в нём известно.  Примеры решения задач по теме «Напряжённость электрического поля»
ru.solverbook.com Напряженность электрического поля - это... Что такое Напряженность электрического поля?Напряжённость электрического по́ля — векторная характеристика электрического поля в данной точке, равная отношению силы , действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q: .По сути, задает само векторное поле, поскольку его величина и направление меняется в пространстве от точки к точке. Напряжённость электрического поля точечного зарядаДля системы СИИспользуя потенциал Вектор выражается как градиент потенциала, взятый с обратным знаком: . К примеру, для точечного заряда, исходя из закона Кулона . Так как эквипотенциальные поверхности являются в этом случае сферами, то производная по нормали есть производная по радиусу. Таким образом мы можем прийти к так называемому кулоновскому полю:; .Используя теорему Остроградского — Гаусса Из формулы Остроградского-Гаусса вектор можно определить, зная плотность распределения зарядов. Согласно Формуле О-Г, а также используя уравнение Максвелла , легко получить: где qin — заряд, находящийся внутри замкнутой поверхности S, объемом V. В качестве поверхности интегрирования возьмем сферу (центральная симметрия), тогда И самоочевидно: .Как и следовало ожидать, результаты полностью совпали. Для системы СГСРассуждения аналогичны, вся разница лишь в том, что изменяется вид потенциала , уравнение Максвелла и . В итоге, получаем в системе СГС: Системы единицВ системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в Ньютонах на Кулон или в Вольтах на метр (В/м или V/m). См. такжеWikimedia Foundation. 2010. dic.academic.ru Напряжённость электрического поля - это... Что такое Напряжённость электрического поля?Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный[1]пробный заряд, помещенный в данную точку поля, к величине этого заряда : .Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном[2] множителе). В каждой точке пространства в данный момент времени существует свое значение вектора (вообще говоря - разное[3] в разных точках пространства), таким образом, - это векторное поле. Формально это выражается в записи представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к. может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле[4], и законы, которым оно подчиняется, есть предмет электродинамики. Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон. Напряжённость электрического поля в классической электродинамикеИз сказанного выше ясно, что напряженность электрического поля - одна из основных фундаментальных величин классической электродинамики. В этой области физики можно назвать сопоставимыми с ней по значению только вектор магнитной индукции (вместе с вектором напряженности электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал). Приведем краткий обзор основных контекстов классической электродинамики в отношении напряженности электрического поля. Сила, с которой действует электромагнитное поле на заряженные частицыПолная сила, с которой электромагнитное поле (включающее вообще говоря электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца: где q - электрический заряд частицы, - ее скорость, - вектор магнитной индукции (основная характеристика магнитного поля), косым крестом обозначено векторное произведение. Формула приведена в единицах СИ. Как видим, эта формула полностью согласуется с определением напряженности электрического поля, данном в начале статьи, но является более общей, т.к. включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля. В этой формуле частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов - надо только воспользоваться обычным для физики приемом разбиения сложного тела на маленькие (математически - бесконечно маленькие) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы. Остальные формулы, применяемые для расчета электромагнитных сил (такие, как, например, формула силы Ампера) можно считать следствиями[5] фундаментальной формулы силы Лоренца, частными случаями ее применения итп. Однако для того, чтобы эта формула была применена (даже в самых простых случаях, таких, как расчет силы взаимодействия двух точечных зарядов), необходимо знать (уметь рассчитывать) и чему посвящены следующие параграфы. Уравнения МаксвеллаДостаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряженности электрического поля: Здесь - плотность заряда, - плотность тока, - универсальные константы (уравнения здесь записаны в единицах СИ). Здесь приведена наиболее фундаментальная и простая форма уравнений Максвелла - так называемые "уравнения для вакуума" (хотя, вопреки названию, они вполне применимы и для описания поведения электромагнитного поля в среде). Подробно о других формах записи уравнений Максвелла - см. основную статью. Этих четырех уравнений вместе с пятым - уравнением силы Лоренца - в принципе достаточно, чтобы полностью описать классическую (то есть не квантовую) электродинамику, то есть они представляют ее полные законы. Для решения конкретных реальных задач с их помощью необходимы еще уравнения движения "материальных частиц" (в классической механике это законы Ньютона), а также зачастую дополнительная информация о конкретных свойствах физических тел и сред, участвующих в рассмотрении (их упругости, электропроводности, поляризуемости итд итп), а также о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом. «Материальные уравнения»Такими дополнительными формулами или уравнениями (обычно не точными, а приближенными, зачастую всего лишь эмпирическими), которые не входят непосредственно в область электродинамики, но поневоле используются в ней ради решения конкретных практических задач, называемыми «материальными уравнениями», являются, в частности:
Связь с потенциаламиСвязь напряженности электрического поля с потенциалами в общем случае такова: где - скалярный и векторный потенциалы. Приведем здесь для полноты картины и соответствующее выражение для вектора магнитной индукции: В частном случае стационарных (не меняющихся со временем) полей, первое уравнение упрощается до: Это выражение для связи электростатического поля с электростатическим потенциалом. ЭлектростатикаВажным с практической и с теоретической точек зрения частным случаем в электродинамике является тот случай, когда заряженные тела неподвижны (например, если исследуется состояние равновесия) или скорость их движения достаточно мала чтобы можно было приближенно воспользоваться теми способами расчета, которые справедливы для неподвижных тел. Этим частным случаем занимается раздел электродинамики, называемый электростатикой. Как мы уже заметили выше, напряженность электрического поля в этом случае выражается через скалярный потенциал как или то есть электростатическое поле оказывается потенциальным полем. ( в этом случае - случае электростатики - принято называть электростатическим потенциалом).
Уравнения поля (уравнения Максвелла) при этом также сильно упрощаются (уравнения с магнитным полем можно исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона: а в областях, свободных от заряженных частиц - к уравнению Лапласа: Учитывая линейность этих уравнений, а следовательно применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряженность поля, создаваемого любым распределением зарядов (суммируя решения для точечного заряда). Теорема ГауссаОчень полезной в электростатике оказывается теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла: где интегрирование производится по любой замкнутой поверхности S (вычисляя поток через эту поверхность), Q - полный (суммарный) заряд внутри этой поверхности. Эта теорема дает крайне простой и удобный способ расчета напряженности электрического поля в случае, когда источники имеют достаточно высокую симметрию, а именно сферическую, цилиндрическую или зеркальную+трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости. Напряжённость электрического поля точечного зарядаВ единицах СИДля точечного заряда в электростатике верен закона Кулона или . .Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность S в виде сферы с центром в точечном заряде, учесть, что направление будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r: , имеем: откуда сразу получаем ответ для E. Ответ для получается тогда интегрированием E: Для системы СГСФормулы и их вывод аналогичны, отличие от СИ лишь в константах. Напряженность электрического поля произвольного распределения зарядовПо принципу суперпозиции для напряженности поля совокупности дискретных источников имеем: где каждое Подставив, получаем: Для непрерывного распределения аналогично: где V - область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство, - радиус-вектор точки, для которой считаем , - радиус-вектор источника, пробегающий все точки области V при интегрировании, dV - элемент объема. Можно подставить x,y,z вместо , вместо , вместо dV. Системы единицВ системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское В/м, международное V/m). ЛитератураПримечания
См. такжеdic.academic.ru Обозначение - напряжение - Технический словарь Том IIОбозначение напряжения указывает, что трансформатор предназначен для работы в трехфазной системе при соединении трех трансформаторов в звезду. Обмотки ВН, расположенные на двух стержнях трансформатора, соединены последовательно, что требует установки двух переключателей. Расположение вводов и переключателей на крышке трансформатора показано на рис. 5 - 33 г. Переключатели имеют пять положений переключения, которые обозначаются на крышке римскими цифрами I-V. Ступень номинального напряжения обычно соответствует положению III переключателя. В табл. 5 - 8 приведено положение переключателей, соответствующее той или другой ступени напряжения. Параметры гетеродинных ЛОВ см я мм вочн с магнитной и электростатической фокусировками. Обозначения напряжений V и Jnp соответствуют схемам рнс. Обозначение напряжения текучести CTS также индексировано, дополнительно цифрами 1, 2 и 3 в зависимости от участка, к которому оно относится; as3 относится к исходному металлу при той средней температуре, которую он имеет в приемнике. Для обозначения напряжений, действующих на всех шести гранях элемента, были использованы три символа: GX -, 0V GZ Для нормальных напряжений и шесть символов: т, тхг, т тг / г zjfi tzy - для касательных. При обозначении напряжения в индексах первой буквой будет обозначаться электрод, потенциал которого определяется, а второй буквой - электрод, потенциал которого принят за точку отсчета. Такой способ обозначения напряжений обычен при решении плоских задач. Однако он не согласуется с общим правилом, требующим, чтобы выполнялось условие о о а з - Необходимо помнить, что когда главные напряжения в плоскости имеют одинаковый знак, то наибольшее касательное напряжение в рассматриваемой точке лежит не в этой плоскости. В дальнейшем к обозначениям напряжения текучести ь и коэффициента трения ц будут добавляться индексы участков, так как величины 0S и ц по участкам в общем случае различны. Здесь штрих в обозначениях напряжений и токов означает, что эти величины относятся к режиму обратного питания четырехполюсника. Индекс / при обозначениях напряжений указывает, что напряжения вызываются силами инерции. На рис. 7.8 показано обозначение напряжений в полярных координатах. При построении рассматриваемой диаграммы правило обозначения ных напряжений частично нарушается. В дальнейшем индекс max в обозначениях напряжений будем опускать, имея в виду, что рассматриваются максимальные напряжения цикла. Индекс ft введен в уравнение для обозначения напряжений от изменения температуры. Индекс & введен в уравнение для обозначения напряжений от изменения температуры.В дальнейшем изложении используется вторая система обозначения напряжений.На рис. 5, а, б показаны обозначения напряжений на площадках, нормальных к остальным дзум осям.Сигнальный знак для кабельного перехода. Диск окрашивается красной краской, полоса - белой. Открыто проложенные кабели должны быть снабжены бирками с обозначением напряжения, сечения, номера или наименования линии.Для упрощения записи далее скобка ( р) после обозначений напряжений и токов, указывающая на операторную форму уравнений, опущена.Цепи освещения и управления переключают перестановкой разъемных перемычек на клеммы с обозначением напряжения, соответствующего напряжению внешней сети.Циклические напряжения - синоним многократно приложенных и переменных напряжений, употребляется для обозначения напряжений, возникающих под действием периодически повторяющихся по определенному циклу нагрузок.Приступая к изучению напряженного состояния тела, прежде всего введем такую систему обозначения напряжений, которая позволила бы легко различать напряжения на различных площадках, проведенных в данной точке, и была бы возможно более мнемо-ничной.Радиальные окружные напряжения в крышках и днищах определяют по соответствующей расчетной схеме; выражения для напряжений приведены в табл. 11.5. Нижний индекс при обозначении напряжения соответствует направлению деформаций ( радиальное р, окружное t), индекс за скобками - виду нагружения.Радиальные окружные напряжения в крышках и днищах определяют по соответствующей расчетной схеме; выражения для напряжений приведены в табл. 11.5. Нижний индекс при обозначении напряжения соответствует направлению деформаций ( радиальное р, окружное /), индекс за скобками - виду нагружения.Напряжения ах, ау дем две. На рис. 3.5 показаны обе системы напряжений при плоском напряженном состоянии, главные напряжения ог и сг2 и напряжения ах, ау и гху: Обозначения напряжений с буквенными и цифровыми индексами были приведены в гл. Обозначения с цифровыми индексами удобны для сокращения записи формул.Не забывая тот факт, что входные и выходные напряжения и токи в схемах зависят от времени, с целью упрощения записи формул время в обозначениях напряжений и токов будем опускать.Изгиб железобетонного бруска. Здесь Еж - коэффициент пропорциональности, называемый модулем нормальной или продольной упругости железа ( он равен 2 - 106 кг / см2), а индекс ж при обозначениях напряжения и относительного удлинения показывает, что эти величины относятся к железной арматуре. Равенство (5.1) справедливо лишь до некоторого напряжени ( порядка 2500 кг / см2), которое носит название предел, пропорциональности. Обозначения напряжений, токов и параметров обмоток такие же, что и в других уравнениях.Пусть ось Ох параллельна действующему на этой грани напряжению. Будем употреблять, как обозначение напряжения символ Хх - Это удобно, так как X будет представлять собой напряжение, направление которого параллельно Ох, а значок внизу у X будет определять направление той поверхности, по которой действует рассматриваемое напряжение. Напряжение на заштрихованной грани будет вполне определено, если мы дадим Хх некоторое определенное значение.Напряжения на. Для передней грани ( направление внешней нормали противоположно направлению оси у) положительное касательное напряжение направлено противоположно оси г. Разумеется, векторы напряжений приложены по всем шести граням элемента. Па рис. 2.10 показаны обозначения напряжений в цилиндрической системе координат. Нормальные напряжения тг называются радиальными, ов - окружными напряжениями.Разность напряжений до пуска и в момент пуска электродвигателя для какой-либо точки сети представляет собой колебание напряжения в этой точке. Колебание напряжения обозначается буквой б, поставленной перед обозначением напряжения.Разность между величинами напряжений двух точек сети называется потерей напряжения на участке сети между этими точками. Потеря напряжения обозначается буквой Д, поставленной перед обозначением напряжения с индексами, соответствующими точкам сети, между которыми определяется потеря напряжения.Схемы замещения катушки и конденсатора при параллельном соединении. Вектор направляется к точке, стоящей цервой в обозначении напряжения.К задаче.| Схемы замещения цепи параллельного соединения катушки индуктивности и конденсатора. Вектор направляется к точке, стоящей первой в обозначении напряжения.Основные типы деформирования трещины. ( а тип I, ( Ь тип II, ( с тип III. Используя методы, разработанные Вестергором [13], Ирвин [14] получил выражения для напряжений и деформаций для каждого из изображенных на рис. 3.27 типов трещины в случае двумерного напряженно-деформированного состояния. При этом он использовал координаты, изображенные на рис. 3.28. Обозначения напряжений пояснены в разд.Ручные переносные светильники в помещениях с повышенной опасностью должны применяться напряжением 36 в, а в помещениях особо опасных-12 в. Светильники должны подключаться только с помощью штепсельной вилки в розетку сети с обозначением напряжения 12 или 36 в. Понижающие трансформаторы должны иметь раздельные обмотки первичного и вторичного напряжения. Один из выводов вторичной обмотки должен заземляться.Как видно из структурных схем ( рис. 3.2, а в), принципиальных отличий между транзисторами противоположной проводимости не существует; разница заключается лишь в перемене полярности подключаемых источников питания, что в свою очередь приводит к изменению направлений токов. Из условных обозначений ( рис. 3.2 б г) видно, что в названиях токов принято указывать индекс соответствующего вывода, а в обозначениях напряжений - индексы переходов.Если плоскость А движется в направлении, указанном стрелкой, относительно плоскости Б, то на гранях элементарного кубика возникают сдвиговые, или касательные, напряжения, вызывающие его скашивание. В полимерах, проявляющих высокоэла-стичность - большие обратимые деформации, при сдвиге кроме касательных возникают и нормальные напряжения, направленные перпендикулярно граням элементарного кубика. Оси координат на рисунке обозначены цифрами, а для обозначения напряжений использованы индексы, состоящие из двух цифр; первая из них указывает, на какой грани кубика действует напряжение, а вторая - направление действия напряжений. Напряжения в крышке и днище ротора определяют нием напряжений от воздействия давления жидкости, центробежных сил, краевых сил и моментов; деформации элементов также рассчитывают в зависимости от напряжения иагружения по формулам для быстровращающихся дисков или плоских круглых пластин. Радиальные окружные напряжения в крышках и днищах определяют по соответствующей расчетной схеме; выражения для напряжений приведены в табл. 11.5. Нижний индекс при обозначении напряжения соответствует направлению деформаций ( радиальное р, окружное /), индекс за скобками - виду нагружения.Например, напряжение, ранее обозначаемое ах -, будет теперь иметь вид а ц, а под а12 будет подразумеваться касательное напряжение txa. В табл. 2.1 представлены рядом обе системы обозначения напряжений - буквенная и цифровая, причем в буквенной для простоты и общности опущены штрихи. Цифровая система индексов имеет то преимущество, что позволяет осуществить сокращенную запись напряжений.Предположим, что на образовавшуюся при испарении или сублимации межфазную поверхность нанесены насечки глубиной порядка нескольких атомных расстояний таким образом, что они образуют замкнутую линию. Для сохранения механического равновесия к атомам, располагающимся вдоль условных насечек, следует приложить внешние силы. Ясно, что они действуют перпендикулярно к контуру насечек и лежат в плоскости, касательной к поверхности раздела жидкость - газ. Произведение этих внешних сил, действующих на некотором участке насечек, на длину его контура представляет собой поверхностную энергию жидкости а, часто именуемую поверхностным натяжением. Этот термин используют также для обозначения напряжений в поверхностном слое неупругих тел. Согласно определению, поверхностное натяжение является вектором, лежащим на нормали к обводу участка, и действующим по касательной к поверхности раздела фаз. www.ai08.org | ||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|




![Rendered by QuickLaTeX.com \[ E = \frac{F}{q} \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5e82887d8df5ee47cf35b75e59a91ab8_l3.png)
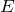 – напряжённость электрического поля,
– напряжённость электрического поля, 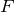 – сила, действующая на заряд,
– сила, действующая на заряд, 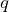 – величина заряда.
– величина заряда.









