Мощность в цепи постоянного тока. Мощность в цепиМощность в цепи постоянного тока
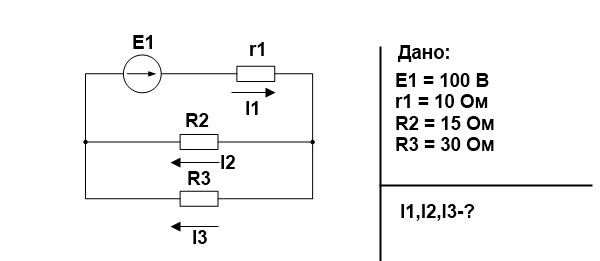
Для удобства я сразу напишу международные обозначения этих четырёх величин: U – напряжение (В, вольт) I – ток (А, ампер) R – сопротивление (Ом, ом) P – мощность (Вт, ватт – не надо путать с вольтом, который обозначается только одной буквой В)  В абстрактном примере – чем больше магазин (напряжение) и чем меньше вам шепчет совесть (сопротивление), тем больше вы тратите денег (сила тока), а когда вы несёте купленный товар домой, вы совершаете работу (мощность). Мощность в цепи постоянного тока это и есть работа, совершаемая электричеством. Мощность это произведение тока на напряжение, а если вместо тока или напряжения подставить соответствующие значения, то можно получить мнемоническую табличку: Как видите, мощность в цепи постоянного тока это довольно простое понятие, если немного вдуматься в материал. По сути, это всего две формулы с заменой значений. Как это выглядит: Если теперь в формуле мощности подставить место значения тока формулу тока, то получим следующее: Именно таким образом и получилось 12 формул на основе закона Ома, которые вы видите в мнемонической табличке. Что такое мощность в цепях постоянного тока мы более или менее разобрались, но есть ещё один момент. Баланс мощностей в цепи постоянного тока.Собственно, это просто проверка правильности расчетов электрической цепи. Возвращаясь к нашему абстрактному примеру это выглядит так: вы купили товары, забрали их на кассе, отошли от кассы и вам показалось, что ваши пакеты должны быть больше или меньше, чем получились. Тогда вы берёте чек и начинаете сравнивать товар в чеке и товар в наличии. Если товары в чеке и товары в руках совпали, значит всё в порядке. Если мы обратимся к определению, то баланс мощностей – сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. Как это использовать на практике? Допустим, у нас есть задача, которую нужно решить: Поскольку решение задачи не является целью этой статьи, я дам уже готовые ответы. Теперь надо проверить правильно ли были посчитаны токи в задаче. Ток в цепи равен току , следовательно, мощность источника питания (Е1хI1) должна быть равна сумме мощностей сопротивлений Что мы и получаем с учетом потерь при округлениях. Таким образом, баланс мощностей в электрической цепи постоянного тока — это ничто иное, как проверка самого себя, своих расчётов. Как видите, мощность в цепи постоянного тока посчитать довольно легко. Гораздо больше сложностей возникнет, если ток будет переменный. Другими словами, на примере магазина это выглядит так: Постоянный ток – от входа до выхода прямая линия и вы спокойно идете от начала и до конца без каких-либо приключений. Переменный ток – магазин представляет из себя зигзаг и вам приходится делать лишние движения. Поэтому в переменном токе мощность считать немного сложнее, но это уже тема совсем другой статьи. Поделиться ссылкой:
Похожееuelektrika.ru Т. Мощность в цепи пер. тока — PhysBookМощность в цепи переменного токаЕсли напряжение в цепи переменного тока \(~U = U_0\sin wt,\) то мгновенное значение мощности переменного тока равно произведению мгновенных значений силы тока и напряжения \(~P = IU = I_0\sin \left( wt - \varphi\right)U_0\sin wt.\) Выполнив преобразование тригонометрической функции \(~\sin \left( wt - \varphi\right),\) получим \(~P = I_0U_0 \left( \sin^2 wt \cos \varphi - \sin wt \cos wt \sin \varphi \right).\)Практический интерес представляет среднее по времени значение мощности. Если учесть, что \(~\mathcal h \sin^2 wt \mathcal i = \frac {1}2\) и \(~\mathcal h \sin wt \cos wt \mathcal i = 0,\) то среднее значение мощности за период будет равно \(~\mathcal h P \mathcal i = \frac {I_0 U_0}2 \cos \varphi \Rightarrow \mathcal h P \mathcal i = I_d U_d \cos \varphi,\)где Id и Ud — действующие значения силы тока и напряжения. Множитель \(~\cos \varphi\) называют коэффициентом мощности. Последняя формула показывает, что мощность, выделяемая на участке цепи, состоящем из последовательно соединенных резистора, катушки и конденсатора переменного тока, зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Из рисунка 1 видно, что \(~\cos \varphi = \frac {U_{0R}}{U_0} = \frac {I_0 R}{I_0 Z} = \frac RZ.\) 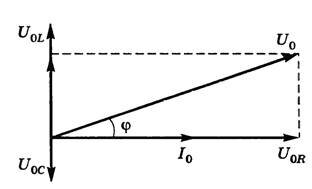 Рис. 1 Подставим в формулу средней мощности значение коэффициента мощности \(~\mathcal h P \mathcal i = \frac {I_d U_d R}{Z}.\) Но по закону Ома \(~I_d = \frac {U_d}{Z}.\) Следовательно, \(~\mathcal h P \mathcal i = I^2_d R = \frac {I^2_0}2 R.\)Таким образом, средняя мощность в цепи переменного тока равна средней мощности, выделяемой на активном сопротивлении R (см. Переменный ток). Это активная мощность, т.е. средняя мощность необратимых превращений в цепи переменного тока. Уменьшение \(~\cos \varphi \) приводит не только к неполному использованию мощности генератора электростанций (часть энергии возвращается в сеть — это реактивная мощность), но и к увеличению тепловых потерь в цепи (так как \(~ I = \frac {\mathcal h P \mathcal i}{U \cos \varphi},\) то \(~\Delta P = I^2 R = \frac {\mathcal h P^2 \mathcal i R}{U^2 \cos^2 \varphi}\)). Повышение коэффициента мощности электрических установок является важной народнохозяйственной задачей. ЛитератураАксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 408-409. www.physbook.ru Электрическая мощность - это... Что такое Электрическая мощность?Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Мгновенная электрическая мощностьМгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи. По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем: Для единичного заряда на участке A-B: Для всех зарядов: Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем: Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности: мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке: Если участок цепи содержит резистор c электрическим сопротивлением R, то Дифференциальные выражения для электрической мощностиМощность, выделяемая в единице объёма, равна: В линейном изотропном приближении: В линейном анизотропном приближении (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла): Мощность постоянного токаТак как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле: Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать: Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:
Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой. Мощность переменного токаВ переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока. Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения. Активная мощностьЕдиница измерения — ватт (W, Вт). Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью. Реактивная мощностьЕдиница измерения — вольт-ампер реактивный (var, вар) Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: . Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду. Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными. Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.[источник не указан 124 дня] Полная мощностьЕдиница полной электрической мощности — вольт-ампер (V·A, В·А) Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Векторная зависимость между полной, активной и реактивной мощностью выражается формулой: Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах. Комплексная мощностьМощность, аналогично импедансу, можно записать в комплексном виде: где — комплексное напряжение, — комплексный ток, — импеданс, * — оператор комплексного сопряжения.Модуль комплексной мощности равен полной мощности S. Действительная часть равна активной мощности Р, а мнимая — реактивной мощности Q с корректным знаком в зависимости от характера нагрузки. Неактивная мощностьНеактивная мощность (пассивная мощность)[источник не указан 172 дня] — это мощность нелинейных искажений тока, равная корню квадратному из разности квадратов полной и активной мощностей в цепи переменного тока. В цепи с синусоидальным напряжением неактивная мощность равна корню квадратному из суммы квадратов реактивной мощности и мощностей высших гармоник тока[источник не указан 172 дня]. При отсутствии высших гармоник неактивная мощность равна модулю реактивной мощности. Под мощностью гармоники тока понимается произведение действующего значения силы тока данной гармоники на действующее значение напряжения[источник не указан 172 дня]. Наличие нелинейных искажений тока в цепи означает нарушение пропорциональности между мгновенными значениями напряжения и силы тока, вызванное нелинейностью нагрузки, например когда нагрузка имеет реактивный или импульсный характер. При линейной нагрузке сила тока в цепи пропорциональна мгновенному напряжению, вся потребляемая мощность является активной. При нелинейной нагрузке увеличивается кажущаяся (полная) мощность в цепи за счёт мощности нелинейных искажений тока, которая не принимает участия в совершении работы[источник не указан 172 дня]. Мощность нелинейных искажений не является активной и включает в себя как реактивную мощность, так и мощность прочих искажений тока. Данная физическая величина имеет размерность мощности, поэтому в качестве единицы измерения неактивной мощности можно использовать В∙А (вольт-ампер) или вар (вольт-ампер реактивный). Вт (ватт) использовать нежелательно, чтобы неактивную мощность не спутали с активной. Связь неактивной, активной и полной мощностейВеличину неактивной мощности обозначим N. Через i обозначим вектор тока, через u — вектор напряжения. Буквами I и U будем обозначать соответствующие действующие значения: Представим вектор тока i в виде суммы двух ортогональных составляющих ia и ip, которые назовём соответственно активной и пассивной. Поскольку в совершении работы участвует только составляющая тока, коллинеарная напряжению, потребуем, чтобы активная составляющая была коллинеарна напряжению, то есть ia = λu, где λ — некоторая константа, а пассивная — ортогональна, то есть Имеем Запишем выражение для активной мощности P, скалярно умножив последнее равенство на u: Отсюда находим Выражение для величины неактивной мощности имеет вид где S = U I — полная мощность. Для полной мощности цепи справедливо представление, аналогичное выражению для цепи с гармоническими током и напряжением, только вместо реактивной мощности используется неактивная мощность: Таким образом, понятие неактивной мощности представляет собой один из способов обобщения понятия реактивной мощности для случая несинусоидальных тока и напряжения. Неактивная мощность иногда называется реактивной мощностью по Фризе. Измерения
Мощность некоторых электрических приборовВ таблице указаны значения мощности некоторых потребителей электрического тока:
Большинство бытовых приборов рассчитаны на напряжение 220 В, но на разную силу тока. Поэтому мощность потребителей электроэнергии разная. Литература
Дополнительная литература
СсылкиСм. такжеdikc.academic.ru Мощность, выделяемая в цепи переменного токаМгновенное значение мощности переменного тока равно произведению мгновенного значения напряжения на силу тока: , где и . Раскрыв , получим . Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что , , получим:
где , поэтому среднее значение мощности будет равно:
Такую же мощность развивает постоянный ток: . Величины и называются действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градируются по действующим значениям тока и напряжения. Учитывая действующие значения тока и напряжения, выражение средней мощности (4.5.1) можно записать в виде:
где множитель называется коэффициентом мощности. Формула (4.5.4) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае, зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи отсутствует реактивное сопротивление Х, то и . Если цепь содержит только реактивное сопротивление (R = 0), то и средняя мощность равна нулю, какими бы большими ни были ток и напряжение. Если имеет значение существенно меньше единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приводит либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить . Наименьшее допустимое значение для промышленных установок составляет примерно 0,85. В таблице 4.1 приведены сравнительные характеристики механических и электромагнитных колебаний. Таблица 4.1
ens.tpu.ru Мощность в цепи постоянного и переменного токаМощность в цепи постоянного и переменного тока. В цепи постоянного тока мощность потребляемая нагрузкой определяется по формуле: Опр. Среднюю за период мощность, потребляемую нагрузкой, для этого в начале найдём мгновенную мощность электрического тока в нагрузке. Нагрузка, потребляющая эл. энергию (мощность).
Из ф. 2 видно, что мгновенная мощность содержит постоянную составляющую и переменную гармоническую составляющую удвоенной частоты. Найдём ср.мощность по ф. 1.
Здесь U и I действующие значения тока и напряжения, а
Внутри конденсатора протекает ток смещения сила которого численно равна:
vunivere.ru 6.10. Мощность в цепи синусоидального токаМгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток. Пусть мгновенные напряжение и ток определяются по формулам:
Тогда (6.23) Среднее значение мгновенной мощности за период Из треугольника сопротивлений , а . Получим еще одну формулу: . Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P. Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию. Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе , так как напряжение и ток в индуктивности или емкости различаются по фазе на 90o. В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q. Преобразуем выражение (6.23): где - мгновенная мощность в активном сопротивлении; - мгновенная мощность в реактивном элементе (в индуктивности или в емкости). Максимальное или амплитудное значение мощности p2 называется реактивной мощностью , где x - реактивное сопротивление (индуктивное или емкостное). Реактивная мощность, измеряемая в вольтамперах реактивных, расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания. Амплитудное значение суммарной мощности p = p1 + p2 называется полной мощностью. Полная мощность, измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока: , где z - полное сопротивление цепи. Полная мощность характеризует предельные возможности источника энергии. В электрической цепи можно использовать часть полной мощности , где - коэффициент мощности или "косинус "фи". Коэффициент мощности является одной из важнейших характеристик электротехнических устройств. Принимают специальные меры к увеличению коэффициента мощности. Возьмем треугольник сопротивлений и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 6.18). Из треугольника мощностей получим ряд формул: , , Рис.6.18 , . При анализе электрических цепей символическим методом используют выражение комплексной мощности, равное произведению комплексного напряжения на сопряженный комплекс тока. Для цепи, имеющей индуктивный характер (R-L цепи), где - комплекс напряжения; - комплекс тока; - сопряженный комплекс тока; - сдвиг по фазе между напряжением и током. , ток как в R-L цепи, напряжение опережает по фазе ток. Вещественной частью полной комплексной мощности является активная мощность. Мнимой частью комплексной мощности - реактивная мощность. Для цепи, имеющей емкостной характер (R-С цепи), . Ток опережает по фазе напряжение. . Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна. 6.11. Баланс мощностейДля схемы на рис. 6.19 запишем уравнение по второму закону Кирхгофа. Умножим левую и правую части уравнения на сопряженный комплекс тока где - результирующее реактивное сопротивление; I2- квадрат модуля тока. где - полная комплексная, активная и реактивная мощности источника питания. где - активная и реактивная мощности, потребляемые элементами схемы. Получим уравнение . (6.24) Рис. 6.19 Два комплексных числа равны, если равны по отдельности их вещественные и мнимые части, следовательно уравнение (6.24) распадается на два: . (6.25) Полученные равенства выражают законы сохранения активных и реактивных мощностей. 6.12. Согласованный режим работы электрической цепи. Согласование нагрузки с источникомВ схеме на рис. 6.20 - полное, активное и реактивное сопротивления источника ЭДС, - полное, активное и реактивное сопротивления нагрузки. Активная мощность может выделяться только в активных сопротивлениях цепи переменного тока. Активная мощность, выделяемая в нагрузке, . (6.26) Активная мощность, развиваемая генератором . Коэффициент полезного действия для данной схемы: . Рис. 6.20Из формулы (6.26) видно, что выделяемая в нагрузке мощность будет максимальной, когда знаменатель минимален. Последнее имеет место при , т.е. при . Это означает, что реактивные сопротивления источника и нагрузки должны быть одинаковы по модулю и иметь разнородный характер. При индуктивном характере реактивного сопротивления источника реактивное сопротивление нагрузки должно быть емкостным и наоборот. . (6.27) Установим условие, при котором от источника к нагрузке будет передаваться наибольшая мощность. . отсюда . От источника к нагрузке передается наибольшая мощность, когда . . (6.28) Величина наибольшей мощности . Режим передачи наибольшей мощности от источника к нагрузке называется согласованным режимом, а подбор сопротивлений согласно равенствам (6.28) - согласованием нагрузки с источником. В согласованном режиме . Половина мощности теряется внутри источника. Поэтому согласованный режим не используется в силовых энергетических цепях. Этот режим используют в информационных цепях, где мощности могут быть малыми, и решающими являются не соображения экономичности передачи сигнала, а максимальная мощность сигнала в нагрузке. nwpi-fsap.narod.ru | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|
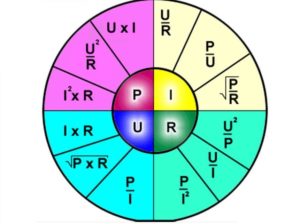Здравствуйте! Эту статью можно считать началом знакомства с электричеством. Напряжение, ток, сопротивление – это три главные величины, на которых построены основные законы электротехники и эти величины связаны между собой еще одной – мощностью. А чтобы было проще знакомиться с электротехникой, мы будем рассматривать мощность в цепи постоянного тока. Дело в том, что при расчетах в цепях переменного тока появляется довольно много условий. Впрочем, обо всём по порядку и вы сейчас сами с этим разберётесь.
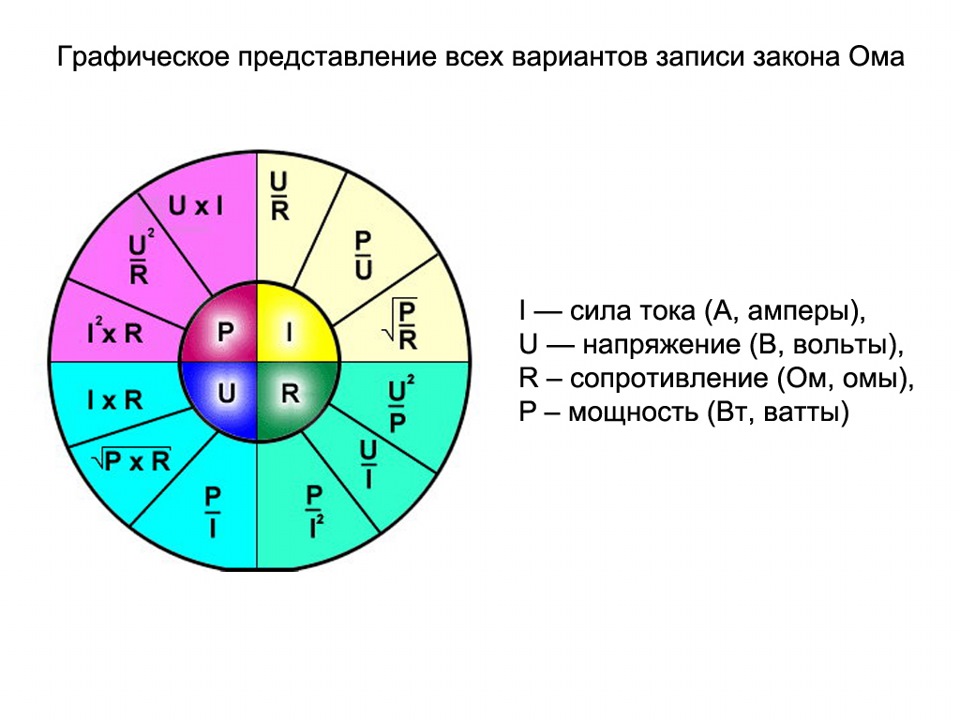
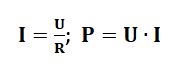
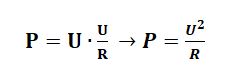
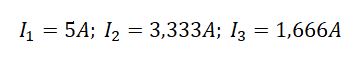
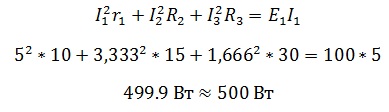
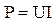(1). В цепи переменного тока мощность потребляемая нагрузкой имеет несколько значений.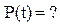
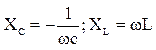
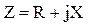, где j – минимальная единица. Комплексное сопротивление 
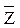, его модуль называется полным сопротивлением нагрузки 
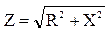. В общем случае на комплексной нагрузке ток и напряжение имеют фазовый сдвиг 
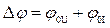, где 
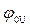и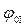 
начальные фаза тока и напряжение на нагрузке. Математически уравнение мгновенных напряжения и тока: 
; 
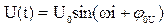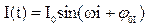, тогда мгновенное значение мощности найдется:
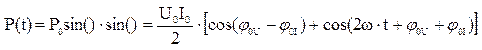(2)
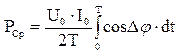
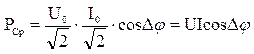(3)
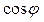- коэффициент мощности нагрузки, определяющий способность нагрузки поглощать эл. энергию и превращать её в тепловую. Ф. 3 определяет активную мощность поглощаемой нагрузки. Реактивная мощность, проходящая через нагрузку определяется по формуле 
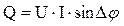(4).
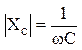Реактивная мощность нагрузкой не поглощается и возвращается в источник.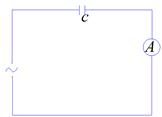 
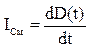, где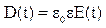 
. Кроме реактивной мощности вводится понятие полной мощности нагрузки 
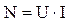(5), где U и I действительное значение тока и напряжения 
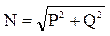(6). Комплексная мощность нагрузки 
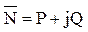(7). 
