Электрические цепи постоянного тока и методы их расчета (стр. 1 из 6). Как найти r0 электротехникаРешение задач по электротехнике (ТОЭ)Теоретические основы электротехники являются фундаментальной дисциплиной для всех электротехнических специальностей, а так же для некоторых неэлектротехнических (например, сварочное производство). На этой дисциплине основываются все спец. предметы электриков. Несмотря на большой объем дисциплины и кажущуюся сложность, она основана всего на нескольких законах. В этой статье я постараюсь рассмотреть решение основных задач, встречающихся в данном курсе. Законы Кирхгофа. Расчет цепей постоянного токаВ электротехнике существует два основных закона, на основании которых, теоретически можно решить все цепи. Первый закон Кирхгофа выглядит следующим образом.Сумма токов, входящих в узел, равна сумме токов, отходящих от узла.
Для данного рисунка имеем:I1 + I2 + I4 = I3 + I5. Второй закон Кирхгофа.Сумма напряжений вдоль замкнутого контура равна сумме ЭДС вдоль этого же контура. Для схемы на рисунке (стрелкой обозначим направление вдоль контура, которое будем считать условно положительным).
Начиная с узла, где сходятся токи I1, I3, I4 запишем все напряжения (по закону Ома):-I1⋅R1 — I1⋅R2 – в первой ветви (знак минус означает, что ток имеет направление противоположное выбранному направлению контура).I3⋅R3 – во второй ветви (знак «плюс», направление совпадает). Теперь запишем ЭДС:E2 — E3 (знак «минус» у E3, потому что направление ЭДС противоположно направлению контура). В соответствии с законом Кирхгофа напряжения равны ЭДС:-I1⋅R1 — I1⋅R2 + I3⋅R3 = E2 — E3. Как видите, все довольно просто. В большинстве случаев перед студентами стоит задача рассчитать величины токов во всех ветвях, зная величины ЭДС и резисторов. Для расчета сложной, разветвленной цепи постоянного тока, например этой, найденной на просторах интернета, воспользуемся следующими действиями.
Для начала задаемся условно положительными направлениями токов в ветвях (это значит, что ток может течь и в противоположном направлении, тогда он будет иметь отрицательное значение).
Составляем систему уравнений по второму закону Кирхгофа для каждого замкнутого контура так, чтобы охватить каждый неизвестный ток (в данной схеме имеем 3 таких контура). Направления контуров выбираем для удобства по часовой стрелке (хоть это и необязательно): По первому закону Кирхгофа составляем столько уравнений, чтоб охватить все неизвестные токи (в данной схеме для любых трех узлов): Итого, имеем систему из 6 уравнений. Чтобы решить такую систему можно воспользоваться программой MathCad. Решается она следующим образом:
Это скриншот программы. Знак «равно» в уравнения должен быть жирным (вкладка «булевы», CTRL + “=/+”).MathCad может решать системы любого порядка (например, схема имеет 10 независимых контуров). Но, во-первых, функция “Given” не работает с комплексными числами (об этом позже), во-вторых, не всегда есть под рукой компьютер или условие задачи поставлено так, что требуется решить схему другим методом. Данный метод решения задач называется методом непосредственного применения законов Кирхгофа. Большинство студентов старших курсов (уже прослушавших курс ТОЭ), инженеров-электриков, даже преподавателей и докторов наук могут решать схемы только этим методом, т.к. другие методы применяются крайне редко. Переменный ток.Переменный синусоидальный ток (или напряжение) задается уравнением:Здесь Im – амплитуда тока.ω – угловая частота, находится как ω = 2⋅π⋅f (обычно в условии задается либо f, либо ω)φ – фаза. Обычно в задачах условия задают либо в таком формате, либо в действующем значении. Амплитудное больше действующего всегда в √2 раз. Если в условии задано просто значение (например, E1 = 220 В), то это значит, что дано действующее значение. Если же в условии дано «250⋅sin(314t – 15°), В», то его нужно перевести в действующее комплексное значение. Про комплексные числа можно подробнее прочитать на нашем сайте. Для перевода величин к действующим необходимо: , Точечка над I означает, что это комплекс. Чтобы не путать с током, в электротехнике комплексная единица обозначается буквой «j». Для заданного напряжения имеем: В решении задач обычно оперируют действующими значениями. В переменном токе вводятся новые элементы:
Их сопротивления (реактивные сопротивления) находятся как:(сопротивление конденсатора — отрицательное) Например, имеем схему, она подключена на напряжение 200 В, имеющего частоту 100 Гц. Требуется найти ток. Параметры элементов заданы:
Чтоб найти ток, необходимо напряжение разделить на сопротивление (из закона Ома). Здесь основная задача – найти сопротивление. Комплексное сопротивление находится как:
Напряжение делим на сопротивление и получаем ток. Все эти действия удобно проводить в MathCad. Комплексная единица ставится «1i» или «1j». Если нет возможности, то:
Также, скажем пару слов о мощности. Мощность есть произведение тока и напряжения для цепей постоянного тока. Для цепей переменного тока вводится еще один параметр – угол сдвига фаз (вернее его косинус) между напряжением и током. Предположим, для предыдущей цепи нашли ток и напряжение (в комплексной форме). Также мощность можно найти и по другой формуле: В этой формуле — сопряженный комплекс тока. Сопряженный – значит, что его мнимая часть (та, что с j) меняет свой знак на противоположный (минус/плюс).Re – означает действительная часть (та, что без j). Это были формулы для активной (полезной) мощности. В цепях переменного тока существует так же и реактивная мощность (генерируется конденсаторами, потребляется – катушками). Реактивная мощность цепи: Im – мнимая часть комплексного числа (та, что с j). Зная реактивную и активную мощность можно подсчитать полную мощность цепи: Для упрощенного расчета цепей постоянного и переменного тока, содержащих большое число ветвей, пользуются одним из упрощенных методов анализа цепей. Рассмотрим подробнее метод контурных токов. Метод контурных токов (МКТ)Данный метод подходит для решения схем, содержащих больше узлов, чем независимых контуров (например, схема из раздела про постоянный ток). Принцип решения состоит в следующем:
Данный метод, как и другие (например, метод узловых потенциалов, эквивалентного генератора, наложения) пригоден для цепей как постоянного, так и переменного тока. При расчете цепей переменного тока сопротивления элементов приводятся к комплексной форме записи. Система уравнений решается также в комплексной форме. ЛитератураИз литературы можно порекомендовать Бессонова Л.А. «Теоретические основы электротехники: Электрические цепи». Также много информации в интернете на сайтах, посвященных электротехнике. Решение электротехники на заказИ помните, что наши решатели всегда готовы помочь Вам с ТОЭ. Подробнее. reshatel.org Показать содержимое по тегу: электротехника
В связи с широким развитием вычислительных устройств задача расчета и моделирования электрических схем заметно упростилась. Наиболее подходящим программным обеспечением для данных целей является продукт National instruments – Multisim (Electronic Workbench ). В данной статье рассмотрим простейшие примеры моделирования электрических схем с помощью Multisim. Итак, у нас имеется Multisim 12 это последняя версия на момент написания статьи. Откроем программу и создадим новый файл с помощью сочетания Ctrl+N. После создания файла перед нами открывается рабочая зона. По сути, рабочая зона Multisim – это поле для собирания требуемой схемы из имеющихся элементов, а их выбор, поверьте велик. Кстати вкратце о элементах. Все группы по умолчанию расположены на верхней панели. При нажатии на какую либо группу, перед вами открывается контекстное окно, в котором вы выбираете интересующий вас элемент. По умолчанию используется база элементов – Master Database. Компоненты содержащиеся в ней разделены на группы. Перечислим вкратце содержание групп. Sources содержит источники питания, заземление. Basic – резисторы, конденсаторы, катушки индуктивности и т.д. Diodes – содержит различные виды диодов. Transistors - содержит различные виды транзисторов. Analog - содержит все виды усилителей: операционные, дифференциальные, инвертирующие и т.д. TTL - содержит элементы транзисторно-транзисторная логики CMOS - содержит элементы КМОП-логики. MCU Module – управляющий модуль многопунктовой связи. Advanced_Peripherals – подключаемые внешние устройства. Misc Digital - различные цифровые устройства. Mixed - комбинированные компоненты Indicators - содержит измерительные приборы и др. С панелью моделирования тоже ничего сложного, как на любом воспроизводящем устройстве изображены кнопки пуска, паузы, останова. Остальные кнопки нужны для моделирования в пошаговом режиме. На панели приборов расположены различные измерительные приборы (сверху вниз) - мультиметр, функциональный генератор, ваттметр, осциллограф, плоттер Боде, частотомер, генератор слов, логический конвертер, логический анализатор, анализатор искажений, настольный мультиметр. Итак, бегло осмотрев функционал программы, перейдём к практике. Пример 1 Для начала соберём простенькую схему, для этого нам понадобиться источник постоянного тока (dc-power) и пара резисторов (resistor). Допустим нам необходимо определить ток в неразветвленной части, напряжение на первом резисторе и мощность на втором резисторе. Для этих целей нам понадобятся два мультиметра и ваттметр. Первый мультиметр переключим в режим амперметра, второй – вольтметра, оба на постоянное напряжение. Токовую обмотку ваттметра подключим во вторую ветвь последовательно, обмотку напряжения параллельно второму резистору. Есть одна особенность моделирования в Multisim – на схеме обязательно должно присутствовать заземление, поэтому один полюс источника мы заземлим. После того как схема собрана нажимаем на пуск моделирования и смотрим показания приборов. Проверим правильность показаний (на всякий случай=)) по закону Ома
Показания приборов оказались верными, переходим к следующему примеру. Пример 2 Соберём усилитель на биполярном транзисторе по схеме с общим эмиттером. В качестве источника входного сигнала используем функциональный генератор (function generator). В настройках ФГ выберем синусоидальный сигнал амплитудой 0,1 В, частотой 18,2 кГц. С помощью осциллографа (oscilloscope) снимем осциллограммы входного и выходного сигналов, для этого нам понадобится задействовать оба канала. Чтобы проверить правильность показаний осциллографа поставим на вход и на выход по мультиметру, переключив их предварительно в режим вольтметра. Запускаем схему и открываем двойным кликом каждый прибор. Показания вольтметров совпадают с показаниями осциллографа, если знать что вольтметр показывает действующее значение напряжения, для получения которого необходимо разделить амплитудное значение на корень из двух. Пример 3 С помощью логических элементов 2 И-НЕ соберём мультивибратор, создающий прямоугольные импульсы требуемой частоты. Чтобы измерить частоту импульсов воспользуемся частотомером (frequency counter), а проверим его показания с помощью осциллографа.
Итак, допустим, мы задались частотой 5 кГц, подобрали опытным путём требуемые значения конденсатора и резисторов. Запускаем схему и проверяем, что частотомер показывает приблизительно 5 кГц. На осциллограмме отмечаем период импульса, который в нашем случае равен 199,8 мкс. Тогда частота равна
Мы рассмотрели только малую часть всех возможных функций программы. В принципе, ПО Multisim будет полезен как студентам, для решения задач по электротехнике и электронике, так и преподавателям для научной деятельности и т.д. Надеемся данная статья оказалась для вас полезной. Спасибо за внимание! electroandi.ru Сборник задач по электротехнике с решениями. Учебное пособие
определяют ток I1 в первой ветви I1 = 1,2 −1,5I2 . 0,8 Ток I2 во второй ветви находят по значению токаI1 из уравнений для эдсE1 иE2: 1,8 = 1,6 1,2 −1,5I2 + 0,8I2 0,8 или 1,8 = 2,4 – 3I2 + 0,8I2, откуда I2 = 0,272 A. Величину тока I1 в первой ветви определяют по величине токаI2 из уравнения для эдсE1 1,8 = 1,6I1 + 0,8·0,27, откуда I1 = 0,99 А. Ток I3 в третьей ветви находят из уравнения для токов I3 =I1 +I2 = 0,99 + 0,27 = 1,26 A. 2.1.2)В электрической цепи постоянного тока (рис. 2.1.2) амперметр А показывает I5 = 5 А. Методом уравнений Кирхгофа рассчитать токиI1,I2,I3,I4 в ветвях цепи. Сопротивления резисторов: R1 = 1 Ом;R2 = 10 Ом;R3 = 10 Ом;
Величины эдс: E1 = 162 В;E2 = 50 В;E3 = 30 В. Внутренними сопротивлениями источников питания пренебречь. Решить задачу для случая, когда показание амперметра неизвестно. 1 2 3 Рис. 2.1.2 Решение. При заданном включении источников питания за положительные направления токов принимаем направления, указанные на схеме рис. 2.1.2. В схеме – три узла и пять ветвей, следовательно, необходимо определить пять неизвестных токов. В соответствии с этим составляют два уравнения по первому закону Кирхгофа и три – по второму закону Кирхгофа. Для узлов1 и2 цепи составляют уравнения для токов по первому закону Кирхгофа:
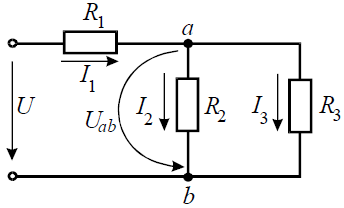
E1и E2 E1– E2= (R1+ R6+ R7)I1+ R2I2. Для контура с эдс E2 иE3 E2– E3= –R2I2+ R3I3+ (R4+ R8)I4. Для правого контура с амперметром А в ветви E3 =–(R4 +R8)I4 + (R5 +R9)I5. Ток в цепи резистора R4 определяют из последнего уравнения: 30 = –(4+ 6)I4 + (3 + 7) 5 =–10I4 + 50, откуда I4 = 2 A. Ток I3 в ветви резистораR3 находят из уравнения, составленного для узла2 цепи I3 =I4 +I5 = 7 А. Ток в ветви резистора R2 находят из уравнения, записанного для среднего замкнутого контура E2 –E3 =–10I2 + 10·7 + (4 + 6)·2, откуда I2 = 7 A. Ток в ветви с резисторами R1,R6,R7 находят из уравнения I1 =I2 +I3 = 14 A. Ток I1 можно также определить из уравнения E2– E3= –R2I2+ R3I3+ (R4+ R8)I4, откуда I1 = 14 A. Если ток в ветви резисторов R5 иR9 не задан, то искомые токи и их направления в других ветвях определяют, решая систему пяти уравнений, составленных по законам Кирхгофа. Положительные значения токов свидетельствуют о том, что действительные направления токов в соответствующих ветвях совпадают с условными направлениями. Задача 2.1.3)Методом уравнений Кирхгофа рассчитать токи I1, … ,I9 в ветвях электрической цепи, показанной на рис. 2.1.3. Электродвижущая сила и напряжения источников, сопротивления резисторов и положения выключателей для соответствующих вариантов задания указаны в табл. 2.1.1. Внутренними сопротивлениями источников пренебречь. Рис. 2.1.3 8При замене звезды сопротивлений эквивалентным треугольником сопротивлений сопротивления его сторон рассчитывают по формулам: R31= R3+ R1+ R3R1 ; R2 R12= R1+ R2+ R1R2 ; R3 R23= R2+ R3+ R2R3 . R1 Примеры решения задач 2.3.1)Найти эквивалентное сопротивление, токи в неразветвленной части и в отдельных ветвях цепи, показанной на рис. 2.3.5. К цепи приложено напряжение U. Рис. 2.3.5 Решение. СопротивленияR1,R2,R3 соединены параллельно. Их эквивалентная проводимостьGэ1 и сопротивлениеRэ1 равны:
В результате исходная схема (рис. 2.3.5) приводится к эквивалентной схеме (рис. 2.3.6, а), в которой сопротивленияR4 иRэ1 соединены последовательно. Их эквивалентное сопротивлениеRэ2 =R4 +Rэ1. На участкеcd (рис. 2.3.6,б) сопротивленияR5 иRэ2 соединены параллельно; их эквивалентное сопротивле-
сопротивления R6,Rэ3 иR7 соединены последовательно. Эквивалентное сопротивление исходной цепи Rэ= R6+ Rэ3+ R7. а) Рис. 2.3.6 Ток в неразветвленной части цепи I =U . Для расчета токов в ветвях по закону Ома для пассивного Rэ участка цепи определим напряжение на разветвленном участке цепи Ucd =IRэ1. Токи в ветвях:
Напряжение Uab = I4Rэ1. Токи в ветвях:
2.3.2)Задана мостовая схема (рис. 2.3.7, а). Сопротивления и эдс схемы известны. Рассчитать ток в сопротивленииR.
Рис. 2.3.7 Решение. Заменим треугольник сопротивленийR12,R23,R31 эквивалентной звездой сопротивленийR1,R2,R3, в результате получим схему со смешанным соединением сопротивлений (рис. 2.3.7,б). Эквивалентное сопротивление этой схемы Rэ = R + R1 + (R2+ R4)(R3+ R5) . R2+ R4+ R3+R5
= 12 Ом; R4 = 8 Ом;R5 = 1,5 Ом;E = 160 В;Rвт = 0,5 Ом. Определить токи во всех элементах схемы и кпд источника. Рис. 2.3.8 2.3.4)В схеме (рис. 2.3.8) ток I3 = 3 A. Определить эдс и мощность источника, приняв величины сопротивлений по условию задачи 2.3.3. 2.3.5)Задана цепь (рис. 2.3.9), в которой известны сопротивления R1 = 4 Ом;R2 = 4 Ом;R3 = 6 Ом;R4 =R5 = 120 Ом;R6 = 4 Ом и токI6 = 2 A. Определить токи остальных ветвей и эдсЕ. Рис. 2.3.9 2.3.6)Определить эквивалентное сопротивление относительно выводов а –b схем (рис. 2.3.10,а –е). Величины сопротивлений на схемах указаны в омах. 2.3.7)Определить напряжение Uab в схеме рис. 2.3.10,е.
Рис. 2.3.10 2.3.8) Как нужно соединить три сопротивления и выбрать их отношение, чтобы при питании от одного источника отношение напряжений на этих сопротивлениях было 1 : 2 : 3? 2.3.9) Как нужно соединить два сопротивления и выбрать их отношение, чтобы при питании от одного источника отношение токов в сопротивлениях было 1 : 3? 2.3.10) Преобразовать схему, показанную на рис. 2.3.11, в одноконтурную. 1 3 2 Рис. 2.3.11 2.3.11) Преобразовать эквивалентный источник эдс (рис. 2.3.12, а) в источник тока (рис. 2.3.12,б), определить параметры этого источника и потери в обоих источниках, еслиRн = 10 Ом;E = 60 В;Rвт = 2 Ом.
Rн = 4 Ом;Uab = 12 B, а мощность потерь 9 Вт. 2.3.14) Для измерения малых сопротивлений применяют двойной мост Томсона (рис. 2.3.13). Выведите условия равновесия моста, если сопротивления R1,R2,R3 иR4 подобраны так, чтоR2R3 =R4R1. x Рис. 2.3.13 2.3.15) За неимением одинаковых гальванических элементов пришлось включить параллельно два гальванических элемента с эдс E1 иE2 с внутренними сопротивлениямиRвт1 иRвт2 соответственно. Во внешней цепи, сопротивление которойR, протекает токI. Найти эдсE и внутреннее сопротивлениеRвт гальванического элемента, который дает во внешнюю цепь такой же ток при любом сопротивленииR, и показать, чтоE всегда меньше наибольшей из эдсE1 иE2. 2.3.16) В цепи, схема которой приведена на рис. 2.3.14, известны все сопротивления и ток I4 через резисторR4. Найти эдсE источника. Внутренним сопротивлением источника пренебречь. Рис. 2.3.14 2.3.17) В цепи постоянного тока (рис. 2.3.15) E = 10 В;R1 = 5 Ом;R2 =R3 = 1 Ом;R4 =R5 = 3 Ом. Найти токи в каждой ветви. Внутренним сопротивлением источника пренебречь.
рис. 2.3.16, известны сопротивления R1,R2 иR3, токI в источнике эдсE и разность потенциаловU21 между точками2 и1. Найти сопротивление резистораR4. 1 2 Рис. 2.3.16 2.3.19) Сопротивления ветвей цепи (рис. 2.3.17) R1 =R2 =R3 = 60 Ом;R4 =R5 =R6 = 30 Ом, внутрен-
studfiles.net Расчет электрических цепей постоянного тока методом эквивалентных преобразованийГлавная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований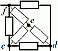 Расчет электрических цепей постоянного тока методом эквивалентных преобразований Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа. На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем. Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы. Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи. В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы. Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
Рис. 1 Решение Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
Решение Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
n – количество параллельно соединенных сопротивлений.
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
Рис. 3 Решение Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
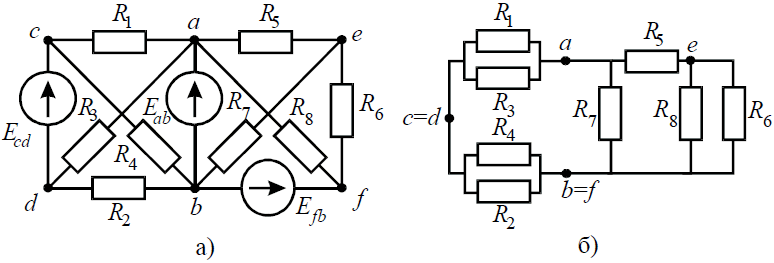
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом. Решение Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4 Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
Рис. 5 Решение Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
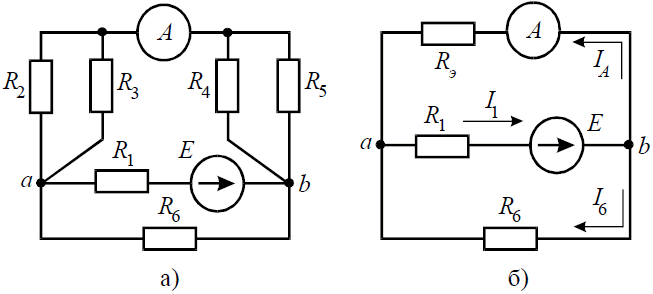
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6 Решение Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б). Величина эквивалентного сопротивления:
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
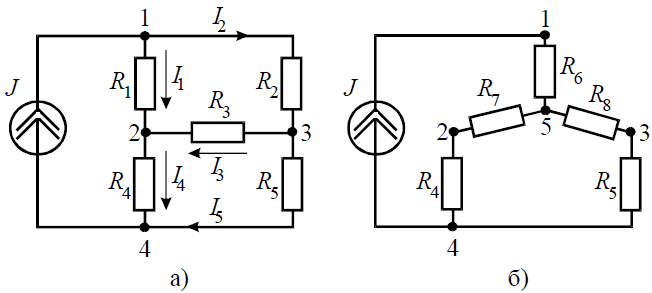
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Рис. 7 Решение Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований Расчет электрических цепей постоянного тока методом эквивалентных преобразований
02.09.2011, 211620 просмотров. rgr-toe.ru 10 формул по физикеДоброго дня уважаемые радиолюбители!Приветствую вас на сайте “Радиолюбитель“ Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем. Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить. В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки. Соотношения закона ОмаЗакон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:
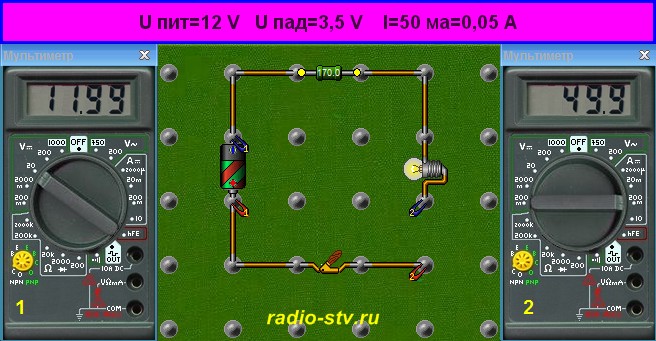
В этой таблице используются следующие общепринятые обозначения физических величин: U — напряжение (В), I — ток (А), Р — мощность (Вт), R — сопротивление (Ом), Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца. А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен: I = U / R Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.
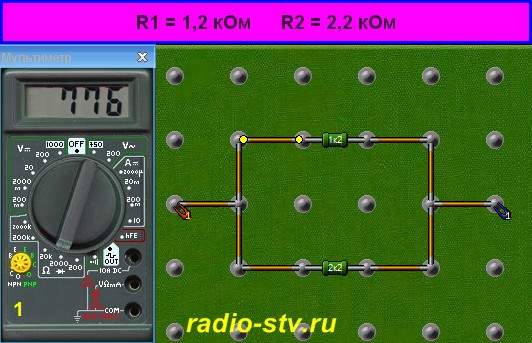
Что же в этой формуле есть что? Рассмотрим переменные подробнее. > U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В. > I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А. > R: искомое сопротивление токоограничивающего резистора, в омах. В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R: R = U/I = 8,5 В / 0,050 А= 170 Ом Расчёты сопротивленияРассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее. Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин. > Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно. > Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи. Расчет сопротивления последовательных резисторовФормула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления: Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов) В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина. Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.
Расчет сопротивления параллельных резисторовВсе немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид: R общ = R1 * R2 / (R1 + R2) где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим 776,47 = 2640000 / 3400
Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула: Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина. Расчёты ёмкостиФормулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи. Расчет емкости параллельных конденсаторовЕсли нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы: Собщ = CI + С2 + СЗ + … В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина. Расчет емкости последовательных конденсаторовДля вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула: Собщ = С1 * С2 /( С1+С2) где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи Расчет емкости трех и более последовательно соединенных конденсаторовВ схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи: И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина. Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники. Расчёт энергетических уравненийНаиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова: ватт-часы = Р х Т В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600. Расчёт постоянной ёмкости RC-цепочкиВ электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка). Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов. Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами. T = RC В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах. Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс. Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:
Расчёты частоты и длины волныЧастота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах. Расчет частоты сигналаПредположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны: Частота = 300000 / длина волны Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах. Расчет длины волны сигналаТу же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота: Длина волны = 300000 / Частота Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах. Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим: 6000 миллиметров = 300000 / 50 МГц Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно! radio-stv.ru Сборник задач по электротехнике с решениями. Учебное пособиеРис. 2.3.17
R1 =R2 = 0,5 Ом;R3 = 6 Ом;R4 = 6 Ом;R5 =R6 = 1 Ом;R7 = 2 Ом, а напряжение на входеU = 120 В. 2.3.22) В схеме цепи (рис. 2.3.20) определить напряжениеUab. Значения эдс и сопротивлений указа- ны соответственно в В и Ом. Рис. 2.3.19 a
cd Рис. 2.3.21 2.3.24) Определить входное сопротивление схемы Rab (рис. 2.3.22) относительно точекa иb, еслиJ5 иJ6 – источники тока. Рис. 2.3.22 2.3.25) В цепи (рис. 2.3.23) сопротивления резисторов даны в омах. Определить входное сопротивление схемы относительно точек a иb. Рис. 2.3.23 2.4 МЕТОД УЗЛОВОГО НАПРЯЖЕНИЯ Метод узлового напряжения целесообразно использовать для расчета электрических цепей, содержащих несколько параллельных ветвей, присоединенных к паре узлов. Преимущество этого метода перед другими возрастает с увеличением числа параллельных ветвей электрических цепей, при этом определяется узловое напряжение, что позволяет достаточно просто определять токи в параллельных ветвях и другие величины, характеризующие подобные электрические цепи. Узловое напряжение между двумя точками разветвлений (узлами) определяют в соответствии с выражением
k =1 При расчете электрических цепей по методу узлового напряжения задают условное положительное направление указанного напряжения, рассчитывая его по соответствующей формуле. При этом определяют проводимости всех ветвей, выбирая условно положительные направления токов в ветвях. При определении токов в параллельных ветвях для соответствующих замкнутых контуров выбирают направления обхода контура и составляют уравнение по второму закону Кирхгофа. При этом эдс, напряжения и токи источников тока принимаются положительными, если они направлены по направлению обхода контура, и отрицательными, если они направлены против направления обхода контура. При отсутствии в цепи источников тока (рис. 2.4.1, а) выражение для определения узлового напряжения принимает вид
При заданном условном положительном направлении напряжения U12, действующего между узлами1 и2 (рис. 2.4.1,б), эдс в замкнутом контуре, образованном соответствующей ветвью и замыкающим его напряжениемU12, считается положительной, если совпадает с направлением обхода контура, и отрицательной, если не совпадает. Знаки в расчетной формуле не зависят от направления токов в ветвях электрической цепи, поэтому выражение для напряжений между узлами1 и2 цепи записывается в виде
Для расчетов тока в ветвях электрической цепи составляют замкнутый контур, состоящий из рассматриваемой ветви цепи, замыкаемой напряжением U12 между узлами с учетом действительного его направления. Расчетная схема ветви с резисторомR1 и эдсE1 приведена на рис. 2.4.1,б. Задавшись условным положительным направлением обхода полученного контура, например, по часовой стрелке (пунктирная линия на рис. 2.4.1,б), по второму закону Кирхгофа с учетом знаков составляется уравнение E1= I1R1+ U12, из которого определяется величина тока I1 в данной ветви цепи. Аналогичным образом определяются токи в других ветвях электрической цепи. Примеры решения задач 2.4.1)Для электрической цепи постоянного тока (рис. 2.4.2) определить при какой величине эдс E3 токI3 в ветви с резисторомR3 уменьшится в три раза по сравнению с его первоначальным значением. Электродвижущая сила источников питания:E1 = 100 B;E2 = 120 B;E3 = 150 B. 1 2 Рис. 2.4.2 Сопротивления резисторов: R1 = 20 Ом;R3 = 100 Ом;R4 = 60 Ом. Внутренними сопротивлениями источников питания пренебречь. Решение. По второму закону Кирхгофа напряжение, действующее между двумя узлами1 и2 электрической цепиU12 =E2 = 120 В. ТокI3 в ветви резистораR3 для первоначальных условий определяется из выражения, записанного для ветви по второму закону Кирхгофа: E3= U12+ I3R3, откуда I3 = E3 −U12 = 150−120= 0,3 A. R3 100 Электродвижущая сила E3′ , при которой токI3′ в цепи резистораR3 уменьшается в три раза, определяется из выражения для эдсE3 E3′ =U12 +I3′ R3 = 120 – 100I3′ . Из условия I3′ =I33 = 0,1 A находим E3′ = 120 + 100 0,1 = 130 B. 2.4.2)Два источника постоянного тока с эдс E1 =E2 = 115 B и внутренними сопротивлениямиR01 = 0,2 Ом иR02 = 0,4 Ом включены параллельно в нагрузкуRн = 5 Ом (рис. 2.4.3). Определить токиI,I1,I2 в ветвях цепи и составить баланс мощностей. 1 2 Рис. 2.4.3 Решение. Проводимости ветвей электрической цепи:
Gн =1 =1 =0,2 См; Rн5
Узловое напряжение, действующее между узлами 1 и2 цепи:
Принимаем положительные направления токов в ветвях в соответствии с рис. 2.4.3. По второму закону Кирхгофа для ветви генератора с эдс E1 можно записать уравнение электрического равновесия: U12+ I1R01= E1, откуда I1 =E1 −U12 = (E1 –U12)G1 = (115 – 112)·5 = 5 A. R01 Задачи 2.4.3)На рис. 2.4.4 приведена мостовая электрическая схема соединения сопротивлений R1…R5. Определить величину и направление токаI5 в диагонали моста с резисторомR5, если напряжение источни-
2 Рис. 2.4.4 1 2 РИС. 2.4.5 2.4.6)Определить токи в ветвях электрической цепи постоянного тока (рис. 2.4.6, а). Электродвижущая сила источников питанияE1 иE2; внутренние сопротивленияR01 иR02; сопротивления резисторовR1…R7, а также схема включения резисторов на участке2 –3 (ограниченная пунктиром на рис. 2.4.6,б –е) для соответствующих вариантов задания приведены в табл. 2.4.1. Задачу решить методом узлового напряжения. 2.5 МЕТОД НАЛОЖЕНИЯ ТОКОВ Метод наложения токов (метод суперпозиции) применяется для расчета сложных электрических цепей постоянного тока с несколькими источниками энергии. Наиболее целесообразно применять его при небольшом числе источников. По сравнению с другими методами он имеет преимущества в тех случаях, когда не требуется полный расчет цепи, а можно ограничиться, например, определением токов только в некоторых ветвях электрической цепи. 1 02 01 б) а) в) г) д)
е) Рис. 2.4.6 В методе наложения электрическая цепь с несколькими источниками эдс и напряжений заменяется расчетными электрическими цепями с одним источником. Число расчетных цепей равно числу источников, действующих в электрической цепи. Источники питания, кроме рассматриваемого, из цепи удаляют, оставляя в цепи только их внутренние сопротивления. В результате расчета каждой преобразованной цепи определяются частичные токи от действия данного источника. Значение действительных токов ветвей определяется алгебраическим суммированием частичных токов в этих ветвях. Применительно к исходной электрической цепи (рис. 2.5.1, а), на которой предва- рительно нанесены положительные направления токов в ветвях, приведены расчетные электрические цепи (рис. 2.5.2, б –в) для частичных токов от действия эдс
01 02 в) Рис. 2.5.1 E1 иE2. При расчете этих цепей определяются частичные токи во всех ветвях. С учетом направления частичных токов и токов в ветвях исходной электрической цепи определяют действительные токи в ветвях рассматриваемой цепи путем наложения (алгебраического суммирования) частичных токов в ветвях:
(рис. 2.5.2, а), а также диапазон изменения сопротивления резистораR для зарядки аккумуляторной батареи до эдсE2 = 16 B в конце зарядки при неизменном токе нагрузки цепей. Сопротивление резистораR = 4 Ом; эдс генератораE1 = 36 B; внутреннее сопротивлениеR01 = 0,3 Ом. Электродвижущая сила ак-
01 02
Ток в электрической цепи при наличии обоих источников питания I = I ′− I ′′ = 8,35 – 2,78 = 5,57 A. Сопротивление электрической цепи в начале зарядки аккумуляторной батареи при токе I = 5,57 A Rн′ =E1 −I E2 =365,−5712 =4,31 Ом. Сопротивление нагрузочного резистора в начале зарядки батареи R′ = Rн′ −(R01 + R02 ) = 4,31 – (0,3 + 0,01) = 4 Ом. Сопротивление электрической цепи в конце зарядки аккумуляторной батареи при токе I = 5,57 A Rн′′ =E1 −I E2 =365,−5716 =3,59 Ом. Сопротивление нагрузочного резистора в конце зарядки аккумуляторной батареи при токе I = 5,57 A R′′ = Rн′′ −(R01 + R02 ) = 3,59 – (0,3 + 0,01) = 3,28 Ом. Диапазон изменения сопротивления нагрузочного резистора при заданных условиях KR =RR′′′ =34,,2831 =1,31. Задачи studfiles.net Электрические цепи постоянного тока и методы их расчетаЭлектрические цепи постоянного тока и методы их расчета 1.1. Электрическая цепь и ее элементы В электротехнике рассматривается устройство и принцип действия основных электротехнических устройств, используемых в быту и промышленности. Чтобы электротехническое устройство работало, должна быть создана электрическая цепь, задача которой передать электрическую энергию этому устройству и обеспечить ему требуемый режим работы. Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении. Для анализа и расчета электрическая цепь графически представляется в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения. Электрическая схема простейшей электрической цепи, обеспечивающей работу осветительной аппаратуры, представлена на рис. 1.1.  Рис. 1.1 Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы: 1) Источники электрической энергии (питания). Общим свойством всех источников питания является преобразование какого-либо вида энергии в электрическую. Источники, в которых происходит преобразование неэлектрической энергии в электрическую, называются первичными источниками. Вторичные источники – это такие источники, у которых и на входе, и на выходе – электрическая энергия (например, выпрямительные устройства). 2) Потребители электрической энергии. Общим свойством всех потребителей является преобразование электроэнергии в другие виды энергии (например, нагревательный прибор). Иногда потребители называют нагрузкой. 3) Вспомогательные элементы цепи: соединительные провода, коммутационная аппаратура, аппаратура защиты, измерительные приборы и т.д., без которых реальная цепь не работает. Все элементы цепи охвачены одним электромагнитным процессом. В электрической схеме на рис. 1.1 электрическая энергия от источника ЭДС E, обладающего внутренним сопротивлением r0 , с помощью вспомогательных элементов цепи передаются через регулировочный реостат R к потребителям (нагрузке): электрическим лампочкам EL1 и EL2 . 1.2. Основные понятия и определения для электрической цепи Для расчета и анализа реальная электрическая цепь представляется графически в виде расчетной электрической схемы (схемы замещения). В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают. Источник питания показывается как источник ЭДС E с внутренним сопротивлением r0 , реальные потребители электрической энергии постоянного тока заменяются их электрическими параметрами: активными сопротивлениями R1 , R2 , …, Rn . С помощью сопротивления R учитывают способность реального элемента цепи необратимо преобразовывать электроэнергию в другие виды, например, тепловую или лучистую. При этих условиях схема на рис. 1.1 может быть представлена в виде расчетной электрической схемы (рис. 1.2), в которой есть источник питания с ЭДС E и внутренним сопротивлением r0 , а потребители электрической энергии: регулировочный реостат R, электрические лампочки EL1 и EL2 заменены активными сопротивлениями R, R1 и R2 .  Рис. 1.2 Источник ЭДС на электрической схеме (рис. 1.2) может быть заменен источником напряжения U, причем условное положительное направление напряжения U источника задается противоположным направлению ЭДС. При расчете в схеме электрической цепи выделяют несколько основных элементов. Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов. Схема на рис. 1.2 имеет три ветви: ветвь bma, в которую включены элементы r0 , E, R и в которой возникает ток I; ветвь ab с элементом R1 и током I1 ; ветвь anb с элементом R2 и током I2 . Узел электрической цепи (схемы) – место соединения трех и более ветвей. В схеме на рис. 1.2 – два узла a и b. Ветви, присоединенные к одной паре узлов, называют параллельными. Сопротивления R1 и R2 (рис. 1.2) находятся в параллельных ветвях. Контур – любой замкнутый путь, проходящий по нескольким ветвям. В схеме на рис. 1.2 можно выделить три контура: I – bmab; II – anba; III – manbm, на схеме стрелкой показывают направление обхода контура. Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений между узлами и на зажимах элементов цепи необходимо задать для правильной записи уравнений, описывающих процессы в электрической цепи или ее элементах. На схеме (рис. 1.2) стрелками укажем положительные направления ЭДС, напряжений и токов: а) для ЭДС источников – произвольно, но при этом следует учитывать, что полюс (зажим источника), к которому направлена стрелка, имеет более высокий потенциал по отношению к другому полюсу; б) для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно; в) для напряжений – совпадающими с направлением тока в ветви или элемента цепи. Все электрические цепи делятся на линейные и нелинейные. Элемент электрической цепи, параметры которого (сопротивление и др.) не зависят от тока в нем, называют линейным, например электропечь. Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке. Следовательно, в линейной электрической цепи все элементы – линейные, а нелинейной называют электрическую цепь, содержащую хотя бы один нелинейный элемент. 1.3. Основные законы цепей постоянного тока Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. На основе этих законов устанавливается взаимосвязь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами элементов, входящих в состав этой цепи. Закон Ома для участка цепи Соотношение между током I, напряжением UR и сопротивлением R участка аb электрической цепи (рис. 1.3) выражается законом Ома  Рис. 1.3 Рис. 1.3 (1.1)  или UR = RI. или UR = RI. В этом случае UR = RI – называют напряжением или падением напряжения на резисторе R, а  – током в резисторе R. – током в резисторе R. При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью:  . . В этом случае закон Ома для участка цепи запишется в виде: I = Uq. Закон Ома для всей цепи Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r0 (рис. 1.3), током I электрической цепи и общим эквивалентным сопротивлением RЭ = r0 + R всей цепи: (1.2)  . . Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии. Первый закон Кирхгофа В любом узле электрической цепи алгебраическая сумма токов равна нулю (1.3)  , , где m – число ветвей подключенных к узлу. При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 1.2) I - I1 - I2 = 0. Второй закон Кирхгофа В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках (1.4)  , , где n – число источников ЭДС в контуре;m – число элементов с сопротивлением Rк в контуре;Uк = Rк Iк – напряжение или падение напряжения на к-м элементе контура. Для схемы (рис. 1.2) запишем уравнение по второму закону Кирхгофа: E = UR + U1 . Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контру, включая источники ЭДС равна нулю (1.5)  . . При записи уравнений по второму закону Кирхгофа необходимо: 1) задать условные положительные направления ЭДС, токов и напряжений; 2) выбрать направление обхода контура, для которого записывается уравнение; 3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны. mirznanii.com | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|












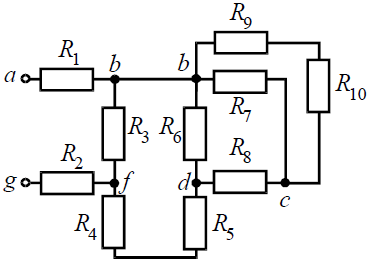
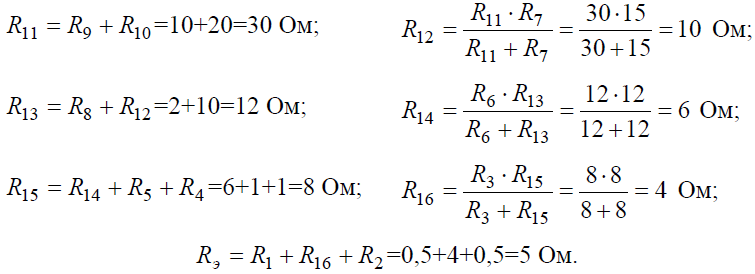
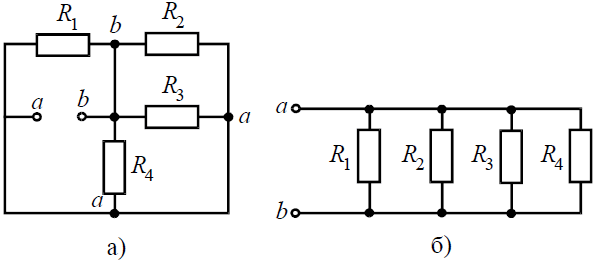 Рис. 2
Рис. 2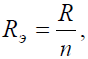 где R – величина сопротивления, Ом;
где R – величина сопротивления, Ом;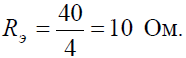
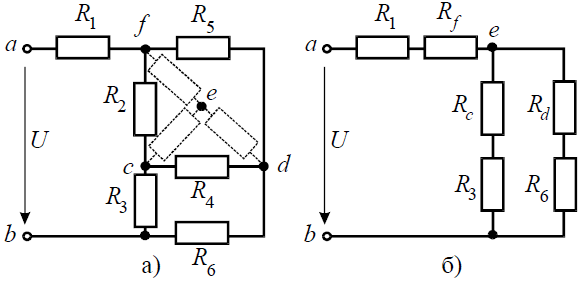
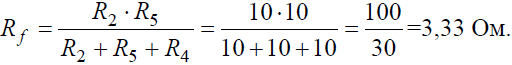 По условию задачи величины всех сопротивлений равны, а значит:
По условию задачи величины всех сопротивлений равны, а значит: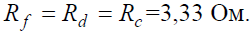 На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно: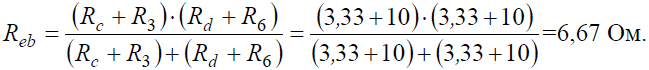
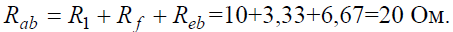
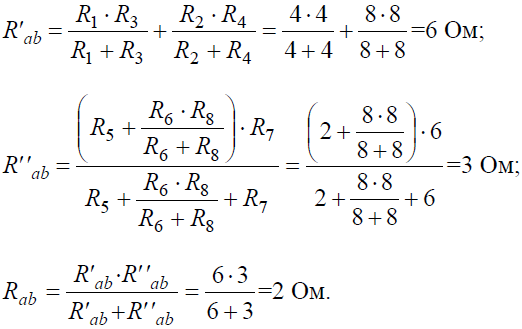
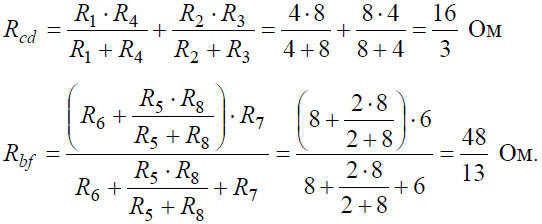
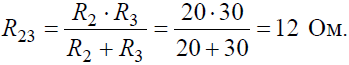
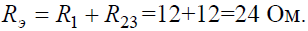
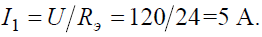
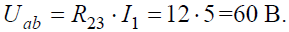
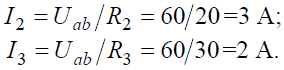
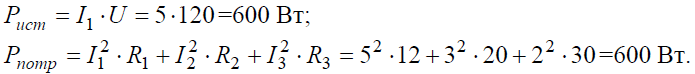
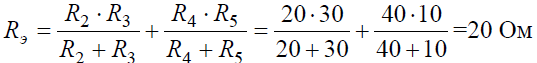
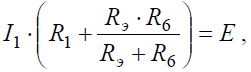
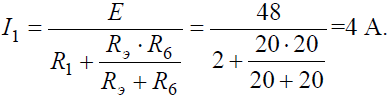
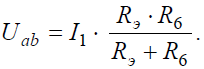
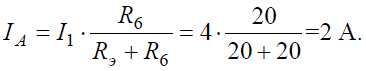
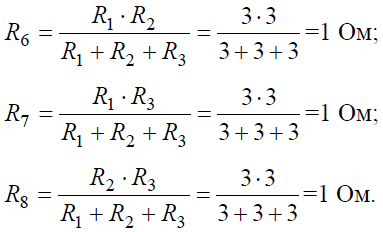
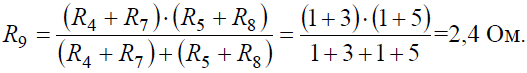
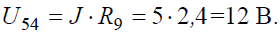

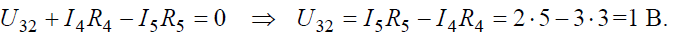
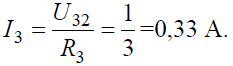
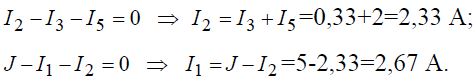
 Метод эквивалентных преобразований
Метод эквивалентных преобразований