Какое число называют ФИ? Фи в чем измеряетсяФи (число) Википедия1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362 Первая тысяча знаков значения Φ[1].Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }[2], φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}Отсюда следует, что φ=Φ−1{\displaystyle \varphi =\Phi -1}.Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %. Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины. Иллюстрация к определениюЧисло Φ{\displaystyle \Phi } называется также золотым числом. Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства[3][4][5]. ИсторияВ дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника. Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа[6]. Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке[7] или относят появление этого термина к XVI веку[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам[10][11], хотя некоторые авторы утверждают обратное[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.[16] Математические свойства1Φ=φ=tg(arctg(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}
Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 931 день] Золотое сечение в наукеОбщее сопротивление этой бесконечной цепи равно Фr.Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r. Отношение амплитуд колебаний и частот ~ Ф.Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок). Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии. Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.70 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н20)21, который представляет из себя ион Н30+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды[23]. Золотое сечение и гармония в искусствеЗолотое сечение и зрительные центрыНекоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:
Примеры сознательного использованияНачиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 524 дня]. Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза. Золотое сечение в биологии и медицинеЗолотое сечение в природеЖивые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов[25][неавторитетный источник? 373 дня] и др. См. такжеПримечания
Литература
Ссылкиwikiredia.ru Число ФИ: значениеЧисло ФИ или латинскими буквами PHI – это число, которое обозначает все красивое во Вселенной. Что же это за необычное число, и какие другие названия у него существуют?  Число Фи обозначает все красивое во Вселенной Почему это число называют золотым сечением?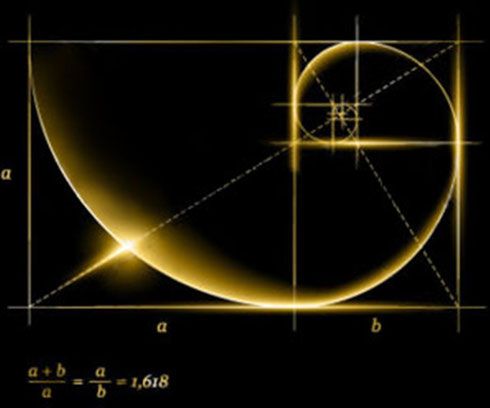 Это число получил исследователь Фибоначчи В древней Греции был один скульптор Фидий, который обладал удивительным талантом. Все восхищались его скульптурами и пытались разгадать, как этому творцу удается каждый раз делать настоящее произведение искусства. Позже стало известно, что в каждой своей скульптуре Фидий придерживается определенного числа в пропорциях. Затем оказалось, что не только этот творец использовал в своем искусстве это необыкновенное число. Оно было обнаружено в произведениях искусства художника Рафаэля, русского художника Шишкина, число гнездилось в музыкальных произведениях Бетховена, Шопена и Чайковского. Знаменитая «Джаконда» Леонардо Да Винчи тоже содержит в себе это число. Его еще называют золотым сечением. ЧИСЛА ФИБОНАЧЧИ УДИВИТЕЛЬНАЯ ЗАКОНОМЕРНОСТЬ [Число ФИ и Золотое сечение] Тайна числа 1.618034 - самое ВАЖНОЕ число в мире ЗОЛОТОЕ СЕЧЕНИЕ По математическим меркам число ФИ равно 1.618, его получил исследователь Фибоначчи. Этот ученый в результате своих исследований пришел к тому, что все числа имеют четкую последовательность. Каждый следующий член, начиная с третьего числа, несет в себе сумму двух прошлых членов. А частное двух соседних чисел представляет собой максимально приближено к числу 1.618, то есть к тому самому числу ФИ. Золотое сечение и пропорции человеческого тела Человеческое тело сотворено по принципу золотого сечения Наверное, все видели знаменитую картину Леонардо Да Винчи, где расчерчено человеческое тело. Именно при помощи этой знаменитой схеме Леонардо доказал, что человеческое тело сотворено по принципу золотого сечения. Пропорции тела человека всегда дают то самое число красоты ФИ. При желании такую теорию можно легко проверить на практике. Нужно измерить при помощи сантиметра длину от плеча до кончика самого длинного пальца, а потом поделить его на длину от локтя до кончика того же самого пальчика. Удивительно, но в результате вы получите как раз 1.618! То самое число красоты. Это не единственный пример. Измерьте расстояние от верхней части бедра, поделите его на длину от колена до пола, вы получите такое же значение. Таким образом, легко доказать, человек полностью состоит из божественной пропорции. Кроме того на теле человека легко можно обнаружить признак того самого золотого сечения. Это наш пупок. Интересно отметить, что замеры тела мужчин чуть больше приближены к заветному числу. Это примерно 1.625. Женские же пропорции больше подходят под значение 1.6. Секреты пирамид На принципе числа Фи построены пирамиды в Гизе На протяжении многих лет люди пытались открыть загадку Пирамиды в Гизе. Но на этот раз пирамида интересовала человечество не в качестве склепа, а как уникальная комбинация числовых значений. Эту пирамиду возвел мастер, который обладает удивительной изобретательностью, он не пожалел труда и времени для этого произведения. На ее сотворение были пущены лучшие архитекторы, которых удалось найти. Долго современные ученые недоумевали как древним египтянам, у которых не было письменности, удалось придумать такой сложный геометро-математический ключ. После длительных просчетов оказалось, что и в этом случае не обошлось без золотого сечения и числа ФИ. Как раз на этом принципе и основана эта пирамида. Некоторые современные ученые считают, что посредством этого произведения древние египтяне пытались передать своим современникам секрет природной красоты и гармонии. Не исключительно в Гизе существуют пирамиды, которые выстроены, пирамиды, которые расположены в Мексике, тоже выстроены таким образом. Именно поэтому современные исследователи приходят к выводу, что пирамиды на этих территориях были построены народом, который имеет общие корни. Число ФИ в космосе В астрономии тоже присутствует число Фи Астроном из Германии Тициус в XVIII столетии заметил, что ряд числовых значений Фибоначчи присутствует и в расстоянии между планетами всей солнечной системы. В этом не было бы ничего удивительного, если бы такая закономерность не шла в противостоянии с одним законом. Дело в том, что между Марсом и Юпитером планеты нет, так раньше думали астрономы. Однако после выведения этой закономерности, они тщательно исследовали эту область галактики и обнаружили там ряд астероидов. К сожалению, такое важное открытие произошло, когда тот самый Тициус уже ушел из жизни. Теперь в астрономии при помощи числовых соотношений Фибоначчи представляют строение Галактик. Такой факт свидетельствует о независимости данных числовых соотношений от условий проявления, тем самым доказывается их универсальность. Примеры числа ФИ из природы Существуют интересные примеры числа ФИ из самой природы Вот интересные примеры числа ФИ из самой природы:
Исходя из всех этих примеров, их на самом деле гораздо больше ученые делают вывод, что в мире растений и мире животных присутствует симметрия в отношении роста и движения. Золотое сечение проявлено здесь перпендикулярно к направлению роста. Золотое сечение и теория Хаоса В каждом природном явлении присутствует свое золотое соотношение чисел Одни ученые заметили, что все в мире происходит хаотично. А другие подвели итог, что даже в хаосе, которому подвержен весь мир, можно найти свои конкретные закономерности. Эти самые закономерности тоже выражены в числовых значениях Фибоначчи. В каждом природном явлении присутствует свое золотое соотношение чисел. В этом смысле природа не может соревноваться с сухой и скучной геометрией. Геометрия при всей своей точности и конструктивности не способна описать форму облака, дерева или горы. Облако не может быть представлено сферой, гора конусом, берег моря не может найти свое выражение в геометрической окружности. Кора дерева не может быть выражена этой наукой, потому что она не гладкая, а молния никогда не будет двигаться по прямой. Природные явления представляют собой не только более высокую степень, а совершенно новый уровень сложности. В природе представлены наборы масштабов, разные длины объектов, поэтому они способны закрывать неисчислимое количество потребностей. Такой набор масштабов и измерений несет название фрактал. Именно при помощи фракталов ученые не оставляют попытки сделать описание объектов, которые не доступны линейной геометрии. Это фрактальная геометрия. Каждый человек тоже представляет собой фрактал. А еще интересно то, что число ФИ имеет бесконечную природу, это означает, что мы бесконечно можем делать новые открытия во Вселенной и в себе самом. privorogi.ru Все главные формулы по физике - Физика - Теория, тесты, формулы и задачиОглавление:
КинематикаК оглавлению... Путь при равномерном движении: Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей): Средняя скорость пути: Средняя скорость перемещения: Определение ускорения при равноускоренном движении: Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении: Средняя скорость при равноускоренном движении: Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам: Координата при равноускоренном движении изменяется по закону: Проекция скорости при равноускоренном движении изменяется по такому закону: Скорость, с которой упадет тело падающее с высоты h без начальной скорости: Время падения тела с высоты h без начальной скорости: Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку): Формула для тормозного пути тела: Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле: Дальность полета тела при горизонтальном броске с высоты H: Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту: Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня): Время подъема до максимальной высоты при броске под углом к горизонту: Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю): Определение периода вращения при равномерном движении по окружности: Определение частоты вращения при равномерном движении по окружности: Связь периода и частоты: Линейная скорость при равномерном движении по окружности может быть найдена по формулам: Угловая скорость вращения при равномерном движении по окружности: Связь линейной и скорости и угловой скорости выражается формулой: Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии): Центростремительное ускорение находится по одной из формул:
ДинамикаК оглавлению... Второй закон Ньютона: Здесь: F - равнодействующая сила, которая равна сумме всех сил действующих на тело: Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике): Третий закон Ньютона (сила действия равна силе противодействия): Сила упругости: Общий коэффициент жесткости параллельно соединённых пружин: Общий коэффициент жесткости последовательно соединённых пружин: Сила трения скольжения (или максимальное значение силы трения покоя): Закон всемирного тяготения: Если рассмотреть тело на поверхности планеты и ввести следующее обозначение: Где: g - ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести: Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой: Скорость спутника на круговой орбите: Первая космическая скорость: Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
СтатикаК оглавлению... Момент силы определяется с помощью следующей формулы: Условие при котором тело не будет вращаться: Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
ГидростатикаК оглавлению... Определение давления задаётся следующей формулой: Давление, которое создает столб жидкости находится по формуле: Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид: Идеальный гидравлический пресс: Любой гидравлический пресс: КПД для неидеального гидравлического пресса: Сила Архимеда (выталкивающая сила, V - объем погруженной части тела):
ИмпульсК оглавлению... Импульс тела находится по следующей формуле: Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная): Общий импульс системы тел (важно то, что сумма векторная): Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы: Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется: Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергияК оглавлению... Механическая работа рассчитывается по следующей формуле: Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность): Мгновенная механическая мощность: Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы: Формула для кинетической энергии: Потенциальная энергия тела поднятого на высоту: Потенциальная энергия растянутой (или сжатой) пружины: Полная механическая энергия: Связь полной механической энергии тела или системы тел и работы внешних сил: Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физикаК оглавлению... Химическое количество вещества находится по одной из формул: Масса одной молекулы вещества может быть найдена по следующей формуле: Связь массы, плотности и объёма: Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа: Определение концентрации задаётся следующей формулой: Для средней квадратичной скорости молекул имеется две формулы: Средняя кинетическая энергия поступательного движения одной молекулы: Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом: Следствия из основного уравнения МКТ: Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева): Газовые законы. Закон Бойля-Мариотта: Закон Гей-Люссака: Закон Шарля: Универсальный газовый закон (Клапейрона): Давление смеси газов (закон Дальтона): Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону: Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
ТермодинамикаК оглавлению... Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле: Теплоемкость (С - большое) тела может быть рассчитана через удельную теплоёмкость (c - маленькое) вещества и массу тела по следующей формуле: Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом: Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное: При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное: При сгорании топлива выделяется количество теплоты равное: Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных): Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде: Работа идеального газа: Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа: Изменение внутренней энергии рассчитывается по формуле: Первый закон (первое начало) термодинамики (ЗСЭ): Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const): Изобарный процесс (p = const): Изотермический процесс (T = const): Адиабатный процесс (Q = 0): КПД тепловой машины может быть рассчитан по формуле: Где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл: Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен: Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула): Относительная влажность воздуха может быть рассчитана по следующим формулам: Потенциальная энергия поверхности жидкости площадью S: Сила поверхностного натяжения, действующая на участок границы жидкости длиной L: Высота столба жидкости в капилляре: При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной: При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
ЭлектростатикаК оглавлению... Электрический заряд может быть найден по формуле: Линейная плотность заряда: Поверхностная плотность заряда: Объёмная плотность заряда: Закон Кулона (сила электростатического взаимодействия двух электрических зарядов): Где: k - некоторый постоянный электростатический коэффициент, который определяется следующим образом: Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле): Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его): Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра: Напряженность электрического поля, которую создает заряженная плоскость: Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой: Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой: В однородном электрическом поле существует связь между напряженностью поля и напряжением: Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов: Работа электрического поля в общем случае может быть вычислена также и по одной из формул: В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле: Определение потенциала задаётся выражением: Потенциал, который создает точечный заряд или заряженная сфера: Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле): Для диэлектрической проницаемости вещества верно следующее: Определение электрической ёмкости задаётся формулой: Ёмкость плоского конденсатора: Заряд конденсатора: Напряжённость электрического поля внутри плоского конденсатора: Сила притяжения пластин плоского конденсатора: Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора): Объёмная плотность энергии электрического поля:
Электрический токК оглавлению... Сила тока может быть найдена с помощью формулы: Плотность тока: Сопротивление проводника: Зависимость сопротивления проводника от температуры задаётся следующей формулой: Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления): Закономерности последовательного соединения: Закономерности параллельного соединения: Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы: Закон Ома для полной цепи: Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника): Сила тока короткого замыкания: Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике: Мощность электрического тока: Энергобаланс замкнутой цепиПолезная мощность или мощность, выделяемая во внешней цепи: Максимально возможная полезная мощность источника достигается, если R = r и равна: Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле: Мощность потерь или мощность внутри источника тока: Полная мощность, развиваемая источником тока: КПД источника тока: ЭлектролизМасса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит: Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле: Где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
МагнетизмК оглавлению... Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле: educon.by
tetran.ru Значение фиВолновой анализ ► Урок 18: значение фи (φ)
Значение фи (φ)
Значение этого вездесущего явления было глубоко осмысленно и высоко оценено величайшими умами различных эпох. История изобилует примерами исключительно образованных людей, которые сохраняли особую притягательность к этой математической формуле. Пифагор отдавал предпочтение пятиконечной звезде, в которой каждый сегмент был в золотой пропорции по отношению к следующему меньшему сегменту, как символ его религиозного Ордена; у знаменитого математика 17 века Якоба Бернулли (Jacob Bernoulli)была Золотая спираль, выгравированная в камне; у Исаака Ньютона (Isaac Newton)была такая же спираль, вырезанная на спинке его кровати (принадлежащей сейчас Гравитационному фонду, Нью Бостон). Самыми ранними приверженцами были зодчие Египетских пирамид у города Гиза, которые закодировали знание о фи в своих конструкциях около 5000 лет назад. Египетские конструкторы сознательно внедрили Золотую пропорцию в Великую пирамиду, придав ее фасаду наклонную высоту в 1.618 раз больше половины ее основания так, что вертикальная высота пирамиды в то же самое время являлась корнем квадратным из длины половины основания, умноженной на 1.618. Согласно заявлению Питера Томпкинса (Peter Tompkins), автора Секретов Великой пирамиды (1971), «Это соотношение показывает, что сообщение Геродота (Herodotus; древнегреческий историк, 5 в. до н.э.*)действительно справедливо в том, что квадрат высоты пирамиды равен √φ* √φ = φ, и площадь фасада 1 * φ =φ». Более того, применяя эти соотношения, Египетские ученые (очевидно, для того, чтобы построить масштабную модель Северного полушария) использовали пи(π) и фи (φ) в подходе настолько математически изощренном, что он достигал искусства квадратуры круга и кубатуры сферы (т.е. создавая их равными по площади и объему), мастерство, которое не смогли повторить в течение более четырех тысячелетий. В то время как простое упоминание Великой пирамиды может служить высеченным из камня побуждением к скептицизму (возможно, по разумной причине), помните, что ее форма отражает ту же самую привлекательность, которую поддерживала западная научная, математическая, художественная и философская мысль, включая Платона, Пифагора, Бернулли, Кеплера, да Винчи и Ньютона. Те,кто сконструировал и построил эту пирамиду, несомненно, были блестящими естествоиспытателями, астрономами, математиками и инженерами. Ясно, что они хотели сохранить в течение тысячелетий Золотую пропорцию, как нечто, обладающее необыкновенной важностью. То, что людей такого масштаба позже увлекли величайшие умы Греции и эпохи Просвещения в их приверженности к этой пропорции, важно само по себе. Что касается причины, то все, что мы имеем, это гипотеза нескольких авторов. Однако эта гипотеза, какой бы непонятной ни была, странно подходит к нашим собственным наблюдениям. Было высказано предположение, что Великая пирамида в течение веков после того, как была построена, использовалась в качестве храма посвящения для тех, кто показал себя достойным понимания великих вселенских секретов. Только те, кто смог возвысится над примитивным восприятием вещей, какими они казались, для того, чтобы открыть то, чем в действительности они были, могли быть посвящены в «тайны», т.е. в систему истин вечного порядка и роста. Входило ли фи в такие «тайны»? Томпкинс объяснял:
«Египтяне времен фараонов, утверждает Швалер де Любиц(Schwaller de Lubicz), считали фи не числом, а символом созидательной функции или воспроизводства в бесконечной последовательности. Для них оно символизировало “огонь жизни, мужское семя, логос [на который ссылается] евангелие св. Иоанна”». Логос, греческое слово, было разносторонне определено Гераклитом (Heraclitus) и более поздними языческими,иудейскими и христианскими философами, обозначающим рациональный порядок вселенной, неотъемлемый закон природы, жизнеобразующую силу, сокрытую в вещах,созидательную силу вселенной, управляющей миром и насыщающей его. Читая это трудное для понимания и еще неясное описание, учтите, что те люди не могли ясно видеть все, что они чувствовали. У них не было графиков и Закона волн, чтобы сделать ясной модель развития природы, и они делали все, что могли, чтобы описать те организационные принципы, формирующие естественный мир, которые они разглядели. Если те древние философы были правы в том, что всемирная созидательная сила управляет и пронизывает вселенную, то почему бы ей не управлять и не насыщать мир человека? Если формы во всей вселенной, включая человеческое тело, мозг и ДНК отражают формы фи, может ли человеческая деятельность отражать ее так же? Если фи является жизненной силой во вселенной, может ли она быть побуждением в основе развития производственной деятельности человека? Если фи является созидательной функцией, может ли оно управлять созидательной деятельностью человека? Если развитие человека основано на производстве и воспроизводстве в «бесконечной последовательности», разве не разумно то, что такой процесс обладает спиральной формой фи и что эта форма различима в движении совокупной оценки его производственного потенциала, т.е. фондового рынка? Так же, как посвященные египтяне изучали скрытые истины построения и роста во вселенной за видимыми случайностями и хаосом (нечто, что, наконец, вновь открыла современная «теория хаоса» в 1980х), так и фондовый рынок, по нашему мнению, может быть должным образом истолкован, если рассматривать его суть, а не то, чем он кажется при поверхностном рассмотрении. Фондовый рынок – это не случайная бесформенная неразбериха, реагирующая на текущие события, но удивительно точная запись строгой структуры развития человечества. Сравните эту концепцию со словами астронома Вильяма Кингсланда (William Kingsland) в книге Великая пирамида в фактах и теории о том, что египетские астрономия/астрология была «наукой для особо посвященных,связанной с великими периодами человеческой эволюции». Закон волн объясняет великие периоды человеческой эволюции и показывает, как и почему они развиваются именно так. Более того, он охватывает и в микро-, и в макро-масштабе все, что базируется на парадоксальном принципе динамизма и изменения в пределах неизменной формы. Именно эта форма создает структуру и единство вселенной. Ничего в природе не предполагает, что жизнь является чем-то беспорядочным или бесформенным. Слово «вселенная» означает «единый порядок». Если жизнь обладает формой, тогда мы не должны отрицать возможность того, что человеческое развитие, которое является частью реальности жизни, также обладает порядком и формой. Если продолжить, то фондовый рынок,который оценивает производственную предприимчивость человека, также должен обладать порядком и формой. Все технические подходы к постижению рынка зависят от основного закона порядка и формы. Теория Эллиотта, тем не менее, продвигается дальше других. Она гласит, что не важно, насколько маленькой или насколько большой является форма, основная модель остается неизменной. Эллиотт в своей второй монографии использовал название Закон Природы – секрет Вселенной в предисловии к Закону волн и применил его ко всем видам человеческой деятельности. Возможно, Эллиотт зашел слишком далеко в высказывании, что Закон волн является секретом вселенной, так как природа создала множество форм и процессов, а не только одну простую композицию. Тем не менее, некоторые величайшие ученые прошлого, упомянутые ранее, возможно,согласились бы с формулировкой Эллиотта. Как минимум, следует сказать, что Закон волн является одним из самых важных секретов вселенной. Даже такое претенциозное утверждение поначалу может показаться практически настроенным инвесторам только хвастливой болтовней, вполне понятно почему. Великая природа этой концепции усиливает воображение и приводит в замешательство интеллект, в то время как ее применимость еще не ясна. Сначала мы должны сказать можем ли мы и теоретически предполагать, и воочию наблюдать, что действительно существует закон, который функционирует на той же математической основе на небесах и на земле так же, как и на фондовом рынке? Ответ – да. Фондовый рынок обладает именно такой же математической основой, как и природные явления. Идеализированная концепция Эллиотта о развитии рынка является превосходной основой, с которой необходимо строить Золотую спираль, как показывает рис.3-10 в грубом приближении. В этой конструкции вершина каждой последующей волны старшего волнового уровня является точкой соприкосновения с логарифмическим развитием.
Рисунок 3-10
Такой результат возможен, потому что на каждом уровне деятельности фондового рынка, бычий рынок подразделяется на пять волн, а медвежий рынок – на три волны, давая нам соотношение 5-3, т.е. математическую основу Закона волн Эллиотта. Мы можем воспроизвести полную последовательность Фибоначчи, как мы впервые сделали на рис.1-4, используя концепцию Эллиотта о развитии рынка. Если мы начнем с простейшего выражения концепции медвежьего движения, мы получим одну прямую нисходящую линию. Бычий взлет в простейшей форме является одной прямой восходящей линией. Полный цикл – две линии. На следующем уровне сложности, соответствующие числа 3, 5 и 8. Как показано на рис.3-11, эта последовательность может быть продолжена до бесконечности.
Рисунок 3-11
Следующий урок: Фи и фондовый рынок pro-forexinform.ru |
|
||||||||||||||||||
|
|
||||||||||||||||||
|












