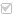Формула энергии конденсатора. Энергия запасенная в конденсатореЭнергия запасенная в конденсаторе « Учи физику!Конденсаторы изготовляют для разных целей. В некоторых электрических цепях применение конденсаторов позволяет пропускать быстрые изменения потенциалов, но задерживать их медленные изменения. (Иначе говоря, как будет видно ниже, переменный ток может проходить через конденсаторы, в то время как постоянный — нет.) В других устройствах конденсаторы используются для того, чтобы накапливать на короткое время заряд, или электрическую энергию. На рисунке показан высоковольтный конденсатор, предназначенный для накопления энергии. Он имеет емкость в 1 микрофараду и рассчитан на разность потенциалов в 2000 вольт. В качестве диэлектрика в нем используется масло, что обеспечивает более высокую диэлектрическую проницаемость, чем воздух, и позволяет предотвратить проскакивание искр между пластинами.
Работа, совершаемая при переносе очередной небольшой порции заряда от нижней пластины к верхней, равна произведению имеющейся разности потенциалов на переносимый заряд: A2=U1Δq2, Когда переносится последняя порция заряда от нижней пластины к верхней, совершаемая работа равна произведению этого заряда на полную разность потенциалов в конденсаторе. Среднее значение разности потенциалов, через которую переносились заряды, равна половине окончательной разности потенциалов. Поэтому работа, совершаемая при зарядке конденсатора, равна qU/2, где U — разность потенциалов между пластинами, часто называемая «электрическое напряжение». Эта работа равна энергии W запасенной в конденсаторе.
Автор Кл. Э. Суорц “Необыкновенная физика обыкновенных явлений” Интересные научные игрушки
Формула расчета энергии конденсаторов, как зарядить плоский конденсаторКонденсаторы являются неотъемлемой частью электрических схем. В большинстве случаев оперируют такими понятиями, как емкость и рабочее напряжение. Эти параметры являются основополагающими. Конденсаторы различных типов В некоторых случаях для более полного понимания работы упомянутого элемента необходимо иметь представление, что означает энергия заряженного конденсатора, как она вычисляется и от чего зависит. Определение понятия энергииНаиболее просто вести рассуждения применительно к плоскому конденсатору. В основе его конструкции лежат две металлических обкладки, разделенные тонким слоем диэлектрика. Плоский конденсатор Если подключить емкость к источнику напряжения, то нужно обратить внимание на следующее:
Данные соображения позволяют сделать вывод, что формулу энергии заряженного конденсатора можно получить несколькими способами. Вывод формулыЭнергия заряженного плоского конденсатора наиболее просто определяется, исходя из работы по сближению обкладок. Рассмотрим силу притяжения единичного заряда одной из обкладок к противоположной: F=q0E. В данном выражении q0 – величина заряда, E – напряженность поля обкладки. Поскольку напряженность электрического поля определяется из выражения: E=q/(2ε0S), где:
формулу силы притяжения можно записать как: F=q0 q/(2ε0S). Для всех зарядов сила взаимодействия между обкладками, соответственно, составляет: F=q2/(2ε0S). Работа по сближению пластин равняется произведению силы взаимодействия на пройденное расстояние. Таким образом, энергия заряженного конденсатора определяется выражением: W=A=Fd. Важно! В приведенном выражении должна быть разница в положениях пластин. Записывая только одну величину d, подразумеваем, что конечным результатом будет полное сближение, то есть d2=0. С учетом предыдущих выражений можно записать: W=d q2/(2ε0S). Известно, что емкость плоского конденсатора определяется из такого выражения: C=d/(ε0S). В результате энергия определяется как: W=q2/(2С). Полученное выражение неудобно тем, что вызывает определенные затруднения определения заряда на обкладках. К счастью, заряд, емкость и напряжение имеют строгую взаимосвязь: q = С U. Теперь выражение принимает полностью понятный вид: W=CU2/2. Полученное выражение справедливо для конденсаторов любых типов, не только плоских, и позволяет без затруднений в любой момент времени определять накопленную энергию. Емкость обозначается на корпусе и является величиной постоянной. В крайнем случае ее несложно измерять, используя специальные приборы. Напряжение измеряется вольтметром с необходимой точностью. К тому же очень просто зарядить конденсатор не полностью (меньшим напряжением), снизив, таким образом, запасенную энергию. Для чего необходимо знать энергиюВ большинстве случаев применения емкостей в электрических цепях понятие энергии не употребляется. Особенно это относится к время,- и частотозадающим цепям, фильтрам. Но есть области, где необходимо использовать накопители энергии. Наиболее яркий пример –фотографические вспышки. В накопительном конденсаторе энергия источника питания накапливается сравнительно медленно – несколько секунд, но разряд происходит практически мгновенно через электроды импульсной лампы. Конденсатор, подобно аккумулятору, служит для накопления электрического заряда, но между этими элементами есть много различий. Емкость аккумулятора несравненно выше, чем у конденсатора, но последний способен отдать ее практически мгновенно. Лишь недавно, с появлением ионисторов, это различие несколько сгладилось. Ионистор Какова же ориентировочная величина энергии? Можно для примера вычислить ее для уже упомянутой фотовспышки. Пускай, напряжение питания составляет 300 В, а емкость накопительного конденсатора – 1000 мкФ. При полном заряде величина энергии составит 45 Дж. Это довольно большая величина. Прикосновение к выводам заряженного элемента может привести к несчастному случаю. Конденсатор фотовспышки Важно! Принудительный разряд путем закорачивания выводов металлическими предметами чреват выходом устройства из строя. Накопленная энергия конденсатора способна за долю секунды расплавить выводы внутри элемента и вывести его из строя. ВидеоОцените статью:elquanta.ru Энергия поля конденсатора - Основы электроникиВся энергия заряженного конденсатора сосредотачивается в электрическом поле между его пластинами. Энергию, накопленную в конденсаторе, можно определить следующим образом. Представим себе, что мы заряжаем конденсатор не сразу, а постепенно, перенося электрические заряды с одной его пластины на другую. При перенесении первого заряда работа, произведенная нами, будет небольшой. На перенесение второго заряда мы затратим больше энергии, так как в результате перенесения первого заряда между пластинами конденсатора будет уже существовать разность потенциалов, которую нам придется преодолевать, третий, четвертый и вообще каждый последующий заряд будет переносить все труднее и труднее, т. е. на перенесение их придется затрачивать все больше и больше энергии. Пусть мы перенесем таким образом некоторое количество электричества, которое мы обозначим буквой Q. Вся энергия, затраченная нами при заряде конденсатора, сосредоточится в электрическом поле между его пластинами. Напряжение между пластинами конденсатора в конце заряда мы обозначим буквой U. Как мы уже заметили, разность потенциалов в процессе заряда не остается постоянной, а постепенно увеличивается от нуля — в начале заряда — до своего конечного значения U. Для упрощения вычисления энергии допустим, что мы перенесли весь электрический заряд Q с одной пластины конденсатора на другую не маленькими порциями, а сразу. Но при этом мы должны считать, что напряжение между пластинами конденсатора было не ноль, как в начале заряда, и не U, как в конце заряда, а равнялось среднему значению между нулем и U, т. е. половине U. Таким образом, энергия, запасенная в электрическом поле конденсатора, будет равна половине напряжения U, умноженной на общее количество перенесенного электричества Q. Полученный результат мы можем записать в виде следующей математической формулы: W = UQ/2 (1) Если напряжение в этой формуле будет выражено в вольтах, а количество электричества — в кулонах, то энергия W получится в джоулях. Если мы вспомним, что заряд, накопленный на конденсаторе, равен Q = CU, то формулу (1) можно будет записать окончательно в следующем виде: W = CU2/2 (2) Выражение (2) говорит нам о том, что энергия, сосредоточенная в поле конденсатора, равна половине произведения емкости конденсатора на квадрат напряжения между его пластинами. Этот вывод имеет очень важное значение при изучении раздела радиотехники о колебательных контурах. ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! Похожие материалы:Добавить комментарийwww.sxemotehnika.ru Энергия конденсатораГоспода, всем приветище! Сегодня речь пойдет про энергию конденсаторов. Внимание, сейчас будет спойлер: конденсатор может накапливать в себе энергию. Причем иногда очень большую. Что? Это не спойлер, это и так было всем очевидно? Здорово если так! Тогда поехали в этом более подробно разбираться! В прошлой статье мы пришли к выводу, что заряженный конденсатор, отсоединенный от источника напряжения, может сам в течении некоторого времени (пока не разрядится) давать некоторый ток. Например, через какой-то резистор. По закону Джоуля-Ленца если через резистор течет ток, то на нем выделяется тепло. Тепло – значит, энергия. И берется эта самая энергия из конденсатора – больше, собственно, неоткуда. Значит, в конденсаторе может хранится некоторая энергия. Итак, физика процессов более-менее понятна, поэтому теперь давайте поговорим, как это все описать математически. Потому что одно дело все описать на словах – это круто, замечательно, это должно быть, но в жизни часто надо что-то рассчитать и тут уже обычных слов не достаточно. Для начала давайте вспомним определение работы из механики. Работа A силы F это произведение этой самой силы F на вектор перемещения s.
Полагаю, что механику вы изучали когда-то и это знаете
Вспомним теперь статью про закон Кулона. Мы там получили замечательную формулу, которую сейчас самое время вспомнить:
То есть, если у нас есть электрическое поле с напряженностью Е и мы в него помещаем некоторый заряд q, то на этот заряд будет действовать сила F, которую можно рассчитать по этой формуле. Нам никто не мешает подставить эту формулу в чуть выше написанную формулу для работы. И таким образом найти работу, которую совершает поле при перемещении в нем заряда q на расстояние s. Будем полагать, что мы перемещаем наш заряд q точно по направлению силовых линий поля. Это позволяет использовать формулу работы без векторов:
Теперь, господа, внимание. Напоминаю одну важную штуку из той же механики. Есть такой особый класс сил, которые называются потенциальные. Если говорить упрощенным языком, то для них верно утверждение, что если эта сила на каком-то отрезке пути совершила работу А, то это значит, что в начале этого пути у тела, над которым совершалась работа, энергия была на это самое А больше, чем в конце. То есть на сколько поработали, на столько и изменилась потенциальная энергия. Работа потенциальных сил не зависит от траектрии и определяется только начальной и конечной точкой. А на замнкнутом пути она вообще равна нулю. Как раз-таки сила электрического поля относится к этому классу сил. Вот мы помещаем наш зарядик q в поле. Он под действием этого поля перемещается на некоторое расстояние от точки С до точки D. Пусть для определенности в точке D энергия заряда будет равна 0. При этом перемещении поле совершает работу А. Из этого следует, что в начале пути (в точке C) наш зарядик обладал некоторой энергией W=A. То есть, мы можем записать
Теперь самое время рисовать картинки. Взглянем на рисунок 1. Это немного упрощенная иллюстрация физики процессов плоского конденсатора. Более полное мы рассматривали это в прошлый раз.
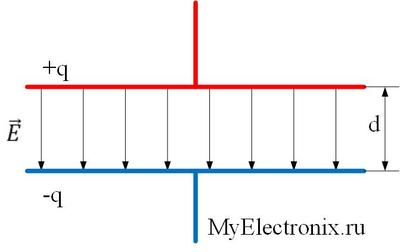
Рисунок 1 – Плоский конденсатор Давайте теперь чуть-чуть искривим свое сознание и глянем на наш конденсатор по-другому, чем раньше. Давайте предположим, что у нас за основу взята, например, синяя пластина. Она создает некоторое поле с некоторой напряженностью. Безусловно, и красная пластина тоже создает поле, но в данный момент это не интересно. Давайте смотреть на красную пластину, как на некоторый заряд +q, расположенный в поле синей пластины. И сейчас мы попробуем применить все вышеописанное к красной пластине как будто это и не пластина вовсе, а просто некоторый заряд +q. Вот так вот хитро. Почему, собственно, нет? Возможно, вы скажите – как же так, раньше мы везде исходили из того, что заряды у нас точечные, а тут – целая большая пластина. Она как-то на точку не совсем тянет. Спокойствие, господа. Никто нам не мешает разбить красную пластину на огромную кучу маленьких частичек, каждую из которых можно считать точечным зарядом Δq. Тогда уже можно без проблем применять все вышеописанное. И если мы выполним все расчеты сил, напряженностей, энергий и прочего для вот таких вот отдельных Δq и потом сложим результаты между собой, то получится, что мы зря так переусердствовали – результат будет ровно таким же, как если бы мы просто при расчетах брали заряд +q. Кто хочет – может проверить, я только за Итак, вернемся к рисунку 1. На нем показано, что между обкладками конденсатора существует поле с некоторой напряженностью Е. Но мы договорились сейчас разделить роли обкладок – синяя у нас источник поля, а красная – заряд в поле. Какое же поле создает одна синяя обкладка отдельно от красной? Какова его напряженность? Очевидно, что она в два раза меньше общей напряженности. Почема это так? Да потому, что если забыть про нашу абстракцию (типа красная пластина – и не пластина вовсе, а просто заряд), то в результирующую напряженность Е вносят одинаковый вклад обе обкладки – и красная, и синяя: каждая по Е/2. В результате суммы этих Е/2 как раз и получается та самая Е, которая у нас на картинке. Таким образом (отбрасывая вектора), можно записать
Теперь посчитаем, если можно так выразиться, потенциальную энергию красной обкладки в поле синей обкладки. Заряд мы знаем, напряженность мы знаем, расстояние между обкладками тоже знаем. Поэтому смело записываем
Идем дальше. На деле же никто не мешает поменять местами красную и синюю обкладки. Давайте рассуждать наоборот. Будем рассматривать теперь красную обкладку как источник поля, а синюю – как некоторый заряд –q в этом поле. Думаю, даже без проведения расчета будет очевидно, что результат будет точно такой же. То есть энергия красной пластины в поле синей пластины равна энергии синей пластины в поле красной пластины. И, как вы возможно уже догадались, это и есть энергия конденсатора. Да, вот по этой самой формуле можно произвести расчет энергии заряженного конденсатора:
Слышу, как мне уже кричат: стоп, стоп, опять ты втираешь мне какую-то дичь! Ну ладно, расстояние между пластинами я еще как-то смогу измерить. Но меня почему-то опять заставляют считать заряд, что не понятно как сделать, да еще и напряженность надо знать, а чем я ее померяю?! Мультиметр вроде как не умеет это делать! Все верно, господа, сейчас мы займемся преобразованиями, которые позволят вам измерить энергию конденсатора всего лишь с применением обыкновенного мультиметра. Давайте сперва избавимся от напряженности. Для этого вспомним замечательную формулу, которая связывает напряженность с напряжение:
Да, напряжение между двумя точками в поле равно произведению напряженности этого поля на расстояние между этими двумя точками. Итак, подставляя это полезнейшее выражение в формулу для энергии, получаем
Уже легче, напряженность ушла. Но остался еще заряд, который не понятно как мерить. Что бы от него избавиться, давайте вспомним формулу емкости конденсатора из предыдущей статьи:
Да, для тех, кто забыл, напоминаю, что емкость определяется как отношение этого злополучного заряда, накопленного конденсатором, к напряжению на конденсаторе. Давайте из этой формулы выразим заряд q и подставим его в формулу энергии конденсатора. Получаем
Вот это уже дельная формула, для энергии заряженного конденсатора! Если нам нужно узнать, какая энергия запасена в конденсаторе с емкостью С, заряженного до напряжения U, мы вполне можем это сделать по вот этой вот формуле. Емкость С обычно пишется на самом конденсаторе или на его упаковке, а напряжение всегда можно измерить мультиметром. Из формулы видно, что энергии в конденсаторе тем больше, чем больше емкость самого конденсатора и напряжение на нем. Причем энергия растет прямо пропорционально квадрату напряжения. Это важно помнить. Увеличение напряжения гораздо быстрее приведет к росту энергии, запасенной в конденсаторе, чем увеличение его емкости. Для особых любителей зарядов можно из формулы определения емкости выразить не заряд, а напряжение и подставить его в формулу для энергии конденсатора. Таким образом, получаем еще одну формулу энергии
Используется эта формула довольно редко, а на практике вообще не припомню, что б по ней что-то считал, но раз она есть, то путь тут тоже будет для полноты картины. Самая ходовая формула – это средняя. Давайте для интереса произведем некоторые расчеты. Пусть у нас есть вот такой вот конденсатор
Рисунок 2 – Конденсатор И давайте мы его зарядим до напряжения, скажем, 8000 В. Какая энергия будет запасена в таком конденсаторе? Как мы видим из фотографии, емкость данного конденсатора составляет 130 мкФ. Теперь легко выполнить расчет энергии:
Много это или мало? Безусловно, не мало! Даже очень не мало! Скажем так, разрешенная энергия электрошокеров составляет какие-то там смешные единицы джоулей, а тут их тысячи! Принимая во внимание высокое напряжение (8кВ) можно смело утверждать, что для человека контакт с таким заряженным конденсатором скорее всего закончится очень и очень печально. Следует соблюдать особую осторожность при больших напряжениях и энергиях! У нас был случай, когда произошло короткое замыкание нескольких таких вот конденсаторов, соединенных параллельно и заряженных до нескольких киловольт. Господа, это было зрелище не для слабонервных! Бабахнуло так, что у меня потом в ушах пол дня звенело! А на стенах лаборатории осела медь от расплавленных проводов! Спешу успокоить, никто не пострадал, но это стало хорошим поводом дополнительно подумать над способами отвода такой гигантской энергии в случае нештатных ситуаций. Кроме того, господа, важно всегда помнить, что конденсаторы блоков питания приборов тоже не могут мгновенно разрядиться после отключения прибора от сети, хотя там, безусловно, должно быть какие-то цепи, предназначенные для их разряда. Но должны быть, это не значит, что они там точно есть Итак, господа, сегодня мы познакомились с различными методами расчета энергии, запасенной в конденсаторе, а также обсудили, как эти расчеты можно выполнять на практике. На этом потихоньку закругляемся. Всем вам удачи, и до новых встреч! Вступайте в нашу группу Вконтакте Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it. myelectronix.ru 4КонденсаторыКонденсаторы. Принцип действия С основан на способности накапливать электрические заряды при приложении U между обкладками. Количественной мерой способности накапливать электрические заряды является ёмкость конденсатора. В простейшем случае конденсатор представляет собой две металлические пластины, разделенные слоем диэлектрика. Емкость такого конденсатора описывается формулой в 1 окне. Энергия, запасенная в конденсаторе описывается формулой Д. По назначению конденсаторы делятся на конденсаторы общего назначения (НЧ и ВЧ) и специального назначения (высоковольтные, помехоподавляющие, импульсные, дозиметрические, C с электрически управляемой емкостью (варикапы, вариконды). По назначению конденсаторы подразделяются на контурные, разделительные, блокировочные, фильтровые и т.д. По характеру изменения емкости на постоянные, переменные и полупеременные (подстроечные). По материалу диэлектрика различают три вида конденсаторов: с твердым, газообразным (воздух) и жидким диэлектриком (конденсаторное масло). Конденсаторы с твердым диэлектриком делятся на керамические, стеклянные, стеклокерамические, стеклоэмалевые, слюдяные, бумажные, электролитические, полистирольные, фторопластовые и др. По способу крепления различают конденсаторы для навесного и печатного монтажа, для микромодулей и микросхем. Конденсаторы гибридных ИМС представляют собой трехслойную структуру: на подложку наносится металлическая пленка, затем диэлектрическая пленка (Al2O3, Nb2O5, Ta2O5- оксиды данных металлов при малой толщине – диэлектрики) и снова металлическая пленка (окно 4). Основными параметрами являются ёмкость и рабочее напряжение (2 таблица в 1 окне). Кроме того, свойства конденсаторов характеризуются рядом паразитных параметров. Номинальная емкость Сном (основная ед.измерения –пФ – иногда не указывается) и допустимое отклонение от номинала ±∆С (3 таблица в 1 окне). Электрическая прочность конденсаторов Епр=Uпроб/h характеризуется величиной напряжения пробоя и зависит в основном от изоляционных свойств диэлектрика. Для повышения надежности РЭА конденсаторы используют при U, которое меньше номинального. Стабильность емкости определяется ее изменением под воздействием внешних факторов. Наибольшее влияние на величину емкости оказывает температура. Ее влияние оценивается температурным коэффициентом емкости (ТКЕ: М-отрицательный, П- положительный, МП0-приблизительно равный 0 )(окно 1 формула Ж, таблица 1, рис.А). В основном же изменение емкости вызывается изменением диэлектрической проницаемости. У высокочастотных конденсаторов величина ТКЕ не зависит от температуры и указывается на корпусе конденсатора путем окраски корпуса в определенный цвет и нанесения цветной метки. У НЧ керамических конденсаторов температурная зависимость емкости носит нелинейный характер. Температурная стабильность (ТСЕ, формула И в 1 окне) этих конденсаторов оценивается величиной предельного отклонения емкости при крайних значениях температуры. Обозначается Н10…Н90 (окно1 Б), число показывает на сколько процентов изменится емкость в рабочем интервале температур по сравнению с емкостью, измеренной при 200С. Потери энергии в конденсаторах обусловлены электропроводностью и поляризацией диэлектрика и характеризуются тангенсом угла диэлектрических потерь tgδ. Конденсаторы с керамическим диэлектриком имеют tgδ >>10-4, конденсаторы со слюдяным диэлектриком - 10-4, с бумажным - 0,01-0,02, с оксидным-0,1-1,0. С ростом частоты и температуры потери возрастают. Величина, обратная tgδ называется добротностью Q. Система обозначений конденсаторов постоянной емкости состоит из ряда элементов: на первом месте стоит буква К, на втором месте - двухзначное число,1 обозначает тип диэлектрика, а2 - особенности диэлектрика или эксплуатации , затем через дефис ставится порядковый номер разработки. Например, обозначение К 10-12(окно 1 А) означает - керамический низковольтный конденсатор (U<1600B) с 12 порядковым номером разработки. K-50 – электролитический фольговый алюминиевый (окно 1 Г), относятся к полярным, один из выводов как на корпусе, так и в УГО отмечается «+» (включать следует правильно, иначе выйдет из строя). Они могут работать при подведении к аноду + потенциала, а к катоду - отрицательного. Поэтому их применяют в цепях пульсирующего напряжения, полярность которого не изменяется, например, в фильтрах питания. Электролитические конденсаторы обладают очень большой емкостью (до тысячи мкФ) при сравнительно небольших габаритах. Но они не могут работать в ВЧ цепях, так как из-за большого сопротивления электролита tgδ достигает значения 1,0. Поскольку при низких t электролит замерзает, то в качестве параметра электролитических конденсаторов указывается минимальная t, при которой допустима работа C. При ↓температуры емкость конденсатора↓, а при ↑ температуры -↑. Вариконд (окно 7). Для него характерны высокие значения относительной диэлектрической проницаемости и ее сильная зависимость от напряженности электрического поля и температуры. Управляются напряжением. Выполняют на основе сегнетоэлектриков (титанатов бария, стронция, кальция – свойственна спонтанная поляризация). Применяются вариконды как элементы настройки колебательных контуров. Если вариконд включить в цепь резонансного LC-контура и изменять постоянное напряжение, подводимое к нему от источника, то можно изменять резонансную частоту этого контура (формула Е в окне 1). Максимум диэл. прониц-ти соответствует т. Кюри(Нееля) (сегнетоэлектрические св-ва при данной t пропадают). Варикап - это полупроводниковый конденсатор (диод, на основе p-n-перехода), емкость которого изменяется за счет внешнего напряжения. С ростом обратного напряжения емкость варикапа уменьшается (окно 3). Благодаря малым размерам, высокой добротности, стабильности и значительному изменению емкости варикапы нашли широкое применение в РЭА для настройки контуров и фильтров. В цепи переменного тока (окно 2) в емкостной цепи ток опережает по фазе на 900 напряжение. Эквивалентная емкость батареи параллельно включенных конденсаторов рассчитывается по формуле 2, емкостное сопротивление Xc такой цепи оценивается формулой 4 (определено формулой а, измеряется в Ом). Рабочим напряжением является наименьшее из напряжений конденсаторов, входящих в схему. В окне 2 изображено последовательное соед. 2 конденсаторов с разл. ёмкостью. Полное напряжение поделится между конденсаторами т.о., что на меньшей емкости установится большее U и наоборот: Конденсаторы применяют в разл. аппаратуре. Защитную (демпферную) функцию С вып. на 1 рис. в окне 6 (препятствует прохождению постоянной составляющей), функцию фильтра (на рис.2) и в качестве энергонакопителя (рис.3). Ионистор-кондесатор с двойным электрическим слоем, формируемым на границе 2 фаз, который обладает высокой емкостью (10-100 мкФ). Диэлектрика нет, вместо него водные растворы кислот, щелочей, твердые электролиты.Uрабмало. studfiles.net
masters.donntu.org Формула энергии конденсатора, WpКак любой проводник, несущий заряд, конденсатор имеет энергию, которую находят по формуле: где q – заряд конденсатора; C – емкость конденсатора; Связь энергии конденсатора и силы взаимодействия его пластинМеханическую (пондемоторную) силу, с которой пластины плоского конденсатора взаимодействуют между собой можно найти, если использовать формулу (1). Допустим, что расстояние между пластинами конденсатора изменяют от x до При этом потенциальная энергия взаимодействия пластин уменьшается на: Тогда силу, которая выполняет работу можно представить как: Емкость плоского конденсатора равна: Значит, формулу энергии плоского конденсатора запишем как: Подставим в (4) выражение для энергии (6), получим: В выражении (7) минус показывает, что пластины конденсатора притягиваются друг к другу. Энергия электростатического поля плоского конденсатораЕсли вспомнить, что разность потенциалов между обкладками плоского конденсатора равна: где расстояние меду пластинами конденсатора мы обозначили d, и приняв во внимание, что для плоского конденсатора емкость определена выражением (5) тогда имеем: где Примеры решения задач по теме «Энергия конденсатора»ru.solverbook.com |
|
||||||||||||||||||
|
|
||||||||||||||||||
|
. Страшные значки векторов нужны только в случае, если направление силы не совпадает с перемещением: вроде случая, когда сила тянет строго прямо, а перемещение идет под каким-то углом к силе. Такое бывает, например, когда груз перемещается по наклонной плоскости. Если же направление силы и перемещения совпадают, то можно смело отбросить вектора и просто перемножать силу на длину пути, получая таким образом работу:
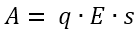
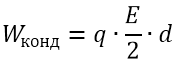
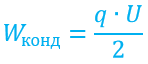
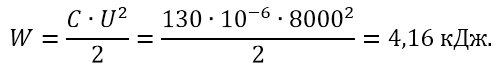
. Поэтому в любом случае после отключения любого прибора от сети, прежде чем лезть к нему внутрь, лучше подождать пару минут для разряда всех кондеров. И потом, после снятия крышки, прежде чем лапками хвататься за все подряд, следует сначала померить напряжение на силовых накопительных конденсаторах и при необходимости выполнить их принудительный разряд каким-нибудь резистором. Можно, конечно, просто отверткой замкнуть их выводы, если емкости не слишком большие, но такое делать крайне не рекомендуется!![\[ W_p=\frac{q\Delta \varphi }{2}=\frac{C{\left(\Delta \varphi \right)}^2}{2}=\frac{q^2}{2C}\ \qquad(1)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0d0a471cdcbe9e2138c913cdd83d6ba5_l3.png "Rendered by QuickLaTeX.com")
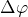– разность потенциалов между обкладками конденсатора. 
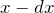. В таком случае, сила изменяющая расстояние между пластинами выполняет работу, равную:![\[dA=Fdx\ \qquad(2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-21afedd09d3b85cd4b5a7432a4201f09_l3.png "Rendered by QuickLaTeX.com")
![\[-dW_p=Fdx\ \qquad(3)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-dce3670d82de5f5cc81a5ba66c0dfc2f_l3.png "Rendered by QuickLaTeX.com")
![\[F=-\frac{dW_p}{dx} \qquad(4)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6080587c445c3cfde34923fbbece5609_l3.png "Rendered by QuickLaTeX.com")
![\[C=\frac{\varepsilon {\varepsilon }_0S}{x} \qquad(5)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3aed248de6812a0e6b710e7f51331b69_l3.png "Rendered by QuickLaTeX.com")
![\[W_p=\frac{q^2}{2\varepsilon \varepsilon_0S}x \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fe5460ff69582748fd806e2280210348_l3.png "Rendered by QuickLaTeX.com")
![\[F=-\frac{q^2}{2\varepsilon {\varepsilon }_0S} \qquad(7)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e70528d25d892bfda13c14c3fd36384a_l3.png "Rendered by QuickLaTeX.com")
![\[\Delta \varphi =Ed\ \qquad(8)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-711c072f98f0af4efe1c90bf92358cb3_l3.png "Rendered by QuickLaTeX.com")
![\[W_p=\frac{\varepsilon {\varepsilon }_0E^2}{2}Sd=\frac{\varepsilon {\varepsilon }_0E^2}{2}V\ \qquad(9)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ed16f1b0c45b7f173d282a1938b0ac99_l3.png "Rendered by QuickLaTeX.com")
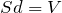– объем конденсатора; E – напряженность поля конденсатора. Формула (9) связывает энергию конденсатора с зарядом на его обкладках и напряженностью поля. 
