Значение словосочетания «падение напряжения». Что называется падением напряженияЗначение словосочетания ПАДЕНИЕ НАПРЯЖЕНИЯ. Что такое ПАДЕНИЕ НАПРЯЖЕНИЯ?
Источник: Википедия Делаем Карту слов лучше вместеПривет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю как устроен ваш мир. Помоги мне разобраться! Спасибо! Я стал чуточку лучше понимать мир эмоций. Вопрос: перетекание — это что-то положительное, отрицательное или нейтральное? Положительное Отрицательное Предложения со словом «падение напряжения»:
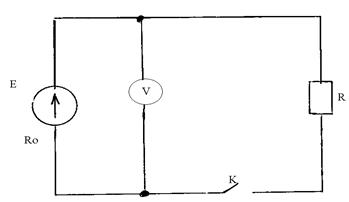
Оставить комментарийТекст комментария: kartaslov.ru Что такое падение напряжения? - Ремонт интерьер строительствоПадение напряженияПадение напряжения — это термин, используемый для описания любого снижения напряжения питания в полной электрической цепи. Этот термин может использоваться для описания потерь напряжения на конкретном компоненте в цепи, потерь напряжения, измеренных по всей цепи, или в качестве широкого описания явления потери напряжения в цепи в целом. Все электрические схемы, независимо от того, насколько просты, представляют определенную степень сопротивления потоку электрического тока через них. Это сопротивление эффективно усиливает работу электрического тока и, таким образом, поглощает энергию. Это расходование энергии приводит к уменьшению напряжения, описываемого термином падения напряжения. Например, простая схема может состоять из 9-вольтовой батареи, прикрепленной к простой лампе накаливания с помощью маленького переключателя. Если бы измерить напряжение на клеммах батарей с открытым переключателем, показание мультиметра будет приблизительно 9 вольт. Если нужно закрыть выключатель и осветить лампочку, это показание снизится примерно на 1,5 вольта. Это снижение напряжения — это то, что известно как падение напряжения, и это происходит в результате работы, которую батарея должна делать, чтобы осветить лампу. Каждый компонент в цепи, включая проводку, обеспечивает определенную степень сопротивления потоку электрического тока и вызывает связанное падение напряжения. В приложениях, которые являются чрезвычайно чувствительными к напряжению питания, например электронным устройствам, эти потери напряжения должны быть тщательно рассчитаны и напряжение питания отрегулировано таким образом, чтобы обеспечить их. Например, источник питания с постоянным током 12 В (DC), как правило, производит выход 13,8 вольт для удовлетворения этого явления падения напряжения. В приложениях, требующих очень длинных кабельных трасс, общепринятой практикой является использование довольно тяжелых кабелей, которые оказывают меньшее сопротивление потоку электрического тока в попытке минимизировать влияние потерь напряжения. Таким образом, полная потенциальная потеря напряжения в любой цепи должна быть тщательно рассчитана на этапе проектирования и спецификации проекта, чтобы гарантировать, что конечный результат соответствует всем требованиям. К счастью, любые потери напряжения в цепи можно вычислить с большой точностью, используя формулу падения напряжения. Это позволяет достичь согласованных и прогнозируемых результатов в конце установки. Эти расчеты будут различаться в зависимости от типа схемы, напряжения питания и задействованных компонентов и могут быть чрезвычайно сложными, часто требуя использования калькулятора падения напряжения. Тем не менее, они выполняют предположения о точном регулировании характеристик источника питания для обеспечения сопротивления цепи. voltstab.ru Часть ЭДС, затрачиваемая на перенос зарядов по внешнему участку цепи, называется падением напряжения во внешней цепи или просто напряжением и обозначается U.Термин «падение напряжения» или «напряжение» обозначает часть ЭДС, затрачиваемую на преодоление сопротивления данного участка цепи. ЭДС источника представляет собой сумму падений напряжения на внутреннем и внешнем участке цепи. Е = U + U0 Из этого равенства следует: U = E – U0 , т.е. напряжение на зажимах источника тока меньше его ЭДС на величину падения напряжения на внутреннем участке цепи. Напряжение измеряется в Вольтах. ЭДС и напряжения измеряется вольтметром (рис.1). 
Рис.1 ЭДС измеряют вольтметром на зажимах источника при отключенном потребителе (ключ К разомкнут). Напряжение измеряют там же, при включённом потребителе (ключ К разомкнут). Для измерения напряжения на каком-либо участке электрической цепи вольтметр нужно включить к концам этого участка (Рис.2). Внутреннее падение напряжения измерить нельзя! Его рассчитывают по формуле: U0 = E – U. Закон Ома для полной цепи с источником ЭДС
Сила тока, протекающего в замкнутой цепи прямо пропорциональна ЭДС источника и обратно пропорциональна сумме сопротивлений внешнего R и внутреннего Rо участков цепи.
I – сила тока; Е - ЭДС источника; R – сопротивление внешнего участка цепи; R0 – внутреннее сопротивление источника.
Закон Ома для участка цепи
Сила тока прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка. Основная формула:
Следствия:
ТЕМЫ ДЛЯ ЛАБОРАТОРНОЙ РАБОТЫ №1 ВТОРОЙ УРОВЕНЬ Работа и мощность электрического тока Работой электрического тока называется преобразование электрической энергии в другой вид энергии. A = Е· q Работа в системе СИ измеряется в джоулях [1 Дж = 1 В·А ·с] Где: А [ Дж ] – работа электрического тока в замкнутой цепи Е [ В ] - ЭДС источника q [ Кл ] – заряд. Имея в виду, что q = I · t, получаем A = Е· I · t Любая электрическая цепь состоит из двух участков – внутреннего и внешнего, следовательно: Е = U + U0.Введем данное выражение a формулу работы:
A = (U + U0)· I · t = U · I · t + U0· I · t. Из последней формулы видно, что ток совершает работу и на внутреннем, и на внешнем участках цепи. Разобьем данную формулу на две: A = U · I · t –работа, совершаемая током на внешнем участке цепи; А = U0· I · t -работа, совершаемая током на внутреннем участке цепи (нагрев источника). Величина, характеризующая скорость с которой происходит преобразование электрической энергии в другие виды энергии, или скорость с которой совершается работа, называется электрической мощность.
Где: P [Вт] – электрическая мощность А [Дж] - работа электрического тока t [с ] – время, в течение которого совершается работа
1 МВт = 1 ·106 Вт (мегаватт) 1 кВт = 1 ·103 Вт (киловатт) 1 мВт = 1·10-3 Вт (милливатт) 1 л.с. = 736 Вт. Величина, характеризующая скорость, с которой другие виды энергии преобразуются в источнике питания в электрическую, называется мощностью генератора.
Величина, характеризующая скорость, с которой происходит преобразование электрической энергии в потребителе в другие виды энергии, называется мощностью потребителя
Из этой формулы вытекают следующие: А используя закон Ома можно вывести еще и такие формулы:
Мощность, характеризующая непроизводительный расход электрической энергии, например внутри генератора, называется мощностью потерь.
По закону сохранения энергии мощность генератора равна сумме мощности потребителя и мощности потерь. PИ = P + P0
Соединение потребителей Последовательное соединение Соединение, при котором участки цепи включены один за другим без разветвлений и поэтому имеют одно значение тока, называется последовательным. (рис.4)
Рис.4 IAB = I1 = I2 = I3=…=In=const При последовательномсоединении резисторов, их эквивалентное (общее) сопротивление равно сумме сопротивлений всех резисторов, входящих в цепочку RАВ = R1+R2+R3+…+Rn
Если R1 = R2 = R3 , то RAB = n · R1 , где n – число сопротивлений. UAB = U1 + U2 + U3 Параллельное соединение
Соединение, при котором несколько ветвей присоединены к одной паре узлов, называется параллельным (рис.5). infopedia.su Полное падение - напряжение - Большая Энциклопедия Нефти и Газа, статья, страница 1Полное падение - напряжениеCтраница 1 Полное падение напряжения в столбе разряда благодаря малой напряженности поля не превышает обычно десятков вольт даже тогда, когда междуэлектродное расстояние I достаточно велико. [1] Полное падение напряжения в разряде называют также напряжением горения разряда. В газотроне оно обычно мало отличается от катодного падения напряжения ДЕ7К, поскольку небольшое положительное падение напряжения в столбе разряда компенсируется в большинстве случаев отрицательным анодным падением напряжения. [2] Полное падение напряжения в одной фазе линии представляется вектором АС, численно равным Iz I / r2 x2, где г - активное, ах - индуктивное сопротивления линии. Полное падение напряжения может быть разложено на продольную АД и поперечную СД составляющие. [3] Полное падение напряжения в контуре ( рис. IV.2.7) равно падению напряжения на активном сопротивлении UR. Это явление называется резонансом напряжений. [4] Полное падение напряжения в нагруженной линии, как видно из формулы ( 10 - 9), складывается из падения напряжения при холостом ходе линии At / фо, вызванного током 1Вг, и падения напряжения А. [6] Полное падение напряжения на диоде складывается из падения напряжения на электронно-дырочном переходе и на базе диода. [7] Полное падение напряжения на диоде складывается из падения напряжения на р - - переходе и на базе диода. [8] Полное падение напряжения на шунтах ( 75 В) соответствует полному отклонению стрелки прибора, 20 или 200 А. [9] Полное падение напряжения на диоде складывается из падения напряжения на p - n - переходе и на базе диода. [10] Полное падение напряжения на открытом биполярном ключе имеет также и омическую составляющую, определяемую сопротивлением низколегированных слоев структуры. С ростом температуры подвижность носителей уменьшается, и сопротивление омических слоев растет. [11] Зависимость полного падения напряжения в тиратроне от анодного тока при нормальном режиме иллюстрирует вольт-амперная характеристика тиратрона. [13] Таким образом, вектор полного падения напряжения от тока / л в сопротивлениях линии R и X будет равен ае, а его продольная и поперечная составляющие соответственно А. [15] Страницы: 1 2 3 4 5 www.ngpedia.ru Урок 8. Делим ток и роняем напряжениеСегодня мы поговорим о нескольких видах простейших электрических цепей и узнаем, как же можно уронить напряжение и разделить ток на несколько частей. Урок будет длиииииинный, но содержательный, с разбором задачи в конце. Начнем с давно забытого всеми урока за номером четыре, где велся разговор о законе Ома для полной цепи. Было указано, что сила тока в цепи зависит от суммы сопротивлений: внешнего (нагрузки) и внутреннего сопротивления источника. Однако, а почему это мы так вдруг решили, что от суммы, а не, например, от разности или корня квадратного? Бездоказательно, однако! Рассмотрим схему этой цепи, немного отступив от правил прошлого урока… «Ну вот, учили-учили, а теперь забываем применять?! – скажете вы.» Нет, эти правила действительно нужны и мы их будем применять, но только когда нам нужно нарисовать именно принципиальную схему устройства, а сейчас мы будем рассматривать некую небольшую абстрактную схему и для наглядности и простоты некоторых (только некоторых!) правил не будем придерживаться. Но для начала посмотрим, как изображается и обозначается на принципиальной электрической схеме давно уже известное нам сопротивление. Рисунок 8.1 – Источник питания с внутренним сопротивлением На этой схеме внутреннее сопротивление источника GB1 обозначено как r, а сопротивление внешней цепи (нагрузка) – как R. Причем, считаем, что R>>r. Здесь мы и отступаем от норм ГОСТ, поскольку для простоты понимания опускаем цифровые обозначения сопротивлений и добавляем на схему некоторые точки A, B и C. Такое включение сопротивлений называют последовательным, так как включены они как бы друг за другом – конец сопротивления r подключен к началу сопротивления R (точка B) и между ними нет больше каких-либо элементов или отводов. Закон Ома для полной цепи говорит, что ток, в электрической цепи зависит от сопротивления этой цепи и одинаков для всех элементов, то есть ток, протекающий через r, равен току, протекающему через R. Давайте рассмотрим этот момент с помощью метода доказательства «от противного». Предположим, что токи, протекающие через сопротивления различны. Ток через большее сопротивление R, исходя из закона Ома, должен быть меньше тока через r. В таком случае в точке B начал бы накапливаться заряд, поскольку ток, выходящий из точки B меньше тока, входящего в нее, а ток есть ни что иное, как отношение перенесенного полем заряда на время. Накапливаемый в точке B заряд создает в этой точке потенциал, который в некоторый момент времени сравняется с потенциалом положительной клеммы аккумулятора (точка A). В этом случае ток в цепи прекращается, поскольку при разности потенциалов двух точек равной нулю потенциальные энергии зарядов в этих точках равны, и работа поля равна нулю. Это умозаключение, кстати говоря, приводит нас к одному интересному выводу: между точками одинакового потенциала протекание электрического тока невозможно. Однако, электроны, образующие не скомпенсированный заряд в точке B постепенно будут поглощаться ионами материала, что приведет к снижению потенциала и возобновлению тока, который восстановит потенциал и опять прервёт сам себя. Но это бы противоречило закону Ома, который говорит, что ток в цепи всегда постоянен, а здесь имеет место прерывистый ток, значение которого зависит от времени. Соответственно, такой ситуации быть не может, мы пришли к противоречию. Если же мы представим, что r>>R, тогда ток через большее сопротивление r исходя из закона Ома должен быть меньше тока через R. В этом случае ток, втекающий в точку B будет меньше, чем ток, вытекающий из нее, что приведет к уменьшению числа свободных электронов в материале до нуля и ток опять прекратится. Со временем за счет дрейфа и превращения атомов материала в ионы свободные электроны вновь образуются, и ток возобновиться, но истощение заряда продолжится, и ток опять прекратит сам себя. То есть мы видим такую же ситуацию, как в первом случае. Остаётся только одно разумное решение: ток в последовательной цепи одинаков для каждого элемента этой цепи. В этом случае поддерживается постоянный баланс потенциалов всех точек цепи. Это не говорит о том, что потенциалы одинаковы! Это значит, что потенциал каждой точки строго определён протекающим в ней током.Теперь давайте разберемся, почему ток в цепи будет зависеть от суммы сопротивлений. Тут всё довольно просто. Последовательное соединение двух проводников приводит к увеличению длины эквивалентного проводника, а это в свою очередь – к росту сопротивления (формула из Урока 3). Отсюда запоминаем еще одно важное правило: эквивалентное сопротивление участка цепи с последовательно включенными сопротивлениями равно сумме этих сопротивлений.
А раз две точки имеют разный потенциал, то между ними есть напряжение, которое называют падением напряжения. Нетрудно догадаться, что падение напряжения на элементе пропорционально току, протекающему через него, так как величина тока регулирует количество заряда на концах элемента, т.е. разность потенциалов. По сути величина падения напряжения подчиняется закону Ома для участка цепи: UR=IR∙R, где IR – ток, протекающий через сопротивление,R – величина этого сопротивления.Для нашей схемы на Рисунке 8.1 справедливы следующие соотношения: UAB=I∙r,UBC=I∙R,UAC=I∙(R+r)=εGB1 Из этих соотношений хорошо видно, что падение напряжения – часть эдс источника, доставшаяся участку цепи. Часто на схемах можно встретить такие обозначения падения напряжения: Рисунок 8.2 – Обозначение падения напряжения Стрелку направляют в сторону уменьшения потенциала. Разумеется, на принципиальных электрических схемах падение напряжения указывать не допускается.Раз мы заговорили о последовательных цепях, наверное, существуют и параллельные? Да, действительно, такие соединения есть и выглядят они следующим образом: Рисунок 8.3 – Параллельное соединение сопротивлений Параллельным соединением называется такое соединение, при котором выходы элементов соединены в одних точках. На нашей схеме это точки A и B. Поскольку элементы имеют общие точки, разность потенциалов на этих элементах будет одинакова, как и падение напряжения. То есть, напряжение на параллельных ветвях электрической цепи одинаково. Для удобства дальнейшего рассмотрения процессов в электрических цепях введем такие понятия как: узел, ветвь и контур. Ветвью называют любой двухполюсник, входящий в цепь, например, на Рисунке 8.3 отрезок AB есть ветвь. Узлом называют точку соединения трех и более ветвей (на Рисунке 8.3 обозначены жирными точками. На рисунке 8.1 точки A, B и C не являются узлами). Контур – замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам. Например, контуром можно назвать параллельное соединение сопротивлений R1 и R2 на Рисунке 8.3Рассмотрим теперь, что происходит с токами ветвей I, I1 и I2: (I1+I2 )∙ε=I∙ε Таким образом, сокращая на ε: I=I1+I2 То есть, в параллельных ветвях происходит деление тока. Если перенести слагаемые I1 и I2 в левую часть уравнения, получим, что алгебраическая сумма токов в каждом узле электрической цепи равна нулю. Кроме I правила Кирхгофа существует еще и II правило Кирхгофа: алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме эдс ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю.
Возвращаясь к схеме на рисунке 8.3 возникает логичный вопрос: как же нам рассчитать эквивалентное сопротивление параллельных ветвей? Ясно, что формула для последовательной цепи сюда не подойдет. Давайте заменим сопротивления R1 и R2 одним эквивалентным сопротивлением: Рисунок 8.4 – Замена параллельных сопротивлений эквивалентным сопротивлением Теперь ничто не мешает нам применить закон Ома, чтобы рассчитать Rэкв: Схема на рисунке 8.3 называется делитель тока и находит широкое применение. Более подробно применение делителя тока мы рассмотрим позже, а сейчас приведем такой пример, чтобы хоть немного убедить читателя в полезности этого схемного решения. Рассмотрим схему на рисунке 8.4. Допустим, эдс источника ε=5В, а сопротивление нагрузки Rэкв=1Ом, тогда мощность, выделяемая в нагрузке равна: Давайте немного изменим эту схему, пренебрегая внутренним сопротивлением и добавив еще одно сопротивление во внешнюю цепь: Рисунок 8.5 – Последовательное соединение сопротивлений По сути, это та же схема последовательного соединения двух сопротивлений, только теперь оба эти сопротивления являются частью нагрузки. Из вышеприведенных соотношений видно, что напряжение на каждом сопротивлении определяется протекающим током и значением этого сопротивления. Используя закон Ома, выразим величину тока, протекающего через сопротивления: Рисунок 8.6 – Смешанное соединение сопротивлений Как мы видим, сопротивления R2 и Rн включены параллельно, а их эквивалентное сопротивление включено последовательно с R1. Теперь сформулируем условия задачи: на нагрузке мощностьюPн=20 Вт необходимо получить напряжение Uн=5 В, если имеется аккумуляторная батарея номинальной эдс ε=12 В.Для начала обозначим направления протекания токов в каждой ветви. Рисунок 8.7 – Направления протекания токов Рассчитаем параметры нагрузки по известной мощности и напряжению: I2=0.1Iн=0.4 А Напряжение Uн равно напряжению UR2, так как эти сопротивления включены параллельно, значит, сопротивление R2 из закона Ома равно:
Для начала давайте рассчитаем его, используя второй способ, а потом сравним результаты.Поскольку нижним плечом делителя является эквивалентное сопротивление параллельно включенных сопротивлений R1 и Rн, рассчитаем его: I1=I2+Iн=0.4А + 4А = 4.4А Результаты совпали, значит, расчет выполнен верно.Рассчитаем величину сопротивления R1, пользуясь опять же законом Ома: PGB1=ε∙I1=12В ∙ 4.4А = 52.8Вт Тогда кпд равен: PR1=I12∙R1=(4.4 А)2∙1.136 Ом=30.8 ВтPR2=I22∙R2=(0.4 А)2∙1.59 Ом=2 Вт Сразу видно, что наибольшие потери рассеиваются на сопротивлении R_1. Величину тока мы значительно изменить не можем, так как она не может быть меньше величины тока нагрузки. Можно подкорректировать величину заданного нами тока I2… Стоп. А зачем нам вообще это сопротивление? Ведь делитель может быть собран с помощью самой нагрузки в качестве нижнего плеча! Смело убираем R2 из схемы. Рисунок 8.8 – Модернизированная схема Теперь нам не нужен этот «паразитный» ток I2. Пересчитаем величину сопротивления R1: PR1=Iн2∙R1=(4 А)2∙1.75 Ом=28 Вт И кпд: Теперь посмотрим, что будет, если мы изменим параметры нагрузки, например, вместо 20 Вт подключим 15 Вт. Изменится величина сопротивления нагрузки, ведь она определена номинальными значениями мощности и напряжения: Uн=ε-UR1=12 В-6.15 В=5.85 В Получается, что мы превысили номинальное напряжение на ≈17%. И нельзя точно сказать, выдержит ли наша нагрузка такого превышения. А может она попросту выйдет из строя… Получается, что без изменения R1 подключать нагрузку, отличную от расчетной, нельзя. Это и есть второй недостаток схемы делителя. В основном эта схема применяется там, где мощность потерь невелика, например, в цепях с силой тока единицы – десятки миллиампер. Теперь кратко опишем важные моменты урока, а на этом я с вами прощаюсь, ждем следующего урока, в котором подробно разберем задачу на расчет сложной электрической цепи.
← Урок 7. Основы составления электрических схем | Содержание | → myblaze.ru |
|
||||||||||||||||||
|
|
||||||||||||||||||
|
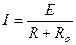, где
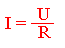
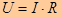-физический смысл данной формулы: сила тока тем больше, чем выше напряжение. В свою очередь напряжение больше там, где больше напряжение.
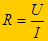- данная формула физического смысла не имеет, т.е. сопротивление не зависит ни от силы тока ни от напряжения. Эта формула используется только для расчета сопротивления.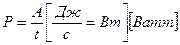
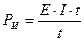→ PИ = E· I
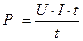→ Р= U· I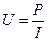
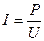
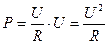
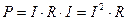
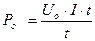→ Ро= Uо· I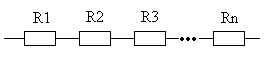
Как видите, это обычный прямоугольник, размерами 10мм*4мм.Итак, наша схема будет состоять из двух сопротивлений и идеального источника, нарисуем ее.
Наш вывод относительно протекания тока между точками одинакового потенциала приводит к тому, что точки A, B и C обладают различными потенциалами, раз ток в цепи существует. Причем потенциал точки C меньше потенциала точки B, а точки B меньше, чем точки A. Почему? А потому что уменьшение количества свободных электронов (за счет столкновения с узлами кристаллической решётки и прочих потерь в материале) происходит последовательно от «минуса» аккумулятора (он же является их источником!) через сопротивления R и r к «плюсу» аккумулятора (а он уже является источником положительных ионов). К тому же мы ведь считаем, что ток «течет» от «плюса» к «минусу», а электроны наоборот – от «минуса» к «плюсу», поэтому, исходя из формулы Урока 3 для потенциальной энергии заряда, видно, что наибольшим потенциалом обладает точка с наименьшим зарядом, – «плюс» аккумулятора.
Эти соотношения получаются из довольно простого логического заключения: если источник включен параллельно сопротивлению, то падение напряжения на сопротивлении не может быть отличным от эдс источника, ведь потенциалы концов сопротивления R1 соответственно равны потенциалам концов сопротивления R2. Причем не играет роли, какое количество параллельных ветвей будет подключено – на каждой из них напряжение будет одно и то же. Как же получить выражение для тока I? Начнем рассуждать с того, что мощность, отдаваемая источником должна быть равна мощности, потребляемой нагрузкой, ведь закон сохранения энергии никто не отменял. Запишем выражения для мощностей, пренебрегая внутренним сопротивлением источника:Pист=I∙εPнагр=PR1+PR2=I1∙UR1+I2∙UR2=I1∙ε+I2∙ε=(I1+I2)∙εПриравнивая правые части уравнений, получим:
Учитывается именно алгебраическая сумма (с учетом знака), потому что направление тока мы можем положить любым, ведь в сложной схеме можем заранее не знать, втекает ток в узел или вытекает из него (втекающий ток берётся со знаком «плюс», вытекающий – со знаком «минус»). То есть мы, например, могли бы перенести слагаемое I в правую часть и получили бы уравнение, в котором втекающие токи были бы со знаком «минус», а вытекающие со знаком «плюс», но ничего не мешает нам поделить обе части уравнения на -1. Это утверждение называется I правило Кирхгофа или правило токов Кирхгофа. Иногда его не совсем корректно называют законом Кирхгофа. Всё-таки это правило, потому что оно не является фундаментальным законом природы, а вытекает из других фундаментальных законов.
Закон Ома является частным случаем II правила Кирхгофа для цепи из одного контура. Здесь выражение «алгебраическая сумма» значит, ровно то же, что и для I правила, только для напряжений.Как использовать эти правила для расчета сложных электрических цепей мы рассмотрим на следующем уроке, который полностью будет посвящен практике.
При подобной замене мы будем пользоваться следующим вариантом записи:
Пришло время запоминать еще одно важное правило: величина, обратная общему сопротивлению параллельных ветвей, равна сумме величин, обратных сопротивлениям каждой ветви
Или, иначе: эквивалентная проводимость параллельных ветвей равна сумме проводимостей этих ветвей.
Немного тавтологии, пожалуй, не помешает…
Посмотрим, что произойдёт, если мы заменим эквивалентное сопротивление двумя одинаковыми параллельно включенными сопротивлениями (рисунок 8.3). Чтобы сохранить величину эквивалентного сопротивления равным 1Ом, рассчитаем величины сопротивлений R1 и R2:
то есть каждое из сопротивлений должно быть больше эквивалентного в 2 раза.Рассчитаем мощность, выделяемую на каждом из этих сопротивлений:
Суммарная мощность нагрузки осталась прежней, однако, как нам уже известно, мощность выделяемая на сопротивлении, полностью переходит в тепло, следовательно, при одной и той же рассеиваемой мощности, во втором случае мы получим более комфортный температурный режим для нагрузки (температура каждого сопротивления будет ниже, чем температура эквивалентного сопротивления) за счет увеличения в 2 раза площади рассеивания (ведь мы используем два проводника вместо одного). Соответственно, трата дополнительных денег на приобретение двух проводников позволяет нам сэкономить на охлаждении. Часто бывают такие ситуации, что слишком большой перегрев элемента может приводить к выходу его из строя (даже такой простой вещи как кусок проводника). Кроме того, многие полупроводниковые приборы (диод, транзистор, тиристор) рассчитаны на определенный номинальный ток, и, чтобы увеличить предел номинального тока, такие приборы включают параллельно. Можно, конечно, взять прибор с большим номинальным током, но чаще всего стоимость таких прибор намного больше. Экономия, однако…
тогда, подставляя значение тока в выражение для падения напряжения, получим:
Из полученных соотношений видно, что величина падения напряжения зависит от эдс источника и соотношения сопротивлений.
При R1=R2 падение напряжения на каждом сопротивлении составит ровно половину эдс источника. Таким образом мы поделили напряжение пополам и теперь можем использовать отвод в точке А в качестве «плюса» своеобразного источника питания, но с пониженным напряжением. Такая схема называется делителем напряжения. Ее полезно применять, когда имеется источник с большим напряжением, чем требуется. Сопротивление R1 называется верхним плечом, а сопротивление R2 – нижним. Однако, резистивный делитель напряжения обладает существенными недостатками: во-первых, потери мощности на плечах делителя снижают кпд устройства, поскольку просто переходят в тепло, а, во-вторых, сопротивление выходного плеча (с которого снимается часть эдс) должно быть согласовано с сопротивлением нагрузки, чтобы сохранять требуемое напряжение. Рассмотрим эти два момента на примере общего случая включения сопротивлений так называемого смешанного соединения.
Однако, нам неизвестны токи I1 и I2, так же как и сопротивления R1 и R2. В таких случаях при разработке схемы необходимо самому задать необходимые недостающие условия, но так, чтобы задача имела решение. Например, мы могли бы задать R1=10 Ом, но ведь ток I1 не может быть менее 4А, а значит:UR1>I1∙R1=4А∙10Ом=40В,что заведомо больше, чем напряжение на аккумуляторе. Чтобы не угадывать значения сопротивлений, давайте для уменьшения потерь на сопротивлении R2 зададим ток I2 равным 10% от тока нагрузки, ведь ничто не мешает нам так сделать.
Ток I1 можно рассчитать двумя способами:
Заметьте, что эквивалентное сопротивление всегда меньше меньшего сопротивления!Ток I1 соответствует току через последовательное соединение сопротивлений R1 и Rэкв. Его можно найти из закона Ома:
Теперь рассчитаем этот же ток, используя первый способ:
Итак, при помощи двух сопротивлений мы спроектировали (ого-го!) устройство понижения напряжения с 12 В до 5 В. Давайте оценим кпд этого устройства. Полезной мощностью у нас является мощность нагрузки Pн=20 Вт, а полной мощностью – мощность, отдаваемая аккумуляторной батареей, которая равна произведению потребляемого тока (I1) на эдс батареи:
Всего-то! Ужасно! Давайте подумаем, как можно увеличить этот показатель…Но сначала разберемся откуда берутся такие большие потери мощности… А браться им, кроме как на нагрев сопротивлений R1 и R2 неоткуда. Давайте рассчитаем мощность потерь для каждого из них:
Потери мощности на нем:
Кпд вырос, но потери все равно огромные! Но больше мы сделать, к сожалению ничего не можем: такая схема попросту неэффективна… Мы впустую потратили больше энергии, чем получили полезной работы. Вот такой первый недостаток схемы делителя напряжения.
Посмотрим, что произойдет с напряжением на нижнем плече делителя, то есть на нагрузке:
В сумме напряжения на плечах делителя равны эдс источника, значит:
Тогда нагрузке достанется часть эдс, равная:
