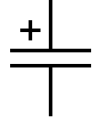5. Цепь переменного тока с разной нагрузкой. Активная нагрузка в цепи переменного тока3.2 Виды нагрузок в цепи переменного токаа) Активное сопротивление в цепи переменного тока. Рассмотрим цепь переменного тока, в которую включен только резистор сопротивлениемR не обладающий ни индуктивностью, ни ёмкостью (рис.5а). Такая нагрузка называется активной. Единственным результатом прохождения тока в этом случае будет превращение в резисторе энергии электрического тока в тепловую энергию. В этом случае ток через резистор будет определяться законом Ома i = I0sinωt, а напряжение на резисторе – u = I0R·sinωt = U0sinωt. Т.е. ток и напряжение совпадают по фазе. График тока и напряжения, а также векторная диаграмма амплитуд тока и напряжения показаны на рис. 5б и 5в. б) Индуктивное сопротивление в цепи переменного тока. Рассмотрим случай, когда цепь переменного тока содержит только катушку индуктивностью L, ёмкостью С = 0 и с активным сопротивлением R = 0 (рис.6а). Переменное напряжение u = U0cosωt, поданное на концы катушки, вызовет переменный ток. В результате этого возникнет ЭДС самоиндукции , которая в любой момент времени противоположна по направлению и равна по величине, приложенному к катушке напряжениюuL = U0cosωt: . Теперь закон Ома, для рассматриваемого участка примет вид: U0cosωt = 0,откуда = U0cosωt и di = cosωtdt. После интегрирования для тока получим: i = sinωt + const. Очевидно, что постоянная составляющая тока отсутствует, т.е. const = 0. Теперь i = sinωt = cos(ωt – 900) = I0 cos(ωt – 900). Откуда следует, что , где- индуктивное сопротивление катушки. Оно увеличивается с ростом частоты переменного тока. . Как видно из волновой и векторной диаграмм (рис.6 б,в), в цепи с чисто индуктивным сопротивлением, ток в катушке отстаёт по фазе от напряжения на π/2 радиан. в) Емкостное сопротивление в цепи переменного тока. Рассмотрим случай, когда в цепь включен только конденсатор С (рис.7а) Сопротивление и индуктивность подводящих проводов примем равными нулю. Мгновенное значение напряжения на конденсаторе можно выразить формулойuс=q/C, гдеq– величина заряда на обкладках конденсатора в данный момент времени. Так как всё внешнее напряжениеu=U0cosωtприложено к конденсатору тоuс ==U0cosωt. Откуда q =CU0cosωt. Производная от q поtдаёт силу токаiв цепи:i== – ωCU0sinωt=I0cos(ωt+ 900), гдеI0 = ωCU0= – амплитудное значение силы тока в цепи. Отсюда видно, что выражениеопределяет сопротивление, которое оказывает переменному току конденсатор. Ёмкостное сопротивление уменьшается с ростом частоты. [ХC] = Ом. В цепи с чисто емкостным сопротивлением напряжение, приложенное к обкладкам конденсатора, отстаёт по фазе от тока на π/2 радиан. Это показано на волновой и векторной диаграммах (рис.7 б, в). 4.Импеданс цепи переменного тока с последовательным включением резистора, катушки и конденсатора. Резонанс напряженийРассмотрим цепь, состоящую из резистораR, катушки индуктивности L и конденсатора C (рис.7а). Подадим на концы этой цепи переменное напряжение u = U0cosωt. В цепи возникнет переменный ток той же частоты ω, амплитудой I0и фазой φ, значение которой будет определяться параметрами цепи: сопротивлениемR, индуктивностью L и электроёмкостью С. Этот ток вызовет падения напряжений на отдельных элементах участка цепи – U0,R,U0,C,U0,L.Поскольку соединение последовательное, то результирующее напряжениеU0 будет определяться векторной суммой напряжений на отдельных элементах (рис.7б). По теореме Пифагора получим: . (14) Закон Ома для данной цепи запишется так: , (15) где – полное сопротивление или импеданс цепи переменного тока. Треугольник сопротивлений представлен на рис. 8. Разность фаз между токомI и напряжением U определяется углом φ между векторами U0 и I0. Из диаграммы (рис.8) следует: . (16) Из формулы для Z вытекает, что чем ближе по величине и 1/ωС, тем меньше полное сопротивлениеZ и тем больше ток в цепи. При ωL = 1/ωC угол сдвига фаз обращается в нуль (φ = 0), полное сопротивление Z = R и ток достигает максимального значения: I0,max = U0,рез/ R. (17) Это явление называется резонансом напряжения. Для цепи с заданными L и C, резонанс имеет место при частоте . РАБОТА И МОЩНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА Мгновенное значение мощности р(t) переменного тока равно произведению мгновенных значений напряжения u(t) =U0cosωtи силы токаi(t) = I0cos(ωt– φ): р(t) = U0cosωtI0 cos(ωt – 900) = I0U0 cosωt cos(ωt – 900).() Воспользовавшись формулой получим: . Практический интерес представляет среднее по времени значение мощности Р. Т.к. среднее значение cos(2ωt- φ) равно нулю, то .() Из векторной диаграммы рис. 7б следует, что U0 cosφ= RI0. Поэтому. Такую же мощность развивает постоянный ток, силой. Это значение называется действующим (или эффективным) значением силы переменного тока. Аналогично величинаназывается действующим (или эффективным) значением напряжения. С использованием действующих (или эффективных) значений тока и напряжения Р =U0 I0cosφ.Множительcosφназывается коэффициентом мощности. Как видно из диаграммы рис. 7б, при равенстве реактивных значений сопротивлений ХC= ХLмножительcosφ= 1 (φ = 0) Р =U0 I0, т.е. выделяющаяся в цепи мощность имеет максимальное значение. При чисто реактивном сопротивлении цепи (R= 0) мощность, выделяемая в цепи, равна нулю. По этой причине на практике электрическую цепь переменного тока стремятся сбалансировать так чтобы значения реактивных сопротивлений ХCи ХLбыли как можно ближе. Для промышленных установок наименьшее допустимое значениеcosφ= 0,85. или. (48) Работа за период T: . (49) Средняя мощность переменного тока . (50) Обозначим , откуда эффективный (действующий) ток -.(51) Тогда . (52) Из сравнения соотношений (47) и (52) следует, что эффективная сила переменного равна силе такого постоянного тока, который имеет ту же мощность, что и данный переменный ток. Если в цепи переменного тока имеются реактивные сопротивления, то мощность: (53) (на основании тригонометрического тождества: ). Среднее значение мощности NСза период Т, а, следовательно, и за любой промежуток времениt>>T, равно разности средних значений. Но первый член есть постоянная величина, не зависящая от времени, а второй – периодическая функция, среднее значение которой за периодTравна нулю. Таким образом,(54) или (55) Множитель называется коэффициентом мощности электрической цепи. ЕслиR=0, тоиNC=0. Энергия, которая поступает в цепь от источника за T/2, возвращается источнику в течение следующей половины периода. Следовательно, для повышения мощности, отдаваемой переменным током в цепь, необходимо добиться повышенияпутём включения в цепь такихRLиRCнагрузок, которые соответствуют условию резонанса (45). ПРИРОДА ЕМКОСТНЫХ СВОЙСТВ ТКАНЕЙ ОРГАНИЗМА studfiles.net 5. Цепь переменного тока с разной нагрузкойЦепь переменного тока с активно-индуктивной нагрузкой Рассмотрим электрическую цепь (рис. 9), в котором через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток: I = I0 sin ωt (1.23) Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе: U = UL+UR (1.24) Напряжение на резисторе, как показано выше, совпадает по фазе с током: UR = U0R sin ωt (1.25) а напряжение на индуктивности равно ЭДС самоиндукции со знаком “минус” (по второму правилу Кирхгофа): UL = L(dI/dt)= I0 ωLcos ωt = U0Lsin(ωt + π/2) (1.26) где U0L= I0 ωL (1.27) Напряжение на индуктивности опережает ток на π/2. Переходя к формуле (1.27) к действующим значениям переменного тока (I = I0/√2; U= U0/√2), получим: I = UL/XL (1.28) Это закон Ома для цепи с идеальной индуктивностью (т.е. не обладающей активным сопротивлением), а величина XL= ωL называется индуктивным сопротивлением. Построив векторы I, UR и UL и воспользовавшись формулой (1.24), мы найдем вектор U. Как видно из векторной диаграммы, модуль вектора U равен U= √ UR + UL = √ I R + I (ωL) = I√ R + (ωL) = IZ (1.29) где величина Z = √ R + (ωL) (1.30) называется полным сопротивлением цепи. Сдвиг по фазе φ между током и напряжением также определяется из векторной диаграммы: tg φ = UL/ UR = ωL/ R (1.31) В данной цепи угол сдвига фаз между током и напряжением зависит от значений R и L и изменяется в пределах от 0 до π/2. Теперь рассмотрим как изменяется со временем мощность в цепи с активно-индуктивной нагрузкой. Мгновенные значения тока и напряжения можно представить в виде: U(t) = U0 sin ωt (1.32) I(t) = I0 sin(ωt − φ) Тогда мгновенное значение мощности равно: p(t)= I(t) U(t) = I0 U0 sin ωt sin(ωt − φ)=(I0 U0/2)[cosφ − cos(2ωt − φ)] = =(I0 U0/2)(1− cos2ωt) cosφ − (I0 U0/2) sin2ωt sin φ (1.33) Мгновенное значение мощности имеет две составляющие: первое слагаемое — активная, и второе — реактивная (индуктивная). Поэтому средняя за период мощность не равна нулю: T T T Pср = 1/T ∫ pdt = (I0 U0/2T) cosφ ∫dt − (I0 U0/2T) cosφ ∫ cos2ωt dt − 0 0 0 T −(I0 U0/2T) sin φ ∫ sin2ωt dt = (I0 U0/2) cosφ (1.34) 0 и является активной мощностью. Соответствующая этой мощности электрическая энергия превращается в активном сопротивлении R в теплоту. Цепь переменного тока с емкостью Рассмотрим электрическую цепь, в которой переменное напряжение (1.11) приложено к емкости С (рис. 11). Мгновенное значение тока в цепи с емкостью равно скорости заряда на обкладках конденсатора: I = dq/dt (1.35) но, т.к. q = CU, то I = C (dU/dt) = ωCU0 cos ωt = I0 sin (ωt + π/2) (1.36) где ωCU0 = I0 (1.37) В этой цепи ток опережает напряжение на π/2. Переходя в формуле (1.37) к действующим значениям переменного тока (I = I0/√2; U= U0/√2), получим: I0 = U/Xc (1.38) Это закон Ома для цепи переменного тока с емкостью, а величина Xc= 1/ωC называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 12. Найдем мгновенную и среднюю мощность в цепи, содержащей емкость. Мгновенная мощность равна: p(t)= i(t) u(t) = I0U0 sin (ωt + π/2) sin ωt = IUsin2 ωt (1.39) Мгновенная мощность изменяется с удвоенной частотой (рис. 13). При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные — его разряду и возврату запасенной энергии в источник. Средняя за период мощность здесь равна нулю T T Pср = 1/T ∫ p(t)dt = IU/T ∫ sin2 ωt dt = 0 (1.40) 0 0 т.к. в цепи с конденсатором активная мощность не потребляется, а проходит обмен электрической энергией между конденсатором и источником. Цепь переменного тока с активно-емкостной нагрузкой Реальная цепь переменного тока с емкостью всегда содержит активное сопротивление — сопротивление проводов, активные потери в конденсаторе и т.п. Рассмотрим реальную цепь, состоящую из последовательно соединенных конденсатора С и активного сопротивления R (рис. 14). В этой цепи протекает ток I = I0 sin ωt . В соответствии со вторым правилом Кирхгофа, сумма напряжений на резисторе и на емкости равна приложенному напряжению: U = UR + UC (1.41) Напряжение на резисторе совпадает по фазе с током: UR = U0R sin ωt (1.42) а напряжение на конденсаторе отстает от тока: UC = U0C sin (ωt − π/2) (1.43) Построив векторы I,UR и UC и воспользовавшись формулой (1.41), найдем вектор U. Векторная диаграмма для этой цепи показана на рисунке 15. Как видно из векторной диаграммы, модуль вектора U равен U =√ UR + UC =√ I R + I (1/ωC) = I √ R + (1/ωC) = IZ1 (1.44) где величина Z1=√ R + (1/ωC) (1.45) называется полным сопротивлением цепи. Сдвиг по фазе φ между током и напряжением в данной цепи также определяется из векторной диаграммы: tg φ = UC/ UR = (1/ωC)/ R (1.46) В рассмотренной цепи угол сдвига фаз между током и напряжением зависит от значений R и C и изменяется в пределах от 0 до π/2. Рассмотрим теперь, как изменяется со временем мощность в цепи с активно – емкостной нагрузкой. Мгновенные значения тока и напряжения можно представить в виде: U (t) = U0 sin ωt I (t) = I0 sin (ωt + φ) (1.47) Тогда мгновенное значение мощности равно: p(t)= I(t) U(t) = I0 U0 sin ωt sin(ωt + φ)=(I0 U0/2)[cosφ − cos(2ωt + φ)] = =(I0 U0/2)(1− cos2ωt) cosφ + (I0 U0/2) sin2ωt sin φ (1.48) Мгновенное значение мощности имеет две составляющие: первое слагаемое — активная, а второе — реактивная (емкостная). Поэтому средняя за период мощность не равна нулю: T T T Pср =1/T ∫ pdt = I0U0/2T cosφ ∫ dt − I0U0/2T cosφ ∫ cos2 ωtdt + I0U0/2T ∙ 0 0 0 T sin φ ∫ sin2ωt dt = I0U0/2T cosφ (1.49) 0 и является активной мощностью. Соответствующая этой мощности электрическая энергия превращается в активном сопротивлении R в теплоту. studfiles.net ВИДЫ НАГРУЗОК В ЦЕПИ ПЕРЕМЕННОГО ТОКАКоличество просмотров публикации ВИДЫ НАГРУЗОК В ЦЕПИ ПЕРЕМЕННОГО ТОКА - 296
а)Активное сопротивление в цепи переменного тока. Рассмотрим цепь переменного тока, в которую включен только резистор сопротивлением R не обладающий ни индуктивностью, ни ёмкостью (рис.5а). Такая нагрузка принято называть активной. Единственным результатом прохождения тока в данном случае будет превращение в резисторе энергии электрического тока в тепловую энергию. В этом случае ток через резистор будет определяться законом Ома i = I0sinωt, а напряжение на резисторе – u = I0R·sinωt = U0sinωt. Т.е. ток и напряжение совпадают по фазе. График тока и напряжения, а также векторная диаграмма амплитуд тока и напряжения показаны на рис. 5б и 5в. б)Индуктивное сопротивление в цепи переменного тока. Рассмотрим случай, когда цепь переменного тока содержит только катушку индуктивностью L, ёмкостью С = 0 и с активным сопротивлением R = 0 (рис.6а). Переменное напряжение u = U0cosωt, поданное на концы катушки, вызовет переменный ток. В результате этого возникнет ЭДС самоиндукции , которая в любой момент времени противоположна по направлению и равна по величине, приложенному к катушке напряжению uL = U0cosωt: . Теперь закон Ома, для рассматриваемого участка примет вид: U0cosωt= 0, откуда = U0cosωt и di = cosωt×dt. После интегрирования для тока получим: i = ×sinωt + const. Очевидно, что постоянная составляющая тока отсутствует, ᴛ.ᴇ. const = 0. Теперь i = ×sinωt = ×cos(ωt – 900) = I0 cos(ωt – 900). Откуда следует, что , где - индуктивное сопротивление катушки. Оно увеличивается с ростом частоты переменного тока. . Как видно из волновой и векторной диаграмм (рис.6 б,в), в цепи с чисто индуктивным сопротивлением, ток в катушке отстаёт по фазе от напряжения на π/2 радиан. в) Емкостное сопротивление в цепи переменного тока. Рассмотрим случай, когда в цепь включен только конденсатор С (рис.7а) Сопротивление и индуктивность подводящих проводов примем равными нулю. Мгновенное значение напряжения на конденсаторе можно выразить формулой uс = q / C, где q – величина заряда на обкладках конденсатора в данный момент времени. Так как всё внешнее напряжение u = U0cosωt приложено к конденсатору то uс = = U0×cosωt. Откуда q = C×U0×cosωt. Производная от q по t даёт силу тока i в цепи: i = = – ωCU0 sinωt = I0 cos(ωt + 900), где I0 = ωCU0 = – амплитудное значение силы тока в цепи. Отсюда видно, что выражение определяет сопротивление, ĸᴏᴛᴏᴩᴏᴇ оказывает переменному току конденсатор. Размещено на реф.рфЁмкостное сопротивление уменьшается с ростом частоты. [ХC] = Ом. В цепи с чисто емкостным сопротивлением напряжение, приложенное к обкладкам конденсатора, отстаёт по фазе от тока на π/2 радиан. Это показано на волновой и векторной диаграммах (рис.7 б, в). referatwork.ru 2.4. Нагрузки в цепях переменного токаАктивное сопротивление ( r) – нагрузка, аналогичная той, которая использовалась в цепях постоянного тока. Реактивные сопротивления (X) – нагрузки, которые не использовались в цепях постоянного тока. Они используются только в цепях переменного тока и не потребляют активную мощность.
|
|
||||||||||||||||||
|
|
||||||||||||||||||
|




 Индуктивность
Индуктивность , где
, где  .
. , и индуктивность, как коэффициент пропорциональности между потокосцеплением и током, равна:
, и индуктивность, как коэффициент пропорциональности между потокосцеплением и током, равна:
 Это определение вытекает из формулы: q = Cu.
Это определение вытекает из формулы: q = Cu. , и аналогичен возникновению напряжения на индуктивности:
, и аналогичен возникновению напряжения на индуктивности: .
. ;
; ;
; .
. . Напряжение на обкладках с учетом поставленных условий равно:
. Напряжение на обкладках с учетом поставленных условий равно: ,
, , а емкость конденсатора:
, а емкость конденсатора:
 Активной нагрузкой в цепи переменного тока называется такой участок, на котором всяэлектрическая энергия необратимопреобразуется в тепловую. В роли активной нагрузки может быть обычный резистор (лампа накаливания, электронагревательный элемент и т.д.)
Активной нагрузкой в цепи переменного тока называется такой участок, на котором всяэлектрическая энергия необратимопреобразуется в тепловую. В роли активной нагрузки может быть обычный резистор (лампа накаливания, электронагревательный элемент и т.д.) .
. Чтобы всяэлектрическая энергия необратимо преобразовывалась в тепловую энергию, необходимо, чтобы мгновенная мощность в любой момент времени была положительной, а это возможно только при
Чтобы всяэлектрическая энергия необратимо преобразовывалась в тепловую энергию, необходимо, чтобы мгновенная мощность в любой момент времени была положительной, а это возможно только при  . Следовательно, для активной нагрузки напряжение и сила тока колеблются в одной фазе.
. Следовательно, для активной нагрузки напряжение и сила тока колеблются в одной фазе.
 и напряжения
и напряжения  пропорциональны друг другу. Это утверждение – не что иное, как закон Ома для участка цепи:
пропорциональны друг другу. Это утверждение – не что иное, как закон Ома для участка цепи:
 Таким образом, на активной нагрузке закон Ома выполняется как для мгновенных, так и для амплитудных значений.
Таким образом, на активной нагрузке закон Ома выполняется как для мгновенных, так и для амплитудных значений. Тепло, выделяемое в резисторе при протекании по нему постоянного тока, может быть найдено из закона Джоуля –Ленца:
Тепло, выделяемое в резисторе при протекании по нему постоянного тока, может быть найдено из закона Джоуля –Ленца:
 , выделяемое переменным током в том же сопротивлении R за малое время
, выделяемое переменным током в том же сопротивлении R за малое время  , может быть выражено через мгновенное значение тока
, может быть выражено через мгновенное значение тока  :
:
 Тепло, выделяемое за период, находим суммированием малых
Тепло, выделяемое за период, находим суммированием малых 
 Приравняв (*) и (**), найдем действующее значение переменного тока:
Приравняв (*) и (**), найдем действующее значение переменного тока: Выражения для действующих значений ЭДС и напряжения выглядят аналогично:
Выражения для действующих значений ЭДС и напряжения выглядят аналогично: 5. Емкостная нагрузка в цепи переменного тока.
5. Емкостная нагрузка в цепи переменного тока.  .
. . Тогда заряд на конденсаторе
. Тогда заряд на конденсаторе


 .
.

 Величина, стоящая перед знаком косинуса, - амплитудное значение тока
Величина, стоящая перед знаком косинуса, - амплитудное значение тока - проводимость участка цепи, содержащего конденсатор. Тогда величина
- проводимость участка цепи, содержащего конденсатор. Тогда величина  играет роль сопротивления, его называют емкостным сопротивлением.
играет роль сопротивления, его называют емкостным сопротивлением. .С увеличением частоты тока сопротивление конденсатора падает, а амплитуда тока при этом, наоборот, увеличивается. Таким образом, конденсатор хорошо «пропускает» ток высокой частоты и плохо – низкой. Сопротивление конденсатора становится бесконечно большим, если частота тока
.С увеличением частоты тока сопротивление конденсатора падает, а амплитуда тока при этом, наоборот, увеличивается. Таким образом, конденсатор хорошо «пропускает» ток высокой частоты и плохо – низкой. Сопротивление конденсатора становится бесконечно большим, если частота тока  , то есть постоянный ток не может течь через участок, содержащий конденсатор (как это уже было сказано ранее).
, то есть постоянный ток не может течь через участок, содержащий конденсатор (как это уже было сказано ранее).
 , следовательно, участок цепи, содержащий конденсатор, не потребляет энергию от сети. Точнее, мгновенная мощность в цепи с конденсатором меняет знак через каждые четверть периода. Четверть периода конденсатор заряжается, потребляя энергию от источника, на этом этапе мгновенная мощность положительна. Следующую четверть периода конденсатор разряжается, возвращая энергию источнику, при этом мгновенная мощность отрицательна.
, следовательно, участок цепи, содержащий конденсатор, не потребляет энергию от сети. Точнее, мгновенная мощность в цепи с конденсатором меняет знак через каждые четверть периода. Четверть периода конденсатор заряжается, потребляя энергию от источника, на этом этапе мгновенная мощность положительна. Следующую четверть периода конденсатор разряжается, возвращая энергию источнику, при этом мгновенная мощность отрицательна.