Расчет тока в цепи переменного тока: Расчет цепей переменного тока

Расчет цепей переменного тока

Расчет
электрических цепей переменного
синусоидального тока производится в
комплексной форме. При этом величины
синусоидальных ЭДС и токов представляются
в виде комплексных амплитуд или
комплексных действующих значений, а
все элементы в схеме – в виде комплексных
сопротивлений.

Например,
если ЭДС источника равна
,
то комплексная амплитуда запишется в
виде- в показательной форме записи, или- в алгебраической форме. Комплексное
действующее значение синусоидальной
ЭДС:- в показательной форме записи, или- в алгебраической форме.

Комплексные
сопротивления элементов электрической
цепи переменного тока:

— для идеального сопротивления,

— для идеальной индуктивности,

— для идеальной емкости.

Далее
расчет электрической цепи переменного
тока можно вести любым методом, известным
из раздела – «электрические цепи
постоянного тока». При этом используется
математический аппарат, разработанный
для операций с комплексными числами.

Применяются
три формы записи комплексного значения
синусоидальной величины:

— показательная форма,

— алгебраическая форма,

где
и- действительная и мнимая часть
комплексного значения синусоидальной
величины. Переход от алгебраической
формы к показательной осуществляется
по формулам:

;.

Переход
от показательной формы к тригонометрической
осуществляется по формуле Эйлера:

.

Сложение
и вычитание комплексных величин
производится в алгебраической форме,
а умножение и деление в показательной.

При
анализе цепей синусоидального тока
применяют главным образом комплексные
действующие значения синусоидальных
величин, сокращенно их называют
комплексными значениями.

Расчет
однофазных цепей переменного тока при
наличии одного источника синусоидальной
ЭДС производится методом эквивалентных
преобразований. Рассмотрим пример
расчета однофазной цепи приведенной
на рис.

Рис. 2.4. Схема электрической цепи к
примеру расчета

Пример
расчета однофазной цепи

По
заданным значениям активных и реактивных
сопротивлений и напряжению источника
определить токи во всех ветвях схемы и
падения напряжения на ее участках.
Определить комплекс полной мощности,
активную и реактивную мощность. Расчет
произвести комплексным методом. Выполнить
проверку правильности расчета с
использованием баланса активных
мощностей схемы. Построить векторную
диаграмму. Построить мгновенные значения
синусоидальных токов ветвей. Исходные
данные для расчета приведены в таблице.

U, В	R1, Ом	R2, Ом	R3, Ом	X1, Ом	X2, Ом	X3, Ом
100	50	100	100	50	50	100

Решение:

Электрическая
цепь на рис. 2.4 состоит из трех ветвей,
определим комплексные сопротивления
ветвей. Сопротивление первой ветви,
состоящей из сопротивления R1
и идеальной катушки индуктивности с
комплексным сопротивлением:

Ом.

Сопротивление
второй ветви, состоящей из сопротивления
R2 и идеальной емкости с
комплексным сопротивлением:

Ом.

Сопротивление
третьей ветви, состоящей из сопротивления
R3 и идеальной катушки
индуктивности с комплексным сопротивлением:

Ом.

Вторая
и третья ветвь соединены параллельно,
поэтому их эквивалентное сопротивление

Эквивалентное
сопротивление всей схемы:

Ом.

Зная
эквивалентное сопротивление, можно
определить ток в первой ветви:

А.

Затем
можно определить напряжения на участках
цепи:

В,

В.

Зная
напряжение на участке bc можно рассчитать
токи

А,

А.

Проверку
правильности расчета токов можно
выполнить по первому закону Кирхгофа
в комплексной форме:

,
или

.

Так
как первый закон Кирхгофа выполняется,
значит, расчет токов выполнен верно.

Комплекс
полной мощности:

,

где
—
сопряженный комплекс тока.
ЕслиА, то сопряженный комплексА.
Таким образом, комплекс полной мощности
равен

ВА.

При
этом действительная часть комплекса
полной мощности равна активной мощности
потребляемой схемой

Вт,

а мнимая
часть комплекса полной мощности равна
реактивной мощности схемы

ВА.

Векторная
диаграмма токов и напряжений строиться
на комплексной плоскости по координатам,
полученным при расчете в комплексной
форме. Токи и напряжения строятся в
одних координатных осях, но для них
выбираются разные масштабы. Диаграмма
для рассчитанной схемы показана на рис.
2.5.

Рис. 2.5. Векторная диаграмма токов и
напряжений

Выражения для
мгновенных значений токов можно получить
из комплексных значений записанных в
показательной форме:

А.

Действующее
значение тока I1 = 0.724 А, а
фазовый сдвиг,
таким образом мгновенное значение тока
равно

А.

Аналогично для
остальных токов:

А.

А.

А.

А.

Графики мгновенных
значений токов приведены на рис. 2.6.

Рис.
2.6. Мгновенные значения токов

Расчет простых цепей постоянного тока

ТОЭ расчеты

В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.  

Пример 1

  Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов  R₁ = 20 и R₂ = 32 Ом. Определить ток в цепи и напряжения на резисторах.

 

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи. 

Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов. 

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. 

Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.

В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. 

Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.

Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.

Пример 2

  Общий ток цепи, содержащей два соединенных параллельно резистора R₁=70 Ом и R₂=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов. 

Токи в резисторах 

В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.

Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи 

А затем напряжение 

Зная напряжения, найдем токи, протекающие через резисторы 

Как видите, токи получились теми же.

Пример 3

  В электрической цепи, изображенной на схеме R₁=50 Ом, R₂=180 Ом, R₃=220 Ом. Найти мощность, выделяемую на резисторе R₁, ток через резистор R₂, напряжение на резисторе R₃, если известно, что напряжение на зажимах цепи 100 В.

 

Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R₁, необходимо определить ток I₁, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.

Эквивалентное сопротивление и ток в цепи 

Отсюда мощность, выделяемая на R₁ 

Ток I₂ определим с помощью формулы делителя тока, учитывая, что ток I₁ для этого делителя является общим 

Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U₃, как напряжение на резисторе R₂ 

Таким образом производится расчет простых цепей постоянного тока.

Просмотров: 96859

Цепи переменного тока — мощность в зависимости от напряжения и тока

В цепи переменного тока — переменный ток генерируется источником синусоидального напряжения

Напряжение

Токи в цепях с чисто резистивными, емкостными или индуктивными нагрузками.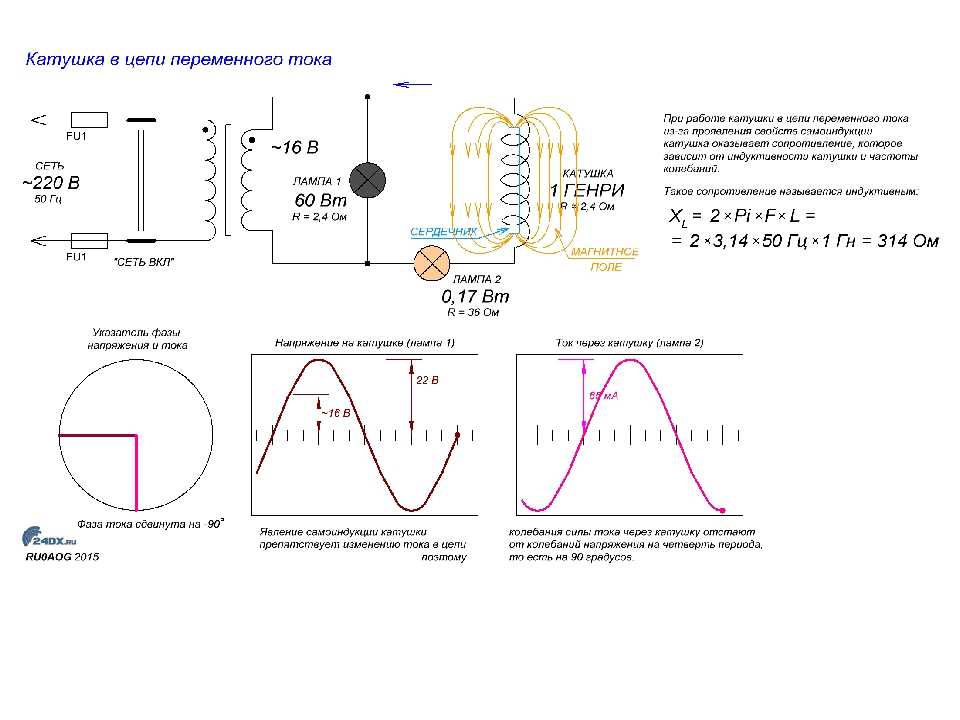

Мгновенное напряжение в синусоидальной цепи переменного тока может быть выражено в виде во временной области как0003

, где

U (T) = напряжение в цепи во время T (V)

U _MAX = максимальное напряжение при амплитуде .

T = Время (S)

ω = 2 π F

= угловая частота синусоидальной волны (RAD/S)

F = частота (Гц, 1/с)

F = частота (Гц, 1/с)

F = частота (Гц, 1/с)

θ = фазовый сдвиг синусоидальной волны (рад)

The momentary voltage can alternatively be expressed in the frequency-domain (or phasor) form as

U = U(jω) = U _max e ^jθ                       (1a)

где

U(jω) = U = комплексное напряжение (В)

Вектор представляет собой комплексное число, выраженное в полярной форме, состоящее из величины, равной пиковой амплитуде синусоидального сигнала, и фазового угла равен фазовому сдвигу синусоидального сигнала относительно косинусоидального сигнала.

Обратите внимание, что конкретная угловая частота — ω — не используется явно в векторном выражении.

Ток

Мгновенный ток может быть выражен во временной области как

i(t) = ток в момент времени t (А)

I _max = максимальный ток при амплитуде синусоидальная волна (А)

Токи в цепях с чистыми резистивными, емкостными или индуктивными нагрузками указаны на рисунке выше. Ток в «реальной» цепи с резистивной, индуктивной и емкостной нагрузкой указан на рисунке ниже.

Мгновенный ток в цепи переменного тока можно альтернативно выразить в частотной области (или векторной форме) как

I = I(jω) = I _MAX E ^Jθ (2A)

, где

I = I (Jω) = Комплекс. Системы переменного тока являются фиксированными — например, 60 Гц в Северной Америке и 50 Гц в большей части остального мира.

Угловая частота для Северной Америки

ω = 2 π 60

= 377 RAD/S

Угловая частота для большей части остального мира составляет

ω = 2 π 50

= 314 RAD/S

Устойчивая нагрузка

Напряжение на резистивную нагрузку в системе переменного тока может быть выражено как

U = R I (4)

, где

R = сопротивление (OHM)

Для нагрузки сопротивления в цепи переменного тока. в фазе с током.

Индуктивная нагрузка

Напряжение на индуктивной нагрузке в системе переменного тока может быть выражено как

U = J ω L I (5)

, где

l = индуст (Henry) (Henry).

Для индуктивной нагрузки ток в цепи переменного тока равен π/2 (90 ^o ) фаза после напряжение (или напряжение до тока).

емкостная нагрузка

Напряжение на индуктивную нагрузку в системе переменного тока может быть выражено как

U = 1 / (J ω C) I (6)

, где

CI. = емкость (фарад)

Для емкостной нагрузки ток в цепи переменного тока опережает напряжение на π/2 (90 ^o ) фаза .

В реальной электрической цепи присутствует смесь резистивных, емкостных и индуктивных нагрузок со сдвигом фаз напряжение/ток в пределах — π/2 <= φ <=  π/2 , как показано на рисунке ниже.

Ток в «реальной» цепи с резистивной, индуктивной и емкостной нагрузкой . φ — фазовый угол между током и напряжением. где0003

U _z = падение напряжения на нагрузке (вольт, В)

I _z = ток через нагрузку (ампер, А)

Z = полное сопротивление нагрузки, Ом, мс )

Полное сопротивление в цепи переменного тока можно рассматривать как комплексное сопротивление. Импеданс действует как частотно-зависимый резистор, где сопротивление является функцией частоты синусоидального возбуждения.

Полные сопротивления в серии

Результирующее полное сопротивление для последовательных импедансов может быть выражено как

z = z ₁ + z ₂ (7b)

Импедансы в параллельном

Полученный импеданс для импедансов в параллеле может быть выражено как

1 / Z = 1 / Z ₁ + +

1 / Z = 1 / Z ₁ . 1 / Z ₂ (7C)

Доход

Допуск — это перевернутый импеданс

Y = 1 / Z (8)

, где

, где

0019 Y = проводимость (1/Ом)

Среднеквадратичное значение или эффективное напряжение

Среднеквадратичное значение — это эффективное значение синусоидального напряжения или тока.

ОБР — среднее квадрат корня — или эффективное напряжение может быть выражено как

U _ОБРАТА = U _EFF

= U _MAX / (2) ^1/2

/ (2) ^1/2

9002 9 № 9 = № ^1/2

9 № ^1/2

/ (2). 0,707 U _max                   (9)

, где

U _{среднеквадратичные среды} = U _EFF

= среднеквадратичное напряжение (V)

U _MAX 9002 = максимальный уровень.

среднеквадратичный средний средний квадрат — или эффективный ток может быть выражен как

I _{среднеквадратичных средств} = I _EFF

= I _MAX / (2) ^1/2 9 _{/ (2) ^1/2}

        = 0.707 I _max                     (10)

where

I _rms = I _eff

        = RMS current (A)

I _max = максимальный ток (амплитуда) источника синусоидального напряжения (А)

Вольтметры и амперметры переменного тока показывают среднеквадратичное значение напряжения или тока, или 0,707-кратное максимальное пиковое значение. Максимальные пиковые значения в 1,41 раза превышают значения вольтметра.

Пример

• для системы 230 В . U _max = 169 В

Трехфазное напряжение переменного тока — фаза-фаза и фаза-нейтраль

В трехфазной системе переменного тока напряжение может подаваться между линиями и нейтралью (потенциал фазы), или между линиями (линейный потенциал). Результирующие напряжения для двух распространенных систем – европейской 400/230 В и североамериканской 208/120 В для одного периода указаны на рисунках ниже.

400V/230V AC

 

print 400/230V Three Phase Diagram

• L1, L2 and L3 are the three phases line to to neutral potentials — phase potentials
• L1 to L2, L1 to L3 и L2 до L3 — трехфазные межфазные потенциалы — линейные потенциалы
• L2, L2 и L3 — результирующий потенциал трех фаз в симметричной цепи — результирующий потенциал = 0

Модуль линейных потенциалов равен 3 ^1/2 (1,73) модуль фазового потенциала.

U _{RMS, строка} = 1,73 U _{ОБЗА, Фаза} (11)

208V/120 В AC

Печать 208/120 В Три фазового диаграммы

Power

Active -OR or True -True -True -True или True мощность, совершающая фактическую работу в цепи, можно рассчитать как

P = U _ОБЗОР I _ОБЗОР COS φ (12)

, где

P = активная реальная мощность (W)

φ = фазовый угол между током и напряжением (Rad, Degrees)

Cos φ также называется коэффициентом мощности.

Реактивная мощность в цепи может быть рассчитана как0022

Цепи переменного тока

Переменные токи и напряжения имеют синусоидальную форму и изменяются во времени. Переменные токи вызывают другие реакции в резисторах, конденсаторах и катушках индуктивности, чем постоянные токи.

Переменные токи и напряжения

На рисунке 1 показан график зависимости переменного напряжения и переменного тока от времени в цепи, имеющей только резистор и источник переменного тока — генератор переменного тока.

Рисунок 1 Ток и напряжение от источника переменного тока через простой резистор.

Поскольку напряжение и ток достигают своих максимальных значений одновременно, они равны в фазе . Закон Ома и предыдущие выражения для мощности справедливы для этой цепи, если используется среднеквадратичное значение (среднеквадратичное значение) напряжения и среднеквадратичное значение тока, иногда называемое эффективным значением . Эти отношения 

Закон Ома выражается следующим образом: В _R = IR , где В _R — среднеквадратичное напряжение на резисторе, а I — среднеквадратичное значение напряжения в цепи.

Цепи резистор-конденсатор

Цепь с резистором, конденсатором и генератором переменного тока называется 9.0009 RC-цепь . Конденсатор в основном представляет собой набор проводящих пластин, разделенных изолятором; таким образом, постоянный ток не может проходить через конденсатор. Изменяющийся во времени ток может добавлять или снимать заряды с пластин конденсатора. Простая схема зарядки конденсатора показана на рисунке 2.

Рисунок 2 RC-цепь для зарядки конденсатора.

Первоначально, в момент времени t = 0, переключатель (S) разомкнут, и на конденсаторе нет заряда. Когда ключ замкнут, ток будет проходить через резистор и заряжать конденсатор. Ток прекратится, когда падение напряжения на конденсаторе сравняется с потенциалом батареи (В) . Как только конденсатор достигнет максимального заряда, ток уменьшится до нуля. Ток достигает максимума сразу после замыкания ключа и экспоненциально уменьшается со временем. емкостная постоянная времени (τ), греческая буква тау) — это время, за которое заряд уменьшается до 1/ e от его первоначального значения, где e — натуральный логарифм. Конденсатор с большой постоянной времени будет изменяться медленно. Емкостная постоянная времени τ = RC .

Из правил Кирхгофа получаются следующие выражения для разности потенциалов на конденсаторе (V _C ) и тока (I) в цепи: 

, где В — потенциал аккумулятора.

Резистивно-индуктивные цепи

Цепь с резистором, катушкой индуктивности и генератором переменного тока представляет собой RL-цепь .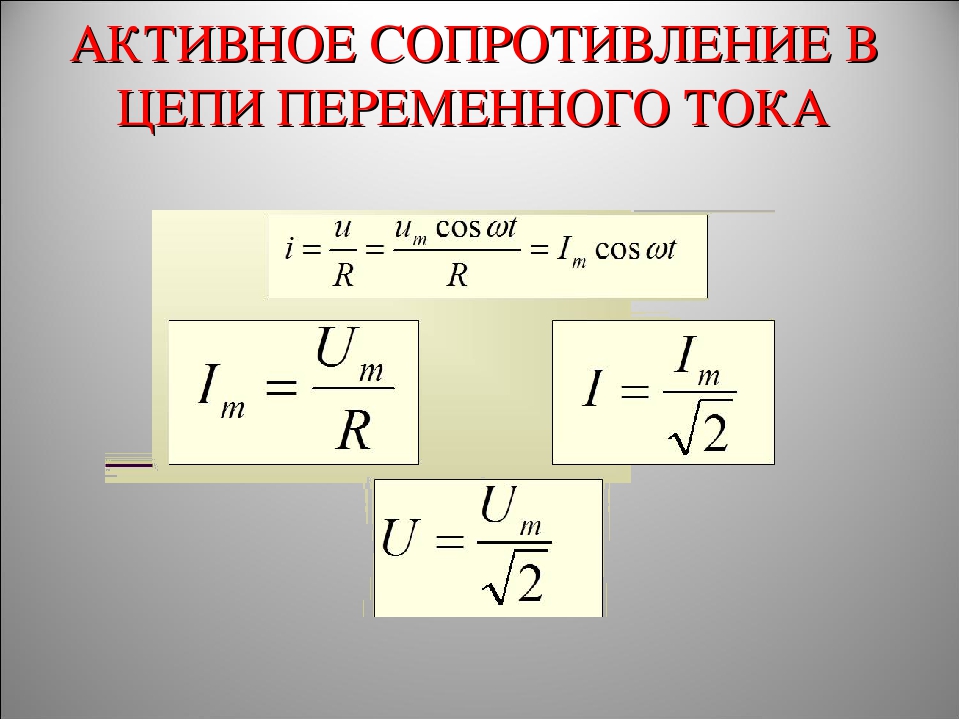 Когда ключ замкнут в цепи RL, в катушке индуктивности индуцируется противо-ЭДС. Следовательно, току требуется время, чтобы достичь своего максимального значения, а постоянная времени, называемая индуктивной постоянной времени , определяется как

Уравнения для тока как функции времени и для потенциала на катушке индуктивности 

В приведенных выше обсуждениях RC- и RL-цепей для простоты использовался переключатель. Размыкание и замыкание переключателя дает реакцию, подобную реакции переменного тока. Цепи RC и RL похожи друг на друга, потому что увеличение напряжения приводит к току, который изменяется экспоненциально в каждой цепи, но в других отношениях реакции различаются. Эти различия в поведении, описанные ниже, приводят к разным откликам в цепях переменного тока.

Реактивное сопротивление

Теперь рассмотрим цепь переменного тока, состоящую только из конденсатора и генератора переменного тока. Графики тока и напряжения на конденсаторе в зависимости от времени показаны на рис.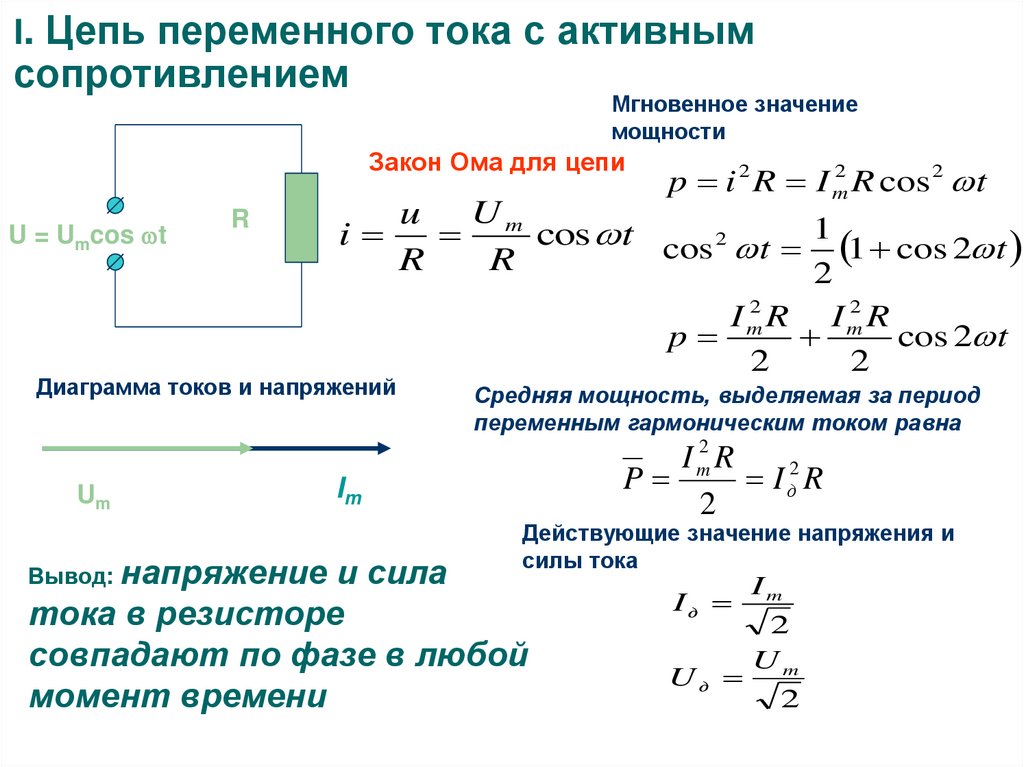 Кривые , а не по фазе, как это было для цепи резистора и генератора переменного тока. (См. рисунок .) Кривые показывают, что для конденсатора напряжение достигает своего максимального значения через одну четверть периода после того, как ток достигает своего максимального значения. Таким образом, напряжение отстает от тока через конденсатор на 90 градусов.

Емкостное сопротивление (X _c ) выражает препятствующее влияние конденсатора на ток и определяется как

Рисунок 3

Ток и напряжение от источника переменного тока через конденсатор.

, где C в фарадах, а частота (f) в герцах. Закон Ома дает В _c = IX _c , где В _c напряжение на конденсаторе0019 I — действующее значение тока в цепи.

Рассмотрим цепь только с катушкой индуктивности и генератором переменного тока. На рисунке показаны графики зависимости тока и напряжения катушки индуктивности от времени. Обратите внимание еще раз, что напряжение и ток не совпадают по фазе. Напряжение для этой цепи достигает своего максимального значения за одну четверть периода до того, как ток достигает своего максимума; таким образом, напряжение опережает ток на 90 градусов.

Рисунок 4 Ток и напряжение от источника переменного тока через индуктор.

Току в цепи препятствует противо-ЭДС катушки индуктивности. Эффективное сопротивление называется индуктивным сопротивлением (X _L ) определяется как (X _L ) = 2π fL , где L измеряется в генри, а f — в герцах. Закон Ома дает (V _L ) = IX _L , где (V _L ) — среднеквадратичное напряжение на дросселе, а I — среднеквадратичное значение напряжения на дросселе.

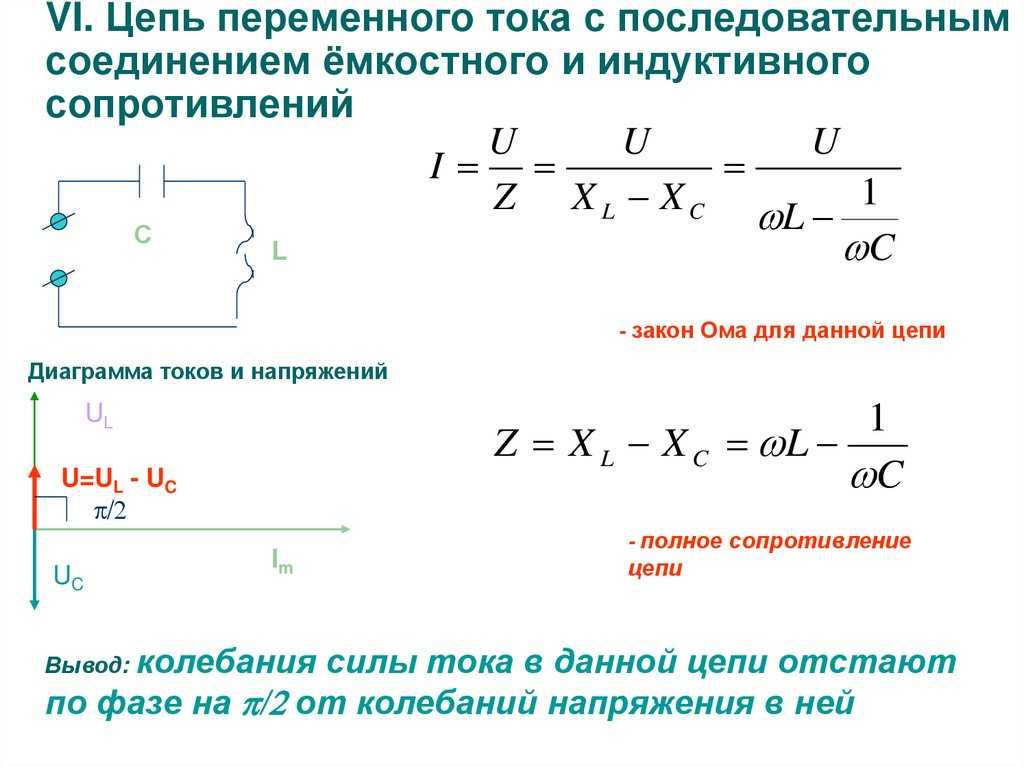
Цепь резистор-индуктор-конденсатор

Цепь с резистором, катушкой индуктивности, конденсатором и генератором переменного тока называется 9.0009 Цепь RLC . Фазовые соотношения этих элементов можно резюмировать следующим образом:

• Мгновенное напряжение на резисторе В _R совпадает по фазе с мгновенным током.

• Мгновенное напряжение на дросселе В _L опережает мгновенный ток на 90 градусов.

• Мгновенное напряжение на конденсаторе В _c отстает от мгновенного тока.

Поскольку напряжения на разных элементах не совпадают по фазе, отдельные напряжения нельзя просто суммировать в цепях переменного тока. Уравнения для полного напряжения и фазового угла равны

.