Содержание
3.5 Расчет режимов сети
Задача
расчета установившихся режимов
электрической сети (нормального для
максимальных и минимальных нагрузок и
послеаварийного) состоит в определении
параметров режима данной сети (напряжений
в узлах, потоков мощности в ветвях схемы,
потерь активной и реактивной мощностей).
Основными исходными данными при расчете
режима сети являются: расчетная схема
сети и параметры схем замещения ее
элементов и расчетные нагрузки узлов
в соответствующих режимах.
Расчет
режимов электрических сетей различных
по структуре производится по соответствующим
математическим моделям (методикам) для
расчета разомкнутых и замкнутых сетей
(с двухсторонним питанием (кольцевых),
сложно замкнутых).
3.5.1
Электрический расчет радиальных и
магистральных участков сети.
Расчет
режимов радиальных и магистральных
участков сети производиться методом
последовательных приближений в два
этапа. На первом этапе определяются
мощности в конце и в начале каждого
участка путем последовательного перехода
от участка к участку в направлении от
конца сети к ее началу с учетом потерь
мощности, которые вычисляются из условия,
что напряжения во всех узлах равны
номинальному напряжению сети.
На
втором этапе расчета по найденным
потокам мощности в начале каждой ветви
определяются потери напряжения в этих
ветвях и напряжения в конце каждой ветви
при последовательном переходе от узла
к узлу в направлении от питающего пункта
до конце участка сети. При расчете сетей
с номинальным напряжением 150 кВ и
ниже можно не учитывать влияние поперечной
составляющей падения напряжения. То
есть принимать за величину потери
напряжения на участке значение продольной
составляющей падения напряжения.
Пример
3.3. Рассчитать
режим участка сети 0-1 для максимальных,
минимальных нагрузок и в послеаварийном
режимах. Напряжение на шинах РЭС при
наибольших нагрузках и в послеаварийном
режимах принять равным 1,1Uн,
а в режиме минимальных нагрузок 1,05Uн.
Расчетная
схема участка приведена на рисунке 3.3
U0
Хл01
RЛ01
U1
0
1
Рисунок 3.
3
Нормальный
режим максимальных нагрузок.
1-й
этап
Принимаем
U1
= Uн
= 110 кВ
Мощность
в конце участка 0-1
(3.14)
Потери
мощности на участке 0-1
(3.15)
Мощность
в начале участка 0-1
(3.16)
2-ой
этап
Определим
напряжение в узле 1 через продольную и
поперечную составляющие падения
напряжения
,
(3.17)
где
продольная и поперечная составляющие
падения напряжения на участке 0-1.
,
(3.18)
,
(3.18)
По
заданию U0=1.1*Uн
= 1,1*110=121 кВ.
Модуль
напряжения в узле 1
В
сетях 150 кВ и ниже поперечной составляющей
падения напряжения можно пренебречь.
Если в рассматриваемом примере учесть
только продольную составляющую падения
напряжения, то модуль напряжения в
первом узле будет
U1
= 121-1,68=119,32 кВ
Как
это видно решения совпадают. Поэтому в
дальнейших расчетах поперечной
составляющей падения напряжения
пренебрегаем.
Для
повышения точности итерационный расчет
можно было бы продолжить. Но для сетей
с номинальным напряжением 150 кВ и ниже
для инженерных расчетом достаточно
одной итерации.
Уточняем
потери мощности
Режим
минимальных нагрузок.
1-й
этап
Принимаем
U1
= Uн
= 110 кВ
Мощность
в конце участка 0-1
Потери
мощности на участке 0-1
Мощность
в начале участка 0-1
2-ой
этап
Определим
напряжение в узле 1 через продольную
составляющие падения напряжения
,
(3.
19)
По
заданию в режиме минимальных нагрузок
U0=1,05*Uн
= 1,05*110=115,5 кВ.
Уточняем
потери мощности
Послеаварийный
режим.
Для
разомкнутых сетей в качестве послеаварийных
режимов рассматриваются режимы отключения
одной цепи всех двухцепных участков.
Поэтому в расчете послеаварийного
режима следует учесть увеличение
активных и реактивных сопротивлений
схем замещения всех двухцепных ЛЭП
вдвое. Сопротивления одноцепных ЛЭП
остаются неизменными.
1-й
этап
Принимаем
U1
= Uн
= 110 кВ
Мощность
в конце участка 0-1
Потери
мощности на участке 0-1
Мощность
в начале участка 0-1
2-ой
этап
Определим
напряжение в узле 1 через продольную
составляющие падения напряжения
По
заданию в послеаварийном режиме U0=1,1Uн
= 1,1*110=121 кВ.
Уточняем
потери мощности
Пример
3.4. Рассчитать
режим участка сети 0-3-4 для максимальных,
минимальных нагрузок и в послеаварийном
режимах. Напряжения на шинах РЭС принять
такими же, как в примере 3.3
Расчетная
схема участка приведена на рисунке 3.4
Рисунок
3.4
Режим
максимальных нагрузок
1-й
этап
Принимаем
U3
=U4
= Uн
= 110 кВ
Мощность
в конце участка 3-4
Потери
мощности на участке 3-4
Мощность
в начале участка 3-4
Мощность
в конце участка 0-3
Потери
мощности на участке 0-3
Мощность
в начале участка 0-3
2-ой
этап
Определим
напряжение в узле 3
,
(3.
20)
Определим
напряжение в узле 4
,
(3.21)
Уточняем
потери мощности
Потери
мощности на участке 3-4
Мощность
в начале участка 3-4
Мощность
в конце участка 0-3
Потери
мощности на участке 0-3
Режим
минимальных нагрузок
1-й
этап
Принимаем
U3
=U4
= Uн
= 110 кВ
Мощность
в конце участка 3-4
Потери
мощности на участке 3-4
Мощность
в начале участка 3-4
Мощность
в конце участка 0-3
Потери
мощности на участке 0-3
Мощность
в начале участка 0-3
2-ой
этап
Определим
напряжение в узле 3
Определим
напряжение в узле 4
Уточняем
потери мощности
Потери
мощности на участке 3-4
Мощность
в начале участка 3-4
Мощность
в конце участка 0-3
Потери
мощности на участке 0-3
Послеаварийный
режим
1-й
этап
Принимаем
U3
=U4
= Uн
= 110 кВ
Мощность
в конце участка 3-4
Потери
мощности на участке 3-4
Мощность
в начале участка 3-4
Мощность
в конце участка 0-3
Потери
мощности на участке 0-3
Мощность
в начале участка 0-3
2-ой
этап
Определим
напряжение в узле 3
Определим
напряжение в узле 4
Уточняем
потери мощности
Потери
мощности на участке 3-4
Мощность
в начале участка 3-4
Мощность
в конце участка 0-3
Потери
мощности на участке 0-3
Расчет
для остальных участков радиально-магистрального
варианта сети выполняем аналогично.
Результаты расчетов сводим в таблицы
3.4 и 3.5.
Таблица
3.4 — Расчетные
величины напряжений на стороне ВН
подстанций
|
№ п/с |
Uвн, |
||
|
Макс. |
Мин. |
ПАР |
|
|
1 |
119,32 |
115,05 |
117,50 |
|
2 |
118,42 |
114,92 |
115,68 |
|
3 |
118,25 |
114,77 |
115,18 |
|
4 |
116,06 |
114,21 |
112,93 |
|
5 |
119,00 |
113,66 |
|
Таблица
3.
5 — Расчетные потери мощности в ЛЭП
|
Участок |
ΔP, |
ΔQ, |
||||
|
Макс |
Мин |
ПАР |
Макс |
Мин |
ПАР |
|
|
0-1 |
0,25 |
0,02 |
0,52 |
0,26 |
0,02 |
0,54 |
|
0-2 |
0,53 |
0,03 |
1,12 |
0,56 |
0,04 |
1,17 |
|
0-3 |
0,53 |
0,05 |
1,13 |
0,56 |
0,05 |
1,19 |
|
3-4 |
0,10 |
0,01 |
0,22 |
0,11 |
0,01 |
0,23 |
|
0-5 |
0,12 |
0,11 |
0,12 |
0,11 |
||
|
Итого: |
1,53 |
0,22 |
2,99 |
1,61 |
0,23 |
3,13 |
Таким
образом, суммарные потери активной и
реактивной мощности в сети в режиме
максимальных нагрузок составляют:
ΔP=1,53 МВт; ΔQ=1,61 Мвар.
3.5.2 Расчет режима
кольцевой сети
Уточненный
расчет режима кольцевой сети в нормальных
режимах производится в два этапа. На
первом этапе производится расчет сети
без учета потерь мощности. Далее кольцевая
сеть разрезается по точке потокораздела
на две разомкнутые сети, которые
рассчитываются с учетом потерь мощности.
Уточненный
расчет режима кольцевой сети рассмотрим
на примере расчета кольцевого участка
смешанного варианта сети, предварительный
расчет которого выполнен в 1.6.2.
Схема выделенного
кольцевого участка этой сети приведена
на рисунке 3.5
Рисунок
3.5
Схема
замещения кольцевого участка приведена
на рисунке 3.6.
Рисунок
3.6
Расчеты
зарядных мощностей ЛЭП кольцевого
участка в нормальном режиме выполнены
по формуле 3.1 и результаты сведены в
таблицу 3.9.
Таблица
3.9
|
Участок |
Число цепей |
bij, мкСм |
Qc |
|
0-1 |
1 |
94,15 |
1,14 |
|
0-2 |
1 |
94,15 |
1,14 |
|
1-2 |
1 |
129 |
1,56 |
Расчетные
нагрузки узлов определены по выражениям
3.2 — 3.7 и а результаты расчетов приведены
в таблице 3.
10.
Таблица
3.10 – Расчетные нагрузки (нормальный
режим максимальных нагрузок)
|
№ |
Рi |
Qi, |
Qci, |
Pхх |
Pпi, |
Qххпi, |
Qпi, |
Ppi, |
Qpi, |
Spi, |
|
1 |
20 |
5,288 |
1,35 |
0,028 |
0,128 |
0,180 |
2,247 |
20,16 |
6,36 |
21,14 |
|
2 |
25 |
6,61 |
1,35 |
0,04 |
0,11 |
0,27 |
2,19 |
25,15 |
7,73 |
26,31 |
Расчетная
схема сети для рассматриваемого примера
приведена на рисунке 3.
7.
Рисунок
3.7 — Расчетная схема
На
первом этапе рассчитываем кольцевой
участок без учета потерь мощности.
Найдем
поток мощности на головном участке 0-1
,
(3.40)
где
комплексно сопряженное сопротивление
участкаi-j.
Сопротивления
участков сети для рассматриваемой сети
приведены в таблице 1.21
Если
все участки кольцевой сети имеют
одинаковое сечение, то в формуле 3.40
можно вместо комплексно-сопряженных
сопротивлений использовать длины
соответствующих участков.
По
первому закону Кирхгофа
(3.41)
(3.42)
Проверка
1:
(3.43)
Проверка
2
Мощность
источника
(3.44)
Мощность
потребителей
(3.
45)
Условие
проверки
(3.46)
Условие
выполняется
Находим точку
потокораздела. В данном случае это будет
узел 2. На рисунке 3.7 точка потоказдела
помечена знаком ▼.
Разрезаем
кольцевой участок по точке потокораздела
на два разомкнутых участка (рисунок
3.8).
Рисунок
3.8
Нагрузки
узлов 2 и 2‘
определяются
из предыдущего расчета
Далее
оба участка рассчитываем с учетом потерь
мощности по методике изложенной в пп.
3.5.1.
При
этом расчет целесообразно начинать с
более простого участка (в данном примере
с участка 0-2).
Рассчитаем
режим участка 0-2 для максимальных
нагрузок
Расчетная
схема участка приведена на рисунке 3.9
Рисунок
3.
9
Принимаем
U2
= Uн
= 110 кВ
Мощность
в конце участка 0-2
(3.47)
МВА
МВА
Потери
мощности на участке 0-1
(3.48)
МВА
Мощность
в начале участка 0-2
(3.49)
МВА
Определим
напряжение в узле 1 через продольную
составляющие падения напряжения
,
(3.50)
По
заданию напряжение на шинах РЭС в режиме
максимальных нагрузок U0=1.1*Uн
= 1,1*110=121 кВ.
Уточняем
потери мощности на участке 0-2
Далее
рассчитываем с учетом потерь мощности
участок 0-1-2‘.
Расчетная
схема участка приведена на рисунке 3.10
Рисунок
3.
10
Так
как точки 2 и 2‘
(рисунок 3.8) по сути, составляют одну
точку то напряжение в точке 2‘
будет точно таким же, как в точке 2,
которое определено формулой 3.50, U2
= 118.24 кВ.
Таким
образом, расчет участка 1-2, а затем и 0-1
можно вести по известному напряжению
в конце участка и известной нагрузке,
то есть в один этап без использования
итерационных расчетов.
Мощность
в конце участка 1-2
МВА
МВА
Напряжение
в узле 1
,
(3.51)
кВ
Потери
мощности на участке 1-2
Мощность
в начале участка 1-2
МВА
Мощность
в конце участка 0-1
(3.52)
МВА
МВА
Потери
мощности на участке 0-1
МВА
На
этом расчет режима сети закончен,
поскольку определены напряжения во
всех узлах и потери мощности на всех
участках.
Проверим
правильность проведенных расчетов,
определив расчетным путем напряжение
в узле 0 (шины РЭС) и сравнив его с заданным
напряжением в режиме максимальных
нагрузок равным 121 кВ.
,
(3.53)
Погрешность
расчета составляет
,
то
есть менее одного процента, что вполне
допустимо.
Расчет
аварийных режимов кольцевого участка
заключается в поочередном отключении
головных участков 0-1 и 0-2 и расчета
соответствующих разомкнутых сетей, как
это описано в пп. 3.5.1.
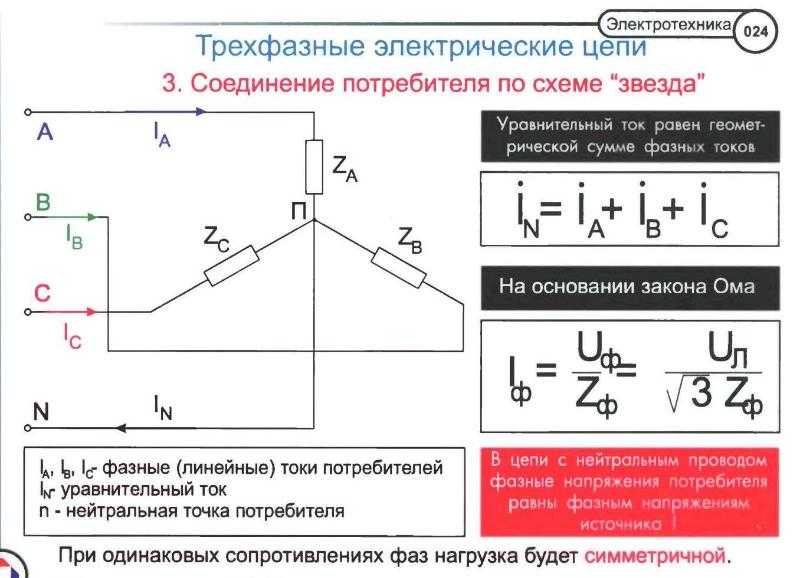
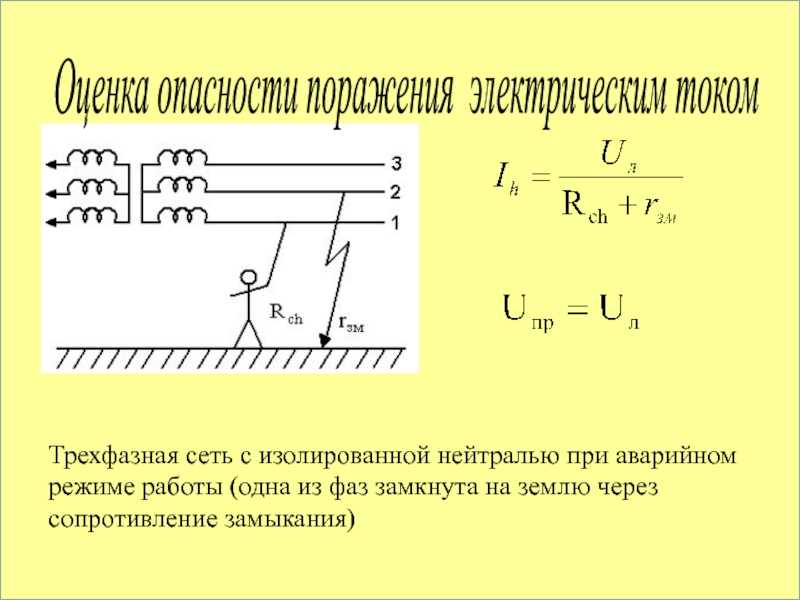
Расчет режимов электрических сетей — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1.
Лекция № 9 Расчет режимов электрических сетей
Задача расчета режимов. Основные допущения
Задача расчета режима заключается в определении параметров режима, к
которым относятся:
— значения токов в элементах сети;
— значения напряжений в узлах сети;
— значения мощностей в начале и конце элемента сети;
-значения потерь мощности и электроэнергии.
Расчет этих величин необходим для:
— выбора оборудования,
— обеспечения качества электроэнергии,
— оптимизации режимов работы сетей.
Исходными данными для расчета режима являются:
— схема электрических соединений и ее параметры – значения сопротивлений и
проводимостей ее элементов;
— мощности нагрузок или их графики мощности;
— значения напряжений в отдельных точках сети.
1
Теоретически сеть можно рассчитать с помощью методов, основанных на
законах Кирхгофа. Однако, непосредственное их применение затруднено по
двум причинам:
большое количество элементов в реальной сети;
специфика задания исходных данных.
Специфика задания исходных данных заключается в следующем –
задаются мощности нагрузок и напряжение на источнике питания. Для того,
чтобы построить картину потокораспределения, т.е. найти значения мощностей в
конце и начале каждого элемента, нужно вычислить потери мощности. Для их
вычисления необходимо знать ток в каждом элементе. Его значение можно
вычислить при известном напряжении на шинах нагрузки. А оно в начале
расчета неизвестно. Поэтому применять законы Кирхгофа непосредственно для
получения однозначного решения невозможно.
2
Основным методом расчета режимов электрических сетей является
метод последовательных приближений – итерационнный метод.
Он заключается в том, что в начале расчета задаются первым
приближением напряжений в узлах (нулевая итерация).
Обычно за нулевую итерацию принимают допущение о том, что
напряжения во всех узлах схемы равны между собой и равны номинальному
значению сети.
По принятому значению напряжения и заданной мощности потребителей
рассчитываются значения параметров режима, в том числе и значения
напряжения в узлах сети.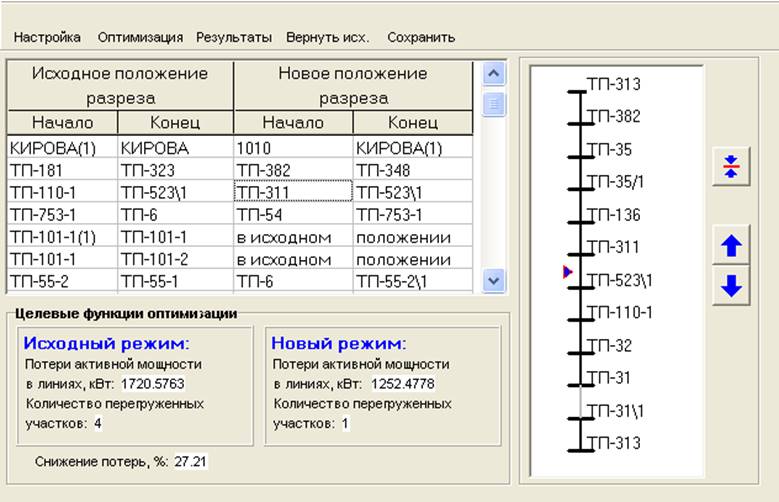
Эти значения напряжения являются вторым приближением(первой
итерацией).
Расчет повторяют до тех пор, пока результаты последующих приближений
не будут отличаться друг от друга с заданной точностью.
Чаще всего достаточно 1-2 итераций. Если же решаются задачи оптимизации
режима, связанные с потерями мощности, то требуется большое количество
итераций
3
Возможность малого количества итераций привела к появлению
нестрогих, но дающих приемлемые результаты, методов.
Такими методами являются:
метод расчета режима при заданном напряжении в конце ЛЭП;
метод расчета режима при заданном напряжении в начале ЛЭП (на источнике
питания).
4
5. Метод расчета режима при заданном напряжении в конце ЛЭП
Рассмотрим порядок расчета на примере схемы, показанной на рис. 9.1.
ИП
Уч-к1
1
Pн1+ j Qн1
Уч-к2
2
Pн2+ j Qн2
Уч-к(n-1)
n-1
Уч-кn
Pн(n-1)+ j Qн(n-1)
n
Un
Pнn + j Qнn
Рисунок 9.1 – К расчету режима при заданном напряжении
в конце ЛЭП.
Известны:
мощности нагрузок;
сопротивления и проводимости участков ЛЭП;
напряжение в конце последнего участка ( напряжение в узле n).
Расчет заключается в последовательном определении при движении от конца ЛЭП к ее
началу неизвестных мощностей и напряжений при использовании законов Ома и
Кирхгофа.
5
Последовательность расчета.
1. Определяются мощности, входящие в обмотку высшего напряжения
трансформаторов
‘
‘
Pт Pнi Pмд ;
Qт Qнi Qмд ,
где Pмд , Qмд потери активной и реактивной мощности в меди
трансформаторов.
2. Определяются приведенные нагрузки всех потребителей
Pпр Pт’ Pст ;
Qпр Qт’ Qст ,
где Pст , Qст потери активной и реактивной мощности в стали трансформаторов.
3. Определяется зарядная мощность последнего n узла
Qc n 0,5 U n2 Bn ,
где
реактивная проводимость последнего n–го участка ЛЭП, рассчитанная с
Bn
учетом
количества цепей,
Bn nц b0 l.
4.Определяется расчетная нагрузка последнего узла
Pр n Pпр n ;
Qр n Qпр n Qc n .
6
5. Определяется мощность в конце последнего n–го участка ЛЭП
Pn» Pр n ;
Qn» Qр n .
6. Определяется потери мощности на последнем n–м участке ЛЭП
( Pn» ) 2 (Qn» ) 2
S n Pn j Qn
( Rn jX n ),
U n2
где Rn , X n активное и реактивное сопротивление последнего n–го участка
ЛЭП, определенное с учетом количества цепей на участке
Rn
r0 l
;
nц
Xn
x0 l
.
nц
7.Определяется мощность в начале последнего n–го участка ЛЭП
Pn’ Pn» Pn ;
Qn’ Qn» Qn .
8. Определяются составляющие падения напряжения на последнем n–м
участке ЛЭП
Pn» Rn Qn» X n
U n
;
Un
7
Pn» X n Qn» Rn
U n
Un
(учитывается при U ном 220 кВ ).
9.Определяется напряжение в начале последнего n–го участка или напряжение узла
(n–1) при условии совмещения вектора напряжения с осью отчета аргумента
U n 1 (U n U n ) 2 U n2 .
10.Определяется зарядная мощность (n-1) узла
Qc n 1 0,5 U n2 1 ( Bn 1 Bn ).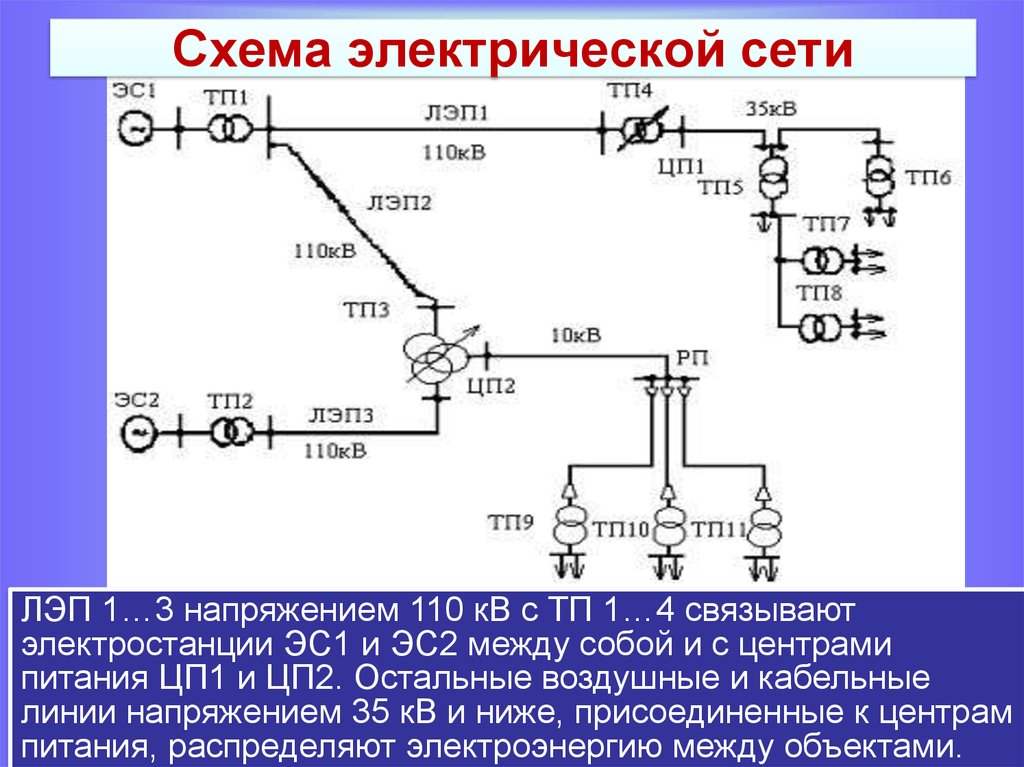
11.Определяется расчетная нагрузка (n-1) узла
Pр n 1 Pпр n 1 ;
Qр n 1 Qпр n 1 Qc n 1.
12.По I закону Кирхгофа определяется мощность в конце n–го участка
ЛЭП
Pn» 1 Pр n 1 Pn’ ;
Qn» 1 Qр n 1 Qn’ .
Далее расчет по пунктам 6 – 12 выполняется до тех пор пока не будет найдена
мощность в начале первого участка.
8
9. Расчет режима при заданном напряжении в начале ЛЭП (на источнике питания)
Этапы расчета покажем применительно к схеме, показанной на рис. 9.2.
ИП
Уч-к1
1
Уч-к2
2
Уч-к(n-1)
n-1
Уч-кn
n
Uип
Pн1+ j Qн1
Pн2+ j Qн2
Pн(n-1)+ j Qн(n-1)
Pнn + j Qнn
Рисунок 9.2 – К расчету режима при заданном напряжении
на источнике питания.
Известны:
мощности нагрузок;
сопротивления и проводимости участков ЛЭП;
напряжение на источнике питания.
В этом случае невозможно последовательно от конца ЛЭП к началу определить
неизвестные мощности и напряжения по I закону Кирхгофа, так как напряжение
в конце участка неизвестно.
В этом случае используется метод
последовательных приближений. Расчеты выполняются в два этапа.
9
10
11
12
English
Русский
Правила
Расчеты установившихся режимов сложной сети путем приведения ее к эквивалентным открытым
Открытый доступ
| Проблема |
Веб-конференция E3S. Том 58, 2018 Руденко Международная конференция «Методические проблемы исследования надежности больших энергетических систем» (РСЭС 2018) |
|
|---|---|---|
| Номер статьи | 02022 | |
| Количество страниц) | 6 | |
| Секция | Модели и методы оценки надежности интеллектуальных энергетических систем | |
| ДОИ |
https://doi.org/10.1051/e3sconf/20185802022 |
|
| Опубликовано онлайн |
10 октября 2018 г.
|
|
E3S Web of Conferences 58 , 02022 (2018)
Dauren Akhmetbayev 1 , Assemgul Zhantlessova 1 * and Arman Akhmetbayev 2
1
Кафедра электроснабжения, Казахский агротехнический университет им. С.Сейфуллина, Казахстан
2
Дирекция информационных систем АО «Казтелеком», Казахстан
* Автор, ответственный за переписку: [email protected]
Abstract
В статье рассмотрено развитие идеи диакоптики применительно к расчету установившихся режимов сложных электрических сетей энергосистемы. Известная цель диакоптики — получение уравнений состояния выделенной части системы, исследование которых значительно проще исследования исходной системы и может быть достигнуто за счет уточнения ее уравнений стационарного состояния. Разработана методика разбиения сложной замкнутой системы на множество несложных подсистем на основе обратной формы узловых уравнений.
Предложены аналитические выражения для цепей пересечения, полученные на основе одинакового равенства напряжений в узлах разделения системы на подсистемы. На примере расчета сети 110 кВ показана методика определения матриц обобщенных параметров выделенных подсистем, размеры которых зависят от количества их разомкнутых звеньев. Аналитическое определение условия равенства напряжений узлов пересечения подсистем позволило провести анализ сложной замкнутой сети путем приведения ее к эквивалентной разомкнутой.
© The Authors, опубликовано EDP Sciences, 2018 г. разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Показатели текущего использования показывают совокупное количество просмотров статей (просмотры полнотекстовых статей, включая просмотры HTML, загрузки PDF и ePub, согласно имеющимся данным) и просмотров рефератов на платформе Vision4Press.
Данные соответствуют использованию на платформе после 2015 года.
Текущие показатели использования доступны через 48-96 часов после онлайн-публикации и обновляются ежедневно в рабочие дни.
Расчет установившихся несинусоидальных режимов и потерь электроэнергии в сложных электрических сетях
-
title={Расчет установившихся несинусоидальных режимов и потерь электроэнергии в сложных электрических сетях},
автор={Н. Н. Харлов и В.С. Боровиков и Василий Я. Ушаков, Е.В. Тарасов, Л.Л. Булыга},
Journal={2016 Международная конференция IEEE по силовой электронике и управлению движением (PEMC)},
год = {2016},
страницы={336-341}
}- Харлов Н., Боровиков В., Булыга Л.Л.
- Опубликовано 1 сентября 2016 г. предложен режим сложной электрической сети с учетом распределения параметров воздушных линий электропередачи, геометрии подвески и марки проводов, наличия грозозащитных тросов и способа их заземления по трассе линии. На основе расчета установившегося режима сложной сети учитываются основные потери, вызванные токами прямой последовательности основной частоты…
Просмотр на IEEE
doi.
org Расчет случайных потерь электроэнергии на несинусоидальных режимах с учетом фактического нагрева проводящих частей
- Долгих Н.Н., Коваленко Д., Файфер Л.
Машиностроение
2018 Международная конференция по промышленному инжинирингу, применению и производству (ICIEAM)
- 2018
В работе представлено использование вейвлет-пакетного преобразования для анализа несинусоидального режима систем электроснабжения с учетом фактического нагрева проводящих частей. . Высшие гармоники вызывают…
Сравнение производительности фильтра с одинарной настройкой и фильтра с-типа в распределительной сети электроэнергии гармоническое содержание.
Влияние индекса модуляции на гармоники инвертора SP-PWM, питающего универсальный двигатель
- А. А. Соланги, М. Гул, Р. Шайх, Ф. Умер, Н. К. Патан, З. Мемон
-
Engineering
- 2018
Влияние индекса модуляции (MI) используется для анализа содержания THD, и его изменение изменяет содержание гармоник, а эффекты анализируются с помощью моделирования и экспериментальной установки для проверки производительности системы.
ПОКАЗАНЫ 1-10 ИЗ 18 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные статьиНедавность
Расчет потерь на основе измерений и оптимизация в сетях низкого напряжения
Потери энергии в электрических сетях обычно оцениваются путем уравновешивания подаваемой и отдаваемой энергии анализируемой области сети. Как правило, невозможно получить информацию для снижения убытков…
Аспекты, касающиеся возможностей мониторинга и стационарного анализа сетей перераспределения электроэнергии
- Б. Неагу, Г. Джорджеску
-
Инженерия, физика
2014 Международная конференция и выставка по электротехнике и энергетике (EPE)
- 2014
С технико-экономической точки зрения рациональная и эффективная работа систем перераспределения и распределения электроэнергии обусловлена их способностью увеличивать…
Статистический метод минимизации потерь электроэнергии в местной распределительной сети
- J. W. Fourie, J. E. Calmeyer
-
Engineering, Physics
2004 IEEE Africon. 7-я Африканская конференция в Африке (№ по каталогу IEEE 04Ch47590)
- 2004
Основной областью исследований в области управления энергопотреблением является снижение потерь электроэнергии в распределительных сетях. Эти потери являются техническими и нетехническими потерями…
Анализ уровней гармонических искажений в распределительной сети
- G. Nicholson, V. Gosbell, A. Parsotam
-
Environmental Science
2007 Австралийские университеты. уровни гармонических искажений в распределительных сетях медленно, но неуклонно растут из-за распространения нелинейных нагрузок. При рассмотрении жалоб потребителей…
Оценка потерь электроэнергии в распределительных сетях для целей планирования
- J. Dickert, M. Hable, P. Schegner
-
Физика, инженерия
2009 IEEE Bucharest PowerTech
- 2009
Доступный метод оценки потерь энергии (т.
е. , потери мощности при пиковой нагрузке) будут выведены и реализованы, а уже разработанные аппроксимационные формулы будут пересмотрены для использования в существующих сетях с сегодняшними характеристиками нагрузки. Оценка состояния энергосистем на основе минимальных потерь информации
На основе теории информации изучены математические основы метода оценки состояния (ОС) энергосистем. Более общий метод SE, основанный на принципе минимальной потери информации (MIL), представляет собой…
Основы электротехники
- Л. Бобров
-
Инженерия
- 1995
Основные элементы и схемы. 1.1 Источники напряжения, источники тока и резисторы 1.2 Закон Кирхгофа для тока (KCL) 1.3 Закон Кирхгофа для напряжения (KVL) 1.4 Независимый и зависимый…
Менеджмент качества электроэнергии как перерабатываемого материала
- Р. Сасделли, Г. Гоббо, Г. Иукулано
-
Инженерное дело
IMTC/99. Материалы 16-й конференции IEEE по приборостроению и измерительным технологиям (Cat.
- Долгих Н.Н., Коваленко Д., Файфер Л.
org 
W. Fourie, J. E. Calmeyer 
е. , потери мощности при пиковой нагрузке) будут выведены и реализованы, а уже разработанные аппроксимационные формулы будут пересмотрены для использования в существующих сетях с сегодняшними характеристиками нагрузки. 
Добавить комментарий