Содержание
Построение графика функции в полярных координатах · Калькулятор Онлайн
Графики функций/ В полярных координатах
Введите график функции
Важно
phi должно лежать в правильном промежутке, иначе график не сможет построиться
Построим график функции в полярных координатах r=r(φ),
где 0 <= φ <= 2π,
но вы можете задать свои границы φ.
Задайте также полярную функцию r(φ).
Примеры кривых
| Название кривой | Уравнение | |
|---|---|---|
| Окружность |
1 p в [0, 2*pi] |
|
| Спираль Архимеда |
2*p p в [0, 8*pi] |
|
| Кардиоида |
1 - sin(p) p в [0, 2*pi] |
|
| Улитка Паскаля |
2 - 4*sin(p) p в [0, 2*pi] |
|
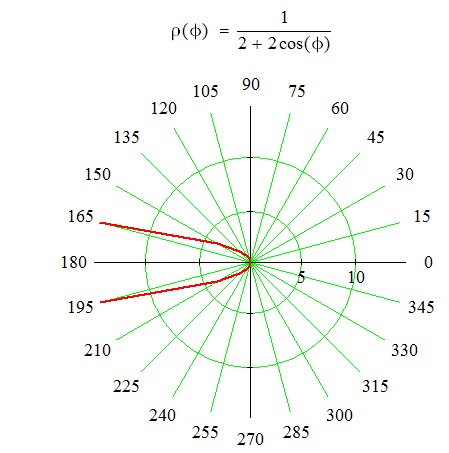
| Парабола |
1/(1 - cos(p)) p в [0, 2*pi] |
|
| Полярная роза |
sin(6*p) p в [0, 2*pi] |
|
sin(3*p/4) p в [0, 8*pi] |
||
| Бабочка |
exp(sin(p)) - 2*cos(4*p) + sin((2*p - pi)/24)^5 p в [-8*pi, 8*pi] |
|
| Сердце |
2 - 2*sin(p) + sin(p)*sqrt(|cos(p)|)/(sin(p) + 1. Интегральные функции:
В выражениях можно применять следующие операции:
Другие функции:
Постоянные:
|
Многомерное исчисление
. Какие формы описываются с помощью $\rho = \cos{(\phi)}$ и $\rho = \cos{(2\theta)}$?
Задавать вопрос
спросил
Изменено
6 лет, 3 месяца назад
Просмотрено
20 тысяч раз
$\begingroup$
Я начал курс Multivariable и изучаю сферические координаты. Моя проблема сейчас состоит в том, чтобы научиться рисовать такие фигуры.
Вот задача:
Какие фигуры описываются, когда...?
Решение:
a) $\rho = 1$ : сфера радиуса 1.
b) $\phi = \frac{\pi}{3}$ : конус с углом $\frac{\pi}{ 3}$.
c) $\theta = \frac{\pi}{4}$ : Полукруглое поперечное сечение с диаметром по оси z
г) $\rho = \cos{(\phi)}$ : ?
e) $\rho = \cos{(2\theta)}$ : .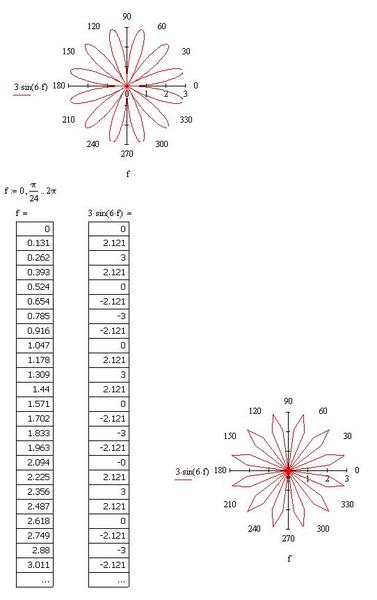
Верны ли они? Как словесно описать два последних -d) и e).
- многомерное исчисление
$\endgroup$
5
$\begingroup$
Если $\phi$ — конус с углом $\pi/3$, то:
г) $\rho=\cos\phi$:
92=г,
$$
которая представляет собой сферу радиуса $1/2$ с центром в точке $(0,0,1/2)$:
e) $\rho=\cos2\theta$:
Мы могли бы найти здесь декартово уравнение, но это не поможет, так как это не классическая поверхность:
а), б) и в) верны. Чтобы убедиться в этом, найдите декартовы уравнения.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Исчисление
- Почему $r = \cos\theta$ создает круг?
спросил
Изменено
6 лет назад
Просмотрено
38 тысяч раз
$\begingroup$
Я пытаюсь выполнить двойной интеграл по следующей области в полярных координатах:
Я знаю, что пределы интегрирования таковы:
$$\theta = -\frac{\pi}{2} \quad \to \quad \theta = \frac{\pi}{2} \\ r = 0 \quad \to \quad r = \cos \theta$$
Однако я не понимаю, как $r = 0 \ quad \to \quad r = \cos\theta$ работает. Косинус — это функция (а не просто отношение), означающая, что она имеет только одно значение $r$ для каждого значения $\theta$. Однако кажется, что граф $r = \cos\theta$ имеет два значения $r$ для каждого значения $\theta$.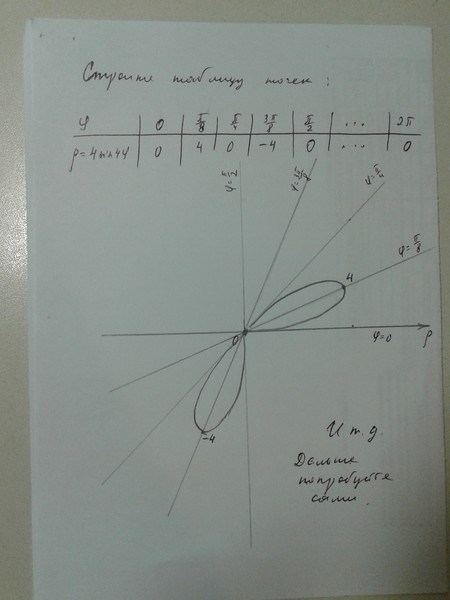
$\endgroup$
$\begingroup$
Вот более геометрический способ взглянуть на это.
Поскольку $0$ является возможным значением $\cos\theta$, геометрическое место содержит начало координат $O$. Поскольку $\cos 0=1$, геометрическое место включает $A=(1,0)$.
Пусть теперь $B$ будет любой другой точкой на геометрическом месте $r=\cos\theta$. Тогда $OA$ измеряет 1, $\angle AOB$ измеряет $\theta$, а $OB$ измеряет $\cos\theta$. Решаем треугольник $OAB$ и обнаруживаем, что угол при $B$ прямой. Тогда геометрическое место точек $B$ таких, что $\угол ABO$ является прямым углом для пары неподвижных точек $A$ и $O$ плюс неподвижные точки, является окружностью. 92=\frac14$$
и у вас есть красивая окружность с центром в $\;(1/2\,\,0)\;$ и радиусом $\;1/2\;$
$\endgroup$
$\begingroup$
В декартовых координатах $(\cos\alpha,\sin\alpha)$ — это окружность.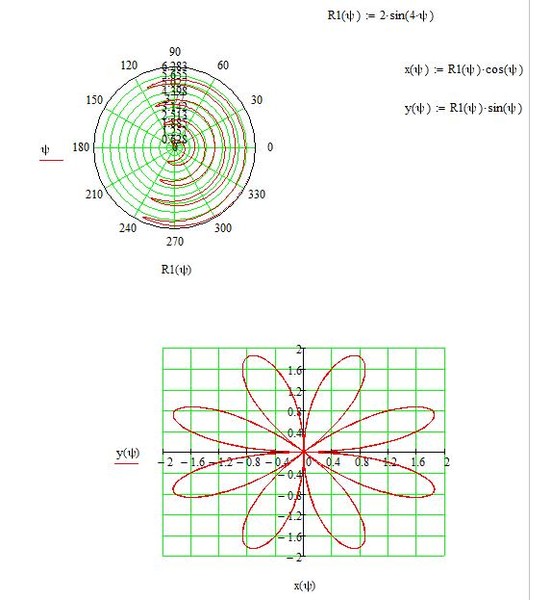
$\endgroup$
$\begingroup$
Чтобы понять, почему график отображает функцию, игнорируя на данный момент начало координат, обратите внимание, что «тест вертикальной линии», о котором вы, возможно, подумали, не подходит для полярных функций. Каждое значение $\theta$ указывает линию, проходящую через начало координат, и именно эта линия должна проходить только через одну точку на графике. Однако этот тест по-прежнему неприемлем, потому что существует несколько значений $\theta$, которые определяют одну и ту же линию, проходящую через начало координат (в частности, $\theta+\pi n$ для каждого целого числа $n$), поэтому для графа возможно полярной функции, чтобы многие значения проходили через одну и ту же прямую через начало координат.
В данном конкретном случае каждая невертикальная линия, проходящая через начало координат, проходит через две точки графика: одну в начале координат, а другую в другом месте.
.jpg) 3
3
 2
2
Добавить комментарий