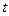Нагревание и охлаждение идеального однородного твердого тела. Постоянная времени нагреваФизический смысл постоянной нагрева электродвигателяРассмотрение процессов охлаждения и нагрева электрических машин показало, что в значительной степени характер протекания процессов зависит от постоянной нагрева Θ. Поэтому для лучшего понимания этих процессов необходимо более подробно остановится на постоянной нагрева. Постоянная нагрева имеет вид:
То есть отчетливо видно, что данная величина имеет размерность времени. При одной и той же мощности электрической машины постоянная нагрева будет зависеть от габаритов электродвигателя. Для закрытых двигателей, имеющих большой габарит, постоянная нагрева будет больше, чем для электрических машин защищенного или открытого исполнения. Также не последнюю роль играют и условия охлаждения электродвигателя. Например, для электрических машин с самовентиляцией, где отвод тепла довольно интенсивен, Θ имеет небольшое значение, а для электрической машины закрытого типа, где отвод выделяемого тепла затруднен, Θ будет больше. При уменьшении скорости вращения двигателя ухудшается и вентиляция, что приводит к более интенсивному нагреву электродвигателя. Например, для электрических машин постоянного тока с самовентиляцией при неподвижном якоре постоянная нагрева возрастает в два – два с половиной раза. Постоянная нагрева асинхронных электродвигателей общепромышленного исполнения при неподвижном роторе достигает порядка 4 – 4,5 кратного при вращении значения Θ. Θ будет постоянна только в электрических машинах с принудительной вентиляцией, где интенсивность охлаждения не будет зависеть от скорости вращения. Определение Θ может быть определено из уравнений нагрева (10) и охлаждения (13). Полагая в каждом из них продолжительность процесса равную постоянной нагрева, получим то или иное значение температуры перегрева машины. В связи этим, постоянной времени нагрева называют время, в течении которого при постоянном сообщении тепла электрическая машина достигнет 0,632τнач, или машина остывая достигнет 0,368τу. Физический смысл постоянной нагрева таков – это время, в течении которого превышение температуры электродвигателя достигнет установившегося значения, при этом отдача тепла в окружающую среду самим электродвигателем отсутствует. При этих условиях А = 0 и основное уравнение нагрева примет вид:
В случае протекания процесса от холодного состояния при t = 0 и τ = 0 интеграл описанного выше выражения принимает вид:
Таким образом, при отсутствии теплообмена тела с окружающей средой перегрев происходит по закону прямой линии. Подставляя в полученное выражение значение установившегося превышения температуры τу = Q/A получим:
Как правило, в качестве постоянной нагрева принимают наиболее ответственную часть машины, отображающую общий тепловой режим работы. В качестве подобных элементов обычно берут якорь у машин постоянного тока, а у асинхронных и синхронных машин – статор. Получение значения Θ расчетным путем возможно, но недостаточно точно. Поэтому, как правило, постоянную нагрева определяют экспериментальным путем. Для этого по данным опыта строят кривую превышения температуры функцией от времени τ =f(t) и на этом графике наносят асимптоту, соответствующую установившемуся значению превышения температуры τу = Q/A. Ввиду того, что получение установившейся температуры при больших значениях Θ требует большой длительности эксперимента, обычно асимптотические значения τу находят с помощью вспомогательного построения. Для этого в координатных осях τ и t строят экспериментально снятую кривую τ =f(t):
Но оси t откладывают равные отрезки Δt и через них проводят вертикали до пересечения с кривой. Через полученные точки пересечения проводят горизонтальные прямые, продолжая их влево за ось ординат. На проведенных влево горизонтальных прямых от оси ординат откладывают отрезки, пропорциональные Δτ – приращению температуры за соответствующий промежуток времени Δt. Точка пересечения с прямой, проведенной через концы отрезков kΔτi,и оси ординат дает величину τу. Это видно из следующих соотношений. Нагрев электродвигателя в некоторой точке i будет равен:
А в соседней точке i + 1:
Повышение температуры при этом составит:
Из уравнения (4):
Заменив в предыдущем выражении
В этом уравнении Для определения постоянной нагрева проводят касательную к любой точке кривой нагрева и продолжают ее до пересечения с прямой τу = const. Отрезок на асимптоте, отсекаемый касательной и вертикалью, проведенный через точку касания, дает величину постоянной нагрева. Действительно, уравнение касательной и кривой в точке t1 и τ1 будет равно:
Величина углового коэффициента касательной равна:
Абсцисса t2 точки пересечения касательной с асимптотой τ = τу может быть определена из выражения:
Пользуясь основным уравнением нагрева, легко показать, что дробь, состоящая из правой части, равна единице, так как:
Таким образом, t2 – t1 = Θ. Графическое определение значения постоянной нагрева для ряда точек кривой нарастания температуры показано ниже:
Особенно легко получается определение в случае если касательная проводится в начале координат. В этом случае постоянная получается в виде отрезка, отсекаемого касательной на асимптоте. На этой же фигуре указано, что при увеличении нагрузки двигателя возрастает установившаяся температура перегрева, но Θ при этом остается неизменной. В однотипных машинах Θ возрастает с увеличением габаритов машины. Это легко доказать воспользовавшись общим выражением постоянной нагрева Θ = С/А. Теплоемкость электрической машины С возрастает пропорционально объему или кубу линейных размеров, а охлаждающая поверхность увеличивается пропорционально квадрату линейных размеров. Таким образом, в первом приближении можно считать, что постоянная нагрева растет пропорционально линейным размерам машины:
Значения Θ в каталогах производителей электрических машин не приводится, поэтому систематизированные данные привести затруднительно. Но на основании многих литературных источников приблизительно можно считать, что постоянная нагрева для:
Зависимость Θ якорей машин постоянного тока типа МП от диаметра приведена ниже:
Следует помнить, что рассмотренные выше экспоненциальные зависимости температуры нагрева имеют место лишь при рассмотрении электродвигателя как твердого однородного тела. В реальных условиях процессы нагревания и охлаждения электрических машин будут проходить сложнее. При работе электродвигателя потери в меди и стали вызывают нагревание. Однако благодаря сравнительно небольшой массе и высокой теплопроводимости обмотка будет нагреваться значительно быстрее активной стали электродвигателя. Это вызвано тем, что масса стали значительно больше, а потери в ней намного меньше чем в меди. Сталь, в следствии своей большой охлаждающей поверхности, всегда остается менее нагретой, чем медь, и благодаря этому существует перепад температур между медью и сталью, вызывающий длительный обмен теплом. Дополнительный подогрев со стороны обмотки вызывает более быстрый нагрев стали, а повышение температуры меди в следствии данного теплообмена замедляется. Именно поэтому кривая нагрева обмотки вначале идет круче экспоненты, и только при установившемся процессе совпадает с экспонентой и становится практически параллельной оси времени. В качестве примера ниже приведена кривая полученная экспериментальным путем:
Здесь кривая 1 – нагрев обмотки статора асинхронного электродвигателя МА-200 мощностью 15 кВт и n = 1500 об/мин. На этом же графике изображена экспоненциальная кривая 2 с Θ = 20 мин. Наиболее значительны расхождения экспериментальной и расчетной характеристики нагрева (рассчитанной по приведенным выше формулам), как правило, возникают в начале нагрева. elenergi.ru Постоянные времени нагрева и охлажденияПостоянную времени нагрева – в уравнении (7-5) можно определить, подставив времяв (7-6а)
получим:
. Постоянная времени нагрева – это время, в течении которого превышение температуры двигателя над окружающей средой, при неизменных условиях работы, достигнет значения .[чилк353] Двигатель в процессе охлаждения, стремится к температуре окружающей среды – этот период может быть очень длительным. Для практических целей считают двигатель остывшим полностью, если его температура отличается от температуры окружающей среды не более чем на 3. Подставим в уравнение охлаждения:
и получим:
Постоянная времени охлаждения – это время, в течении которого превышение температуры двигателя над окружающей средой, при неизменных условиях работы, достигнет значения . Постоянные времени нагрева и охлаждения двигателя зависят от его массы, а следовательно и от мощности. Чек 302 28.02.13 321сп прогуи ТЕМА ЛЕКЦИИ 8 Классификация режимов работы судового электрооборудования в зависимости от продолжительности рабочего цикла План лекции
Судовое электрооборудование будет работать надежно, если оно не только правильно сконструировано, но и правильно используется.СЭО используется правильно, если оно соответствует условиям работы судового механизма, устройства и т.п. Поясним сказанное на примере условий работы электродвигателей. Например, электродвигатели насосов и вентиляторов работают с постоянной нагрузкой, при неизменном токе. В то же время электродвигатели грузоподъемных механизмов работают в более тяжелых условиях – с частыми пусками, сопровождающимися бросками тока. Ясно, что использовать в грузоподъемных механизмах электродвигатели, предназначенные для насосов или вентиляторов нельзя – они быстро сгорят. Если, наоборот, использовать для насосов или вентиляторов электродвигатели, предназначенные для грузоподъемных механизмов, можно, но нецелесообразно – они окажутся недоиспользованными по мощности, т.к. вместо работы в тяжелых условиях (с бросками токов) они станут работать в легких (с постоянной нагрузкой). Таким образом, каждому виду СЭО соответствует «свой», определенный режим работы. Тот или иной режим работы электрооборудования полностью зависит от технологических условий работы. То есть, механизм «навязывает» электрооборудованию (например, электродвигателю) свои условия работы – как работает механизм, так должен работать и электродвигатель. Приведем основные сведения, связанные с понятием «режим работы электрооборудования», применительно к электродвигателям. Это объясняется тем, что основную часть производимой на судне электроэнергии (до 85…90%) потребляют именно электродвигатели. studfiles.net 6.1.1 Способы определения постоянной времени нагревания и установившегося превышения температурыПервый способ. Строится экспериментальная кривая нагревания (рис. 15). К полученной кривой проводится касательная в начальной точке A. Отрезок АВ, отсекаемый касательной к кривой нагревания на асимптоте уст, дает постоянную времени в масштабе оси абсцисс. Данный способ весьма приблизителен и требует знания установившегося перегрева.
Второй способ. На экспериментальной кривой (рис. 16) выделяется некоторый участок ab в верхней части. В точках a и b проводятся касательные к кривой нагревания и находятся tg1 и tg2 либо путем измерения углов 1 и 2, либо из соотношения катетов прямоугольных треугольников ( apq, bp'q'). В любом приемлемом масштабе mtg на прямых параллельных оси абсцисс и проходящих через точки a и b откладываются найденные значения тангенсов в виде отрезков fc и mn: (33) Через полученные точки c и n проводится прямая до пересечения с осями абсцисс и ординат. Эта прямая пересечет ось ординат в точке уст (отрезок OD). Постоянная времени нагревания определяется как отношение: (34) где OD отрезок на оси ординат, мм; OF отрезок на оси абсцисс, мм; m масштаб температуры, °C/мм; mtg масштаб тангенсов, 1/мм. Третий способ. На кривой нагревания берутся три точки, отстоящие друг от друга на равные промежутки времени t (рис. 17). Постоянная времени в этом случае: (35) Установившуюся температуру можно найти по методике, описанной во втором способе расчета или графическим способом, приведенным в ГОСТ 3484.2-88 [6]. По ГОСТ 3484.2-88 на кривой нагревания берутся четыре точки, отстоящие друг от друга на равные промежутки времени (рис. 18). Измеряются приращения превышения температур 1, 2, 3. Эти приращения в любом масштабе откладываются по оси (см. рис. 18). Соответствующие точки 1, 2 и 3 должны лежать на одной прямой, которая пересечет ось ординат в точке уст.
6.1.2 Способ определения постоянной времени охлажденияОхлаждение двигателя в общем случае продолжается до уст = 0, т.е. описывается уравнением (32). Постоянную времени охлаждения достаточно просто найти путем логарифмирования (32) в любой точке кривой. Примем: (36) где τ0 начальное превышение температуры для опыта охлаждения, равное конечному значению в опыте нагревания двигателя. После логарифмирования и простых преобразований: (37) Для определения Tох нужно найти постоянную времени охлаждения по выражению (34) в трех четырех точках экспериментальной кривой и взять среднее значение. Начальное превышение температуры 0 известно из опыта нагревания. 6.2. Методические рекомендации к проведению исследований1) Изучить электрическую схему для исследования процесса нагревания и охлаждения электродвигателя (рис. 19). Лабораторная установка представляет собой асинхронный двигатель М1, соединенный механически с машиной постоянного тока M2, которая обеспечивает необходимый тормозной момент; кроме того, имеется механическая связь с датчиком частоты вращения BV. Асинхронный двигатель M1 получает питание от «Модуля питания», нагрузочная машина постоянного тока M2 подключена к модулю «Тиристорный преобразователь». Величина тормозного момента регулируется с помощью реостата RP1 Uупр модуля «Тиристорный преобразователь». Для контроля температуры асинхронного двигателя использован температурный контроллер DTB4848, установленный сверху асинхронного двигателя M1, при этом температурный датчик контроллера уложен в один из пазов статора машины. Считывание информации о значении температуры в градусах Цельсия производится непосредственно с цифрового индикатора контроллера.
Рис. 19. Электрическая схема теплового испытания электродвигателя Асинхронный двигатель M1 получает питание от «Модуля питания», нагрузочная машина постоянного тока M2 подключена к модулю «Тиристорный преобразователь». Величина тормозного момента регулируется с помощью реостата RP1 Uупр модуля «Тиристорный преобразователь». Для контроля температуры асинхронного двигателя использован температурный контроллер DTB4848, установленный сверху асинхронного двигателя M1, при этом температурный датчик контроллера уложен в один из пазов статора машины. Считывание информации о значении температуры в градусах Цельсия производится непосредственно с цифрового индикатора контроллера. 2) Собрать электрическую схему для исследования процесса нагревания и охлаждения асинхронного двигателя (рис. 19) на лабораторном стенде. 3) Привести переключатели и регулировочные элементы схемы в исходные положения: а) автоматические выключатели «Модуля питания стенда» и «Модуля питания» отключить; б) на модуле «Тиристорный преобразователь» кнопку «Сеть» отключить, переключатель SA1 перевести в положение «Iя», SA2 – «Момент», SA3 – «Руч», SA4 – «НМ», SA5 – «Вперед», SA6 «Разрешение» – отключить (перевести тумблер вниз), движок потенциометра RP1 Uупр установить в крайнее левое положение «0» (до упора против часовой стрелки). 4) Перед включением схемы необходимо, чтобы она была проверена преподавателем. 5) Последовательность действий при выполнении эксперимента по исследованию нагревания АД в длительном режиме: а) включить автоматический выключатель QF1 «Модуля питания стенда» и выполнить измерение сопротивления обмотки АД Rнач с помощью мультиметра, результат записать в табл. 11. По окончании измерения сопротивления отсоединить щупы мультиметра от АД; б) включить автоматический выключатель QF2 «Модуля питания», включить кнопку «Сеть» модуля «Тиристорный преобразователь», перевести тумблер SA6 «Разрешение» во включенное положение; в) движком потенциометра RP1 модуля «Тиристорный преобразователь» установить заданное преподавателем значение тока якоря машины постоянного тока в пределах от 0,5 до 1,0Iн тока статора АД (величина тока якоря контролируется по показаниям цифрового индикатора модуля «Тиристорный преобразователь»). После установки заданной нагрузки АД необходимо зафиксировать в табл. 11 значение частоты вращения машины nдлит. При выполнении эксперимента следует поддерживать нагрузку двигателя неизменной при помощи тиристорного преобразователя; г) снять кривую нагревания τ = f(t) в длительном режиме работы при постоянном токе (мощности) двигателя в течении времени tнагр = 30 мин.Экспериментальные точки кривой нагревания снимать через равные промежутки времени t = 2 мин, результаты измерений записать в табл. 11. д) по завершении процесса нагревания снять нагрузку с асинхронного двигателя, для этого установить RP1 в крайнее левое положение, перевести тумблер SA6 «Разрешение» в выключенное положение; отключить АД от питающей сети (выключить QF2 «Модуля питания»). С помощью мультиметра измерить сопротивление обмотки АД в «горячем состоянии» Rгор, результат записать в табл. 11, отсоединить щупы мультиметра от АД по завершению измерения; е) снять кривую охлаждения АД τ = f(t) в длительном режиме работы в условиях принудительной вентиляции в течении времени t = 30 мин, для чего модуль «Тиристорный преобразователь» перевести в режим регулирования скорости (переключатель SA2 перевести в положение «Скорость»), включить SA6 и установить потенциометром RP1 модуля «Тиристорный преобразователь» частоту вращения АД nдлит равную нагруженному двигателю в предыдущем опыте (при нагревании АД). Экспериментальные точки кривой охлаждения снимать через равные промежутки времени t = 2 мин в течении времени tохл = 30 мин, результаты измерений записать в табл. 11. По завершении процесса охлаждения установить потенциометр RP1 модуля «Тиристорный преобразователь» в крайнее левое положение «0», перевести тумблер SA6 «Разрешение» в выключенное положение; Т а б л и ц а 11 Экспериментальные данные тепловых процессов АД в длительном режиме
ж) по завершении процесса охлаждения с помощью мультиметра измерить сопротивление обмотки АД Rохл, результат записать в табл. 11; з) перевести все переключатели на лабораторном стенде в исходное положение (см. п. 3). 6) Последовательность действий при выполнении эксперимента по исследованию нагревания АД в повторно-кратковременном режиме: а) включить автоматический выключатель QF1 «Модуля питания стенда» и измерить сопротивление обмотки АД Rнач с помощью мультиметра, результат записать в табл. 12. По окончании измерения сопротивления отсоединить щупы мультиметра от АД; б) включить автоматический выключатель QF2 «Модуля питания», включить кнопку «Сеть» модуля «Тиристорный преобразователь», перевести тумблер SA6 «Разрешение» во включенное положение; в) снять кривую нагревания τ = f(t) при повторно-кратковременном режиме работы (величина нагрузки, длительность рабочей ступени tвкл и паузы tоткл задаются преподавателем и записываются в табл. 12). К моменту первого включения АД температура должна быть равна температуре окружающей среды (τ0 = 0). Замеры сопротивления обмотки АД производятся в начале и конце каждой паузы нагрузки. Т а б л и ц а 12 Исходные данные для исследования повторно-кратковременного режима
– задать величину нагрузки исследуемого АД потенциометром RP1 модуля «Тиристорный преобразователь» и установить ток якоря нагрузочной машины постоянного тока Iнм (величина тока якоря контролируется по показаниям цифрового индикатора блока «Индикация» модуля «Тиристорный преобразователь») – в режиме отключения нагрузки АД работает на холостом ходу, для чего следует установить крайнее левое положение движка потенциометра RP1 модуля «Тиристорный преобразователь». В табл. 13 следует записывать значения превышения температуры τ по показаниям цифрового индикатора температурного контроллера. Измерения следует провести для четырех циклов работы АД. д) перевести все переключатели на лабораторном стенде в исходное положение (см. п. 3). Т а б л и ц а 13 Экспериментальные данные тепловых процессов АД в повторно-кратковременном режиме
studfiles.net Уравнение теплового баланса ЭП.
При работе ЭД в различных условиях и при различных нагрузках на его валу изменяются условия протекания тепловых процессов ЭД. Как известно работа ЭД сопровождается потерями мощности а во вторых рассеивается в окружающую среду:
В начале основная часть выделяемого тепла идет на нагревание самого двигателя и значительно меньшая часть отдается в окружающую среду. В процессе нагревания ЭД это соотношение изменяется в сторону 1. Эл.маш. является однородным телом с одинаковой по всему телу теплоёмкостью 2. Теплоотдача в окружающую среду пропорциональна разности температур двигателя и окружающей среды, т.е. :
Чаще всего при анализе тепловых переходных процессов в качестве
С учетом этих допущений, уравнение 3 запишется в виде:
где
теплоёмкость – численно равна количеству тепла, необходимое для нагрева двигателя на 1 градус. теплоотдача- количеству тепла, выделявшему в ОС при изменении температуры на один градус за время равное 1 секунде.
Если
Уравнение (104) описывает тепловые переходные процессы в ЭД и в частном случае для установившегося режима примет вид.
Если в уравнении (104) отношение
(105)- представляет из себя дифференциальное уравнение 1-го порядка и носит название дифференциальное уравнение теплового баланса. При нагреве от некоторого начального значения
Графически это уравнение может быть представлено в виде экспоненциальной функции следующего вида:
Рис.79
В частном случае если включение двигателя происходит в момент когда его температура равна температуре окружающей среды, график будет иметь следующий вид:
Рис.80 Если двигатель в процессе работы нагреть до
Постоянная времени нагрева. Физический смысл Если мы в уравнении (103) условно примем
Уравнение (107) решим относительно времени. за которое при этих условиях двигатель нагреется от
Учитывая, что Таким образом доказали, что физический смысл постоянной времени нагрева соответствует записанному определению нагреву. Для определения постоянной времени нагрева можно использовать решение уравнения теплового баланса в виде:
Примем в уравнении (108)
Поэтому для определения постоянной времени нагрева необходимо экспериментально, построить график
Рис.81 Однако на практике значительно чаще приходиться иметь дело с другими постановками задачи для того чтобы, кривую нагрева, необходимо знать постоянную времени нагрева. Как уже было сказано теплоотдача двигателя.
Рис.82
Необходимо отметить также, что длительность переходного режима при изменении температуры двигателя
Рис.83 infopedia.su Нагревание и охлаждение двигателя — КиберПедия
При работе электродвигателя в нем имеют место потери энергии в стали, меди и потери на трение, которые вызывают его нагревание. Процесс нагревания отдельных частей электродвигателя происходит неодинаково, так как электродвигатель представляет собой неоднородное тело и условия нагревания различных частей различны. Учет всех явлений тепловых процессов представляет весьма большие трудности. Поэтому для упрощения тепловых расчетов условно принимают, что электродвигатель представляет собой однородное в тепловом отношении тело, теплопроводность которого равна бесконечности. Кроме того, считают, что теплоотдача во внешнюю среду пропорциональна первой степени разности температур. В соответствии с принятыми допущениями уравнение теплового баланса электродвигателя при неизменной нагрузке будет иметь следующий вид: (l) где Q - количество тепла, сообщаемое электродвигателю в единицу времени, кал/сек; С - теплоёмкость тела, т.е. количество тепла, необходимое для повышения температуры тела на 1°, кал/град.; А - теплоотдача тела - количество тепла, рассеиваемое поверхностью тела в секунду при разности температур тела и среды в 1°, кал/сек · град.; - превышение температуры тела над температурой окружающей среды, в градусах. После интегрирования выражения (1) получаем: (2) Постоянная интегрирования может быть найдена из начальных условий: при t=1 начальный перегрев (3) Подставляя значение постоянной интегрирования в (2), получим: (4) Обозначая в равенстве (4) и , после несложных преобразований получим уравнение, определяющее закон изменения температуры перегрева электродвигателя от времени: (5) Если в начальный момент температура перегрева равна нулю, уравнение нагрева принимает следующий вид: (6) Из анализа уравнений (5) и (6) видно, что при , т.е. - это значение установившейся температуры перегрева, которое достигается электродвигателем по истечении бесконечно большого промежутка времени. Практически, установившейся температуры двигатель достигает за время, равное . - называется постоянной времени нагрева. Кривые нагрева, построенные по уравнения (5) и (6), представлены на рисунке 7.1. Уравнение, определяющее закон изменения температуры электродвигателя при охлаждении, можно получить из уравнения (5), если подставить в него вместо температуру перегрева, с которой начинается охлаждение , вместо - температуру, до которой охлаждается электродвигатель , а вместо Тн постоянную времени охлаждения Т0. После подстановки имеем: (7) В случае, когда охлаждение электродвигателя совершается до температуры окружающей среды , уравнение (7) приобретает вид: (8) Кривые охлаждения, построенные по уравнениям (7) и (8), представлены на рисунке 7.2.
Постоянная времени нагрева и методы ее определения
Из уравнений, определяющих закон изменения температуры электродвигателя, следует, что основной величиной, характеризующей процесс нагревания, является постоянная времени нагрева. Постоянная времени нагрева зависит от конструкции и размеров двигателя. Ее величина для двигателей защищенных, небольшой мощности, лежит в пределах 10-20 мин., а для крупных закрытых электродвигателей она достигает нескольких часов. Выражение постоянной времени нагрева ТН=С/А показывает, что ее значение зависит также и от условий вентиляции машины. Естественно, что у электродвигателей, имеющих более интенсивный отход тепла, постоянная времени нагрева меньше. Следует иметь в виду, что уменьшение скорости вращения вызывает увеличение постоянной времени нагрева, так как при этом ухудшаются условия вентиляции. Так постоянная времени нагрева у двигателей с самовентиляцией в неподвижном состоянии достигает четырехкратного значения постоянной нагрева при вращении. Аналитическое определение постоянной времени нагрева очень сложнои недостаточно точно. Поэтому её, как правило, определяют, пользуясь экспериментальными данными, в частности, из кривой зависимости превышения температуры от времени и установившегося значения температуры перегрева двигателя при номинальной нагрузке.
а) Определение Тн , исходя из её физического смысла. Постоянную времени нагрева можно представить как время, в течение которого превышение температуры машины, достигнет установившегося значения при отсутствии отдачи тепла в окружающую среду, т.е. при А=0. Уравнение теплового баланса (1) при этом будет иметь вид: . (9) Рассматривая случай, когда при t = 0, , после интегрирования получим: , (10) где . Подставляя значение установившейся температуры в равенство (10), получим: . В реальных условиях при наличии теплоотдачи, температура двигателя за время поднимется до значения, несколько меньшего . Величина этой температуры определится, если в уравнении (6) принять . При этом получим: Величиной 0,632 можно воспользоваться для определения постоянной времени нагрева при наличии опытной кривой . На кривой находится точка , из которой опускается перпендикуляр на ось абсцисс; отрезок времени, заключенный между началом координат и перпендикуляром, будет равняться постоянной времени нагрева. Определение Тн данным методом показано на рисунке 7.3.
б) Определение Тн с помощью касательной к кривой . Отрезок прямой , отсекаемый касательной и вертикалью, проведенной в точке касания, дает величину постоянной времени нагрева. Это легко доказывается, например, для касательной, проведенной из начала координат (рисунок 7.4). Для доказательства возьмем первую производную выражения (6) по времени: .
Для t=0 , а ; тогда . Из рисунка 7.4 видно, что , а , тогда Определение Тн с помощью касательной справедливо для любой точки кривой , но так как экспериментальная кривая несколько отличается от теоретической, то практически при определении постоянной времени нагрева берут среднее значение Тн из трех: в начале процесса, при и .
в) Определение Тн интегральным методом. В уравнении нагрева второй член правой части представляет собой для любого момента времени отрезок, заключенный между и кривой нагрева. Если взять интеграл от этой величины в пределах от t=0 до t=t1, то получим площадь S заключенную между кривой нагрева, осью ординат, асимптотой и вертикалью ab (рисунок 7.5). Действительно , но так как , то будем иметь , откуда .
Следовательно, для определения постоянной времени нагрева интегральным способом необходимо измерить при соответствующем учете масштабов площадь S и ее числовое значение разделить на . Этот метод определения Тн более точен по сравнению с предыдущим.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. До начала исследования необходимо ознакомиться с электрооборудованием установки и методом измерения температуры. 2. 3аписать паспортные данные электродвигателя. 3. Замерить температуру железа статора и обмотки статора в лобовой части, а также температуру окружающей среды. 4. Произвести пуск электродвигателя. 5. Установить номинальную нагрузку электродвигателя. 6. Через каждые пять минут замерять температуру железа, обмотки статора и окружающей среды. 7. По достижении установившейся температуры электродвигатель отключить от сети.
Рисунок 7.1
Рисунок 7.2
Рисунок 7.3
Элементы схемы (рисунок 7.6) М - приводной асинхронный электродвигатель, G1 – нагрузочный генератор, G2 - тахогенератор, SB1 и SB2 - кнопки «Стоп» и «Пуск» соответственно, KM1– линейный контактор, QF1, QF2 - автоматические выключатели, Rн– нагрузка.
Рисунок 7.4
Рисунок 7.5
ОФОРМЛЕНИЕ РАБОТЫ Для оформления работы требуется: 1. Вычертить принципиальную схему установки, привести данные машин и используемых приборов. 2. Построить кривые нагрева и охлаждения для обмотки статора в лобовой части, для железа статора. Рисунок 7.6
3. Определить постоянные времени нагрева и охлаждения обмотки статора тремя методами. 4. Рассчитать аналитическую кривую нагрева или охлаждения. 5. Дать заключения и выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Основные положения классической теории нагрева. 2. Понятие длительного режима работы электродвигателя. 3. Постоянная времени нагрева и методы её расчета. 4. Основные классы изоляционных материалов. Лабораторная работа №8 cyberpedia.su Нагревание и охлаждение идеального однородного твердого телаУравнение нагреванияХотя электрическая машина имеет сложное устройство, в основу анализа процесса ее нагревания может быть положена теория нагревания идеального однородного твердого тела, под которым здесь понимается тело, обладающее равномерным рассеянием тепла со всей поверхности и бесконечно большой теплопроводностью, вследствие чего все точки тела имеют одинаковую температуру. Составим дифференциальное уравнение нагревания такого тела, для чего рассмотрим его тепловой баланс. Пусть в единицу времени в теле выделяется количество теплоты Q. Тогда за бесконечно малый промежуток времени выделяемое количество теплоты будет равно Q × dt. Эта теплота частично аккумулируется в теле при повышении температуры и частично отдается во внешнюю среду. Если за время dt температура тела повысилась на dΘ, то количество аккумулируемой за это время теплоты равно G × c × dΘ, где G – масса тела и c – его удельная теплоемкость. Пусть в рассматриваемом бесконечно малом интервале времени превышение температуры тела над температурой окружающей среды равно Θ. Тогда количество теплоты, отдаваемое в окружающее пространство за время dt вследствие лучеиспускания, конвекции и теплопроводности, будет равно S × λ × Θ × dt, где S – площадь тела и λ – коэффициент теплоотдачи с поверхности. На основе закона сохранения энергии
Прежде чем приступить к решению уравнения нагревания (1), несколько преобразуем его. Установившееся превышение температуры и постоянная времени нагреванияПосле истечения достаточно длительного времени (теоретически при t = ∞) температура тела достигает установившегося значения. Тогда dΘ = 0 и Θ = Θ∞. Подставив эти значения в выражение (1), получим Q ×dt = S × λ × Θ∞ × dt , откуда
Установившееся превышение температуры Θ∞ тем больше, чем больше выделяется тепла и чем хуже условия ее отдачи, то есть чем меньше S × λ. Разделим обе части выражения (1) на S × λ, используем равенство (2) и обозначим
Тогда вместо (1) получим
Размерность всех членов (4) должна быть одинакова – температура, умноженная на время. Поэтому T имеет разность времени, что можно установить также по формуле (3). Величина T называется постоянной времени нагревания тела; согласно формуле (3), она тем больше, чем больше теплоемкость тела G × c и чем меньше интенсивность отдачи тепла, то есть меньше S × λ. Если определить из равенства (2) S × λ и подставить в (3), то получим еще одно выражение для T:
Числитель этого выражения равен количеству теплоты, накопленной в теле при достижении Θ = Θ∞. Следовательно, в соответствии с выражением (5) постоянная времени нагревания T равна времени, в течение которого температура достигла бы установившегося значения Θ∞, если бы отсутствовала передача тепла в окружающую среду и все выделяемое тепло накапливалось в теле. Решение уравнения нагреванияВ уравнении (4) можно разделить переменные и привести его к виду
При интегрировании уравнения (6) получим
Постоянная C определяется из начального условия: при t = 0 тело в общем случае имеет некоторое превышение температуры Θ = Θ0. Подставив указанные значения t и Θ в (7), найдем, что C = ln (Θ∞ – Θ0) . Подставим это значение C в (7) и переменим знаки. Тогда
откуда окончательно для Θ = f(t) находим
Случай нагревания при Θ0 = 0В этом случае вместо выражения (8) имеем
чему соответствует экспоненциальная кривая нагревания, изображенная на рисунке 1, а. При малых t, когда и Θ мало, теплопередача в окружающее пространство также мала, большая часть тепла накапливается в теле и температура его растет быстро, как это видно из рисунка 1, а. Затем с ростом Θ теплоотдача увеличивается и рост температуры тела замедляется. При t = ∞, согласно равенству (9), Θ = Θ∞. На рисунке 1, а указаны значения Θ, достигаемые через интервалы времени T, 2T, 3T и 4T. Из этого рисунка видно, что тело достигает практически установившегося превышения температуры через интервал времени t = 4T. Охлаждение телаЕсли тело имеет некоторое начальное превышение температуры Θ ≠ 0, но Q = 0 и, следовательно, в соответствии с выражением (2) Θ∞ = 0, то происходит охлаждение тела от Θ = Θ0 до Θ = Θ∞ = 0. Подставив в (8) Θ∞ = 0, получим уравнение охлаждения тела Экспоненциальная кривая охлаждения тела согласно уравнению (10) представлена на рисунке 1, б. Сначала, когда Θ и соответственно также теплоотдача велики, охлаждение идет быстро, а по мере уменьшения Θ охлаждение замедляется. При t = ∞ будет Θ = 0.
Рисунок 1. Кривые нагревания (а) и охлаждения (б) идеального однородного твердого тела Общий случай нагревания тела
Общий случай нагревания тела, описываемый уравнением (8), на основании формул (9) и (10) можно рассматривать как наложение двух режимов: 1) нагревания тела от начального превышения температуры Θ = 0 до Θ = Θ∞ и 2) охлаждения тела от Θ = Θ0 до Θ = 0. На рисунке 2 кривая 3 представляет собой кривую нагревания, построенную по уравнению (8). Эту кривую можно получить путем сложения ординат кривых 1 и 2, соответствующих уравнениям (9) и (10). Графический способ определения TНайдем подкасательную бв (рисунок 1, а), отсекаемую на асимптоте Θ = Θ∞ касательной к кривой Θ = f (t). Из рисунка 1, а следует, что
где α – угол наклона касательной к кривой Θ = f(t). Как известно,
Но, согласно выражению (6),
Подставив tg α из (12) в (11), получим бв = T . Таким образом, подкасательная к любой точке кривой нагревания или охлаждения равна постоянной времени нагревания T. Этим свойством кривых Θ = f(t) можно воспользоваться для графического определения T, если имеется кривая Θ = f(t), снятая, например, опытным путем. На рисунке 1, б и 2 показан способ определения T при построении касательной к начальной кривой. Заключительные замечанияВыше была изложена теория нагревания идеального однородного твердого тела. В действительности электрическая машина не представляет собой такого тела, так как она состоит из разных частей, обладающих конечной теплопроводностью, причем теплопроводность электрической изоляции достаточно мала. Поэтому отдельные части машины (обмотка, сердечники и другие) имеют различные температуры. В связи с этим более правильно было бы рассматривать электрическую машину как совокупность нескольких однородных тел, между которыми существует теплообмен. В действительных условиях величина T также не вполне постоянна, так как коэффициенты теплоотдачи зависят в определенной мере от температуры. Кроме того, воздух или другой охлаждающий агент при протекании по вентиляционным каналам нагревается, и поэтому температура охлаждающей среды для различных участков охлаждаемой поверхности имеет различные значения. Таким образом, кривые нагревания и охлаждения не являются, строго говоря, экспоненциальными. Однако в большинстве практических случаев мы не делаем существенных ошибок, считая их экспоненциальными, то есть применяя изложенную выше теорию нагревания идеального однородного тела. Источник: Вольдек А. И., "Электрические машины. Учебник для технических учебных заведений" – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с. www.electromechanics.ru Постоянные времени нагрева и охлажденияПостоянную времени нагрева – в уравнении (7-5) можно определить, подставив времяв (7-6а)
получим:
. Постоянная времени нагрева – это время, в течении которого превышение температуры двигателя над окружающей средой, при неизменных условиях работы, достигнет значения .[чилк353] Двигатель в процессе охлаждения, стремится к температуре окружающей среды – этот период может быть очень длительным. Для практических целей считают двигатель остывшим полностью, если его температура отличается от температуры окружающей среды не более чем на 3. Подставим в уравнение охлаждения:
и получим:
Постоянная времени охлаждения – это время, в течении которого превышение температуры двигателя над окружающей средой, при неизменных условиях работы, достигнет значения . Постоянные времени нагрева и охлаждения двигателя зависят от его массы, а следовательно и от мощности. Чек 302 28.02.13 321сп прогуи ТЕМА ЛЕКЦИИ 8 Классификация режимов работы судового электрооборудования в зависимости от продолжительности рабочего цикла План лекции
Судовое электрооборудование будет работать надежно, если оно не только правильно сконструировано, но и правильно используется.СЭО используется правильно, если оно соответствует условиям работы судового механизма, устройства и т.п. Поясним сказанное на примере условий работы электродвигателей. Например, электродвигатели насосов и вентиляторов работают с постоянной нагрузкой, при неизменном токе. В то же время электродвигатели грузоподъемных механизмов работают в более тяжелых условиях – с частыми пусками, сопровождающимися бросками тока. Ясно, что использовать в грузоподъемных механизмах электродвигатели, предназначенные для насосов или вентиляторов нельзя – они быстро сгорят. Если, наоборот, использовать для насосов или вентиляторов электродвигатели, предназначенные для грузоподъемных механизмов, можно, но нецелесообразно – они окажутся недоиспользованными по мощности, т.к. вместо работы в тяжелых условиях (с бросками токов) они станут работать в легких (с постоянной нагрузкой). Таким образом, каждому виду СЭО соответствует «свой», определенный режим работы. Тот или иной режим работы электрооборудования полностью зависит от технологических условий работы. То есть, механизм «навязывает» электрооборудованию (например, электродвигателю) свои условия работы – как работает механизм, так должен работать и электродвигатель. Приведем основные сведения, связанные с понятием «режим работы электрооборудования», применительно к электродвигателям. Это объясняется тем, что основную часть производимой на судне электроэнергии (до 85…90%) потребляют именно электродвигатели. studfiles.net | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|













 на τу — τi, получим в системе координат Δτ и τу — τi уравнение прямой проходящей через начало координат:
на τу — τi, получим в системе координат Δτ и τу — τi уравнение прямой проходящей через начало координат:
 представляет собой угловой коэффициент. Отсюда следует, что точки kΔτi, kΔτi+1 и другие будут лежать на одной прямой.
представляет собой угловой коэффициент. Отсюда следует, что точки kΔτi, kΔτi+1 и другие будут лежать на одной прямой.







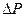 , которые складываются из магнитных потерь (в стали),электрических потерь (потерь в меди), а также механических потерь. За время
, которые складываются из магнитных потерь (в стали),электрических потерь (потерь в меди), а также механических потерь. За время 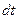 двигатель с потерями мощности равными
двигатель с потерями мощности равными 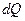 . Это тепло во первых расходуется на нагревание самого двигателя:
. Это тепло во первых расходуется на нагревание самого двигателя: (99)
(99)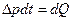 (100)
(100)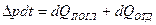 (101)
(101)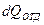 и при некоторой температуре двигателя наступает установившийся режим, после чего всё выделяемое при работе тепло рассеивается в окружающую среду., а температура двигателя при условии неизменности нагрузки на его валу в дальнейшем не меняется. Необходимо отметить, что реальные термодинамические процессы в ЭП носят весьма сложный характер, т.к. эл. машины во первых не однородна по материалу, во вторых имеет рассредоточенные внутренние источники тепла, интенсивность которых зависит от режима, скорости и т.д. Поэтому для дальнейшего анализа тепловых переходных процессах в ЭП, применим следующие допущения:
и при некоторой температуре двигателя наступает установившийся режим, после чего всё выделяемое при работе тепло рассеивается в окружающую среду., а температура двигателя при условии неизменности нагрузки на его валу в дальнейшем не меняется. Необходимо отметить, что реальные термодинамические процессы в ЭП носят весьма сложный характер, т.к. эл. машины во первых не однородна по материалу, во вторых имеет рассредоточенные внутренние источники тепла, интенсивность которых зависит от режима, скорости и т.д. Поэтому для дальнейшего анализа тепловых переходных процессах в ЭП, применим следующие допущения: и с одинаковой температурой по всём точном объема тела.
и с одинаковой температурой по всём точном объема тела.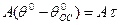 (102)
(102) - теплоотдача
- теплоотдача - температура двигателя в градусах
- температура двигателя в градусах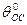 - температура окружающей среды
- температура окружающей среды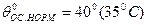
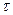 - превышение температуры
- превышение температуры 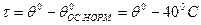
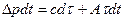 (103)
(103) -потери мощности в двигателе
-потери мощности в двигателе -изменение превышения температуры
-изменение превышения температуры все члены уравнения 103 на
все члены уравнения 103 на 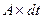 , то
, то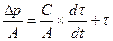 (104)
(104)
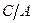 (сек) обозначим
(сек) обозначим 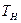 - постоянна времени нагрева,то с учётом этого уравнение (104) будет иметь вид:
- постоянна времени нагрева,то с учётом этого уравнение (104) будет иметь вид: (105)
(105)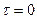 до
до 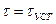 . Решение этого уравнения имеет вид:
. Решение этого уравнения имеет вид:
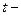 текущее время (с).
текущее время (с).
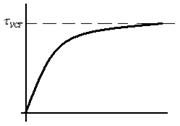
 , а затем выключить из питающей сети, то процесс его охлаждения до температуры окружающей среды может быть представлен в виде уравнения которое носит название решение уравнения теплового баланса при охлаждении и имеет следующий вид:
, а затем выключить из питающей сети, то процесс его охлаждения до температуры окружающей среды может быть представлен в виде уравнения которое носит название решение уравнения теплового баланса при охлаждении и имеет следующий вид: (106)
(106) - постоянная времени охлаждения она имеет такой же физический смысл что и постоянная времени нагрева, но в силу того, что в термодинамике процессы охлаждения имеют несколько большую инерционность, чем процессы нагрева для одного и того же двигателя, находятся примерно в таком соотношении:
- постоянная времени охлаждения она имеет такой же физический смысл что и постоянная времени нагрева, но в силу того, что в термодинамике процессы охлаждения имеют несколько большую инерционность, чем процессы нагрева для одного и того же двигателя, находятся примерно в таком соотношении:
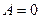 , то
, то (107)
(107)

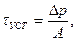 получим, что
получим, что 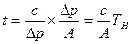 .
.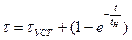 (108)
(108) , тогда:
, тогда: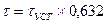
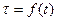 .
.
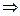
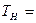 1-й степени габаритов двигателя и определение номинальной мощности двигателя малой мощности (до 100кВт) открытого исполнения постоянной времени нагрева находиться в пределах 1 минуты
1-й степени габаритов двигателя и определение номинальной мощности двигателя малой мощности (до 100кВт) открытого исполнения постоянной времени нагрева находиться в пределах 1 минуты 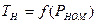 при
при 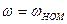 имеет следующий вид:
имеет следующий вид: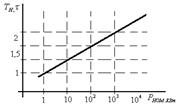
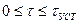 зависит от нагрузки на валу двигателя (
зависит от нагрузки на валу двигателя (  - механической мощности), чем больше нагрузка, тем двигатель нагревается быстрее. Однако при этом будет изменяться величина установившейся температуры. Зависимость
- механической мощности), чем больше нагрузка, тем двигатель нагревается быстрее. Однако при этом будет изменяться величина установившейся температуры. Зависимость