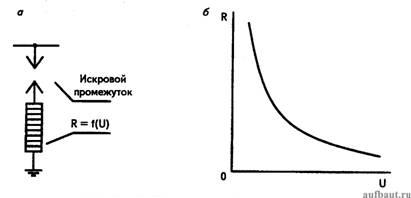
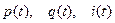Закон Ома для переменного тока. Переменного тока формулыГенераторы переменного тока | Формулы и расчеты онлайнЕсли для получения электрического напряжения используется прополочная рамка, вращающаяся в магнитном поле, то напряжение индукции не постоянно, а зависит от мгновенного положения рамки в магнитном поле. 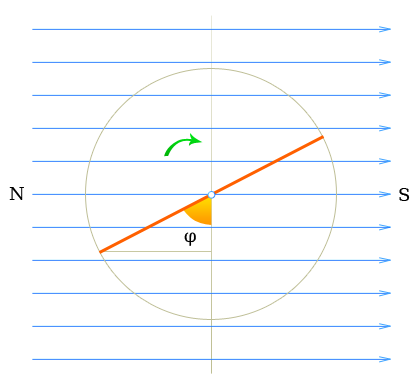 Генераторы переменного тока В соответствии с формулой №1 напряжение индукции пропорционально скорости изменения магнитного потока. Согласно выражению \[ Φ = BS \] , магнитный поток пропорционален площади сечении магнитного поля, пересекающего рамку, т.е. \[ Φ = B · S · \cos(φ) \] Аналогичное выражение справедливо для вращающейся катушки. Если
то \[ u= - N \frac{dФ}{dt} \] \[ u= - \frac{d(NBS \cos(φ))}{dt} \] \[ u= - \frac{d(NBS \cos(ωt))}{dt} \] откуда Переменное напряжение\[ u = NBS ω \sin(ωt) \] Переменное напряжение Напряжение индукции меняется во времени по синусоидальному закону. В течение периода оно дважды меняет знак. Поэтому его называют переменным напряжением. Амплитуда, или максимальное значение напряжения индукции, определяется формулой \[ U_{m}= NBSω \] Тогда для мгновенного напряжения имеем \[ u = U_{m} \sin(ωt) \] \[ u = U_{m} \sin(2πft) \] \[ u = U_{m} \sin(2π\frac{t}{T}) \] Величина ω=2πf называется угловой частотой. Частота переменного тока промышленной сети f = 50 Гц, и соответственно ω = 100π 1/с. Переменный токЕсли к клеммам вращающейся катушки присоединить внешнюю электрическую цепь, то в ней возникает электрический ток, сила которого изменяется по синусоидальному закону во времени и меняет свой знак (направление) дважды за период. Такой ток называется переменным током. Если
то то по аналогии получаем \[ i = I_{m} \sin(ωt) \] \[ i = I_{m} \sin(2πft) \] \[ i = I_{m} \sin(2π \frac{t}{T}) \] График зависимости напряжения u от времени t (или от φ = ωt) представляет собой синусоиду. 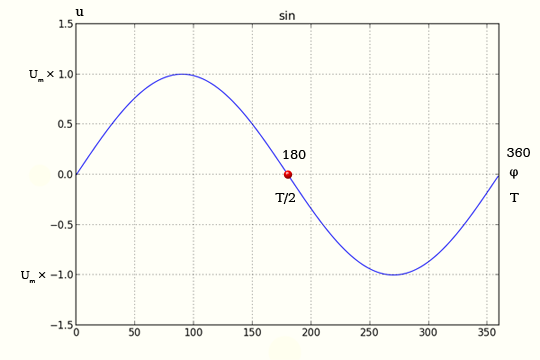 Переменное напряжение В любом генераторе переменного тока имеются магнит, создающий требуемое магнитное поле (чаще всего электромагнит; в генераторах малой мощности используются постоянные магниты), вращающиеся обмотки и контактные кольца. Для получения достаточно высокого напряжения применяют обмотки с большим числом витков и железные сердечники. Вращающаяся часть генератора называется ротором, неподвижная часть — статором. 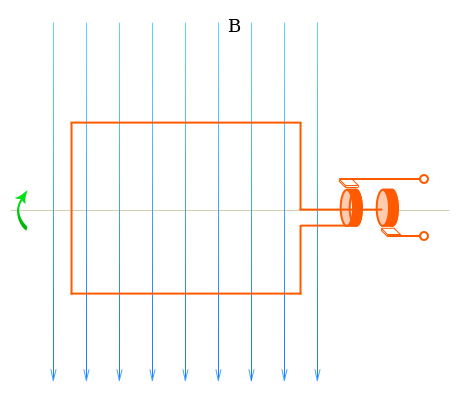 генератор переменного тока В генераторах большой мощности обмотки, в которых индуцируется напряжение, располагаются на статоре, а магниты — на роторе (машина с внутренними полюсами). При этом контактные кольца служат лишь для подвода небольшой мощности к электромагнитам. В помощь студенту
www.fxyz.ru Расчетные формулы для цепей переменного токаРасчет цепей переменного тока. В таблице ниже представлены основные расчетные формулы цепей переменного тока. Формулы для переменного тока.
www.eti.su Закон Ома для переменного тока: формулаСодержание:
Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи. Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов. Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи. Закон ома для участка цепиЗакон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока. В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах. Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно. Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке. Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение. Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга. Если они расположены на одном уровне, то их нужно перемножить, а если на разных – верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам. Закон ома для полной цепиМежду отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами. Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока. Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта. Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания. Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R. Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока. По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами. Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов. Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела. Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r). На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е. Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U < E. ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока. В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы. Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода. Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка. Закон ома для цепи переменного токаДля цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты. Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет. Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится. Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс. Для обозначения полного сопротивления контура используется символ Z. Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура. electric-220.ru Переменный синусоидальный ток
Колебания маятника также подчиняются закону синуса. Если записать проекцию траектории движения математического маятника на движущуюся бумажную ленту — получится синусоида. Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по закону синуса. Синусоидальный ток — элементарный, то есть его невозможно разложить на другие более простые переменные токи. Переменный синусоидальный ток выражается формулой: , где — амплитуда синусоидального тока; — некоторый угол, называемый фазой синусоидального тока. Фаза синусоидального тока изменяется пропорционально времени . Множитель , входящий в выражение фазы — величина постоянная, называемая угловой частотой переменного тока. Угловая частота синусоидального тока зависит от частоты этого тока и определяется формулой: , где — угловая частота синусоидального тока; — частота синусоидального тока; — период синусоидального тока; — центральный угол окружности, выраженный в радианах. Зависимость синусоидального тока от времени Зависимость синусоидального тока от угла ωt Периоду соответствует угол , половине периода угол и так далее… Исходя из формулы , можно определить размерность угловой частоты: , где — время в секундах, — угол в радианах, является безразмерной величиной. Фаза синусоидального тока измеряется радианами. 1 радиан = 57°17′, угол 90° = радиан, угол 180° = радиан, угол 270° = радиан, угол 360° = радиан, где радиан; — число «Пи», ° — угловой градус и ′ — угловая минута.
Формула описывает случай, когда наблюдение за изменением переменного синусоидального тока начинается с момента времени при . Если не равен нулю, тогда формула для определения мгновенного значения переменного синусоидального тока примет следующий вид: , где — фаза переменного синусоидального тока; — угол, называемый начальной фазой переменного синусоидального тока. Начальная фаза переменного тока Начальная фаза переменного тока Если в формуле принять , то будем иметь , и . Начальная фаза — это фаза синусоидального тока в момент времени . Начальная фаза переменного синусоидального тока может быть положительной или отрицательной величиной. При мгновенное значение синусоидального тока в момент времени положительно, при — отрицательно. Если начальная фаза , то ток определяется по формуле . Мгновенное значение его в момент времени равно , то есть равно положительной амплитуде тока. Если начальная фаза , то ток определяется по формуле . Мгновенное значение его в момент времени равно , то есть равно отрицательной амплитуде тока. 9. Идеальные элементы электрической цепи синусоидального тока 11. Неразветвленная цепь синусоидального тока. Резонанс напряжений Резонанс напряжений - резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура. Описание явленияПусть имеется колебательный контур с частотой собственных колебаний f, и пусть внутри него работает генератор переменного тока такой же частоты f. В начальный момент конденсатор контура разряжен, генератор не работает. После включения напряжение на генераторе начинает возрастать, заряжая конденсатор. Катушка в первое мгновение не пропускает ток из-за ЭДС самоиндукции. Напряжение на генераторе достигает максимума, заряжая до такого же напряжения конденсатор. Далее: конденсатор начинает разряжаться на катушку. Напряжение на нем падает с такой же скоростью, с какой уменьшается напряжение на генераторе. Далее: конденсатор разряжен до нуля, вся энергия электрического поля, имевшаяся в конденсаторе, перешла в энергию магнитного поля катушки. На клеммах генератора в этот момент напряжение нулевое. Далее: так как магнитное поле не может существовать стационарно, оно начинает уменьшаться, пересекая витки катушки в обратном направлении. На выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе противоположного знака, причем с той же скоростью, с какой катушка заряжает конденсатор. Далее: катушка перезарядила конденсатор до максимального напряжения. Напряжение на генераторе к этому моменту тоже достигло максимального. Возникла следующая ситуация. Конденсатор и генератор соединены последовательно и на обоих напряжение, равное напряжению генератора. При последовательном соединении источников питания их напряжения складываются. Следовательно, в следующем полупериоде на катушку пойдет удвоенное напряжение (и от генератора, и от конденсатора), и колебания в контуре будут происходить при удвоенном напряжении на катушке. В контурах с низкой добротностью напряжение на катушке будет ниже удвоенного, так как часть энергии будет рассеиваться (на излучение, на нагрев) и энергия конденсатора не перейдет полностью в энергию катушки). Соединены как бы последовательно генератор и часть конденсатора. studfiles.net Закон Ома для переменного тока
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него. Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы). В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.
Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю. Тогда, падение напряжения на активном сопротивлении определяется по формуле:
где, U-напряжение на элементе цепи, I – ток через элемент цепи R – активное сопротивление элемента Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
где, Um-амплитудное значение напряжения на элементе цепи, Im – амплитудное значение тока через элемент цепи R – активное сопротивление элемента В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).
Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.
Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов. Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения. Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
где — UL-падение напряжение на чисто индуктивном сопротивлении ; UС—падение напряжения на чисто емкостном сопротивлении; I— значение тока в через реактивное сопротивление; L— индуктивность реактивного элемента; C— емкость реактивного элемента; ω— циклическая частота. Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов. Приведенные выше формулы являются частными случаями закона Ома для переменного тока. Следовательно, полный закон Ома для переменного тока будет иметь вид:
Где Z – полное сопротивление цепи переменного тока. Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены. Закон Ома для различных типовых цепей переменного токаДавайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)
Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления. Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:
где —эффективное значение силы тока в А; U—эффективное значение напряжения в В; R—активное сопротивление в Ом; ωL—индуктивное сопротивление в ом. Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения. В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.
Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления. А закон Ома для такой цепи принимает вид:
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),
Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления. Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:
где I-сила тока в А; U-напряжение в В; R-активное сопротивление в Ом; ωL-индуктивное сопротивление в Ом; 1/ωС-емкостное сопротивление в Ом. Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения. Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).
Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) - параллельное соединение R и L; б) - параллельное соединение R и C.
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.
Рисунок 8. Эквивалентная схема колебательного контура.
Таким образом закон Ома для переменного тока можно сформулировать следующим образом. Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! Похожие материалы:Добавить комментарийwww.sxemotehnika.ru Переменный электрический токПеременный ток – или AC (Alternating Current). Обозначение ( ~ ). Электрический ток называется переменным, если он в течение времени меняет свое направление и непрерывно изменяется по величине. Переменный ток, который используется для подключения бытовых или производственных электрических приборов, изменяется по синусоидальному закону:
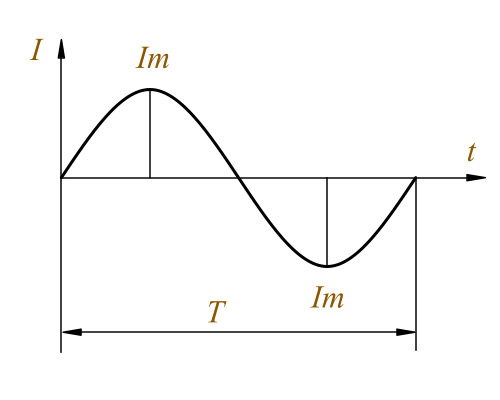 График переменного тока
Широко используется переменный ток благодаря тому, что электроэнергия переменного тока технически просто и экономно может быть преобразована из энергии более низкого напряжения в энергию более высокого напряжения и наоборот. Это свойство переменного тока позволяет передавать электроэнергию по проводам на большие расстояния. 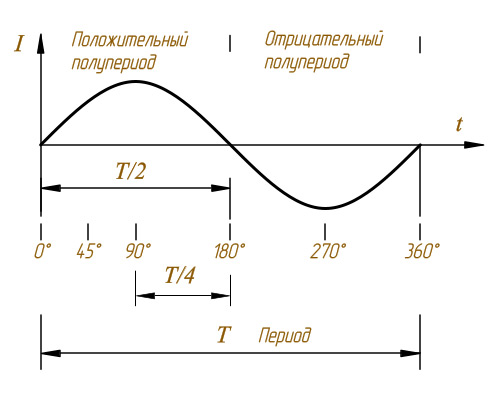 Период переменного тока
Промышленный переменный электрический ток получают при помощи электрических генераторов, принцип работы которых основан на законе электромагнитной индукции. Вращение генератора осуществляется механическим двигателем, использующим тепловую, гидравлическую или атомную энергию. Переменный однофазный электрический ток имеет следующие основные характеристики: f – частота переменного тока определяет количество циклов или периодов в единицу времени. За единицу измерения частоты переменного тока принят Герц ( Гц ): 1гц = 103кгц = 106мгц Τ – период – время одного полного изменения переменной величины. Если в 1 секунду происходит 1 период Τ, то частота f = 1 Гц ( Герц ). 1c = 103мс = 106мкс = 1012нс В Российской Федерации период Τ переменного тока принят равным 0,02 секунды,следовательно по формуле f = 1/Τ можно определить частоту переменного тока: f = 1/0,02 = 50 Гц ω – угловая скорость Помимо частоты f при изучении цепей переменного тока вводится понятие угловой скорости ω. Угловая скорость ω связана с частотой f следующим соотношением: ω=2πf При частоте 50 Гц угловая скорость равна 314 рад/с (2 × 3,14 × 50 = 314). Мгновенное значение (i,u,e,p) – значение величины в данный момент, мгновенное. Максимальное или амплитудное значение (Im,Um,Em,Pm). Эффективное значение тока – это величина переменного тока, равная такому току, который на сопротивлении R, создаёт тепловыделение равное данному переменному току, за тоже время t (I,U,E,P). Получение синусоидальной кривойВ системе декартовых прямоугольных координат совмещены тригонометрический круг и кривая, отражающая изменение величины тригонометрической функции sinβ от величины угла β между осью 0х и радиусом-вектором r. Радиус-вектор r вращается против часовой стрелки. Повернем радиус-вектор на угол β и от конца вектора r проведем пунктиром прямую, параллельную оси 0х. От окружности (точка а) по оси 0х отложим в масштабе отрезок. Из конца отрезка построим перпендикуляр до пересечения с пунктирной прямой. Получим точку с в пересечении перпендикуляра и пунктирной прямой. 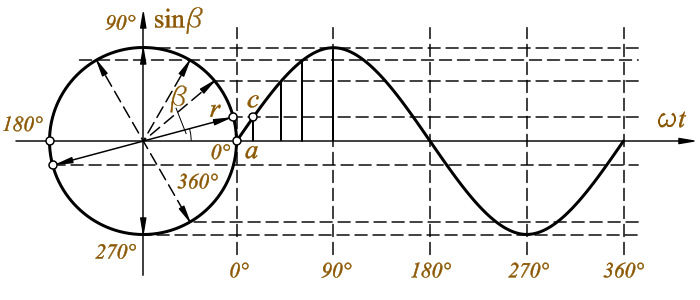 Синусоида переменного тока Аналогичное построение проведем, увеличивая угол β, пока радиус-вектор повернется на угол β = 360°, и получим точки аналогично точке с. Соединим точки плавной кривой, которая и будет отражать синусоидальный закон изменения величины переменного тока. Понятие о фазеЕсли две переменные величины одновременно проходят свои нулевые и максимальные значения, то они совпадают по фазе. Если две переменные величины не одновременно проходят свои нулевые и максимальные значения, то они не совпадают по фазе. В радиотехнике используются понятия:
1. Активное сопротивление ( Ra ) 2. Индуктивное сопротивление ( XL – реактивное сопротивление ) 3. Ёмкостное сопротивление ( XC – реактивное сопротивление ) Понятие об активном сопротивленииЕсли по проводнику протекает ток, то вследствие явления самоиндукции, электроны распространяются не равномерно по сечению проводника, вследствие чего растёт сопротивление проводника. Явление неравномерного распространения зарядов по сечению проводника называется – поверхностный эффект. Чем больше частота, тем больше сопротивление. selectelement.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|















 или
или 


 или
или 


 или
или 


 или
или 


 или
или