Потери мощности электроэнергии в электрических сетях. От чего зависит потеря мощности в лэпПотери мощности и энергии в линиях электропередачи⇐ ПредыдущаяСтр 4 из 6Следующая ⇒При прохождении электрического тока по проводам воздушных и кабельных линий, внутренних электропроводок происходит нагрев проводов и выделение тепла согласно закону Джоуля-Ленца. Часть электроэнергии, переходящая при этом в тепло, называют потерями энергии. Потери мощности и энергии должны быть компенсированы генераторами электростанций, что увеличивает их нагрузку и требует дополнительного расхода топлива. Расчет потерь мощности и энергии важен как при проектировании, так и при эксплуатации линий электропередач и подстанций. Потери активной мощности в линии определяется ее сопротивлением и нагрузкой. В зависимости от того, какими параметрами определяется нагрузка, потери мощности могут быть рассчитаны по одной из следующих формул:
Если нагрузка в течение времениТ остается неизменной, то потери энергии составляют:
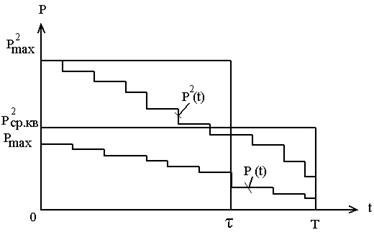
В действительности нагрузка изменяется в соответствии с графиком, при этом потери мощности пропорциональны квадрату нагрузки. На практике используют специальные характеристики графика нагрузки для расчета потерь энергии. Так как потери энергии рассчитывают за длительный период (месяц, год), то эти характеристики относят к графику нагрузки по продолжительности.
Если мощность на каждой ступени графика возвести в квадрат, то получим график квадратичной функции нагрузки Р2(t). Площадь, ограниченная квадратичной функцией, пропорциональна потерям энергии в линии за период Т. При неизменной нагрузке Рср.квза времяТ потери энергии в линии составят такую же величину, что и при реальном графике. Таким образом, потери энергии могут быть определены по среднеквадратичной нагрузке линии за период времениТ:
Среднеквадратичная мощность может быть определена по средней мощности и коэффициенту формы графика PСК = PСР∙kф ; для реальных графиков нагрузки в сельских сетях kФ = 1,05…1,15. Другой эквивалентной характеристикой графика является время потерь τ. При этом потери энергии могут быть определены по максимальной нагрузке линии и времени τ:
На практике время потерь определяют по графикам в зависимости от времени использования максимума Tmax. Для сельских сетей Tmax составляет 1000–3000 час, при этом τ соответственно 800–2500 час.
Потери мощности и энергии в трансформаторах В силовых трансформаторах токи, проходящие по обмоткам, также вызывают их нагрев и обуславливают потери энергии. Кроме того, переменный магнитный поток в сердечнике трансформатора является причиной потерь энергии на перемагничивание стали и вихревые токи (нагрев сердечника). В схеме замещения трансформатора потери в обмотках отражены активным сопротивлением RT, а потери в сердечнике (потери в стали) – активной проводимостью GT. Потери в сердечнике определяются квадратом напряжения и проводимостью трансформатора; потери в обмотках пропорциональны току нагрузки и определяются аналогично потерям в линии. Таким образом, суммарные потери:
Если напряжение считать номинальным, а параметры RТ и GT определить через паспортные данные трансформатора, получим:
Таким образом, можно считать, что потери активной мощности в трансформаторе состоят из двух составляющих, одна из которых (потери в сердечнике) неизменна при любой нагрузке, другая (потери в обмотках) – зависит от квадрата коэффициента загрузки трансформатора. При определении потерь энергии в трансформаторе постоянные потери мощности надо умножить на времяТграфика, а переменные потери при максимальной нагрузке – на время потерь:
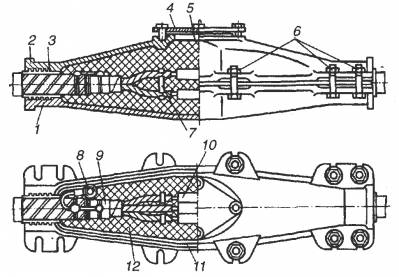
Напряжения на участке сети Режим напряжении 3-х фазной линии проиллюстрирован на рисунке. Если учитывать реальные параметры линии RЛ и XЛто и фазные и линейные напряжения в конце электропередачи отличаются от соответствующие напряжений в начале. По модулю напряжения в конце линии всегда меньше, чем в начале, а фаза их зависит от соотношений активной и индуктивной составляющих сопротивлений линии и нагрузки.
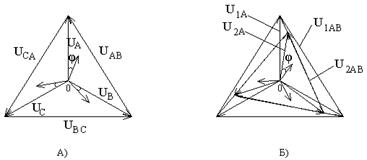
Векторные диаграммы 3-х фазной линии электропередачи без учета (а) и с учетом (б) сопротивления линии. На рисунке (а) приведена однолинейная схема электропередачи, а на рисунке (б) – векторная диаграмма одной из фаз.
а)
б) На векторной диаграмме отложены фазное напряжение в конце линии Потеря напряжения – это разность модулей Отрезок af называется продольной составляющей падения напряжения. Из геометрических сообщений. Отрезок cf называется поперечной составляющей падения напряжения. Продольная и поперечная составляющая обозначаются
Модули напряжений в начале и конце линии могут быть связаны: Фазовый сдвиг между ними определяется: В реальной сети величина вектора
Величина Читайте также: lektsia.com Потери мощности электроэнергии в электрических сетяхГлава 5. Потери мощностии электроэнергии в электрических сетях 5.1. Потери мощности в линиях Потери активной мощности в линиях обусловлены активными сопротивлениями проводов и кабелей, а также потерями на корону в воздушных линиях и на токи утечки через изоляцию в кабельных линиях высоких напряжений. В трехфазной линии, где нагрузка задана в виде полного тока Если нагрузка задана в виде полной Как видно, величина потерь зависит от передаваемой мощности и уровня напряжения. Повышение уровня напряжения позволяет снизить потери активной мощности в сопротивлении линии. Однако следует заметить, что при повышении напряжения в сетях, непосредственно питающих электроприемники, в соответствии со статическими характеристиками нагрузки по напряжению (см.§ 4.5) может увеличиться мощность потребителей и значит передаваемая по линии мощность. Мощность, передаваемая по линии, включает активную и реактивную составляющие. Если единственным источником активной мощности являются генераторы электрических станций, то реактивная мощность вырабатывается различными устройствами. Причем некоторые из них (компенсирующие устройства) могут устанавливаться вблизи потребителей реактивной мощности. Рассмотрим линию (рис.5.1), по которой передается мощность
Установим в конце линии, например, батарею конденсаторов мощностью
Снижение потерь активной мощности составит Количественной характеристикой эффективности снижения потерь мощности от компенсации реактивной мощности служит экономический эквивалент реактивной мощности Он показывает, на сколько снижаются потери активной мощности при включении в узле нагрузки компенсирующего устройства величиной В воздушных линиях высокого напряжения имеют место потери активной мощности на корону, которые в линиях напряжением 330 кВ и выше определяют по выражению (4.10). Как отмечалось, величина удельных потерь на корону Зависимость усредненных потерь мощности на корону от напряжения имеет вид где U – напряжение, В. Таким образом, при повышении уровня напряжения потери активной мощности на корону увеличиваются, но одновременно уменьшаются потери активной мощности в сопротивлении линии. Для кабелей высокого напряжения потери активной мощности, вызванные токами утечки через изоляцию, можно рассчитать по их активной проводимости Наряду с потерями активной мощности в линиях электропередачи теряется и реактивная мощность. Эти потери обусловлены индуктивными сопротивлениями воздушных и кабельных линий . Если нагрузка линии задана током, то потери реактивной мощности можно найти по формуле Для нагрузки, заданной мощностью, потери реактивной мощности в линии равны Наряду с потреблением реактивной мощности линия, обладая емкостной проводимостью и соответствующей ей зарядной мощностью vunivere.ru Определение потерь мощности в лэпДля определения потерь мощности в линии электропередачи следует определить параметры схемы замещения.
Рисунок 2 – «П»-образная схема замещения линии электропередачи Таблица 6 – Расчет параметров «П»-образной схемы замещения линии электропередачи
Таблица 7 – Расчетные формулы потерь в элементах схемы замещения ЛЭП
РАСЧЕТ ПРОИЗВЕСТИ НА ВСЕ РЕЖИМЫ. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИВЕСТИ ТАБЛИЧНО. ПОКАЗАТЬ ЧИСЛЕННЫЙ РАСЧЕТ ОДНОГО ИЗ РЕЖИМОВ. Определение уровня напряжения на шинах понижающей подстанцииВ режимах максимальных нагрузок и минимальных нагрузок напряжение на шинах источника питания определяется по выражению , кВ где - отклонение напряжения на шинах, смотри задание пункт 2.8. Падение напряжение до шин ВН трансформатора определяется как , кВ Уровень напряжения , кВ РАСЧЕТ ПРОИЗВЕСТИ НА ВСЕ РЕЖИМЫ. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИВЕСТИ ТАБЛИЧНО. ПОКАЗАТЬ ЧИСЛЕННЫЙ РАСЧЕТ ОДНОГО ИЗ РЕЖИМОВ. Выбор рабочих ответвлений понижающего трансформатора определение уровня напряжения на шинах сн и нн трансформатораТаблица 8 – Уровень напряжения на шинах потребителей приведенное к высокой стороне трансформатора
РАСЧЕТ ПРОИЗВЕСТИ НА ВСЕ РЕЖИМЫ. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИВЕСТИ ТАБЛИЧНО. ПОКАЗАТЬ ЧИСЛЕННЫЙ РАСЧЕТ ОДНОГО ИЗ РЕЖИМОВ. Таблица 9 – Определение реального значения уровня напряжения на шинах потребителей
РАСЧЕТ ПРОИЗВЕСТИ НА ВСЕ РЕЖИМЫ. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИВЕСТИ ТАБЛИЧНО. ПОКАЗАТЬ ЧИСЛЕННЫЙ РАСЧЕТ ОДНОГО ИЗ РЕЖИМОВ. studfiles.net Потери мощности в участке сетиРассмотрим участок сети, схема замещения которого показана на рис. 5.1. Обозначения, принятые на рисунке, следующее: — сопротивление, — проводимости схемы замещения, которые считаем заданными; — поток трехфазной мощности нагрузки, если в конце участка подключен потребитель, имеющий индуктивный характер, то . Аналогично для потока мощности, втекающей в сеть . Везде рассматриваются линейные напряжения и фазные токи. Начало и конец участка обозначены «н» и «к», ; . (5.1) Здесь и - соответственно потоки мощности в начале и конце сопротивления Z. , (5.2) с учетом того, что ,,, , где , — потери мощности в шунтах схемы замещения. Потери мощности в шунтах (5.2) не зависят от токов (потоков), передаваемых через участок сети, поэтому называются постоянными потерями. На основании первого закона Кирхгофа для узлов 1 и 2 можно записать ; . (5.3) Напротив, потери мощности в сопротивлении Z пропорциональны квадрату тока (потока), поэтому они называются переменными потерями. Для их определения используются следующие соотношения: . (5.4) Учитывая, что , имеем . (5.5) Так как ; , a , то выражение для переменных потерь мощности может быть представлено в различных формах, например ; . Следует обратить внимание, что потери мощности могут быть определены по данным как начала, так и конца участка — важно использовать напряжения и потоки мощности для одной и той же точки участка («к» или «н»). Для связи потоков и потерь можно использовать следующие выражения: ; (5.6) . (5.7)
Линия электропередачи имеет схему замещения, такую, как изображена на рис. 5.1, где ; . Тогда потери в шунтах линии, имеющих емкостный характер, равны . (5.8) Активные потери в шунтах определяются потерями на корону, а реактивная составляющая определяется емкостной генерацией линии. Обычно для расчетов потери активной мощности на корону в ЛЭП принимают равными средним удельным потерям и определяют из справочников [5, табл. 7.7]. С учетом числа параллельных линийп и длины ЛЭП потери в шунтах . Переменную составляющую потерь мощности можно определить по введенным ранее формулам (5.5). В приближенных расчетах, когда неизвестны точные значения напряжений в узлах электрической сети, потери мощности можно определять по приближенным (средним) значениям напряжений U.
Схема замещения двухобмоточного трансформатора отличается от схемы замещения рис. 5.1 только тем, что , поэтому введенные ранее выражения для вычисления потерь также справедливы для трансформаторов. Для приближенных расчетов постоянную составляющую потерь в трансформаторе (потери в стали ) можно считать равной потерям холостого хода. При этом предполагается, что напряжение на трансформаторе примерно равно номинальному. Для подстанции с п параллельными трансформаторами эквивалентные потери . (5.9) Если учитывать отклонение напряжения от номинального, то следует записать . (5.10) Переменная составляющая активных потерь в п параллельно включенных трансформаторах (потери в меди) в соответствии с (5.4) может быть определена по формуле . Учитывая, что для двухобмоточных трансформаторов , а , получаем . (5.11) Полагая в приближенных расчетах , имеем . (5.12) При определении потерь мощности в трехобмоточных трансформаторах и автотрансформаторах следует учитывать загрузку каждой из обмоток трансформаторов и потери короткого замыкания каждой из обмоток: , (5.13) где п — число трансформаторов; , ,— потоки мощности по обмоткам высшего, среднего и низшего напряжения соответственно; ,,— потери короткого замыкания обмоток;— номинальная мощность трансформатора. studfiles.net 5. Определение потерь мощности и энергии в линии электропередачи. Расчёт параметров электрической сетиПохожие главы из других работ:Изоляция высоковольтных линий электропередач 2.1 Определение параметров воздушной линии электропередачиДля проведения дальнейших расчетов необходимо рассчитать следующие параметры ВЛ: индуктивности, емкости, волновое сопротивление и волновую длину линии прямой последовательности... Конденсационная паровая турбина типа К-6-4 3.6.3 Определение потерь энергии, к.п.д. и внутренней мощности101.Выходная кинетическая энергия потока, покидающего ступень ?hc2 = C22/2 = 43,0732/2 = 0,928 кДж/кг; 102.Коэффициент использования выходной кинетической энергии в следующей ступени мi = 0,940; 103.Доля выходной кинетической энергии... Натуральная мощность линии 4. Линии электропередачи схемы выдачи мощностиДля сети 110 кВ и выше - достаточность пропускной способности ЛЭП, исходя из натуральной мощности линий, значений коэффициента К=1,4 для ВЛ 110(157) кВ, К=1,2 для ВЛ 220 кВ и К=1 для ВЛ 330 кВ и выше, ограничения наибольшей допустимой длины ЛЭП... Основные показатели работы электроэнергетической системы 2.3 Выполним расчет режима работы для линии электропередачи, отходящей от генератора Г2, автотрансформатора АТ и нагрузки Н1 при заданной для максимального режима активной мощности и трех значениях реактивной мощности генератора Г2. И построим зависимости напряжения на приемном конце линии ВЛ2, пот1) Находим потери мощности и напряжения на ВЛ2, а также мощность и напряжение в конце линии: S12=P21+j*Q2-ДSл2+j*Qзар2=930+j*697,5-19,612-j*298,106+j*364=910,388+j*763,394 МВА U12=U2-ДU13,12=525-87,863-j*102,389=437,137-j*102,389 кВ; | U12| =448,968 кВ Sат1в=S12-ДSат1в=910,388+j*763,394-0,896-j*113,796=909,491+j*649... Планирование режима работы основной электрической сети энергосистемы "Д" с учетом потерь на корону ЗАВИСИМОСТЬ ПОТЕРЬ НА КОРОНУ ОТ НАПРЯЖЕНИЯ ДЛЯ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ ПРИ ЗАДАННЫХ МЕТЕОУСЛОВИЯХРассматриваемая схема электросети имеет напряжения 330, 110, 35, 10 кВ. Очевидно, что потери на корону будут наблюдаться особенно сильно на проводах АС 2х300 номинальным напряжением 330 кВ. Исходя из рисунков 3.2, 3.4 - 3.6... Расчет питающей электрической сети 5. Определение сечений и выбор типа проводников линии электропередачиПри проектировании воздушных линий электропередачи напряжением до 500 кВ включительно выбор сечения проводов производится по нормированным обобщенным показателям... Расчет питающей электрической сети 5.2 Определение параметров схемы замещения линии электропередачиДля определения параметров линии электропередачи составляется П-образная схема замещения: Рис.6. П-образная схема замещения линии электропередачи. В зависимости от класса напряжения среднегеометрическое расстояние можно принять по табл... Расчет питающей электрической сети 5. Определение сечений и выбор типа проводников линии электропередачиПри проектировании воздушных линий электропередачи напряжением до 500 кВ включительно выбор сечения проводов производится по нормированным обобщенным показателям... Расчет питающей электрической сети 5.2 Определение параметров схемы замещения линии электропередачиДля определения параметров линии электропередачи составляется П-образная схема замещения: Рис.6. П-образная схема замещения линии электропередачи. В зависимости от класса напряжения среднегеометрическое расстояние можно принять по табл... Расчет питающей электрической сети 5. Определение сечений и выбор проводников линии электропередачиСечение проводника считаем одинаковым на всех участках, в этом случае необходимо определить токи для участков с одинаковым направлением мощности. Ток протекающий по участку ЛЭП определяется по формуле А Где SНБ... Электрические сети предприятий железнодорожного транспорта 4. Определение потерь активной мощности и энергии в местной сетиПотери активной мощности в линии, определяемые по формуле (5.1)[2], рассчитываются при выборе кабелей по допустимой потере напряжения в п.2.: где Рi - активная мощность, протекающая в линии, кВт; Qi - реактивная мощность, протекающая в линии... Электроснабжение населенного пункта 10. Определение потерь мощности и энергии в сети высокого напряжения и трансформатореПравильный выбор электрооборудования, определение рациональных режимов его работы... Электроснабжение населенного пункта 12.определение сечения проводов и фактических потерь напряжения, мощности и энергии в сетях 0,38 квСечения проводов вл-0,38 кв определяются по экономическим интервалам, или по допустимой потере напряжения по формулам, соответствующим конфигурации сети. Сечения проводов магистрали по допустимой потере напряжения определяются по формуле... Электроснабжение сельского населенного пункта 12. Определение потерь мощности и энергии в сети высокого напряжения и трансформатореПравильный выбор электрооборудования, определение рациональных режимов его работы... Электроснабжение сельского населенного пункта 14. Определение сечения проводов и фактических потерь напряжения, мощности и энергии в сетях 0,38 кВСечения проводов ВЛ-0,38 кВ определяются по экономическим интервалам, или по допустимой потере напряжения по формулам, соответствующим конфигурации сети... fis.bobrodobro.ru Потери электроэнергии в воздушных ЛЭП: причины и методы борьбы | Новости
Часть этих проблем обусловлена спецификой работы воздушных ЛЭП, часть – с нарушением правил и норм прокладки и эксплуатации электросети. Так или иначе, во многих случаях бороться с этими проблемами приходится самим потребителям. Поэтому мы решили рассказать о причинах, а в следующей части статьи - и о доступных методах борьбы с подобными проблемами. Причины потерь: Увеличенное сопротивление линии Закон Ома показывает, что падение напряжения в электросети напрямую связано с увеличением сопротивления. Поэтому при пониженном напряжении на протяжении длительного периода времени необходимо снижать сопротивление ЛЭП. Оно складывается из сопротивления фазного провода и нуля от подстанции до непосредственно потребителя. Проблемы с реактивной нагрузкой Еще одной возможной причиной потерь является реактивная нагрузка. Если нагрузка только активная, например, источники освещения, обогреватель, электроплита, то энергию подобные приборы потребляют почти всю (кпд составляет > 90%). Однако гораздо чаще имеет место неполное потребление электроэнергии, образование паразитных токов в электропроводке. То есть, нагрузка является реактивной. В этом случае возникают дополнительные потери тока из-за нагрева, скачков напряжения и тока. По данным статистики, из-за некомпенсированной реактивной нагрузки бытовой потребитель теряет в среднем до 30% энергии. Для борьбы с этими потерями используются компенсаторы реактивной мощности, которые в большом количестве представлены сейчас на рынке электроприборов. Воровство Следующим источником потерь энергии является самое простое воровство. Конечно, этим должны заниматься и занимаются соответствующие государственные органы, но проводить энергоаудит они могут далеко не всегда. Поэтому и здесь решать проблему приходиться самим потребителям Метод оценки потерь на примере Активное сопротивление ЛЭП можно вычислить по формуле R=(L*p)/ S, где L – длина провода, p – его удельное сопротивление, а S – поперечное сечение. Удельное сопротивление меди и алюминия - 0,017 и 0,028 Ом*кв.мм/м соответственно. Как видно, p алюминия гораздо выше, однако алюминий также легче и дешевле меди, поэтому для строительства воздушных ЛЭП как правило используют именно алюминиевые провода, например, неизолированные провода СИП. . Предположим, что мы имеем дело с алюминиевым проводом, поперечное сечение которого составляет 20 мм2. Удельное сопротивление такого провода будет (0.028 х 1)/24=0.0014 Ом. Рассчитаем теперь потери в линии длиной 600 метров, с нагрузкой 4 кВт. Так как в линии проложены два провода, то расчетную длину линии увеличиваем вдвое – 1200 метров. Сила тока при нашей мощности составит 4000/220=18,2 А. Падение напряжения составит U=1200х0.0014х18.2=31 В. Напряжение на нагрузке 220-31=189 В. www.yugtelekabel.ru 5. ПОТЕРИ МОЩНОСТИ И ЭНЕРГИИ В ЭЛЕКТРИЧЕСКИХ СЕТЯХРежимные трудности усугубляются тем, что в настоящее время структура генерирующих мощностей меняется в сторону снижения маневренности, это связано с вводом в эксплуатацию крупных блоков. Для покрытия пиков нагрузки энергосистем приходится привлекать к переменным режимам работы блоки мощностью 200—300МВт на газомазуте, которые на это не рассчитаны. В отдельные дни электростанция мощностьюуст = 18 ГВт выдает до1,2—1,5ГВт. Около 50 % времени в году блоки эксплуатируются при нагрузках 40 % от номинальной мощности. При такой эксплуатации оборудования блоков снижается их экономичность. Снижение нагрузки энергосистем в воскресные дни приводит к необходимости отключения части блоков (20—25раз в году), что в свою очередь повышает аварийность оборудования, так как велика вероятность отказа блока при пуске (до 0,4). Исследования показали, что проблема покрытия графика нагрузки энергосистемы может быть решена только комплексно ––путем увеличения маневренности оборудования; сооружения пиковых электростанций; внедрения специальных блоков повышенной маневренности на газомазуте мощностью 500 МВт, использования газотурбинных станций; сооружения гидроаккумулирующих электростанций, введения режимных мероприятий, объединения энергосистем в единую ЭЭС РФ. Контрольные вопросы1.Каковы способы представления нагрузки как динамической характеристики? 2.Что такое типовые графики нагрузки? Какие графики используются в качестве типовых? 3.Каковы основные показатели графиков нагрузки? Разъяснить их смысл. 4.Как строится график нагрузки по продолжительности? 5.Назовите характерные показатели графиков нагрузок. 6.Как определяются показатели нагрузки узла сети по данным отдельных потребителей? 7.Как определяются показатели нагрузки системы по данным нагрузок подсистем? 8.Какие характерные зоны выделяют в графиках нагрузки? Передача электроэнергии сопровождается потерями активной и реактивной мощности и энергии. Потерянная энергия расходуется на нагрев проводов ЛЭП, обмоток, корпуса и сердечников трансформаторов. Потери активной мощности связаны с необходимостью установки дополнительной мощности генераторов и дополнительными расходами топлива, следовательно, дополнительными затратами на компенсацию потерь. Потери активной мощности в электрических сетях составляют от 2 до 6 % мощности нагрузок. Потери реактивной мощности в элементах электрических сетей приводят к возрастанию потерь активной мощности, обусловливают установку дополнительных компенсирующих устройств, что также связано с дополнительными затратами. Потери реактивной мощности в электрических системах в несколько раз больше потерь активной мощности, это объясняется соотношением актив-
Величина потерь реактивной мощности в элементах электрических систем составляет от 6 до 12 % мощности нагрузок [5]. Уровень потерь как активной, так и реактивной мощности зависит от класса напряжения сети и уменьшается с увеличением класса напряжения [1, 3, 4]. 5.1. Потери мощности в участке сетиРассмотрим участок сети, схема замещения которого показана на рис. 5.1. Обозначения, принятые на рисунке, следующее: — сопротивление, — проводимости схемы замещения, которые считаем заданными;
Здесь н ик ––соответственно потоки мощности в начале и конце сопротивления .
где ∆ ш , = 1, 2 — потери мощности в шунтах схемы замещения. Потери мощности в шунтах (5.2) не зависят от токов (потоков), передаваемых через участок сети, поэтому называются постоянными потерями. На основании первого закона Кирхгофа для узлов 1 и 2 можно записать
переменных потерь мощности может быть представлено в различных формах, например к к н н ∆ ; ∆. Следует обратить внимание, что потери мощности могут быть определены по данным как начала, так и конца участка — важно использовать напряжения и потоки мощности для одной и той же точки участка («к» или «н»). Для связи потоков и потерь можно использовать следующие выражения:
Активные потери в шунтах ∆ ш определяются потерями на корону, а реактивная составляющая∆ ш определяется емкостной генерацией линии. Обычно для расчетов потери активной мощности на корону в ЛЭП принимают равными средним удельным потерям∆ кор.ср и определяют из справочников [5, табл.
Переменную составляющую потерь мощности можно определить по введенным ранее формулам (5.5). Вприближенных расчетах, когда неизвестны точные значения напряжений вузлах электрической сети, потери мощности можно определять по прибли- женным (средним) значениям напряжений . 5.3. Потери мощности в трансформаторахСхема замещения двухобмоточного трансформатора отличается от схемы замещения рис. 5.1 только тем, что = 0, поэтому введенные ранее выражения для вычисления потерь также справедливы для трансформаторов. 37 Для приближенных расчетов постоянную составляющую потерь в транс-
трансформаторах (потери в меди) в соответствии с (5.4) может быть определена по формуле
При определении потерь мощности в трехобмоточных трансформаторах и автотрансформаторах следует учитывать загрузку каждой из обмоток трансформаторов и потери короткого замыкания каждой из обмоток:
где — число трансформаторов;в,с,н — потоки мощности по обмоткам высшего, среднего и низшего напряжения соответственно;∆ кв.з,∆ кс.з,∆ кн.з — потери короткого замыкания обмоток;ном — номинальная мощность трансформатора. 5.4. Потери энергии в элементах электрических сетейВеличина потерь электроэнергии зависит от потерь мощности и времени работы сети. Рассмотрим передачу мощности через трансформатор (рис. 5.2). 38
бителей не остаются постоянными, а меняются в соответствии с графиком нагрузки (рис. 5.3, а). Тогда переменная составляющая потерь активной мощно-
studfiles.net | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|




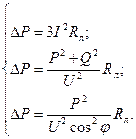
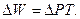
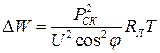 .
.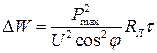 .
.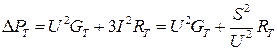 .
.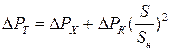 .
.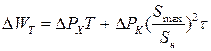 .
.
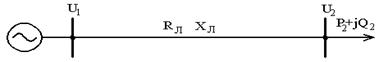
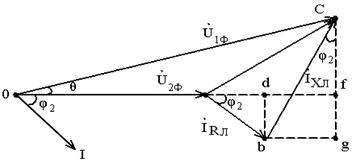
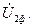 На угол φ2от него отстает ток нагрузки. Вектор IRЛпредставляет собой напряжение собой на RЛ ,он отложен параллельно току
На угол φ2от него отстает ток нагрузки. Вектор IRЛпредставляет собой напряжение собой на RЛ ,он отложен параллельно току 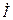 . Вектор
. Вектор 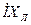 . – напряжение на индуктивном сопротивлении линии, он опережает вектор тока на 900. Сумма этих двух векторов (вектор
. – напряжение на индуктивном сопротивлении линии, он опережает вектор тока на 900. Сумма этих двух векторов (вектор 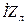 ) называется падением напряжения в линии.Сумма векторов
) называется падением напряжения в линии.Сумма векторов 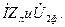 дает вектор напряжения в начале линии
дает вектор напряжения в начале линии 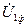 . Падением напряжения в линии называется векторная разность напряжений в начале и в конце линии:
. Падением напряжения в линии называется векторная разность напряжений в начале и в конце линии: 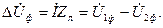
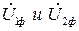 :
: 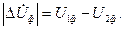
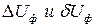 соответственно, они определяются:
соответственно, они определяются: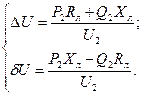
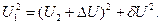
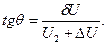
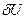 ,и при этом считается, что продольная составляющая падения напряжения равна потере напряжения.
,и при этом считается, что продольная составляющая падения напряжения равна потере напряжения.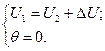
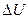 приближенно определяется без учета потерь мощности (мощности в начале и в конце одинаковы) при номинальном напряжении электропередачи.
приближенно определяется без учета потерь мощности (мощности в начале и в конце одинаковы) при номинальном напряжении электропередачи.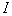 или его активной
или его активной 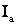 и реактивной
и реактивной 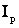 составляющих, потери активной мощности , расходуемые в активном сопротивлении
составляющих, потери активной мощности , расходуемые в активном сопротивлении 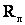 линии на нагрев проводников, определяют по формулам
линии на нагрев проводников, определяют по формулам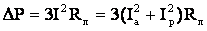 . (5.1)
. (5.1)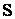 , активной
, активной 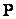 и реактивной
и реактивной 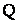 мощности, то те же потери можно найти по выражениям
мощности, то те же потери можно найти по выражениям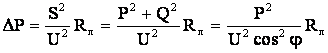 . (5.2)
. (5.2)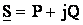 . Потери активной мощности в ней
. Потери активной мощности в ней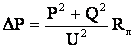 .
.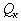 . При этом передаваемая по линии реактивная мощность снизится до величины
. При этом передаваемая по линии реактивная мощность снизится до величины 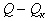 , а значит уменьшатся и потери активной мощности
, а значит уменьшатся и потери активной мощности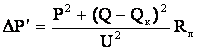 .
.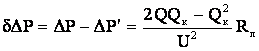 (5.3)
(5.3)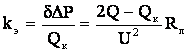 (5.4)
(5.4)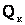 .
.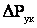 во многом зависит от погодных условий и от напряжения.
во многом зависит от погодных условий и от напряжения.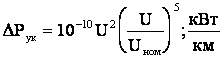 , (5.5)
, (5.5)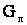
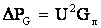 . (5.6)
. (5.6)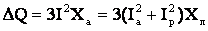 .
. 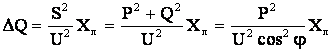 . (5.7)
. (5.7)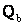 , является источником реактивной мощности. Зарядная мощность линии, определяемая формулой (4.14), в некоторых случаях снижает реактивную мощность, передаваемую по линии, а значит и потери активной и реактивной мощности. Вместе с тем, в режимах наименьших нагрузок, когда имеет место избыток реактивной мощности, зарядная мощность может вызвать увеличение передаваемой по линии реактивной мощности и потерь мощности.
, является источником реактивной мощности. Зарядная мощность линии, определяемая формулой (4.14), в некоторых случаях снижает реактивную мощность, передаваемую по линии, а значит и потери активной и реактивной мощности. Вместе с тем, в режимах наименьших нагрузок, когда имеет место избыток реактивной мощности, зарядная мощность может вызвать увеличение передаваемой по линии реактивной мощности и потерь мощности. Практически каждый, кто живет в частном доме, на даче или в деревне время от времени сталкивается с проблемой защиты и эксплуатации электроприборов в условиях сильных скачков напряжения в электросети.
Практически каждый, кто живет в частном доме, на даче или в деревне время от времени сталкивается с проблемой защиты и эксплуатации электроприборов в условиях сильных скачков напряжения в электросети.