Схемы резервирования инженерных систем ЦОДЧто такое схема с N элементами в системе резервирования и как разобраться с, казалось бы, сложной таблицей Менделеева дата-центра?
Прежде всего, необходимо сказать, что обозначение N происходит от английского слова «need», что в переводе обозначает «необходимость». А для ЦОД необходима его бесперебойная работа, то есть системы резервирования прежде всего отвечают за отказоустойчивость источников бесперебойного питания и систем охлаждения.
Для системы резервирования этот символ N является обозначением необходимой нагрузки для эффективной работы оборудования. В одной системе, как правило, используются несколько N элементов. Их принцип работы зависит от схем, по которым они были воспроизведены. Существует несколько основных видов резервирования: N, N+1, 2N, 2N+1, 2(N+1), 3/2N.
В зависимости от установленной схемы резервирования можно говорить об отказоустойчивости системы: чем система сложнее, тем она дороже и, соответственно, более устойчива к отказам и ошибкам.
N. Отличительная черта такой схемы резервирования в том, что как такового резервирования в ней нет, а надежность зависит от каждого отдельного элемента N. При сбое в работе одного из них незамедлительно будет прекращена вся работа системы. Причина в том, что, когда один из элементов выходит из строя, его нагрузку перераспределить будет некуда. В результате такого сбоя данные могут быть безвозвратно утеряны, и это повлечет за собой, соответственно, материальные убытки. Эта схема уже давно не эксплуатируется как раз по причине того, что цена простоя всего ЦОД в случае неполадок слишком высока. По сути, при данной схеме зачастую отсутствует сам ИБП или генератор, а если даже они и есть, то представлены одномодульными системами.
N+1 – схема с одним резервным элементом N. В системе N+1 резервный элемент остается незадействованным в работе до тех пор, пока в системе не произойдет сбой одного из основных элементов.
Для этого предусмотрены вариации: N+2, N+3 и т.д., в зависимости от требований уровня надежности и безопасности. Но стоит учитывать, что в этом варианте усложнение схемы может привести к большему простою.
2N – это две полные параллельные системы для каждого элемента N. То есть каждый элемент N в такой схеме дублируется, а нагрузка одинакова на двух элементах. При этом ни один из них никогда не нагружается полностью, и системы делят нагрузку 50/50, но эффективность работы при этом значительно снижается. Однако, при такой системе резервирования сбой одного или нескольких элементов N или выход из строя одной из систем не повлияют на работу всей системы в целом.
2N+1 — это параллельная система резервирования, схожая с системой 2N, но с одним дополнительным резервным элементом.
Таким образом, если ЦОД выйдет из строя или потребуется техническое обслуживание, то всю нагрузку можно перенести на параллельный блок, в то время как сам дата-центр продолжит работу без остановок.
Схема 2(N+1) – это параллельная система резервирования с дополнительным элементом N, в которой резервный элемент дублируется, то есть это две полные системы по схеме N+1. При возникновении сбоя или необходимости технического обслуживания резервные элементы N остаются в любом случае, резервируются и ИБП, и системы охлаждения, ДГУ ждет своего часа на отдельной площадке. Эта система считается самой отказоустойчивой.
Схема 3/2N включает в себя все преимущества системы 2N, но такая система загружена на 2/3, а не на 50/50 как в системе 2N, соответственно и производительность у 3/2N будет намного выше, а счета за электричество – значительно меньше.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В случае возникновения такого сбоя, резервный элемент примет на себя всю его нагрузку. Таким образом, система продолжит работать, но необходимость отключать всю систему для проведения ремонтных работ все еще возникнет.
При отказе одного из элементов минимальна вероятность потери нагрузки. Даже если выйдет из строя один из ИБП, то его нагрузку подхватит соседняя система. Как и в любой другой схеме, здесь возможны вариации: к примеру, если добавить четвертую группу ИБП, то схема уже будет называться 4/3 N. Как ни странно, данная схема пришла их сетей передачи данных и большой популярности у дата-центров не пользуется.
23%
5сек
90%
000001сек
58%
9·10-18%
67секПоддерживаемые форматы обозначений—ArcGIS Pro | Документация
В ArcGIS Desktop поддерживается ряд форматов чтения и записи местоположений координат из текстовой строки.
Координаты с форматированным обозначением можно использовать в инструментах геообработки, например в инструменте Конвертировать обозначения координат.
В примерах и пояснениях ниже используется следующий синтаксис:
- | означает «или». Например, + | — означает, что можно использовать либо символ + либо -.
- [ ] обозначает список выбора. Например, [ + | — | N | S] означает, что можно использовать символы +, -, N либо S.
- < > обозначает значение.
Локализация для десятичных символов или аббревиатур полушария. Например, для выражения десятичных значений можно использовать только точку, но не запятую. Для обозначения полушарий используются только символы N, S, E и W, но не соответствующим им буквы других языков.
Форматы, использующие градусы
Для форматов, использующие градусы, первым всегда указывается значение широты (координата Y), затем значение долготы (координата X).
Задайте полушарие с помощью обозначений +,-,N,S,E или W. Их можно смешивать в одной паре координат широта-долгота. Если они не указаны, значение считается положительным (N для широты или E для долготы).
DD (десятичные градусы)
Входной формат
<широта> <разделитель_пары_координат> <долгота>
|
широта |
[ + | — | N | S ] <DD.dd> [ + | — | N | S ] |
Регистр не учитывается |
|
долгота |
[ + | — | E | W ] <DDD.dd> [ + | — | E | W ] |
Регистр не учитывается |
|
разделитель_пары_координат |
[space | / | \ | | | , ] |
Может использоваться несколько разделителей, например, запятая и пробел, два пробела |
Значения <DD.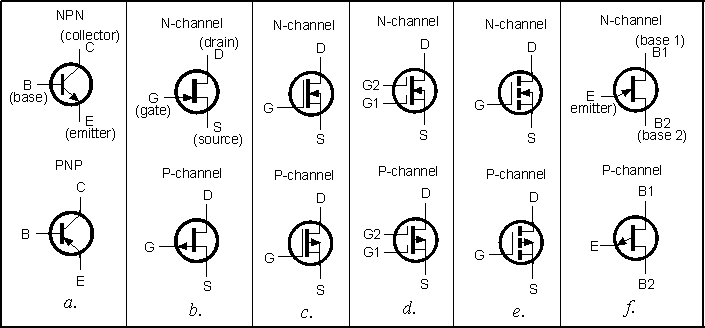
(U+005E)
Тильда ~ (U007e)
Звездочка * (U+002A)
Знак градуса может не указываться.
Общая длина значения не может превышать 64 символа (включая конечный символ NULL).
Примеры ввода
Все следующие примеры ввода являются равноценными:
27.00N 087.00W27.00n 087.00w27.00N 087W+27.00 087W27N -87N27.00 W08727.00N/87W27.00N/87W27.00°N 087.00°W
Выходной формат
При записи обозначения десятичного градуса добавляются начальные нули и используются буквы для обозначения полушария.
Пример результата
Этот выходной формат используется ArcGIS по умолчанию.
27.00N 087.00W 27.00000N 087.00000W
DDM (градусы — минуты)
Нельзя указывать несколько знаков +/- signs в формате DD MM.mmm.
Входной формат
<широта> <разделитель_пары_координат> <долгота>
|
широта |
[ + | — | N | S ] <DD MM. |
Регистр не учитывается |
|
долгота |
[ + | — | E | W ] <DDD MM.mmm> [ + | — | E | W ] |
Регистр не учитывается |
|
разделитель_пары_координат |
[space | / | \ | | | , ] |
Может использоваться несколько разделителей, например, запятая и пробел, два пробела |
mmm> [ + | — | N | S ] Значения широты <DDD MM.mmm> и долготы <DD MM.mmm> могут указываться в следующем формате:
<градусы> [<знак_градуса>] [<разделитель>] <минуты> [<десятичный знак>] <доля минуты> [<знак_минуты>]
|
градусы |
0 – 90 (широта) От 0 до +180 и от 0 до -180 (долгота) |
|
знак_градуса |
Знак градуса ° (U+00B0) Кольцо над ° (U+02DA) Порядковый указатель в муж. Тильда ~ (U007e) Звездочка * (U+002A) |
|
разделитель |
[ пробел | нижнее подчеркивание | дефис] |
|
минуты |
от 0 до 59 |
|
десятичное |
. |
|
доля минуты |
знаки |
|
знак_минуты |
Знак минуты ‘ (U+2032) Апостроф ‘ (U+0027) |
(U+005E)Знаки градуса и минуты могут не указываться.
Общая длина строкового значения не может превышать 64 символа (включая конечный символ NULL).
Примеры ввода
Все следующие примеры ввода являются равноценными:
27 54.00N 087 59.00W27 54.00n 087 59.00w27 54N 087 0W+27 54.00 087 59.00WN27 54.00 W087 59.0027 54.00N/87 59W27° 54.00’N 087° 59.00’W
Пример результата
Этот стандартный выходной формат используется ArcGIS по умолчанию.
27.00N 087.00W27 00.00000N 087 00.00000W
DMS (градусы-минуты-секунды)
Нельзя указывать несколько знаков +/- signs в формате DD MM SS.sss.
Входной формат
<широта> <разделитель_пары_координат> <долгота>
|
широта |
[ + | — | N | S ] <DD MM SS.sss> [ + | — | N | S ] |
Регистр не учитывается |
|
долгота |
[ + | — | E | W ] <DDD MM SS. |
Регистр не учитывается |
|
разделитель_пары_координат |
[space | / | \ | | | , ] |
Может использоваться несколько разделителей, например, запятая и пробел, два пробела |
sss> [ + | — | E | W ]Значения широты <DDD MM SS.sss> и долготы <DD MM SS.sss> могут указываться в следующем виде:
<градусы> [<знак_градуса>] <разделитель> <минуты> [<знак_минуты>] <разделитель> <секунды> [<десятичный знак>] <доля секунды> [<знак_секунды>]
|
градусы |
0 – 90 (широта) От 0 до +180 и от 0 до -180 (долгота) |
|
знак_градуса |
Знак градуса ° (U+00B0) Кольцо над ° (U+02DA) Порядковый указатель в муж. Тильда ~ (U007e) Звездочка * (U+002A) |
|
разделитель |
[ пробел | нижнее подчеркивание | дефис] |
|
минуты |
от 0 до 59 |
|
знак_минуты |
Знак минуты ‘ (U+2032) Апостроф ‘ (U+0027) |
|
секунды |
от 0 до 59 |
|
десятичное |
«.» |
|
доля секунды |
знаки |
|
знак_секунды |
Кавычка » (U+0022) Трема ¨ (U+00A8) Двойной акут ˝ (U+02DD) |
(U+005E)Знаки градуса, минуты и секунды могут не указываться.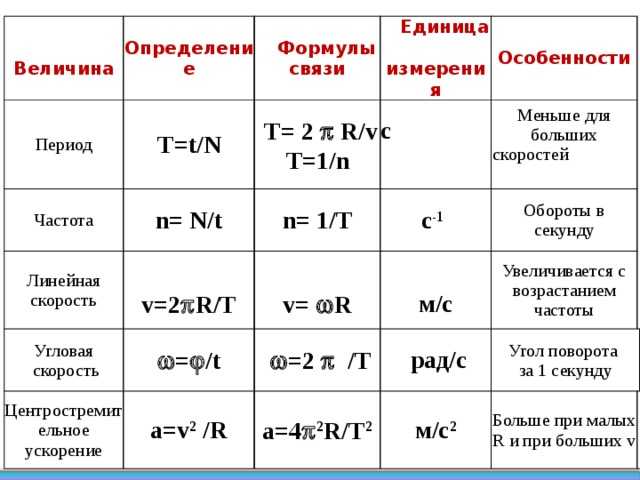
Общая длина строкового значения не может превышать 64 символа (включая конечный символ NULL).
Примеры ввода
Все следующие примеры ввода являются равноценными:
27 18 00.00N 087 00 00.00W271800.00N 0870000.00W
Также поддерживается компактный формат DDMMSS.sss.
Пример результата
Этот стандартный выходной формат используется ArcGIS по умолчанию.
27 18 00.00N 087 00 00.00W
Универсальная поперечная проекция Меркатора (UTM)
При использовании обозначений UTM указывается зона и буква. Буква обычно представляет канал широты как в MGRS/USNG. В отдельных случаях могут использоваться буквы N или S для обозначения зоны UTM «Север» или «Юг». В смешанном списке всегда считается, что обозначения UTM использует канал широты.
Если обозначение UTM представлено строкой, не содержащей пробелов, часть строки, относящаяся к сдвигу на восток и на север разбивается на две половины. Если указано нечетное количество символов, лишний символ относится к части сдвига на север.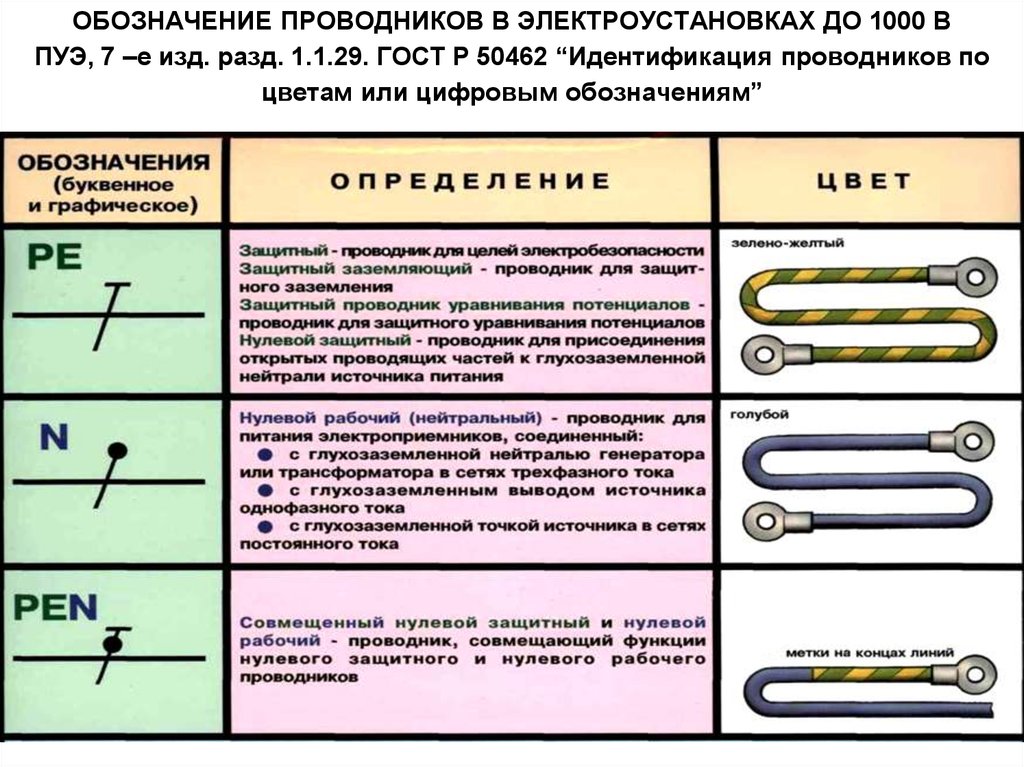
Значения сдвига на восток и на север должны быть целыми числами.
11S3455674321459 = 11S 345567 4321459
11N345567432145 = 11N 345567 432145
Внимание:
Если обозначение UTM не содержит встроенных пробелов, четное количество символов может привести к противоречию. Например, сдвиг на восток должен содержать пять знаков, а сдвиг на север — семь, однако, программное обеспечение интерпретирует оба эти значения как содержащие шесть символов.
Если значение содержит встроенные пробелы, значения сдвига на восток и на север предположительно будут разделены пробелом и могут дополнительно содержать десятичные точки
Этот формат не поддерживается:
11S 3455674321459
при наличии запятой должен использовать строковый формат Easting,Northing,ZoneBand.
554577,4183342,10S
Допускается использование десятичных запятых. Пробелы в формате такого типа игнорируются.
554577.3,4183342.7,10S
Примеры ввода
Все следующие примеры ввода являются равноценными:
11S 345567 432145911S3455674321459554577,4183342,10S554577.3,4183342.7,10S554577, 4183342, 10S
3,4183342.7,10S554577, 4183342, 10SПример результата
11T 561192 4832027
Военная система прямоугольных координат (MGRS)
ZZBGGEEEEENNNNN
- ZZ: зона UTM
- B: канал широты
- GG: буквы, обозначающие площадь сетки 100 K (универсальная полярная стереографическая проекция для полярных регионов)
- EEEEE: координата X (сдвиг на восток)
- NNNNN: координата Y (сдвиг на север)
Сочетание первых трех букв ZZB иногда называют «Обозначение фрагмента сетки».
Использование пробелов допускается во входных данных, но не между значениями сдвига на восток и на север. После значений сдвига на восток указываются значения сдвига на север. Количество знаков, используемых для значений сдвига на восток и сдвига на север, должно совпадать.
Координаты MGRS можно округлить для меньшей точности. Пример:
- 15SWC8081751205 указывается с точностью до 1 метра.
- 15SWC80825121 указывается с точностью до 10 метров.
- 15SWC808512 указывается с точностью до 100 метров.
- 15SWC8151 указывается с точностью до 1000 метров.
В зависимости от датума или эллипсоида для MGRS будет использован новый или старый стиль. Старый стиль использует альтернативную схему присвоения букв. USNG (упрощенная версия MGRS) использует только новый формат, даже если он основывается на датуме NAD 1927, при использовании которого в MGRS применяется старый стиль. В целом одна из схем используется для WGS 1984 и NAD 1983, а вторая – для более ранних эллипсоидов, связанная с локальными датумами. Например, эта координата указана в формате WGS 1984:
15SWC8081751205
При ее преобразовании в схему датума NAD-27 datum, эллипсоид Clarke 1866, присваивается следующее значение:
15SWN8083350993
Универсальная полярная стереографическая проекция (UPS) разделает антарктический регион на зоны A и B, а арктический регион — на зоны Y и Z.
Номера зонам не присваиваются.
ZAK4500045522 = 169 36 50.2E 87 45 7.2N = (169.6139E 87.7520N)
ZGG7902863771 = 85:40:30.0 N 85:40:30.0 W
ATN2097136228 = 85:40:30.0 S 85:40:30.0 W
Примеры ввода
Все следующие примеры ввода являются равноценными:
15SWC808175120515S WC 8081751205ZAK4500045522
Пример результата
По стандарту использование пробелов в выходных данных не допускается.
15SWC8081751205ZAK4500045522
United States National Grid (USNG)
Схема обозначения координат в системе USNG представляет собой упрощенную версию MGRS на основе национальной энергосистемы США.
Дополнительные сведения см. в разделе Стандарт United States National Grid, FGDC-STD-011-2001.
USNG поддерживает только две географические системы координат: NAD 1983 (эквивалентна WGS 1984) и NAD 1927. USNG по умолчанию использует NAD 1983.
При использовании системы NAD27 необходимо явно задать ее, например: 18SUJ2306 (NAD 27). В отличие от MGRS, USNG использует ту же схему присвоения букв для своих 100 км квадратов независимо от используемой системы географических координат. MGRS сдвигает северную букву на 10 знаков при использовании старого стиля с NAD 1927. Таким образом, MGRS и USNG, основанные на NAD 1927, нельзя включить в смешанный список обозначений.
В отличие от MGRS в USNG допускается использование пробелов, например 18T WL 807 046.
Система USNG применяется только для территории США, включая внешние владения и территории. Координаты MGRS определяются для всей карты мира – в диапазоне значений широты между 80°S и 84°N определение выполняется средствами UTM, однако, вне этого диапазона координаты определяются в рамках универсальной полярной стереографической проекции (UPS). Из-за ограничений диапазона USNG не требует использования UPS и определяется исключительно средствами UTM.
Примеры ввода
Все следующие примеры ввода являются равноценными:
11SMT824647520711S MT 82464 75207
Пример результата
11S MT 82464 75207
Всемирная система географических координат (GEOREF)
Система GEOREF основана на координатах долготы и широты.
Карта мира разделяется сначала на ячейки 15х15 градусов, которые помечены буквами. Каждая из этих ячеек затем подразделяется на ячейки 1х1 градус, также с буквенным обозначением. Каждая из ячеек 1х1 градус может быть разделена на ячейки 60х60 минут, как показано в примере ниже. Дальнейшие деления допускаются до 0,01 минуты.
Пример ввода
PGAM16281221
Пример результата
PGAM1628
Global Area Reference System (GARS)
Система GARS основана на координатах широты и долготы. Карты мира подразделяется на ячейки 30х30 минут. Первые три символа представляют полосу долготы шириной 30 минут. Четвертый и пятый символы представляют полосу долготы высотой 30 минут. Каждую из ячеек 30х30 минут можно разделить на четыре ячейки 15х15 минут, и каждую из них – на девять ячеек 5х5 минут. При преобразовании из GARS нижний левый угол представленного квадрата используется для вычисления координат в градусах.
Примеры ввода
391JL41391JL
Пример результата
391JL41
Смешанные форматы обозначений
В отношении преобразования набора смешанных строковых обозначений действуют следующие условия.
Эффективное определение некоторых форматов обозначения невозможно.
Все списки смешанных форматов обозначений должны использовать одинаковую систему географических координат (датум). Система GCS не задана явно, WGS 1984 подразумевается.
В зависимости от датума или эллипсоида для MGRS будет использован новый или старый стиль. Старый стиль использует альтернативную схему присвоения букв. USNG (упрощенная версия MGRS) использует только новый формат, даже если он основывается на датуме NAD 1927, при использовании которого в MGRS применяется старый стиль. Если строковые обозначения и MGRS, и USNG, использующие систему NAD 1927, находятся в одном списке, корректное преобразование в другой тип координат или обозначений невозможно.
При использовании обозначений UTM указывается зона и буква. Буква обычно представляет канал широты как в MGRS/USNG. В отдельных случаях могут использоваться буквы N или S для обозначения зоны UTM «Север» или «Юг». В смешанном списке всегда считается, что обозначения UTM использует канал широты.
Координаты GARS должны располагаться слева внизу (не в центре).
Формат DD.MMSSsss не поддерживается (возможно противоречие с DD.dddddd или DD.MMmmm).
При указании всех обозначений в градусах (например, DD.dddd, DDMM.mmmm, DDMMSS.ssss или DD MM SS.ssss) значения широты и долготы должны указываться в одинаковом формат.
Можно комбинировать +/- или NSEW, но эти обозначения следует указывать в начале или конце значения (dd mm ss.ssss-).
Нельзя указывать несколько знаков +/- signs в формате DD MM.mmm или DD MM SS.ssss.
Отзыв по этому разделу?
N-обозначение | Хайброу
03.07.2018
|
0
Эпизод №2 курса Курта Андерсона по основам информатики
С возвращением!
Вчера мы рассмотрели основы работы самих компьютеров. Сегодня мы познакомимся со строительными блоками алгоритмического анализа — основной концепции компьютерных наук.
Что такое N-нотация?
N-нотация — это способ представления времени выполнения алгоритма, чтобы его можно было сравнить с другим алгоритмом.
N-нотация — это НЕ анализ того, сколько времени потребуется для запуска алгоритма, а анализ того, как алгоритм будет масштабироваться с увеличением количества входных данных.
Этот метод основан на просмотре входных данных алгоритма и анализе того, как алгоритм работает с этими входными данными. Однако мы точно не знаем, сколько фрагментов данных будет поступать в любой момент. Что мы делаем, так это заменяем этот входной номер переменной n .
Допустим, у нас есть алгоритм, который проверяет количество ваших друзей на Facebook. Когда мы пишем алгоритм, мы понятия не имеем, сколько друзей будет добавлено в качестве входных данных. Вы могли бы иметь 25 или 2000 или два. Итак, вместо того, чтобы указывать фактическое число, мы просто говорим 9.0023 n элемента данных будут помещены в этот алгоритм.
Как использовать N-нотацию
Как мы используем это для сравнения двух алгоритмов? Что мы делаем, так это ищем существенные различия в алгоритмах.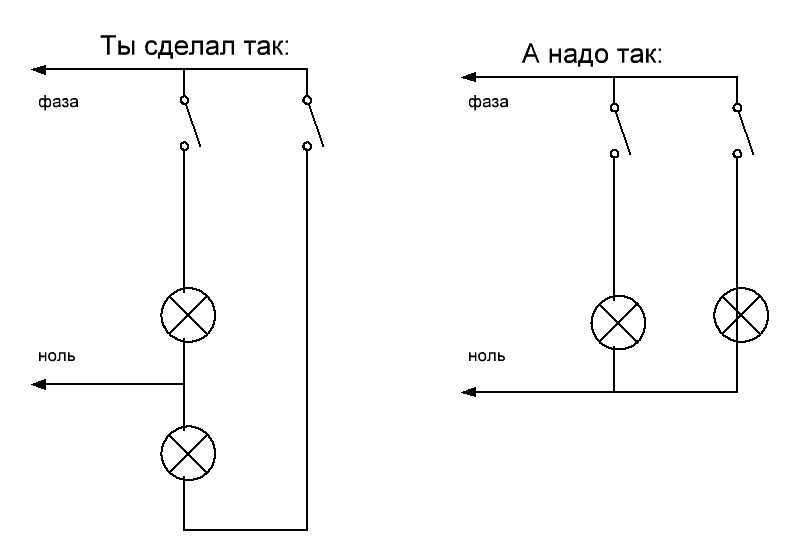
Как отреагирует программа на ввод n ?
© Cmglee
На приведенной выше диаграмме мы можем увидеть эти различные отношения в виде графика. Ось x (нижняя часть графика) показывает, сколько фрагментов данных поступает в алгоритм. Ось Y (слева) показывает, сколько операций программа должна будет выполнить с учетом количества частей данных.
Что же тогда показывает эта диаграмма? Он отображает отношения, о которых мы говорили. Центральная зеленая линия — n . Это означает, что если мы вставим n элементов данных, алгоритм выполнит n операций. Для ста единиц данных потребуется 100 операций, для 200 — 200 и так далее. Обратите внимание, что для некоторых других строк требуется значительно больше операций при том же объеме входных данных.
Реальным примером этого может быть копирование рукописной электронной таблицы в Excel. Вы, в данном случае, являетесь алгоритмом. Для каждой части данных в этой печатной копии вам нужно будет выполнить одну операцию, вставив ее в Excel.
2 (т. е. n*n).
Ключевым моментом здесь является признание сложности проблем по мере их масштабирования. Первая проблема довольно проста. У вас может быть 1000 или 100 000 страниц, и проблема не выйдет из-под контроля. Это могло наскучить, но ничего, что несколько часов не могли бы решить.
Однако представьте, что при сравнении проверяются полные 1000 страниц для каждого отдельного числа. А если у вас 10 000 или 100 000 страниц? Проблема быстро становится неуправляемой. Это то, что мы рассматриваем с помощью n-обозначения — отношение между вводом и ростом проблемы.
Вот сравнение того, как разные алгоритмы могут работать с реальными числами.
Основные выводы:
• N-нотация используется для сравнения роста алгоритмов, а не их фактического времени.
• N используется как переменная для того, сколько фрагментов данных вводит алгоритм. Затем мы смотрим на взаимосвязь с тем, сколько операций он должен выполнить при таком количестве входных данных.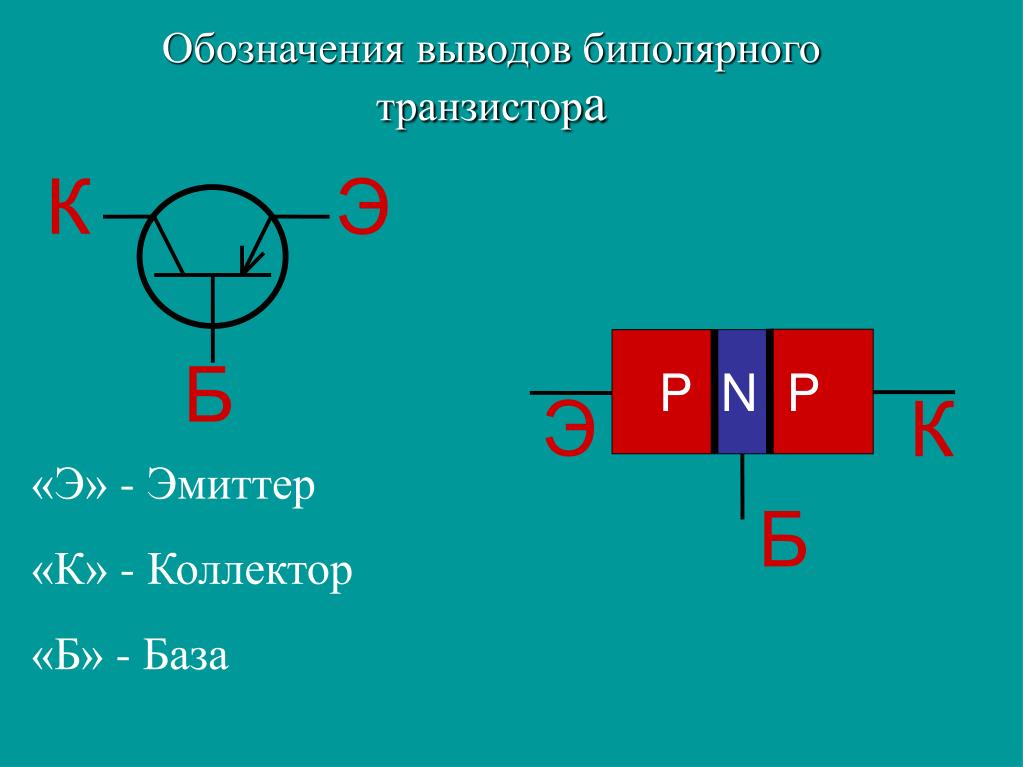
Завтра мы расширим эту идею с помощью нотации Big O.
Ура,
Kurt
Рекомендуемая книга
Элементы вычислительных систем: строительство современного компьютера с первых принципов от Noam Nisan, Shimon Schocken
. являются асимптотическими обозначениями в анализе сложности алгоритмов
Мы обсудили асимптотический анализ, а также наихудшие, средние и наилучшие случаи алгоритмов. Основная идея асимптотического анализа состоит в том, чтобы иметь меру эффективности алгоритмов, которая не зависит от машинно-специфических констант и не требует реализации алгоритмов и времени, затрачиваемого программами на сравнение. Асимптотические обозначения — это математические инструменты для представления временной сложности алгоритмов асимптотического анализа. Существует в основном три асимптотических обозначения: 1. Тета-нотация охватывает функцию сверху и снизу. Поскольку он представляет собой верхнюю и нижнюю границы времени работы алгоритма, он используется для анализа средний случай сложность алгоритма. Пусть g и f — функция от множества натуральных чисел к самой себе. Функция f называется Θ(g), если существуют константы c1, c2 > 0 и натуральное число n0 такие, что c1* g(n) ≤ f(n) ≤ c2 * g(n) для всех n ≥ n0 Тета-нотация Математическое представление тета-нотации:
Θ (g(n)) = {f(n): существуют положительные константы c1, c2 и n0 такие, что 0 ≤ c1 * g(n ) ≤ f(n) ≤ c2 * g(n) для всех n ≥ n0} Примечание: Θ(g) представляет собой набор Приведенное выше выражение можно описать так, как если бы f(n) есть тета g(n), тогда значение f(n) всегда находится между c1 * g( n) и c2 * g(n) для больших значений n (n ≥ n0). Простой способ получить тета-нотацию выражения состоит в том, чтобы отбросить члены младшего порядка и игнорировать начальные константы. Например , Рассмотрим выражение 92+log(n))} принадлежит Θ( n 2 ) Примечание: Θ обеспечивает точные границы. 2. Нотация Big-O (O-нотация) :
Нотация Big-O представляет верхнюю границу времени выполнения алгоритма. Следовательно, это дает наихудшую сложность алгоритма. Если f(n) описывает время работы алгоритма, f(n) равно O(g(n)) при условии, что существуют положительная константа C и n0 такие, что 0 ≤ f(n) ≤ cg(n ) для всех n ≥ n0
Тета-нотация (Θ-нотация) :
Определение тета также требует, чтобы f(n) было неотрицательным для значений n, превышающих n0.
Математическое представление записи Big-O:
O(g(n)) = { f(n): существуют положительные константы c и n0 такие, что 0 ≤ f(n) ≤ cg(n ) для всех n ≥ n0 }
Например, , Рассмотрим случай сортировки вставками.
В лучшем случае требуется линейное время, а в худшем — квадратичное время. Можно с уверенностью сказать, что временная сложность сортировки вставками составляет O(n 2 ).
Примечание : O(n) 2 ) также охватывает линейное время.
Если мы используем обозначение Θ для представления временной сложности сортировки вставками, мы должны использовать два утверждения для лучшего и худшего случаев:
Обозначение Big-O полезно, когда у нас есть только верхняя граница временной сложности алгоритма. Много раз мы легко находим верхнюю границу, просто взглянув на алгоритм. 92)
Примечание: Здесь U представляет объединение , мы можем записать его таким образом, потому что O обеспечивает точные или верхние границы.
3. Обозначение Омега (Обозначение Ω- ) :
Обозначение Омега представляет нижнюю границу времени выполнения алгоритма.
Таким образом, он обеспечивает наилучшую сложность алгоритма. Пусть g и f — функция от множества натуральных чисел к самой себе. Функция f называется Ω(g), если существуют константа c > 0 и натуральное число n0 такие, что c*g(n) ≤ f(n) для всех n ≥ n0
Математическое представление нотации Омега:
Ω(g(n)) = { f(n): существуют положительные константы c и n0 такие, что 0 ≤ cg(n) ≤ f(n) для все n ≥ n0 }
Рассмотрим тот же пример сортировки вставками. Временная сложность сортировки вставками может быть записана как Ω(n), но это не очень полезная информация о сортировке вставками, поскольку нас обычно интересует наихудший, а иногда и средний случай.
94 } принадлежит к Ω(1)
Примечание: Здесь U представляет объединение, мы можем записать его таким образом, потому что Ω обеспечивает точные или нижние границы.
Свойства асимптотических обозначений:
1.
Общие свойства:
O(g(n)) , где a — константа.
Пример:
f(n) = 2n²+5 равно O(n²)
тогда 7*f(n) = 7(2n²+5) = 14n²+35 также равно O(n²).Аналогично, это свойство удовлетворяет обозначениям как Θ, так и Ω.
Можно сказать,
Если f(n) равно Θ(g(n)) тогда a*f(n) также равно Θ(g(n)), где a — константа.
Если f(n) есть Ω (g(n)), то a*f(n) также есть Ω(g(n)), где a — константа.
2. Переходные свойства:
Если f(n) равно O(g(n)) и г(n) равно O(h(n)) , тогда f(n) = O(h(n)) .
Пример:
Если f(n) = n, g(n) = n² и h(n)=n³
n равно O(n²) и n² равно O(n³), то n равно O( n³)Аналогично, это свойство удовлетворяет как Θ, так и Ω-обозначению.
Можно сказать,
Если f(n) равно Θ(g(n)) и g(n) равно Θ(h(n)) тогда f(n) = Θ(h(n) ).
Если f(n) равно Ω (g(n)) и g(n) равно Ω (h(n)), то f(n) = Ω (h(n))
3. Рефлексивные свойства :
Рефлексивные свойства всегда легко понять после транзитивных.
Если f(n) задано, то f(n) равно O(f(n)). Поскольку МАКСИМАЛЬНОЕ ЗНАЧЕНИЕ f(n) будет САМ f(n)!
Следовательно, x = f(n) и y = O(f(n) всегда связаны рефлексивным отношением.
Пример:
f(n) = n² ; O(n²) т. е. O(f( n))
Аналогично, это свойство удовлетворяет как Θ, так и Ω.
Можно сказать, что0006
Если f(n) задано, то f(n) равно Θ(f(n)).
Если f(n) задано, то f(n) равно Ω (f(n)).
4. Свойства симметрии:
Если f(n) равно Θ(g(n)) , то g(n) равно Θ(f(n)) .
Пример:
Если(n) = n² и g(n) = n²
, то f(n) = Θ(n²) и g(n) = Θ(n²)Этому свойству удовлетворяет только для обозначения Θ.
5. Транспонированные симметричные свойства:
Если f(n) равно O(g(n)) , то g(n) равно Ом (f(n)) .
Пример:
Если (n) = n , g(n) = n²
, то n равно O(n²) и n² равно Ω (n)Это свойство удовлетворяет только обозначениям O и Ω.
6. Еще несколько свойств:
1. Если f(n) = O(g(n)) и f(n) = Ω(g(n)) , то f( n) = Θ(g(n))
2. Если f(n) = O(g(n)) и d(n)=O(e(n)) , затем f(n) + d(n) = O(max(g(n), e(n)))
Пример:
f(n) = n т.
Добавить комментарий