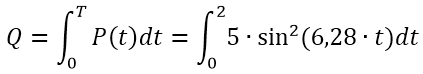Мощность в цепях переменного тока. Мощность переменного токаПеременный ток, мощность переменного токаВ свое время Эдисон и Тесла были противниками в вопросе использования электрического тока в энергетике. Тесла считал, что необходимо использовать переменный ток, а Эдисон – что нужно применять постоянный ток. У второго ученого было больше возможностей, так как он занимался бизнесом, однако Тесла в конечном итоге удалось победить, так как он был попросту прав. ВступлениеПеременный ток значительно эффективнее использовать для передачи энергии. Обсудим, как вычисляется мощность переменного тока, ведь переменный ток - это мощность, которая передается на расстоянии. Вычисление мощностиДопустим, у нас имеется генератор переменного напряжения, который подключен к нагрузке. На выходе генератора, между двумя точками на клеммах, напряжение меняется по гармоническому закону, а нагрузка взята произвольная: катушки, активное сопротивление, конденсаторы, электромотор. В цепи нагрузки течет ток, который меняется по гармоническому закону. Наша задача – установить, чему равна мощность потребляемой нагрузки от генератора. В распоряжении имеем генератор. В качестве исходных данных представлено направление на входе, которое будет меняться по гармоничному правилу: (U(t) = U(m) cos w t) Нагрузка – самое произвольное понятие. Сила тока в нагрузке и, соответственно, в проводах, которые подводят мощность к нагрузке, будет меняться. Частота колебаний тока выйдет такая же, как частота колебаний напряжения, но существует также понятие сдвига фазы в промежутках колебаний тока и напряжения: (I (t) = I (m) cos w t) Дальнейшие вычисленияПоказатели мощность будут равны произведению: P (t) = I (t) U (t) Этот закон остаётся справедливым как для переменного тока с мощностью, которую необходимо было вычислить, так и для постоянного. (I (t) = I (m) cos (wt + J) Мощность переменного тока при переменном токе вычисляется при помощи трех формул. Представленные выше расчеты относятся к основной формуле, которая вытекает из определения силы тока и напряжения. Если участок цепи однородный и можно пользоваться законом Ома для этого участка цепи, здесь такие вычисления использовать нельзя, так как нам неизвестен характер нагрузки. Определяем результатПодставим показатели силы тока и напряжения в данную формулу, и тут нам на помощь придет знание тригонометрических формул: cosa cosb = cos(a +b) + cos(a - b) / 2 Воспользуемся этой формулой и получим вычисления: P(t) = I(m) U (m) cos (wt + J) cos wt После упрощения результатов получим: P(t) = I(m) U (m)/2 cos (wt + J) + I(m) U (m) cosJ Посмотрим на эту формулу. Здесь первое слагаемое зависит от времени, меняясь по гармоническому закону, а второе является величиной постоянной. Мощность переменного тока при переменном токе складывается из постоянной и переменной составляющей. Если мощность положительна, значит, нагрузка потребляет энергию от генератора. При отрицательной мощности, наоборот, нагрузка раскручивает генератор. Найдем среднее значение мощности за период времени. Для этого работу, совершенную электрическим током, поделим на величину этого периода. Мощность трехфазной цепи переменного тока– это сумма переменной и постоянной составляющих. Активная и реактивная мощностьМногие физические процессы можно представить аналогиями друг друга. На этой базе постараемся раскрыть суть понятий активной мощности цепи переменного тока и реактивной мощности цепи переменного тока. Стакан представляет собой электростанцию, вода – электроэнергию, трубочка – кабель или провод. Чем выше поднимается стакан, тем больше напряжение или давление.
Параметры мощности в сети переменного тока активного или реактивного типа зависят от тех элементов, которые потребляют такую энергию. Активная – энергия индуктивности и ёмкости. Покажем это на конденсаторе, ёмкости и стакане. Активными называются те элементы, которые способны преобразовывать энергию в другой вид. К примеру, в тепло (утюг), свет (лампочка), движение (мотор).
Реактивная энергияПри имитации реактивной энергии напряжение увеличивается, и ёмкость заполняется. При уменьшении напряжения накопленная энергия возвращается по проводу обратно в электростанцию. Так повторяется циклически. Сам смысл реактивных элементов заключается в накоплении энергии, которая потом обратно возвращается или используется для других функций. Но никуда не тратится. Основной минус этой производной в том, что виртуальный трубопровод, по которому как-бы идет энергия, имеет сопротивление, и на нем тратится процент экономии. Полной мощности цепи переменного тока требуются затраты определенного процента усилий. По этой причине на крупных предприятиях идет борьба с реактивной составляющей полной мощности. Активная мощность – это та энергия, которая потребляется или преобразуется в другие виды – свет, тепло, движение, то есть в какую-либо работу. ОпытДля опыта возьмем стакан, которые служит активной составляющей мощности. Он представляет часть энергии, которую необходимо потребить или преобразовать в другой вид. Часть энергии воды можно выпить. Полная мощность переменного тока коэффициент мощности - это показатель, который складывается из реактивной и активной составляющих: энергии, текущей по водопроводу и той, которая преобразуется. Как выглядит полная мощность в нашей аналогии? Часть воды выпиваем, а оставшаяся будет продолжать бежать по трубке. Так как у нас есть реактивный ёмкостной элемент – конденсатор или ёмкость, воду опускаем и начинаем имитировать увеличение и уменьшение напряжения. При этом видно, как вода перетекает в двух направлениях. Следовательно, в этом процессе применяется и активная, и реактивная составляющая. Вместе это – полная мощность.
Преобразование мощностиАктивная мощность преобразовывается в другой вид энергии, к примеру, в механическое движение или нагрев. Реактивная мощность, которая накапливается в реактивном элементе, позднее возвращается назад. Полная мощность – это геометрическая сумма активной и реактивной мощности. Для произведения вычислений используем тригонометрические функции. Физический смысл расчетов такой. Возьмем прямоугольный треугольник, в котором одна из сторон равна 90 градусов. Одна из сторон – это его гипотенуза. Есть прилежащий и противолежащий относительно прямого угла катеты. Косинус представлен отношением, которое предопределяет длина прилегающего катета относительно длины гипотенузы.
Синусом угла является вид отношения, которое составляет длина противолежащего катета относительно гипотенузы. Зная угол и длину любой из сторон, можно вычислить все остальные углы и длину. В данном треугольнике можно взять длину гипотенузы и прилежащего катета и вычислить этот угол с помощью тригонометрической функции косинусов. Мощность постоянного и переменного тока вычисляется с применением таких знаний. Для вычисления угла можно применять обратную функцию от косинуса. Получим необходимый результат вычислений. Чтобы вычислить длину противолежащего катета, можно вычислить синус и получить соотношение противолежащего катета к гипотенузе. Вычисление мощности цепи переменного тока по формуле предложено в этом описании. В цепях постоянного тока мощность равна произведению напряжения на ток. В цепях переменного тока также работает это правило, но его трактовка будет не совсем правильной. ИндуктивностьПомимо активных элементов, действуют реактивные элементы – индуктивность и ёмкость. В цепях постоянного тока, где амплитудное значение напряжения токов не меняется во времени, работа данного сопротивления будет происходить только во времени. Индуктивность и ёмкость могут негативным образом влиять на сеть. Активная мощность, которую имеет трехфазная цепь переменного тока, может выполнять полезную работу, а реактивная не выполняет никакой полезной работы, а только расходуется на преодоление реактивных сопротивлений индуктивности и ёмкости. Попытаемся выполнить опыт. Возьмем источник переменного напряжения на 220 Вт с частотой 50Гц, датчик напряжения и тока источника, нагрузка, которая составляет активное 1Ом и индуктивное 1ОМ сопротивление. Также есть выключатель, который подключится в определенный момент, активно-ёмкостная нагрузка. Запустим такую систему. Для удобства рассмотрения введем коэффициенты поправки напряжения. Запускаем устройствоПри запуске устройства видно, что напряжение и ток сети не совпадают по фазе. Наблюдается переход через 0, при котором существует угол – коэффициент мощности сети. Чем меньше этот угол, тем выше коэффициент мощности, который указывается на всех устройствах переменного тока, к примеру, электрических машинах или сварочных трансформаторах. Угол зависит от величины индуктивного сопротивления нагрузки. Когда сдвиг уменьшается, увеличивается ток сети. Представим, что сопротивление катушки уменьшить нельзя, но надо улучшить косинус сети. Для этого и нужны конденсаторы, которые, в отличие от индуктивности, опережают напряжение и могут взаимно компенсировать реактивную мощность. В момент подключения конденсаторной батареи за 0,05 с происходит резкое снижение косинуса, практически до 0. Также идет резкое снижение тока, который без конденсаторной батареи имел амплитудное значение намного ниже, чем при включении конденсаторной батареи.
Фактически подключением конденсаторной батареи удалось снизить мощность тока, потребляемого из сети. Это является положительным моментом и позволяет снижать ток сети и экономить на сечение кабелей, трансформаторах, силовом оборудовании. Если произойдет отключение индуктивной нагрузки и останется активное сопротивление, произойдет процесс, когда косинус сети после подключения конденсаторной батареи приведет к фазовому сдвигу и большому скачку тока, который идёт в сеть, а не потребляется из неё, что происходит в генераторном режиме реактивной мощности. ИтогиАктивная мощность опять остается постоянной и равна нулю, так как нет индуктивного сопротивления. Начался процесс генерации реактивной мощности в сеть. Следовательно, компенсировать реактивную мощность на крупных предприятий, потребляемых колоссальные её объёмы из энергосистем, - это приоритетная задача, так как это позволяет экономить не только на электрооборудовании, но и на затратах по оплате самой реактивной мощности. Такое понятие регламентируется, и предприятие оплачивает и потребляемую, и генерируемую мощность. Здесь устанавливаются автоматические компенсаторы, обеспечивающие поддержку баланса мощности на заданном уровне. При отключении мощной нагрузки, если не выключить из сети компенсирующее устройство, будет происходить генерация реактивной мощности в сеть, что создаст проблемы в энергосистеме. В быту компенсация реактивной мощности не имеет смысла, так как потребление мощности здесь значительно ниже. Активная и реактивная мощность – понятия школьного курса физики. fb.ru Мощность переменного тока - fiziku5.ru
Энергия в катушке индуктивности не расходуется. В первую четверть периода она запасается в ее магнитном поле, а во вторую — отдается источнику тока. Произведение напряжения UL на величину силы тока I в цепи называется реактивной мощностью. В рассмотренной цепи активная мощность равна нулю, так как энергия в ней не расходуется, сдвиг по фазе между векторами тока I и напряжением U равен 90 ° и cos φ = 0. Переменный ток в цепи с последовательными активным и индуктивным сопротивлениями. Теперь рассмотрим цепь с реальной катушкой, которую можно представить как цепь с последовательно включенными индуктивностью L и активным сопротивлением R (рис. 1.7). Если в цепи с последовательными активным и индуктивным сопротивлениями протекает переменный синусоидальный ток, то напряжение на индуктивности, как было установлено ранее, опережает ток на 90°, а напряжение на активном сопротивлении Так как напряжения UL, UR по фазе не совпадают, то напряжение, приложенное ко всей цепи, равно их геометрической сумме. Сложив векторы UL и UR, находим величину вектора U, который сдвинут по фазе относительно вектора тока I на угол φ < 90°, опережая его. Таким образом, в цепи переменного тока с последовательно соединенным активным сопротивлением и катушкой индуктивности ток отстает по фазе от напряжения. Построив векторную диаграмму, рассмотрим треугольник со сторонами UL, UR, U. Этот треугольник называется треугольником напряжений. Так как он прямоугольный, то
Из треугольника напряжений можно получить подобный ему треугольник сопротивлений со сторонами R, XL и Z Из этого треугольника полное сопротивление цепи равно:
Так как сдвиг по фазе между током и напряжением меньше 90°, то энергия в такой цепи расходуется лишь на активном сопротивлении R. Активная мощность при этом равна:
Цепь переменного тока с емкостью. Если к источнику переменного тока подключить конденсатор, то в цепи появится ток. Способность конденсатора пропускать переменный ток объясняется тем, что под действием переменного синусоидального напряжения конденсатор периодически заряжается и разряжается, вследствие чего происходит перемещение электрических зарядов в проводниках, соединяющих конденсатор с источником тока. Соотношение фаз тока и напряжения представлено на рис. 1.8. В и, епи с емкостью ток опережает по фазе напряжение на 90°. Закон Ома для цепи переменного тока с емкостью определяет действующее значение силы тока:
Величина 1.9. Мощность переменного тока Для цепей переменного тока различают активную, полную и реактивную мощности. Активная мощность представляет собой действительную мощность переменного тока, аналогичную мощности, развиваемой постоянным током. Она производит полезную работу; может быть преобразована с помощью электродвигателей в механическую мощность, механическую энергию; измеряется в ваттах (Вт) и определяется по формуле
(1.23) Полной мощностью называют максимально возможную величину активной мощности, развиваемую переменным током при заданных значениях напряжения и силы тока и при наиболее благоприятных условиях, а именно, когда cos φ = 1. Полная мощность обозначается латинской буквой S и измеряется в вольт-амперах (В-А). Из определения полной мощности следует выражение
(1.24)
(1.25) (1.26) Полной мощностью (кВ А) принято измерять мощность генераторов переменного тока, машин, производящих электроэнергию, и трансформаторов, аппаратов, предназначенных для преобразования электрической энергии одного напряжения в электрическую энергию другого напряжения. Полная мощность этих машин определяется произведением номинальных (нормальных) величин их напряжения и силы тока (т. е. величин этих параметров, на которые рассчитаны машины). А активная их мощность зависит от коэффициента мощности, при котором они работают (Р= Scosφ). В свою очередь этот коэффициент мощности зависит от соотношения величин активного и реактивного сопротивления, включенных в цепь, иными словами, от характера электроприемников, питаемых данным генератором или трансформатором. Реактивная мощность. Для рассмотрения реактивной мощности необходимо иметь представление об активной и реактивной составляющих переменного тока. Сравнивая между собой формулы для определения мощности переменного и постоянного тока, можно видеть, что на месте полной величины силы тока I в формуле мощности стоит выражение I cos φ, где cos φ — величина, меньше единицы (и только в отдельных случаях равная ей). Отсюда следует, что в цепях переменного тока не весь ток создает полезную, активную мощность, а только некоторая его часть, которая называется активной составляющей тока. Проекция вектора тока на горизонтальное направление, перпендикулярное вектору напряжения, равная /sin<p, называется реактивной составляющей переменного тока. Реактивная составляющая тока не участвует в создании активной мощности. Произведение действующего в цепи напряжения на реактивную составляющую тока носит название реактивной мощности и обозначается латинской буквой Q. Реактивная мощность измеряется в единицах, называемых «вар». Из приведенного определения реактивной мощности вытекает соотношение
где Q — реактивная мощность, вар; U — напряжение, В; I — сила тока, A; sin φ — числовой коэффициент, зависящий от угла сдвига фаз в данной цепи. Реактивная мощность, так же как и реактивная составляющая тока, характеризует собой ту энергию, которая идет на создание магнитного поля индуктивности или электрического поля конденсатора (если последний включен в данную цепь). Эта энергия в процессе протекания переменного тока в цепях со сдвигом фаз совершает непрерывные колебания между источником энергии и ее потребителем. Активная, реактивная и полная мощности переменного тока связаны между собой соотношением
Это соотношение можно представить как векторную диаграмму, получаемую на основании диаграммы напряжений или токов, носящую название «треугольника мощностей» (рис. 1.9). Два катета этого треугольника представляют собой в том или ином масштабе активную и реактивную мощности (соответственно в кВт и квар), а гипотенуза — полную мощность (в кВ-А). Угол ср численно равен углу сдвига фаз тока и напряжения в цепи. Значение косинуса этого угла называют коэффициентом мощности. 1.10. Понятие о трехфазном токе и его получении Трехфазной системой называется совокупность трех однофазных цепей, в которых действуют три ЭДС одинаковой частоты, сдвинутые по фазе одна относительно другой на 120°. Такая система получила наиболее широкое распространение, ибо она позволяет при передаче одной и той же мощности получить экономию металла в проводах, уменьшить потери энергии и создать простые и удобные в эксплуатации трехфазные двигатели переменного тока. На рис. 1.10 показана система, состоящая из трех отдельных генераторов (рис. 1.10, б), и упрощенная схема генератора трехфазного тока (рис. 1.10, а). Трехфазный генератор имеет три обмотки, в которых индуктируются три ЭДС, сдвинутые по фазе на 120°. Каждая обмотка называется фазой, а напряжение на фазе — фазным напряжением (£/ф). Нагрузка подключается к обмоткам генератора линейными проводами и нулевым проводом, который в некоторых случаях может отсутствовать. Напряжение между линейными проводами называется линейным напряжением (Un). Ток в фазе генератора или нагрузки называется фазным током, а ток в линейном проводе — линейным током. Обмотки генератора и нагрузка могут включаться в «звезду» или в «треугольник». На рис. 1.11 показано соединение в «звезду»: начало или
концы обмоток генератора соединяют в одну точку. К оставшимся концам обмоток подключают линейные провода, а к общей точке — нулевой провод. Если нагрузка равномерная, то нулевой провод не нужен, ибо он обеспечивает независимость работы фаз при неравномерной нагрузке, когда по нему текут уравнительные токи. Линейное напряжение при соединении в «звезду» в — Д раз больше фазного, линейные и фазные токи одинаковы:
Чтобы соединить обмотки генератора в «треугольник», необходимо конец первой обмотки соединить с началом второй; конец второй — с началом третьей; конец третьей — с началом первой. Линейные провода подключают к точкам соединения фаз (рис. 1.12).
При соединении в «треугольник» линейные и фазные напряжения равны, а линейный ток в 7з раз больше фазного:
Мощность трехфазной системы складывается из мощностей каждой фазы. Чтобы найти общую мощность, надо по формуле Р=IФUФcosφ определить мощность в каждой фазе и все три мощности сложить. Так поступают при любых нагрузках. Общая мощность может быть определена по формуле
(1.31) если нагрузка равномерная, т. е. если сопротивление и характер нагрузки всех трех фаз одинаковы. 1.11. Электроизмерительные приборы Электроизмерительными приборами называются приборы, служащие для измерения электрических величин. Они классифицируются по следующим признакам: по роду измеряемой величины: амперметры, вольтметры, омметры, ваттметры и комбинированные; по роду тока: приборы постоянного тока, переменного тока и комбинированные; по принципу действия: магнитоэлектрические, электромагнитные, электродинамические, индукционные, термоэлектрические, электростатические, электронные и др.; по погрешностям измерений: на восемь классов — 0,05; 0,1; 0,2; 0,5; 1; 1,5; 2,5 и 4. Цифры показывают максимальную погрешность в процентах, которая возможна у прибора данного класса. Например, погрешность показаний амперметра класса 1,5 не превышает ±1,5%. Существует два основных метода электрических измерений: метод непосредственной оценки; метод сравнения. В методе непосредственной оценки измеряемая величина отсчитывается непосредственно по шкале прибора. Достоинство метода — удобство отсчета показаний прибора и малая затрата времени на операцию измерения. Недостаток — сравнительно невысокая точность измерений. В методе сравнения измеряемая величина сравнивается непосредственно с эталоном. Метод сравнения используется в лабораторных условиях. Кроме обычных показывающих приборов, которые указывают то или иное измерение на данный момент времени (обычно стрелкой на шкале прибора) существуют самопишущие измерительные приборы, записывающие непрерывно на движущейся ленте свои показания. Условные обозначения, определяющие основные характеристики прибора, выносятся на шкалу электроизмерительного прибора (табл. 1.1). Таблица 1.1 Основные условные обозначения, выносимые на шкалу электроизмерительного прибора
Пример. На шкале прибора имеются следующие условные обозначения: 2,5; ГЛАВА 2. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ 2.1. Общие сведения Электрические машины, действия которых основаны на электромагнитных явлениях и которые служат для преобразования механической энергии в электрическую, называют электромашинными генераторами, а преобразующие электрическую энергию в механическую — электродвигателями. Применяют также электрические машины для преобразования электрической энергии одних параметров в другие, которые называют преобразователями. Преобразовываться могут: род тока, частота, напряжение, число фаз и другие параметры электроэнергии. Электрические генераторы приводятся во вращение паровыми и водяными турбинами, двигателями внутреннего сгорания и др. Электродвигатели служат для приведения в действие станков, различных машин, транспортного оборудования и др. К электрическим машинам относят трансформаторы — статические аппараты, не имеющие движущихся частей, но по своему устройству и принципу действия имеющие много общего с электрическими машинами. Электрические машины обладают свойством обратимости, т. е. могут работать генератором. Если их вращать каким-либо двигателем или подводить к ним электроэнергию, они могут использоваться как электродвигатели. Однако при проектировании электромашин учитывают требования, предъявляемые особенностями их работы генератором или электродвигателем. Электрические машины подразделяются на машины переменного и постоянного тока. Электрические машины переменного тока разделяют на синхронные, асинхронные, коллекторные. Наибольшее применение имеют синхронные генераторы переменного трехфазного тока и трехфазные асинхронные электродвигатели. Коллекторные электродвигатели переменного тока имеют ограниченное применение вследствие сложности устройства, обслуживания и более высокой стоимости. Основным их преимуществом является возможность регулирования скорости вращения в широких пределах, что затруднительно в асинхронных двигателях. fiziku5.ru Мощность переменного токаПеременный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока. Пусть U и I мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени dt настолько малый, что напряжение и ток не успеют за это время сколько-нибудьизмениться; иными словами, величины U и I можно считать постоянными в течение интервала dt. Пусть за время dt через наш участок прошёл заряд dq = Idt (в соответствии с правилом выбора знака для силы тока заряд dq считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу dA = Udq = UIdt: Мощность тока P это отношение работы электрического поля ко времени, за которое эта
Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (118) называется ещё мгновенной мощностью. Из-заналичия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая. 1.Мощность положительна: P > 0. Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается). 2.Мощность отрицательна: P < 0. Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток. Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы ¾перевешивает¿ поле движущихся зарядов и ¾продавливает¿ ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается). Если вы не вполне поняли, о чём только что шла речь, не переживайте дальше будут конкретные примеры, на которых вы всё и увидите. 24.1Мощность тока через резисторПусть переменный ток I = I0 sin !t протекает через резистор сопротивлением R. Напряжение на резисторе, как нам известно, колеблется в фазе с током: U = IR = I0R sin !t = U0 sin !t: Поэтому для мгновенной мощности получаем: P = UI = U0I0 sin2 !t; studfiles.net Мощность переменного тока - материалы для подготовки к ЕГЭ по ФизикеАвтор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока. Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала . Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена: (1) Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью. Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая. 1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается). 2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток. Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается). Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите. Мощность тока через резисторПусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током: Поэтому для мгновенной мощности получаем: (2) График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.
Рис. 1. Мощность переменного тока через резистор Максимальное значение На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта: среднее значение квадрата синуса (или косинуса) за период равно Этот факт иллюстрируется рисунком 2.
Рис. 2. Среднее значение квадрата синуса равно Итак, для среднего значения мощности тока на резисторе имеем: (3) В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»): (4) Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока: Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко. Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые Мощность тока через конденсаторПусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на : Для мгновенной мощности получаем: График зависимости мгновенной мощности от времени представлен на рис. 3.
Рис. 3. Мощность переменного тока через конденсатор Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой. Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).
Рис. 4. Напряжение на конденсаторе и сила тока через него Рассмотрим последовательно все четыре четверти периода. 1. Первая четверть, Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор. 2. Вторая четверть, Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать). 3. Третья четверть, Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию. 4. Четвёртая четверть, Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные. Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой. Мощность тока через катушкуПусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на : Для мгновенной мощности получаем: Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).
Рис. 5. Напряжение на катушке и сила тока через неё Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки. В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке. Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю. Мощность тока на произвольном участкеТеперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки...На этот участок подано переменное напряжение . Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так: Тогда для мгновенной мощности имеем: (5) Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу: В результате получим: (6) Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной: (7) Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока: Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю. Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи. С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы. Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве) Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним. ege-study.ru Мощность переменного тока. Работа переменного токаГоспода, всех вас в очередной раз приветствую! В сегодняшней статье я бы хотел поднять темы, касающиеся мощности и энергии (работы) в цепях переменного тока. Сегодня мы узнаем, что это такое и научимся их определять. Итак, погнали. Прежде чем начать что-либо обсуждать про переменный ток, давайте-ка вспомним, как мы определяли мощность в случае постоянного тока. Да-да, у нас была отдельная статейка на эту тему, помните? Если нет, то напоминаю, что в случае постоянного тока мощность в цепи считается очень просто, по одной из этих трех замечательных формул:
где P – искомая мощность, которая выделяется на резисторе R; I – сила тока в цепи через резистор R; U – напряжение на резисторе R. Это все здорово. Но как быть в случае переменного тока, а в частности – синусоидального? Ведь там у нас колбасится синус, значения тока и напряжения все время меняются, сейчас они одни, через мгновение – уже другие, т.е., выражаясь научным языком, они являются функциями времени. Пользуясь знаниями, полученными нами в предыдущей вводной статье, мы можем записать вот такой закон изменения силы тока:
Мы не будем сейчас повторять что здесь есть что, все это было досконально рассмотрено в прошлый раз. Абсолютно аналогично можно записать зависимость напряжения от времени для переменного синусоидального тока
Пока что считаем, что у нас в цепи только резисторы (конденсаторы и индуктивности отсутствуют), следовательно, напряжение и ток совпадают по фазе между собой. Не понятно почему так? Ничего, в будущем разберем это подробно. Пока же для нас это значит только то, что фазы как в законе изменения тока, так и в законе изменения напряжения можно выкинуть. И вот глядя на эти три строчки с формул и сопоставляя их между собой, не приходит ли вам на ум какая-либо идея? Например, что можно бы подставить ток или напряжение в формулу для мощности... Такая идея пришла? Это просто замечательно! Давайте ее сейчас же реализуем! Поскольку у нас и ток, и напряжения зависят от времени, все три полученные новые формула для мощности абсолютно также будет зависеть от времени.
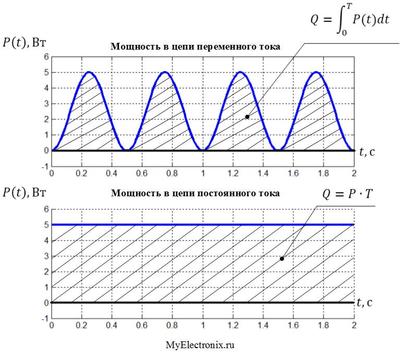
Ох, прям в глазах рябит от синусов Итак, с мощностью более-менее понятно. А как быть с энергией? Ну, то есть с теплом, которое выделяется на резисторе? Как оценить эту самую энергию? Для этого нам надо вспомнить, как же связаны между собой мощность и энергия. Мы уже затрагивали эту тему в статье про мощность в цепи постоянного тока. Тогда этот вопрос решился просто: при постоянном токе достаточно умножить мощность (которая там не зависит от времени и все время одинакова) на время наблюдения и получить выделяющуюся за это самое время наблюдения энергию. С переменным током все посложнее, потому что тут мощность зависит от времени. И, увы, тут не обойтись без интегралов… Что это вообще такое этот самый интеграл? Как, вероятно, многие из вас знают, интеграл – это просто площадь под графиком. В данном конкретном случае под графиком зависимости мощности от времени P(t). Да, вот так вот все просто. Итак, энергия (или работа, что по сути одно и то же) в цепи переменного тока считается следующим образом
В этой формуле Q – это искомая работа (энергия) переменного тока (измеряется все так же в джоулях), P(t) – закон изменения мощности от времени, а Т – собственно, сам отрезок времени, который мы рассматриваем, и в течении которого ток работает. Вообще говоря, это выражение можно рассматривать как общий случай и для постоянного тока, и для переменного (при этом переменный ток может быть любой формы, не обязательно синусоидальный). Во всех эих случаях можно считать энергию через вот этот вот интеграл. Если же мы подставим сюда P(t)=const (случай постоянного тока), то исходя из особенности взятия интеграла от константы результат расчета будет абсолютно таким же, как если бы мы просто умножили мощность на время, поэтому нет никакого смысла так заморачиваться и рассматривать интегралы в теме постоянного тока. Но полезно это знать, что бы была некая единая картина. Сейчас же, господа, я прошу вас запомнить главный вывод из всей этой болтовни – если мы хотим найти выделившуюся энергия за время T (без разницы какой ток – постоянный или переменный), то это можно сделать, найдя площадь под графиком зависимости мощности от времени на интервале от 0 до Т. Если брать токи синусоидальные и подставлять конкретные выражения для зависимости мощности от времени, то энергию можно посчитать по одной из следующих формул
Господа, скажу сразу, в своих статьях я не буду рассказывать, как брать интегралы. Я надеюсь, что вы это знаете. А если нет – ничего страшного, не спешите закрывать статью. Я буду стараться строить изложение таким образом, чтобы незнание интегралов не привело в вашем сознании к fatal error Давайте теперь разберем все вышесказанное на конкретном примере. Господа, специально для вас я подготовил рисуночек 1. Взгляните на него. Изображение кликабельно.
Рисунок 1 – Зависимость мощности от времени для переменного и постоянного тока Там два графика: на верхнем показана зависимость мощности от времени для случая переменного синусоидального тока, а на нижнем – для случая постоянного тока. Как я их построил? Очень просто. Для первого графика я взял вот эту ранее написанную нами формулу.
Будем полагать, что амплитуда синусоидального тока равна Im=1 A, сопротивление резистора, на котором рассеивается мощность, равно R=5 Ом, а частота синуса равна f = 1 Гц, что соответствует круговой частоте
То есть формула, по которой мы строим график мощности переменного тока, имеет вид
Именно по этой формуле построен верхний график на рисунке 1. А как быть с нижним графиком? Господа, ну тут совсем все просто. Я исходил из того, что через тот же самый резистор R=5 Ом течет постоянный ток величиной I=1 А. Тогда, как должно быть понятно из закона Джоуля-Ленца, на данном резисторе будет рассеиваться вот такая вот мощность
Поскольку ток постоянный, то эта мощность будет одинаковой в любой момент времени. А для таких замечательнейших случаев эталонной стабильности великая и могучая математика предусматривает график в виде прямой. Что мы и видим на нижнем графике рисунка 1. Понятное дело, что раз через наши пятиомные резисторы течет ток, то на них выделяется некоторая мощность и рассеивается некоторое количество энергии. Иными словами, резистор греется за счет выделяющейся на нем энергии. Мы уже обсуждали, что эта энергия считается через интеграл. Но, как мы уже говорили, есть и графическое представление этого интеграла – он равен площади под графиком. Эту площадь я заштриховал на рисунке 1. То есть, если мы найдем, чему равна площадь под верхним и нижним графиками, то мы определим, какое количество энергии выделилось в первом и втором случае. Ну, с нижним графиком вообще все просто. Там – прямоугольник высотой 5 Вт и шириной 2 секунды. Поэтому площадь (то бишь энергия) находится элементарно
Отметим, что этот результат в точности совпадает с формулой, полученной нам для расчета энергии постоянного тока в одной из прошлых статей. Со верхним графиком все не так просто. Там у нас неправильная форма и просто так сразу нельзя сказать, чему равна эта площадь. Вернее, сказать можно – она равна вот такому вот интегралу
Результат вычисления этого интеграла равен конкретному числу и это число – как раз наша искомая энергия, которая выделилась на резисторе. Мы не будем расписывать взятие этого интеграла. Посчитать такой интеграл ручками не составит труда для человека, хотя бы поверхностного знакомого с математикой. Если же все-таки это вызывает затруднение, или просто лень самому считать – есть огромное количество САПРа, которое сделает это за вас. Либо можно посчитать этот интеграл на каком-либо сайте: по запросу в гугле «интегралы онлайн» выдается достаточное количество результатов. Итак, сразу переходим к ответу и он равен
Вот так вот. Энергия, которая выделяется на резисторе при протекании синусоидального тока с амплитудой 1 А почти в два раза меньше энергии, которая будет выделяться в случае, если течет постоянный ток величиной 1 А. Оно и понятно – даже визуально на рисунке 1 площадь под верхним графиком заметно ниже, чем под нижним. Как-то так, господа. Теперь вы знаете, как рассчитать мощность и энергию в цепи переменного тока. Однако сегодня мы рассмотрели довольно сложный путь. Оказывается, есть методы попроще, с использованием так называемых действующих величин тока и напряжения. Но об этом в следующей статье. А пока что – всем вам огромной удачи, спасибо, что прочитали, и пока! Вступайте в нашу группу Вконтакте Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it. myelectronix.ru Мощность в цепях переменного тока13 МОЩНОСТИ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
В большинстве случаев электрические цепи содержат как активное, так и реактивное сопротивления. К такого рода цепям относятся, в частности, двигатели переменного тока, трансформаторы и другие устройства. В этих цепях между напряжением U и током I существует сдвиг фаз . Если к цепи приложено синусоидальное напряжение
то ток в цепи
Мгновенная мощность цепи
Выражение, стоящее в квадратных скобках, можно на основании тригонометрической формулы представить как разность косинусов
Таким образом,
Среднее значение мгновенной мощности за период равно UL cos , так как среднее значение соs (2wt — ) за период равно нулю. Следовательно, активная мощность цепей переменного тока определяется в общем случае формулой
Множитель соs называют коэффициентом мощности. Учитывая, что получаем
Активная мощность измеряемся в ваттах (вт) или в киловаттах (квт).
Произведение Рt называется активной энергией и измеряется в втсек или в квт ч: 1 квт ч = 3800 втсек (дж). Активная энергия, потребляемая электрической цепью, полностью преобразуется в тепло в активном сопротивлении этой цепи и обратно к источнику не возвращается. Если величины сторон треугольника сопротивлений (рис. 165, а) умножить на величину I2 (рис. 165, б), то получим треугольник мощностей (рис. 165, в). Все стороны этого треугольника показанногоотдельно на рис. 166, представляют собой мощности. Катет, прилегающий к углу , представляет собой известную нам активную мощность Р:
Активная мощность в цепях переменного тока преобразуется в тепло. В двигателях переменного тока большая часть активной мощности превращается в механическую мощность, остальная Часть также преобразуется в тепло. Катет, лежащий против угла , есть реактивная мощность Q:
Реактивная мощность обусловлена наличием магнитных и электрических полей в электрических цепях. Как уже указывалось, реактивная мощность характеризует интенсивность обмена энергией между источником, с одной стороны, и магнитными и электрическими полями — с другой. Реактивная мощность измеряется в вольт-амперах реактивных (вар) или киловольт-амперах реактивных (тар). Гипотенуза треугольника мощностей представляет собой полную мощность S:
Она измеряется в вольт-амперах (ва) или киловольт-амперах (ква). Величина полной мощности равная произведению UI, определяет основные габариты (наибольшие размеры) генераторов и трансформаторов. В самом деле, величина тока I определяет необходимое по условиям нагрева сечение проводов генераторов и трансформаторов, а число витков обмоток, их изоляция, а также размеры магнитопроводов пропорциональны величине напряжения U.
Таким образом, чем больше значения U и I, на которые рассчитываются генераторы и трансформаторы, тем больше должны быть их размеры. Рассмотрим электрическую цепь, показанную на рис. 167, в которую входят индуктивное и активное сопротивления и измерительные приборы — амперметр, вольтметр и ваттметр. Об устройстве ваттметра будет рассказано далее (см. главу одиннадцатую).
1. Если подключить эту цепь к постоянному напряжению U = 120 в, то, поскольку индуктивное сопротивление xL при постоянном токе будет равно нулю, в цепи остается одно активное сопротивление r и тогда
Амперметр покажет ток 5 а. Мощность
или
Ваттметр покажет 600 вт. Показание ваттметра, включенного в цепь постоянного тока, равно произведению показаний вольтметра и амперметра. 2. Подключим ту же цепь к переменному напряжению U= 120в. В этом случае
Ток в цепи
Амперметр покажет ток 4 а. Подсчитаем мощность, идущую на нагрев:
Действительно, активная мощность, потребляемая цепью, равна
Показание ваттметра в этом случае будет 384 вт. Полная мощность
Следовательно, генератор, питающий эту цепь, отдает полную мощность S = 480 ва. Но в самой цепи только активная мощность Р = 384 вт. безвозвратно преобразуется в тепло. Отсюда видно, что цепь переменного тока, содержащая наряду с активным сопротивлением индуктивное, из всей получаемой ею энергии только часть расходует на тепло. А остальная часть — реактивная энергия — то поступает в цепь от генератора и запасается в магнитном поле катушки, то возвращается обратно генератору. Баланс мощностей в цепях переменного тока Коэффициент мощности Генератор или электрооборудование энергетически выгодно эксплуатировать, если оно совершает максимальную работу. Работа в электрической цепи определяется активной мощностью Р. Коэффициент мощности показывает, насколько эффективно используется генератор или электрооборудование λ=P/S=cosφ≤1 С уменьшением коэффициента мощности стоимость потребляемой электроэнергии возрастает . Способы увеличения коэффициента мощности Мощность максимальна в случае, когда Р = S, т.е. в случае резистивной цепи. Генератор осуществляет только необратимые преобразования энергии и не участвует в колебательных процессах обмена энергией с электромагнитным полем приемников, в режиме максимальной мощности. Потребители электрической энергии в основном имеют схему замещения RL элемента, поэтому увеличение коэффициента мощности возможен с помощью компенсации реактивной мощности подключением емкостного элемента (QL-QС), подключение емкостного элемента снижает ток в линии электропередачи, что позволяет уменьшить сечение электропроводов, а это приводит к экономии электропроводящих материалов. Значение коэффициента мощности в энергосистемах зависит насколько грамотно эксплуатируется электротехнические установки и приборы. сosφ может снижаться, если установки работают в режиме холостого хода, или недогружены. studfiles.net Мощность переменного тока - Основы электроникиМы знаем, что в цепях переменного тока между током и напряжением может возникнуть разность фаз. Как же вычислить мощность переменного тока в этом случае, когда направления радиусов-векторов тока и напряжения не совпадают? Представим себе, что мы тянем вагонетку с грузом, катящуюся по рельсам. Но наши усилия направлены не как обычно, вдоль рельсов, а под некоторым углом к ним. Угол между направлением движения вагонетки и направлением наших усилий обозначим буквой φ (фи). Ясно, что при таком способе передвижения вагонетки часть наших сил будет затрачиваться бесполезно, не производя работы, то есть работа не будет равна произведению приложенной силы на пройденный путь, как обычно (работа = сила * путь),
а будет меньше этого произведения. Для того чтобы вычислить количество произведенной работы, нужно силу, приложенную к вагонетке, разложить на две части или на две составляющие. Это разложение силы сделано на рисунке 1. Составляющая силы, направленная вдоль движения, которая называется проекцией силы на направление движения, будет полезной силой, а, составляющая, направленная под прямым углом к направлению движения, будет силой бесполезной.
Если стрелка (вектор), изображающая силу, вычерчена в масштабе, то, измерив полезную составляющую силы, мы можем определить количество работы: работа = полезная сила * путь.
Теперь обратимся к радиусам-векторам тока и напряжения. Здесь полностью применим тот же самый метод. Мощность переменного тока при разности фаз φ = 0° будет равна половине произведения вектора напряжения Um и вектора тока Im.
Тогда мощность переменного тока, при разности фаз φ не равной нулю, будет равна половине произведения вектора напряжения Um и проекции вектора тока Imп, проецируемого на вектор напряжения (рисунок 2). Как нетрудно видеть, величина проекции зависит, во-первых, от длины проецируемого вектора, а во-вторых, от угла между ним и направлением, на которое он проецируется.
Если обозначить этот угол буквой φ, то длина проекции будет равна длине проецируемого вектора, умноженной на особый коэффициент, характеризующий этот угол, называемый косинусом угла (cos φ ). Значения косинусов различных углов приведены в таблице.
Итак, проекция радиуса-вектора равна длине радиуса-вектора, умноженной на cos φ. И, следовательно, мощность переменного тока равна:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! Похожие материалы:Добавить комментарийwww.sxemotehnika.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||
|
|
|||||||||||||||||
|
(1.18)
(1.19)
(1.20)
(1.21)
(1.22)
называется емкостным сопротивлением. Она обратно пропорциональна частоте тока в цепи и емкости конденсатора. Измеряется в омах (Ом).
Сравнивая между собой формулы (1.23) и (1.24), находим соотношение между активной и полной мощностями:
(1.27)
(1.28)
(1.29)
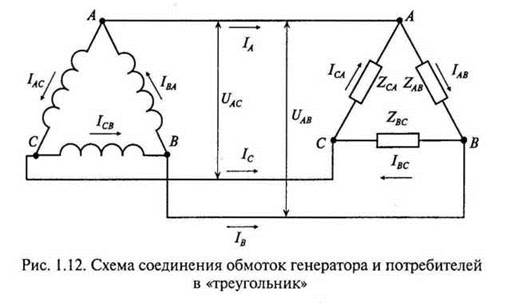
(1.30)
;
;
;
; Б. Это значит, что погрешность при из мерении — 2,5%; род тока — постоянный и переменный; электромагнитная измерительная система; вертикальная установка; изоляция испытана при напряжении 2 кВ; прибор предназначен для установки в закрытых неотапливаемых помещениях.
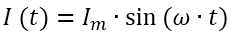
. Но ведь все довольно просто и очевидно откуда, что получилось, не так ли? По вот этим вот самым формулам можно рассчитать мгновенную мощность в определенный момент времени. Фишка в том, что если через резистор течет переменный ток, то в каждое мгновение времени на нем будет выделяться вообще говоря разная мощность: иначе и быть не может, раз амплитуда тока через резистор все время разная. Другое дело, что визуально, при большой частоте изменения тока, мы скорее всего это не заметим: температура резистора не будет хаотично скакать в такт изменения мощности, которая на нем выделяется. Это будет потому, что сам резистор благодаря его массе и теплоемкости синтегрирует эти перепады температуры.
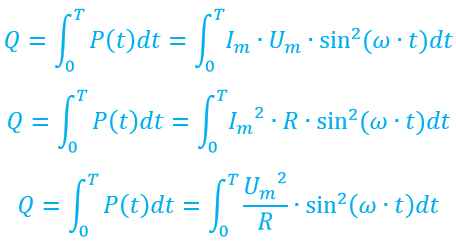
. Очень часто их вообще не требуется считать ручками, а можно посчитать в специализированных программах или даже онлайн на многочисленных сайтах.
