Большая Энциклопедия Нефти и Газа. Круговой ток
ens.tpu.ru Магнитное поле кругового тока | Все формулыМагнитное поле кругового тока — Создается током текущему по тонкому круглому проводу
Вывод формулы для магнитного поля кругового тока : Поскольку расстояние всех элементов проводника до центра кругового тока одинаково и равно R и все элементы проводника перпендикулярны радиусу-вектору (sinα=1), то
Тогда у нас получается
Решив интеграл, у нас получается формула для магнитного поля кругового тока
Так же есть : Магнитное поле прямого тока: В Формуле мы использовали :
xn--b1agsdjmeuf9e.xn--p1ai 6 Магнитное поле прямого и кругового токов.1 Магнитостатика – раздел классической электродинамики, изучающий взаимодействие постоянных токов посредством создаваемого ими постоянного магнитного поля и способы расчета магнитного поля в этом случае. Магнитное поле – силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом. 2 Сила Лоренца – сила, действующая на заряженную частицу, движущуюся в электромагнитном поле. Fm – сила, действующая на движущийся точечный заряд q в магнитном поле. Вектор В называется напряженностью магнитного поля, v – скорость частицы, с – постоянная, выбор ее значения и размерности определяется системой единиц. Измерим силу, когда заряд движется перпендикулярно к В со скоростью , умножив векторно на , учитывая, получим
В электрическом поле , так как при действии электрического и магнитного полей, сила действующая на частицу складывается из магнитной и электрической составляющих. 4 Закон Био-Савара - закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током Поднесем заряд к магниту на подвесе. Магнитное поле пропорционально скорости движения частицы. Чем больше заряд, тем сильнее отклонение, а также магнитное поле обратно пропорционально квадрату расстояния. r – радиус-вектор проведенный от заряда к точке наблюдения, с- постоянная зависящая от выбора системы единиц - электрическое поле неподвижного заряда
В гауссовой системе единиц величины В и Е имеют одинаковую размерность. Постоянная с' для простоты выбирается равной с, с – электродинамическая постоянная, по измерениям она совпадает со скоростью света в вакууме. или - закон Био-Савара для объемного элемента с током - для линейного Опытной проверке доступна только интегральная форма закона Био-Савара, так как выражения применимы для постоянных токов, а постоянные токи замкнуты, следовательно, невозможно выделить отдельные участки постоянных токов и экспериментировать с ними. 5 Принцип суперпозиции для магнитного поля магнитные поля отдельных движущихся зарядов векторно складываются, причем каждый заряд возбуждает поле, совершенно не зависящее от наличия других зарядов. Магнитное поле прямого тока, т е тока текущего по прямому проводу бесконечной длины - магнитное поле элемента тока ,dl – элемент длины провода
- проинтегрировав в этих пределах последнее выражение получим магнитное поле равное: -магнитное поле прямого тока от всех элементов тока будет образовываться конус векторов , результирующий вектор направлен вверх по осиZ. Сложим проекции векторов на осьZ, тогда каждая проекция имеет вид: угол между и радиус вектором r равен . Интегрируя по dl и учитывая , получим - магнитное поле на оси кругового витка
7 Линии напряженности магнитного поля – Силовые линии магнитного поля – окружности. Линиями магнитного поля линии, проведенные так, что касательные к ним в каждой точке указывают направление поля в этой точке. линии поля чертятся так, чтобы их густота, т. е. число линий, проходящих через единицу площади, давала модуль магнитной индукции магнитного поля. Таким образом, мы будем получать «магнитные карты», способ построения и употребления которых аналогичен «электрическим картам» Главное отличие магнитного поля то, что линии его всегда оказываются замкнутыми. построение линий магнитного поля 8 Магнитный момент контура с токомМагнитный момент – величина, характеризующая магнитные свойства вещества. - результирующая сила действующая на виток с током в постоянном магнитном поле. Если поле однородно, то В – постоянная выносится из под интеграла , а = 0 плоский виток, плоскость которого параллельна магнитному полю В , где - высота , - момент сил, образуемый силами F1 и F2. - плечо пары,- площадь четырехугольника. , S – площадь, охватываемая рассматриваемым витком тока в векторной форме , магнитный момент тока ( если вектор S направлен перпендикулярно плоскости рисунка и направлен к нам) 9 - вращающий момент Под действием вращающего момента М виток или катушка будут поворачиваться так, чтобы векторы М и В стали параллельными и одинаково направленными. Это — положение устойчивого равновесия. Когда размеры витка или катушки малы влиянием неоднородности поля на вращающий момент можно пренебречь. Катушки, используемый для практического измерения магнитных полей – пробные. Если пробную катушку поместить в магнитное поле, то ее магнитный момент установится вдоль поля . Повернем катушку из этого положения на 90°, чтобы вращающий момент М обратился в максимум. Тогда магнитный момент перпендикулярен к В.
Измерив вращающий момент М, можно по этой формуле найти напряженность магнитного поля как по модулю, так и по направлению. В частности, такие измерения позволяют проверить закон Био и Савара в интегральной форме 10 Потенциальная энергия магнитного момента в магнитном поле
11 Сила, действующая на магнитный момент.Элементарный контур – плоский контур маленького размера. Его поведение легко описывать с помощью магнитного момента легче описывать. 1) в однородном магнитном поле так как 2) направление | | элементарному приращению В, взятого в направлении.
Момент сил. studfiles.net 4.4. Магнитное поле кругового токаРассмотрим проводник с током, имеющий форму окружности радиуса R (рис.4.5 ). Определим магнитную индукцию в его центре. Каждый элемент тока создает магнитное поле индукцией, перпендикулярное к плоскости витка. . (4.19) Все векторанаправлены одинаково, поэтому их векторное сложение сведется к сложению их модулей. Тогда . Так как , то для магнитной индукции в центре кругового тока получаем: . (4.20) Определим магнитную индукцию в любой точке на оси кругового тока. Обозначимx расстояние от плоскости контура до некоторой точки на оси (рис.4.6). Так как вектор , то модуль вектораравен: . (4.21) Вектор перпендикулярен плоскостям, проходящим черези(рис.4.6). От всех элементов тока будет образовываться «конус» векторов. Разложим вектор на две составляющие: перпендикулярную и параллельную оси:. Применим принцип суперпозиции полей, получим:
Нетрудно убедиться, что векторная сумма всех перпендикулярных составляющих равна нулю, и результирующий вектор будет направлен вдоль оси тока. Вклад в него будут вносить только параллельные оси составляющие векторов. Тогда . (4.22) Из треугольника (см. рис.4.6) следует: . (4.23) Подставим выражение (4.21) в формулу (4.23), получим: . (4.24) Возьмём интеграл: , получим: , или . (4.25) Так как , то окончательно получим: . (4.26) При x=0 формула (4.26) переходит в (4.20). 4.5. Магнитный момент витка с токомРассмотрим замкнутый контур с током (рис. 4.7). Обозначим - единичный вектор положительной нормали к контуру. Этот вектор связан с направлением тока правилом правого винта. Магнитным моментом контура с током называется вектор , равный . (4.27) Здесь S - площадь, охватываемая контуром. Если контур круговой, то , тогда . (4.28) Для магнитной индукции на оси кругового тока было получено выражение: . (4.29) Во многих случаях приходиться иметь дело с замкнутыми токами, размеры которых малы по сравнению с расстояниями до точки наблюдения. Такие токи принято называть элементарными. (Пример: движущийся по замкнутой орбите электрон). На больших расстояниях от контура x>>R и можно пренебречь вторым слагаемым в знаменателе, тогда . (4.30) Умножим числитель и знаменатель этого выражения на π, получим: , (4.31) где . Произведение силы тока на площадь контура равно по величине магнитному моменту контура. Так как векторы инаправлены одинаково, то . (4.32) Индукция магнитного поля, созданного элементарным током, пропорциональна его магнитному моменту. studfiles.net Круговой ток - Большая Энциклопедия Нефти и Газа, статья, страница 1Круговой токCтраница 1 Круговые токи в них возникают ( индуцируются) лишь при возбуждении внешним магнитным полем. XVIII мы увидим, что направление этих индуцированных токов таково, что создаваемое ими магнитное псле направлено против внешнего магнитного поля. Этим объясняется уменьшение суммарной напряженности магнитного поля в диамагнитной среде. [1] Эти круговые токи на горизонте черной дыры аналогичны вихревым токам, которые возбуждаются в проводящей металлической сфере, вращающейся в наклонном магнитном поле. [3] Система одинаковых круговых токов с общей прямолинейной осью называется соленоидом. [5] Это подразумевает более низкий круговой ток и, следовательно, более низкий магнитный момент. [6] В центре кругового тока с радиусом 5 8 см индукция магнитного поля равна 1 3 - 10 - 4 тл. [7] Магнитное поле кругового тока ( см. рис. 14.4, в), представляющего собой один виток соленоида, подобно полю очень короткого полосового магнита, расположенного в центре витка так, что его ось перпендикулярна плоскости витка. [8] В центре кругового тока с радиусом 5 8 см индукция магнитного поля равна 1 3 10 - 4 тл. [9] В центре кругового тока с радиусом 5 8 см индукция магнитного поля равна 1 3 - 10 - Тл. [10] В центре кругового тока с радиусом 5 8 см индукция магнитного поля равна 1 3 - 10 - 4 Тл. [11] Однако поле кругового тока, или поле одного витка, является очень слабым. Для создания более сильного поля ток пропускают через проводник, согнутый в виде спирали, называемой соленоидом. У соленоида поля отдельных витков складываются и дают сильное результирующее поле. [12] Магнитное поле кругового тока показано на рис. 22.6. Направление линий индукции магнитного поля видно по положению магнитной стрелки. Оно определяется с помощью правила правого винта. [13] Ампера об элементарных электрических круговых токах, текущих и в северном и в южном концах магнита в одном и том же направлении, служит моделью этого движения. Мы видим, что истинная симметрия магнита не дает ни малейшего повода называть зеркально равные концы магнита полюсами. Полюсов в принятом значении этого слова у магнита нет; силовые магнитные линии не полярны, а аксиальны. Если же мы хотим продолжать пользоваться привычным термином, следует говорить о полярных и аксиальных полюсах. [14] Страницы: 1 2 3 4 www.ngpedia.ru Магнитное поле - круговой токМагнитное поле - круговой токCтраница 1 Магнитное поле кругового тока ( см. рис. 14.4, в), представляющего собой один виток соленоида, подобно полю очень короткого полосового магнита, расположенного в центре витка так, что его ось перпендикулярна плоскости витка. [1] Магнитное поле кругового тока показано на рис. 22.6. Направление линий индукции магнитного поля видно по положению магнитной стрелки. Оно определяется с помощью правила правого винта. [2] Но магнитное поле кругового тока / эквивалентно, как известно, полю магнитного диполя с моментом MsAf / c, где А - площадь, охватываемая током, и с - скорость света. [3] Определим напряженность магнитного поля кругового тока. [4] На рис. 227 представлена картина магнитного поля кругового тока. [6] Он имеет направление, как и у вектора индукции магнитного поля кругового тока, перпендикулярное к плоскости витка и определяемое правилом буравчика. [7] На рис. 118 приведены полученные таким способом картины линий индукции магнитного поля кругового тока и поля соленоида. [9] Магнитный момент - величина векторная, совпадает по направлению с вектором индукции магнитного поля кругового тока. [10] Выполнив данную работу, можно убедиться, что картина вихревого электрического поля, созданного переменным магнитным потоком тороида, аналогична магнитному полю кругового тока или короткого соленоида. [11] Магнитное поле в центре атома создается как орбитальным, так и спиновым магнитным моментом электронов. Так как природа этих моментов не одинакова, соотношение между направлением поля и направлением магнитных моментов различно. Для одноэлектронного атома это грубо проиллюстрировано на рис. 16.3. Магнитное поле орбитального момента можно рассматривать как магнитное поле кругового тока; оно параллельно орбитальному магнитному моменту. Магнитное поле, созданное спиновым моментом, следует рассматривать как поле точечного диполя, расположенного на орбите. [12] Страницы: 1 www.ngpedia.ru Круговой ток - Большая Энциклопедия Нефти и Газа, статья, страница 2Круговой токCтраница 2 На рисунке изображены круговой ток и расположенная на его оси компасная стрелка. [16] На рисгнке изображены круговой ток в расположенная на его. [17] Магнитное поле и сверхпроводящие круговые токи показаны только для двух вихревых нитей. Тонкой линией показан один из элементов треугольной структуры. [18] Остается найти поле кругового тока на его оси. [19] Точный расчет индуктивности кругового тока с помощью эллиптических интегралов довольно сложен. [20] Так как поле кругового тока нетрудно вычислить, зная ток, то горизонтальную составляющую земного магнитного поля можно определить по углу отклонения стрелки и величине поля тока. [21] Но магнитное поле кругового тока / эквивалентно, как известно, полю магнитного диполя с моментом MsAf / c, где А - площадь, охватываемая током, и с - скорость света. [22] Остается найти поле кругового тока на его оси. [23] Возникающие в подвижной системе круговые токи несимметричны по отношению к оси вращения и, взаимодействуя с потоками, создают вращающий момент. [24] В этом случае получатся круговые токи, которые в результате изменений, вызываемых колебаниями, создают переменное магнитное поле, индукционное действие которого на неподвижную катушку можно вычислить точно так же, как на странице 317 было вычислено действие переменного тока, получаемого обычным способом. [25] Положим, что имеем круговой ток силы / с радиусом R. В этом случае все элементы тока перпендикулярны к радиусам-векторам р и поэтому в формуле (87.2) sin &1. Далее, из рис. 162 видно, что магнитные поля dfft и dtf %, создаваемые какой-либо парой элементов тока / и 2, расположенных на одном диаметре, складываясь, дают поле dH, направленное вдоль оси тока. Поэтому и полное поле всего кругового тока направлено по его оси. [27] Иногда за магнитный момент кругового тока принимают величину рт ( Xo / S, где ( АО - магнитная постоянная. Оба эти определения в одинаковой мере возможны. [28] Определим напряженность магнитного поля кругового тока. [29] Иногда за магнитный момент кругового тока принимают величину рт fjio / S, где fjio - магнитная постоянная. Оба эти определения в одинаковой мере возможны. [30] Страницы: 1 2 3 4 www.ngpedia.ru |
|
||||||||||||||||||
|
|
||||||||||||||||||
|




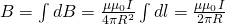




 — Магнитная индукция прямого тока
— Магнитная индукция прямого тока — Магнитная постоянная
— Магнитная постоянная — Магнитная проницаемость среды
— Магнитная проницаемость среды — Сила тока
— Сила тока — Расстояние от провода до точки, где мы вычисляем магнитную индукцию
— Расстояние от провода до точки, где мы вычисляем магнитную индукцию — Угол между вектором dl и r
— Угол между вектором dl и r









