Косинус фи формула: Коэффициент мощности

Содержание

Косинус фи — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Косинус фи ( cos:; — косинус угла сдвига фаз между током и напряжением в цепи переменного тока.
[1]

Косинус фи ( cos ф) — косинус угла сдвига фаз между напряжением и током в цепи переменного тока. От него зависит мощи ость ( ом.
[2]

Коэффициент мощности ( косинус фи) для осветительной или, как говорят, чисто активной нагрузки близок к единице. Для остальной производственной ( двигательной) нагрузки он существенно меньше единицы.
[3]

При переменном токе мощность в некоторые периоды времени отрицательна, т. е. электрическая энергия частично возвращается от потребителя к источнику тока. Источник тока отдает одновременно.
[4]

Величину cos ф ( косинус фи) называют коэффициентом мощности; по значению cos ф можно судить о том, как использует мощность источника тока данная электрическая цепь или электрическая установка.
[5]

На графике изображают изменение косинуса фи через каждый час. Сложив все величины часового расхода электроэнергии, активной и реактивной, и поделив суточный расход реактивной энергии на суточный расход активной энергии, получают тангенс фи, а по нему — средневзвешенный косинус фи предприятия за сутки.
[6]

Коэффициентом мощности, или косинусом фи ( cos ф), цепи называется отношение активной мощности к полной мощности.
[7]

Коэффициентом мощности, или косинусом фи ( соз ф), цепи называется отношение активной мощности к полней мощности.
[8]

Существует ряд способов для повышения косинуса фи; однако их рассмотрение выходит за рамки нашей книги.
[9]

Если установленное ( регламентированное значение косинуса фи поддерживается или повышается в установленных пределах, предприятие получает премию или дополнительную скидку с тарифа.
[10]

Необходимо указать на условность понятия средневзвешенного косинуса фи и ограниченную область его применения.
[11]

Как видно, коэффициент мощности ( косинус фи) служит важным показателем степени использования кажущейся мощности, развиваемой генератором переменного тока. Надо обратить особое внимание на то, что при cos5 1 генератор должен создавать напряжение и ток, произведение которых больше величины активной мощности.
[12]

Трансформаторы-высокой частоты и их изображение на схемах.
[13]

В трансформаторах малой и средней мощности косинус фи бывает ниже и не играет такой большой роли. Эти трансформаторы обычно характеризуют только величиной активной мощности.
[14]

В этой формуле cos ф ( косинус фи) — коэффициент мощности, который характеризует сдвиг фаз в цепи. Этот коэффициент обычно бывает меньше единицы.
[15]

Страницы:

Чем отличаются кВа и кВт?

Вольт-ампер (ВА или VA) – единица, используемая для обозначения полной мощности переменного тока, определяемая как произведение силы тока действующей в цепи (измеряется в амперах, сокращенно A) и напряжения на зажимах цепи (измеряется в вольтах, сокращенно B).

Ватт (Вт или W) – единица , применяемая для измерения мощности. Своим названием данная единица обязана шотландско-ирландскому изобретателю Джеймсу Уатту. 1 ватт – мощность, при которой за время равное 1с. совершается работа в 1Дж. Ватт является единицей активной мощности, значит, 1 ватт – мощность постоянного электрического тока силой 1A при напряжении равном 1B.

!Выбирая дизель генератор нужно помнить о том, что полная мощность, потребляемая прибором, измеряется в кВА, а активная мощность, затрачиваемая на то, чтобы совершить полезную работу измеряется в кВт. Полная мощность рассчитывается как сумма двух слагаемых реактивной мощности и активной мощности. Весьма часто отношение полной и активной мощностей имеет различные значения для разных потребителей, поэтому, для того, чтобы найти суммарную мощность всего потребляющего оборудования требуется провести суммирование полных, а не активных мощностей оборудования.

Номинальная мощность

Мощность большинства промышленных электроприборов определяется в ваттах, это активная мощность, выделяющаяся на резистивной нагрузке (лампочка, нагревательные приборы, холодильник и т. п.).

Обычно под потребляемой мощностью понимают именно активную мощность, полностью идущую на полезную работу. В случае, если речь идет об активном потребителе (чайник, лампа накаливания), то на нем, как правило, написаны номинальное напряжение и номинальная мощность в Вт, этой информации достаточно, чтобы вычислить косинус «фи».

Угол «фи» – это угол между напряжением и током. Для активных потребителей угол «фи» равен 0, а, как известно, cos(0) = 1. Для того, чтобы вычислить активную мощность (обозначается P) нужно найти произведение трех множителей: тока через потребитель, напряжения на потребителе, косинуса «фи», то есть провести расчёты по формуле

P=I×U×сos(φ)= I×U×cos(0)=I×U

Рассмотрим пример для ТЭНа. Так как это активный потребитель, то cos(0) = 1. Полная мощность (обозначаемая S) будет равна 10кВА. Следовательно, P=10× cos(0)=10 кВт — активная мощность.

Если же речь идет о потребителях, имеющих не только активное, но и реактивное сопротивление, то на них, как правило, указывается P в Вт (активная мощность) и величина косинуса «фи».

Приведем пример для двигателя, на бирке которого написано: P=5 кВт, сos(φ)=0.8, отсюда следует, что этот двигатель, работая в номинальном режиме будет потреблять S = P/сos(φ)=5/0,8= 6,25 кВа — полная (активная) мощность и Q = (U×I)/sin(φ) — реактивная мощность.

Чтобы найти номинальный ток двигателя необходимо разделить его полную мощность S на рабочее напряжение равное 220 B.

Однако номинальный ток можно также прочитать на бирке.

Почему мощность на генераторах указывается в ВА?

Ответ следующий: пусть мощность стабилизатора напряжения, указанная на бирке равна 10000 ВА, если к этому трансформатору подключить некоторое количество ТЭНов, то отдаваемая трансформатором мощность (трансформатор работает в номинальном режиме) не превысит 10000 Вт.

В данном примере все сходится. Однако, если же подключить к стабилизатору напряжения катушку индуктивности (много катушек) или электродвигатель со значением сos(φ)=0.8. В итоге мощность отдаваемая стабилизатором будет равна 8000 Вт. Если же для электродвигателя сos(ф)=0.85, то отдаваемая мощность будет равна 8500 Вт. Отсюда следует, что надпись 10000Ва на бирке трансформатора не будет соответствовать действительности. Именно поэтому, мощность генераторов (стабилизаторов и трансформаторов напряжения) определяется в полной мощности (для рассмотренного примера 1000 кВА).

Коэффициент мощности рассчитывается как соотношение средней мощности переменного тока и произведения действующих в цепи значений тока и напряжения. Максимальное значение,которое может принимать коэффициент мощности равно 1.

При рассмотрении синусоидального переменного тока, для определения коэффициента мощности используется формула:

сos(φ) = r/Z

r и Z – соответственно активное и полное сопротивления цепи, а угол φ– это разность фаз напряжения и тока. Отметим, что коэффициент мощности может принимать значения меньшие 1, даже в цепях с только активным сопротивлением, если в них присутствуют нелинейные участки, так как происходит изменение формы кривых тока и напряжения.

Коэффициент мощности равен также косинусу угла фаз между основаниями кривых тока и напряжения. Коэффициент мощности – отношение активной мощности к полной мощности: сos(φ) = активная мощность/полная мощность = P/S (Вт/ВА). Коэффициент мощности – это комплексная характеристика нелинейных и линейных искажений, которые вносятся в сеть нагрузкой.

Значения, принимаемые коэффициентом мощности:

1.00 – очень хороший показатель;
0.95 — хорошее значение;
0.90 — удовлетворительное значение;
0.80 — среднее значение;
0.70 — низкое значение;
0.60 — плохое значение.

Вам может быть интересно

Зачем нужен бензогенератор со сварочным аппаратом
Где купить мощный компрессор для производства
Как устроен бензогенератор для инверторной сварки
Чем генератор Элемакс отличается от электростанции SDMO

3.

8 Фи-функция Эйлера

Когда что-то известно о $\Z_n$, часто полезно спросить
применимо ли что-то сопоставимое к $\U_n$. Здесь мы смотрим на $\U_n$
в контексте предыдущего раздела. В помощь расследованию мы
ввести новую величину, фи-функцию Эйлера , записанную
$\phi (n)$, для натуральных чисел $n$.

Определение 3.8.1 $\phi (n)$ — это количество
неотрицательные целые числа меньше $n$, относительно
просто до $n$.
Другими словами, если $n>1$, то $\phi (n)$ — это количество
элементы в $\U_n$ и $\phi(1)=1$.
$\квадрат$

Пример 3.8.2. Легко проверить, что $\phi (2)=1$, $\phi (4)=2$, $\phi
(12)=4$ и $\phi (15)=8$.
$\квадрат$

Пример 3.8.3. Если $p$ — простое число, то $\phi (p)=p-1$, поскольку
$1$, $2$, …, $p-1$ взаимно просты с $p$, а $0$ — нет.
$\квадрат$

Для любого числа $n$ $\phi(n)$ оказывается удивительно простым
форма; то есть существует простая формула, которая дает значение
$\фи(п)$. Мы уже видели, насколько это просто для простых чисел. Как есть
типичных для многих результатов в теории чисел, мы будем работать по-своему
постепенно до любого $n$, глядя затем на степени одного простого числа.
9{a-1}$.$\qed$

Пример 3.8.5 $\phi (32)=32-16=16$, $\phi (125)=125-25=100$.
$\квадрат$

Теперь мы хотим расширить нашу формулу, чтобы обрабатывать любые
натуральное число $n$.
Сначала рассмотрим пример:

Пример 3.8.6
С
$$
\eqalign{ \U_{20}&=\{[1],[3],[7],[9],[11],[13],[17],
[19]\},\кр
\U_{4}& =\{[1],[3]\},\cr
\U_{5}& =\{[1],[2],[3],[4]\},\cr}
$$
и $\U_{20}$, и $\U_4\times \U_5$ имеют по 8 элементов. Фактически,
переписка, обсуждаемая в китайском остатке
Теорема между $\Z_{20}$ и
$\Z_{4}\times \Z_5$ также является соответствием 1-1 между $\U_{20}$ и
$\U_4\раз \U_5$:
$$
\матрица{
[1]&\стрелка влево&([1],[1])&\quad&[11]&\стрелка влево& ([3],[1])\cr
[3]&\стрелка влево&([3],[3])&\quad&[13]&\стрелка влево& ([1],[3])\cr
[7]&\стрелка влево&([3],[2])&\quad&[17]&\стрелка влево& ([1],[2])\cr
[9]&\стрелка влево&([1],[4])&\quad&[19]&\стрелка влево& ([3],[4])\cr}
$$
$\квадрат$

Использование китайского остатка
Теорема, мы можем доказать, что это
правда в общем.

Теорема 3.8.7.
Если $a$ и $b$ относительно
простое и $n=ab$, то
$\phi (n)=\phi (a)\phi (b)$.

Доказательство.
Мы хотим доказать, что $|\U_n|=|\U_a|\cdot|\U_b|$. Как указано
в примере мы на самом деле докажем больше, выставив единицу за
одно соответствие между элементами $\U_n$ и
$\U_a\раз\U_b$. У нас уже есть переписка один на один между
элементы $\Z_n$ и $\Z_a\times\Z_b$. Опять же, как указывает
например, нам просто нужно доказать, что это же соответствие работает для
$\U_n$ и $\U_a\times\U_b$. То есть мы уже умеем связывать
любой $[x]$ с парой $([x],[x])$; нам просто нужно знать, что $[x]\in
\U_n$ тогда и только тогда, когда $([x],[x])\in\U_a\times\U_b$. После долгого
построить, вот доказательство: $[x]$ находится в $\U_n$ тогда и только тогда, когда
$(х,n)=1$
тогда и только тогда, когда $(x,a)=1$ и $(x,b)=1$ тогда и только тогда, когда $([x],[x])\in
\U_a\times \U_b$.$\qed$

Следствие 3.8.8. Предположим, что $n=ab$, где $a$ и $b$ взаимно просты.
Для $x=0,1,…, n-1$, если $[x]\in \U_{n}$, свяжите $[x]$ с
$([x], [x])\in \Z_a\times \Z_b$. Это дает один к одному
соответствие между $\U_n$ и $\U_a\times \U_b$.

Доказательство.
Мы доказали это уже в доказательстве предыдущего
теорема, но она заслуживает отдельного утверждения.$\qed$

Теперь мы знаем достаточно, чтобы вычислить $\phi(n)$ для любого $n$.

Пример 3.8.9 $\phi (200)=\phi(25)\phi(8)=(25-5)(8-4)=80.$
$\квадрат$
9{e_k-1}).
$$

Доказательство.
Доказательство по индукции оставляем в качестве упражнения.$\qed$

Леонард Эйлер. Эйлер родился в Базеле.
в 1707 году и умер в 1783 году, после потрясающе плодовитой жизни.
математическая работа. Его полная библиография насчитывает около 900
записи; его исследования составили около 800 страниц в год в течение всего
его карьеры. Он продолжал заниматься исследованиями вплоть до своего внезапного
смерть во время отдыха с чашкой чая. Почти все последние 17
лет своей жизни он был полностью слеп.

Широта знаний Эйлера может быть столь же впечатляющей, как и глубина его
его математическая работа. У него были большие способности к языкам, и
изучал теологию, медицину, астрономию и физику. Его первый
назначение было в медицине при недавно созданном Санкт-Петербургском
Академия. В день приезда в Россию покровитель академии,
Екатерина I умерла, а сама академия едва пережила
переход власти к новому режиму. В результате Эйлер оказался в
кафедра натурфилософии вместо медицины.

Эйлера лучше всего помнят за его вклад в анализ и числа.
теории, особенно за использование им бесконечных процессов различных
виды (бесконечные суммы и произведения, цепные дроби), а для
установив большую часть современной нотации математики. Эйлер
положил начало использованию $e$ для основания натуральных логарифмов и $i$
для $\sqrt{-1}$; символ $\pi$ был найден в книге, изданной
в 1706 г., но принятие этого символа Эйлером в 1737 г. сделало
это стандарт. Он также отвечал за использование $\sum$ для
представляют собой сумму, а в современных обозначениях функции $f(x)$.
92/6$.
Некритическое применение Эйлером обычной алгебры к бесконечным рядам
время от времени приводил его к неприятностям, но его результаты были в подавляющем большинстве
правильны, а позже были оправданы более тщательной техникой, поскольку
потребность в повышенной строгости математических аргументов стала очевидной.
Мы еще не раз встретимся с именем Эйлера в оставшейся части главы.

Информация здесь взята из История математики , автор
Карл Бойер, Нью-Йорк: John Wiley & Sons, 1968.

9{-1}$ соответствуют?

Пример 3.8.5
Делителями числа $6$ являются $1$, $2$, $3$, $6$. Обратите внимание, что
$$
\фи (1)+\фи (2)+\фи (3)+\фи (6)= 1 + 1 + 2 + 2 = 6.
$$
Выполните аналогичные вычисления, заменив 6$ на 10$.

Пример 3.8.6
Найдите все $a$ такие, что $\phi (a)=6$.

Пример 3.8.7
Если $a|b$, докажите $\phi (a)|\phi (b)$.

Пример 3.8.8
Какие простые числа можно представить в виде $\phi (n)$ для
какие-то $n$?

Пример 3.8.9
Докажи это
$\displaystyle\phi(n)=n\prod_{p|n}\big(1-{1\over p}\big)$; продукт
над всеми простыми числами $p$, которые делят $n$.

Пример 3.8.10
Докажите теорему 3.8.11.

Пример 3.8.11
Найдите все $n$, для которых $\phi(n)$ нечетно, и докажите
что вы нашли все такие $n$.

Пример 3.8.12
В доказательстве теоремы 3.8.7
мы утверждали, что если $n=ab$, то $(x,n)=1$
тогда и только тогда, когда $(x,a)=1$ и $(x,b)=1$. Докажите это.

Измерение коэффициента мощности методом трех вольтметров

Введение

Измерение коэффициента мощности (также называемого cos φ )
что нам часто приходится делать при работе с сетевыми цепями переменного тока.
В идеале каждая нагрузка, подключенная к сети, должна иметь
cos(φ) из 1, но многие устройства, такие как электродвигатели или старые
балласты люминесцентных ламп являются индуктивными и имеют более низкий коэффициент мощности.
Для корректировки коэффициента мощности обычно используется конденсатор подходящего номинала.
подключены параллельно.
Но чтобы убедиться, что конденсатор эффективно корректирует коэффициент мощности,
нет другого способа, кроме как измерить его.

Надо сказать, что обратная ситуация, пусть и не очень частая, бывает.
также возможно: нагрузка переменного тока может иметь низкий коэффициент мощности из-за
емкость, которую можно исправить, добавив катушку индуктивности.
Опять же, измерение коэффициента мощности — единственный способ убедиться, что мы все сделали правильно.
работа.

Несколько слов о коэффициенте мощности

Если вы читаете эту страницу, я предполагаю, что вам нужно измерить
коэффициент мощности, а в данном случае вы уже знаете, что это такое.
Если нет, я попытаюсь кратко объяснить это здесь.

В цепи постоянного тока мощность, рассеиваемая нагрузкой, равна ее току I
умножить на напряжение U на его клеммах: P =
У·И .
Для цепей с питанием от переменного тока все немного сложнее: напряжение и ток меняются.
со временем и сила тоже.
Другими словами, мгновенная мощность всегда является произведением
мгновенное напряжение и мгновенный ток, поэтому мы имеем
p(t) = u(t)·i(t) .
Но это нецелесообразно, так как мгновенная мощность p(t) изменяется
со временем: иметь сравнимую «постоянную» мощность P как у нас
используется в постоянном токе, p(t) усредняется по полному циклу переменного тока.

Теперь, в зависимости от фактической природы u(t) и i(t) ,
результирующая мощность P может отличаться.
Ограничимся линейными цепями (состоящими только из резисторов,
катушки индуктивности и конденсаторы) и синусоидальные сигналы, как обычно в цепях переменного тока,
так что мы можем использовать некоторые ярлыки и упростить математику.
Здесь для расчета (активной) мощности уравнение немного сложнее:
P = U·I·cos(φ) , где cos(φ) –
коэффициент мощности, а φ — фазовый угол между напряжением и током.

Просто умножая напряжение на ток, как мы привыкли делать в постоянном токе
схема дает полную мощность S = U·I .
Оно называется кажущимся, потому что не соответствует полезной мощности, которую
нагрузку можно использовать, она как раз получается путем умножения U и I .
Чтобы подчеркнуть разницу между активной мощностью P и полная мощность
S , первое измеряется в ваттах (Вт), а второе измеряется в
Вольт-Ампер (ВА), напомнив, как он был рассчитан.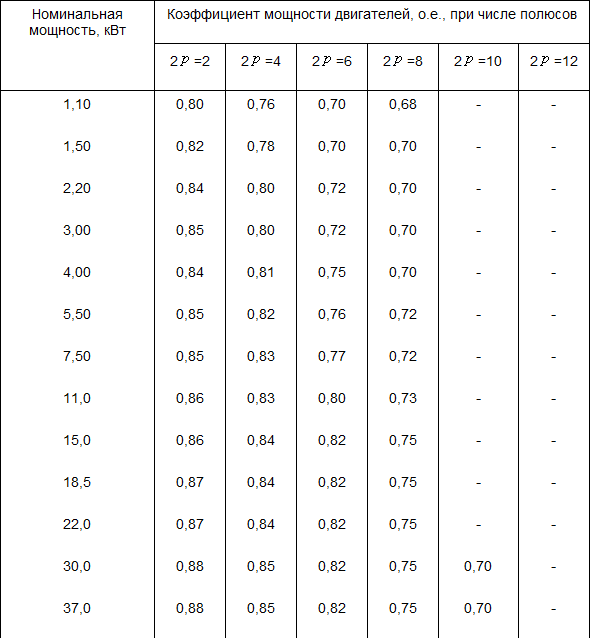

Например, если нагрузка представляет собой чистый резистор, напряжение и ток
точно в фазе, φ = 0° , cos(φ) = 1
и мы можем просто вычислить P = U·I , как мы привыкли делать
с цепями постоянного тока.
Такими должны быть все нагрузки, подключенные к сети.

Если нагрузкой является идеальный конденсатор, ток всегда опережает напряжение на
φ = –90° и cos(φ) = 0 : это означает
мощность, усредненная за один полный цикл, равна нулю.
Это нормально, потому что конденсаторы не рассеивают мощность.
Но теперь у нас есть P = 0 , даже если U и I оба
ненулевой.
Здесь термин «кажущаяся» мощность заслуживает всего своего значения: она выглядит
как если бы мощность подавалась на нагрузку, S = U·I не является
ноль, но из-за разности фаз (коэффициента мощности) P равен нулю!
То же самое верно для идеального индуктора, где φ = +90° ,
но cos(φ) = 0 и P = 0 , как и раньше.

Реальные нагрузки никогда не бывают идеальными катушками индуктивности или конденсаторами, а представляют собой смесь сопротивлений.
с емкостью или индуктивностью.
В любом случае φ находится между –90° и +90°, а
cos(φ) всегда находится между 0 и 1.
Стоит отметить, что коэффициент мощности cos(φ) всегда
между 0 и 1, независимо от того, является ли угол φ отрицательным (емкостная
нагрузка) или положительная (индуктивная нагрузка).

Обратите внимание, что для вычисления мощности необходимо выразить U и I .
в их среднеквадратичном значении, а не в их пиковом значении.

Метод трех вольтметров

Измерители коэффициента мощности существуют, но их трудно найти и почти никогда не используют.
доступны на верстаке домашнего пивовара.
Даже если у вас есть осциллограф, это все еще сложное измерение:
осциллографы имеют внутреннее заземление и не могут быть напрямую подключены к
сеть переменного тока; плавающий осциллограф с разделительным трансформатором
опасная эксплуатация, так как шасси прицела будет находиться под потенциалом сети.
Тогда большинство осциллографов не выдерживают прямого сетевого питания.
напряжения на их входах и требуются специальные высоковольтные щупы.
С другой стороны, если все эти проблемы можно решить, измерив угол
φ на осциллографе очень точно.

К счастью, есть очень простой прием для измерения cos(φ) , который называется
метод трех вольтметров : вам просто нужны три вольтметра переменного тока и
резистор.
Но на практике трех вольтметров особо и не нужно: можно обойтись и
только один, и очень часто лучше использовать только один.

Недостатком является то, что он отлично работает только для линейных нагрузок, таких как двигатели или
трансформаторы; он также неплохо работает с некоторыми слегка нелинейными нагрузками, такими как
индуктивные балласты люминесцентных ламп или трансформаторные дуговые сварочные аппараты, но
не работает с сильно нелинейными нагрузками, такими как выпрямители (практически любые
электронный балласт, импульсный источник питания, двигатель с частотным приводом
преобразователи. ..).

Идея проста: достаточно подключить резистор R последовательно с нагрузкой
и измерьте три напряжения U ₁ , U ₂ и
U ₃ как показано на этой схеме:

Соединения трех вольтметров и дополнительного резистора.

После измерения трех напряжений U ₁ ,
U ₂ и U ₃ просто используйте следующие
уравнение для прямого расчета коэффициента мощности:

Фактическое значение R не требуется для расчета мощности
Фактор, падение напряжения U ₂ на нем — это все, что вам нужно.

Практические замечания

Правильный выбор резистора имеет решающее значение.
Чтобы узнать лучшее значение R , вы должны сбалансировать два аспекта:
точность и падение напряжения.
Вам нужен резистор, достаточно большой, чтобы ваш вольтметр (или мультиметр) мог
измерить его с достаточной точностью; но не слишком большой, иначе напряжение
доступных для нагрузки будет слишком мало.

Напряжение сети питания обычно гарантировано в пределах ±5%.
от своего номинала (а иногда даже ±10%): потеря нескольких вольт
через R часто не проблема.
И многие мультиметры имеют тенденцию быть довольно неточными при измерении малых переменных величин переменного тока.
напряжения (по крайней мере, дешевые), поэтому, я думаю, от 5 до 10 В на этом
резистор разумный.

Резистор должен выдерживать мощность ( P =
U ₂ ² /R ) без перегрева, по крайней мере, для всех
время, необходимое для выполнения измерений, поэтому используйте деталь с соответствующей номинальной номинальной мощностью.

Вы также хотите резистор, который не является индуктивным, но это обычно не
проблема на частоте 50 или 60 Гц, где индуктивность, например, 100 мкГн, часто может
пренебрегать.

Мощные резисторы могут быть дорогими или их трудно найти, но этот метод
не требует точного значения R : проявив немного творчества, вы можете
возможно, вы найдете подходящую деталь в своем мусорном ящике.
Например, лампочка накаливания может быть решением: она не индуктивная и
некоторые модели могут выдерживать большую мощность.
Лампочки представляют собой нелинейные резисторы, так как их номинал меняется в зависимости от тока.
но если ваша нагрузка стабильна, их можно использовать.
Другими примерами являются резистивные нагревательные элементы, такие как электрические водогрейные котлы.
чайники, тостеры,… все они имеют мощные резисторы внутри, может быть, вы
может найти то, что вам нужно на вашей кухне.

Теперь несколько слов об использовании трех вольтметров одновременно или только одного.
и измерьте три напряжения одно за другим.
Позже мы увидим, что этот метод определяет угол, измеряя три
стороны треугольника, две очень длинные стороны ( U ₁ и
U ₃ ) и очень короткий ( U ₂ ).
Если одно или два измерения неверны, это приведет к значительным
ошибка в ракурсе.
С другой стороны, если все измерения отличаются на один и тот же процент, все
ошибки компенсируются, и угол будет правильным.
Итак, если у вас нет трех точных и хорошо откалиброванных инструментов, это намного
лучше использовать один и тот же для измерения трех напряжений.
Проверьте свои инструменты перед проведением измерений, это сэкономит вам
много времени!

Пять мультиметров, измеряющих напряжение сети: не все они совпадают
такое же значение.
Это хорошая идея, чтобы проверить ваши инструменты в первую очередь. (нажмите, чтобы увеличить).

Но использование только одного вольтметра имеет некоторые недостатки: во-первых, напряжение сети
часто неустойчивы.
Если он изменится во время измерения, это приведет к ошибкам.
Для этого можно попробовать проводить измерения ночью, когда меньше
вариации.
Контроль сетевого напряжения с помощью дополнительного прибора (даже если он не
точно) может быть хорошей идеей: он покажет вам, насколько стабильно напряжение, и
если вы видите, что он слишком сильно меняется, просто повторите все три измерения (в конце концов
это не займет много времени).

Во-вторых, если ваша нагрузка непостоянна, а меняется со временем, у вас будет
тяжелое время только с одним вольтметром.
В этом случае вам понадобятся три хороших и откалиброванных мультиметра, но если вы
у вас их еще нет, вероятно, дешевле купить измеритель коэффициента мощности …

Калькулятор коэффициента мощности

Следующий калькулятор рассчитает за вас: просто введите три
напряжения У ₁ , У ₂ и У ₃ ,
и нажмите кнопку «Вычислить», чтобы найти cos φ .

Если вы также введете значение сопротивления R (опционально), это
калькулятор рассчитает ток линии I полная мощность S
а активная мощность P .

(*): Необязательное значение.

Как это работает

Окончательная формула выглядит очень просто, и вам может быть интересно, почему это работает.
Итак, давайте еще раз рассмотрим схему:

Принципиальная схема цепи. Подчеркнутые буквы — вектора.

Векторная сумма U ₂ и U ₃
конечно U ₁ , а поскольку R — чистый резистор,
ток I точно совпадает по фазе с напряжением
U ₂ , как показано на векторной диаграмме ниже:

Векторная диаграмма трех напряжений U ₁ ,
U ₂ и U ₃ и их
отношение с углами α и φ .

Искомый угол равен φ , между током нагрузки
I и напряжение нагрузки U ₃ , при этом
α — угол между U ₂ и
У ₃ .
Используя закон косинусов и учитывая только величины фазоров,
мы можем написать:

Это просто отношение между тремя сторонами U ₁ ,
U ₂ и U ₃ треугольника и угла
α .

Теперь мы можем немного перестроиться и найти cos(α) :

Из нашей векторной диаграммы выше мы имеем следующее:

Подставляя и используя свойство cos(180° – x) =
–cos(x) , теперь мы можем найти cos(φ) :

И, наконец, мы имеем:

В приведенном выше калькуляторе, если задано значение R , ток нагрузки
рассчитывается с:

Что позволяет рассчитать полную мощность с помощью:

А так как мы только что нашли коэффициент мощности cos(φ) , то и активный
мощность можно легко рассчитать с помощью:

Несколько примеров

Чтобы лучше проиллюстрировать этот метод, давайте рассмотрим несколько примеров.
Даже если я обычно использую только один мультиметр, потому что у меня нет трех хороших
качественные надежные мультиметры, а потому с помощью одного и того же прибора три
раз точнее, здесь я позаимствовал некоторые верные инструменты, чтобы
может иметь все показания в той же картине.

Первый пример — асинхронный двигатель настольного шлифовального станка с номинальной мощностью
230 В _AC, 50 Гц, 250 Вт.
В качестве последовательного резистора я использовал массив из семи мощных резисторов, установленных на
радиатор на 8,15 Ом — 150 Вт, который я обычно использую
в качестве фиктивной нагрузки для тестирования усилителей звука.
Как вы можете видеть на рисунке ниже, U ₁ = 239,5 В ,
U ₂ = 4,630 В и
У ₃ = 235,7 В 90 130 .

Настольный шлифовальный станок измеряется методом трех вольтметров.
Три мультиметра слева направо показывают U ₁ ,
U ₂ и U ₃ .
Резистор (вверху справа) имеет номинал 8,15 Ом — 150 Вт.
(нажмите, чтобы увеличить).

Подставив все эти значения в калькулятор, находим коэффициент мощности
cos(φ) = 0,82 , ток I = 0,57 А ,
полная мощность S = 134 ВА и активная мощность
P = 110 Вт .
Неудивительно, что этот двигатель использует менее половины своего номинального значения.
мощность, потому что простаивает и просто компенсирует собственные потери.
Энергопотребление будет увеличиваться при измельчении чего-либо.

Тот же настольный шлифовальный станок измеряется с помощью анализатора мощности переменного тока.
(нажмите, чтобы увеличить).

Для проверки этого три измерения вольтметра и расчет, тот же стенд
кофемолка снова измеряется с помощью анализатора мощности переменного тока: он показывает 109,8 Вт.
и 0,579 мА, что хорошо подтверждает наш результат (точность всех
приборов, используемых здесь, не лучше ±1%).

Второй пример — большой трансформатор для галогенной лампы, рассчитанный на
220 В _AC, 50-60 Гц, 400 ВА, без подключенной нагрузки
к его вторичной обмотке (трансформатор без нагрузки обычно достаточно индуктивный).
Здесь, поскольку трансформатор не имеет нагрузки и потребляет гораздо меньшую мощность,
последовательный резистор 165 Ом, 17 Вт.
Как вы можете видеть на картинке ниже, U ₁ = 239,7 В ,
U ₂ = 11,10 В и
U ₃ = 232,9 В .

Трансформатор (без нагрузки) измеряется тремя вольтметрами
метод.
Три мультиметра слева направо показывают U ₁ ,
U ₂ и U ₃ .
Резистор (вверху справа) рассчитан на 165 Ом – 17 Вт.
(нажмите, чтобы увеличить).

Подставив все эти значения в калькулятор, находим коэффициент мощности
cos(φ) = 0,60 , ток I = 67 мА ,
полная мощность S = 16 ВА и активная мощность
P = 9,4 Вт .

Тот же трансформатор (без нагрузки) при измерении мощности переменного тока
анализатор. (нажмите, чтобы увеличить).

Измерение активной мощности измерителем мощности переменного тока дает 90,46 Вт и
68,7 мА, что снова подтверждает наш расчет.

Если вам интересно, что находится в серой коробке, это просто сетевая розетка с двойным
полюсный переключатель и три перемычки.