Конденсаторы статические: Батареи статических конденсаторов (БСК)

Содержание

Батареи статических конденсаторов (БСК)

26 декабря

Внимание! Возможны действия мошеннического характера со стороны ООО «Правтрейд»

22 декабря

Коллектив компании «Матик‑электро» поздравляет с наступающими Новым годом и Рождеством! От всей души желаем вам процветания и новых успехов!

09 октября

Компания «Матик-электро» поставила на нефтеперерабатывающий завод ООО »ЛУКОЙЛ-Нижегороднефтеоргсинтез» автоматические установки компенсации реактивной мощности, оснащенные антирезонансными дросселями

Архив новостей

БСК 26 Мвар 110 кВ

БСК 104 Мвар 220 кВ

Главная/Компенсация реактивной мощности/Батареи статических конденсаторов (БСК)

Батареи статических конденсаторов (БСК) предназначены для повышения напряжения (на 3-4%) в сетях 6-220 кВ. Кроме этого БСК позволяют корректировать перетоки энергии и регулировать напряжение в энергосистеме за счет изменения реактивной мощности нагрузки.

БСК производятся на базе косинусных однофазных конденсаторов, путем их параллельно-последовательного соединения в звезду или треугольник в зависимости от режима работы нейтрали. Для ограничения тока при включении БСК оснащаются токоограничивающими реакторами (по одному на фазу). Защита БСК обеспечивается отключением головного выключателя. Сигнал на устройства РЗА для отключения головного выключателя в случае разбалланса поступает с трансформаторов тока ТФЗМ, которые подключаются в разрыв двух параллельных групп конденсаторов.

Другой метод защиты применяемый в БСК – с помощью трансформатора напряжения. Этот метод основан на том, что при выходе из строя оного из конденсаторов батареи, появляется напряжение на вторичной обмотке двух встречновключенных разрядных катушек. Такие катушки размещаются по две в каждой фазе.

Конструктивно БСК представляет собой группы силовых высоковольтных конденсаторов, собранные в стальных несущих блоках («кассетах»). «Кассеты» закрепляются на полимерных изоляторах. Защита от коррозии стальных несущих конструкций БСК обеспечивается их горячим цинкованием. БСК предназначенные для районов с повышенной сейсмоактивностью, изготавливаются с усиленной конструкцией. Повышение прочности несущей конструкции БСК достигается путем установки дополнительных опорных изоляторов диагонально для поглощения горизонтальных колебаний. Трансформаторы тока и токоограничивающие реакторы, как правило, размещаются на отдельных стойках.

Соединения элементов БСК выполняются гибкой медной шиной для предотвращения повреждения изоляторов при температурном сжатии/расширении или под воздействием электродинамических нагрузок. БСК изготавливаются для установки на улице или в быстровозводимом здании. БСК на напряжение 6-10 кВ могут размещаться в утепленном блок контейнере.

Общий вид БСК

1. Высоковольтный конденсатор	2. Опорный изолятор	3. Опорный изолятор
4. Медный проводник	5. Суппорт конденсаторов	6. Трансформатор тока
7. Реактор токоограничивающий	8. Железобетонные сваи

Батареи статических конденсаторов

№	Обозначение типономинала батареи	Напряжение номинальное, кВ	Напряжение максимально допустимое, кВ	Емкость номинальная, мкФ	Мощность номинальная, МВАр
1	БСК-6-2,7 УХЛ1	6	7,2	238,73	2,7
2	БСК-6-4 УХЛ1			353,68	4
3	БСК-6-5,4 УХЛ1			477,46	5,4
4	БСК-6-6 УХЛ1			530,52	6
5	БСК-6-6,7 УХЛ1			592,41	6,7
6	БСК-6-8 УХЛ1			707,36	8
7	БСК-6-9,4 УХЛ1			831,14	9,4
8	БСК-6-10 УХЛ1			884,19	10
9	БСК-6-12 УХЛ1			1061,03	12
10	БСК-6-13,5 УХЛ1			1193,66	13,5
11	БСК-10-2,5 УХЛ1	10	12	79,58	2,5
12	БСК-10-3,75 УХЛ1			119,37	3,75
13	БСК-10-5 УХЛ1			159,15	5
14	БСК-10-5,65 УХЛ1			179,85	5,65
15	БСК-10-7,5 УХЛ1			238,73	7,5
16	БСК-10-8,75 УХЛ1			278,52	8,75
17	БСК-10-10 УХЛ1			318,31	10
18	БСК-10-11,25 УХЛ1			358,10	11,3
19	БСК-10-12,5 УХЛ1			366,06	11,5
20	БСК-10-13,15 УХЛ1			418,58	13,2
21	БСК-10-15 УХЛ1	10	12	477,46	15
22	БСК-35-3,8 УХЛ1	35	40,5	9,87	3,8
23	БСК-35-5,1 УХЛ1			13,25	5,1
24	БСК-35-7,6 УХЛ1			19,75	7,6
25	БСК-35-10,2 УХЛ1			26,50	10,2
26	БСК-35-11,4 УХЛ1			29,62	11,4
27	БСК-35-15,2 УХЛ1			39,50	15,2
28	БСК-35-19 УХЛ1			49,37	19
29	БСК-110-12,5 УХЛ1	110	126	3,29	12,5
30	БСК-110-17 УХЛ1			4,47	17
31	БСК-110-25 УХЛ1			6,58	25
32	БСК-110-34 УХЛ1			8,94	34
33	БСК-110-37,5 УХЛ1			9,86	37,5
34	БСК-110-50 УХЛ1			13,15	50
35	БСК-110-63 УХЛ1			16,57	63
36	БСК-110-67 УХЛ1			17,63	67
37	БСК-110-75 УХЛ1			19,73	75
38	БСК-110-84 УХЛ1			22,10	84
39	БСК-110-91 УХЛ1			23,94	91
40	БСК-110-100 УХЛ1			26,31	100
41	БСК-110-113 УХЛ1			29,73	113
42	БСК-110-125 УХЛ1			32,88	125
43	БСК-110-134 УХЛ1			35,25	134
44	БСК-110-143 УХЛ1			37,62	143
45	БСК-110-156 УХЛ1			41,04	156
46	БСК-220-25 УХЛ1	220	252	1,64	25
47	БСК-220-33,5 УХЛ1			2,20	33,5
48	БСК-220-50 УХЛ1			3,29	50
49	БСК-220-67 УХЛ1			4,41	67
50	БСК-220-75 УХЛ1			4,93	75
51	БСК-220-100 УХЛ1			6,58	100
52	БСК-220-125 УХЛ1			8,22	125
53	БСК-220-134 УХЛ1			8,81	134
54	БСК-220-150 УХЛ1			9,86	150

3 различных способа повышения коэффициента мощности

Х. только что закончила школу в Дубае. Прочитайте ее обзор о том, как улучшить Power Factor. Она дает вам 3 способа сделать это, и это хорошая статья, возвращающая к основам. Наслаждаться!

Коэффициент мощности — очень распространенный термин в электротехнике, поскольку он определяет эффективность электрической системы. Это слово вы услышите только при работе с цепями переменного тока, как показывает его простая формула:

Очень важно, чтобы коэффициент мощности оставался близким к единице, так как это указывает на более высокий КПД системы. Итак, сегодня мы обсудим 3 различных способа улучшения коэффициента мощности, которые широко используются в промышленных системах:

Статические конденсаторы

Одним из известных факторов, уменьшающих коэффициент мощности, является отстающий ток, возникающий из-за индуктивных нагрузок. Для улучшения коэффициента мощности статические конденсаторы устанавливаются параллельно оборудованию, работающему на низком коэффициенте мощности. Опережающий ток, потребляемый такими конденсаторами, нейтрализует или корректирует отстающую реактивную составляющую тока нагрузки.

Статические конденсаторы имеют много преимуществ, поскольку они легкие, простые в установке, имеют низкие потери и требуют меньше обслуживания. Однако недостатки весьма заметны: при превышении напряжения конденсаторы будут быстро повреждены, а их ремонт будет дорогостоящим. Также они имеют меньший срок службы (8-10 лет).

Синхронный конденсатор

Еще один способ улучшить коэффициент мощности — использовать трехфазный синхронный двигатель, работающий без нагрузки при перенапряжении. Эта установка известна как синхронный конденсатор. Интересно то, что синхронный двигатель может работать с опережающим, отстающим или единичным коэффициентом мощности. Если присутствует индуктивная нагрузка, то конденсатор будет подключен к стороне нагрузки и будет действовать как конденсатор для коррекции коэффициента мощности.

изображение: gegridsolutions. com (нажмите, чтобы увеличить)

Синхронный конденсатор имеет много преимуществ, поскольку он требует минимального обслуживания, может работать до 25 лет и не подвержен влиянию гармоник. Однако к его недостаткам можно отнести высокие эксплуатационные расходы, стоимость и шумность. Также требуется дополнительное оборудование для пуска двигателя, так как он не имеет крутящего момента самозапуска.

Ускоритель фазы

Последний метод, помогающий улучшить коэффициент мощности, заключается в использовании возбудителя переменного тока, также известного как ускоритель фазы. Однако это можно использовать только для асинхронных двигателей, потому что обмотки статора двигателя потребляют ток, который отстает от 90° отстает от напряжения и приводит к низкому коэффициенту мощности. Единственным способом избавиться от этой проблемы было бы использование внешнего источника, обеспечивающего захватывающие ампер-витки.

image: sourcingelectricals.com

Ускоритель фазы помогает решить проблему, когда он подключен к цепи ротора двигателя. Возбуждающие ампер-витки, обеспечиваемые опережителем, находятся на частоте скольжения. Опережающий коэффициент мощности также может быть получен за счет большего количества ампер-витков.

Основным преимуществом использования фазовращателя является снижение реактивной мощности, потребляемой двигателем. Его также можно использовать в местах, где синхронный конденсатор недопустим. Однако фазовращатель нельзя использовать для двигателей мощностью менее 200 л.с. что неэкономично.

Заключение

Это наиболее важные и полезные методы улучшения коэффициента мощности, но на рынке доступно множество других методов. Если у вас есть какой-либо другой метод, которым вы хотели бы поделиться, сообщите нам об этом в разделе комментариев!

Синхронный конденсатор с фазовым сдвигом коэффициента мощности

FacebookTwitterLinkedIn

2.6: Статические сети — Физика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 21512

Том Вайдеман
Калифорнийский университет в Дэвисе

Символические схемы

Мы обсуждали конденсаторы как теоретические конструкции, но на самом деле они являются обычными электрическими компонентами, используемыми во многих устройствах. Одним из типичных вариантов использования является источник «всплеска» электрической энергии, которая накапливается, когда источник напряжения заряжает ее на досуге, но затем высвобождается быстрее, чтобы выполнить какую-то работу, которую первоначальный источник напряжения не может выполнить так быстро. Мы увидим и другие варианты использования в следующей главе. Чтобы обсудить конденсаторы в этом практическом контексте, полезно ввести некоторые символические обозначения. Начнем с четырех символов:

эквипотенциал:

Сплошные непрерывные линии, соединяющие компоненты, представляют собой эквипотенциалы. Они могут состоять из отдельных линий или линий, ответвляющихся друг от друга. Хотя это обычно безвредно, думать об этих линиях как о проводящих проводах в физическом мире иногда может быть опасно, когда они встречаются впервые, поскольку мы будем использовать тот же набор символов позже, когда будем обсуждать электрический ток, где провода не являются проводниками. эквипотенциалы. Кроме того, проблемы легче решать, если помнить, что все, что соединено прямыми линиями, имеет одинаковый потенциал, а не просто канал потока заряда.

переключатель:

Этот компонент позволяет говорить о процессах, связанных с подключением и отключением других компонентов. Когда переключатель замкнут, он просто становится эквипотенциальным.

конденсатор:

Символ выглядит как вид сбоку конденсатора с плоскими пластинами, но он может представлять любую геометрию конденсатора, с диэлектриком внутри или без него. Обратите внимание, что соединение «пластины» прямой линией предполагает, что они имеют одинаковый потенциал (и так оно и есть), но поскольку между двумя пластинами есть зазор, они, конечно, не имеют одного и того же потенциала. Это первый из многих компонентов, с которыми мы столкнемся, которые обычно связаны с разностью потенциалов от одной стороны к другой.

батарея:

До сих пор мы говорили о том, чтобы «удерживать конденсатор при постоянной разности потенциалов», в то время как мы делаем такие вещи, как раздвигаем пластины или вставляем диэлектрик.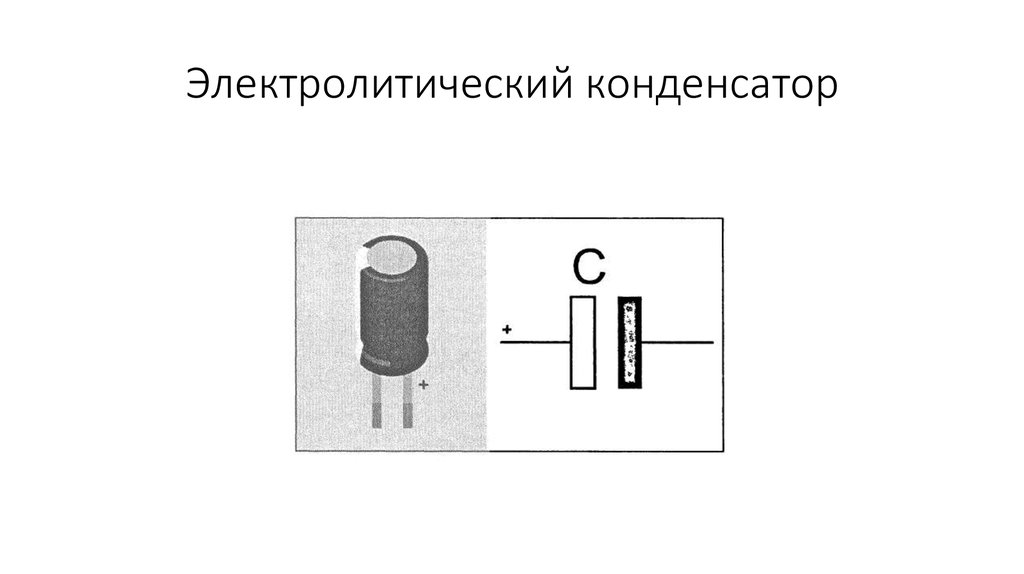 Нам больше не потребуется этот громоздкий язык, так как именно в этом заключается функция батарейки. Когда заряды входят в конденсатор или выходят из него, разность потенциалов (или напряжение 90 099 ) на пластинах изменяется, но две «пластины» батареи, показанные на символе, всегда остаются с одной и той же разностью потенциалов. Если одна сторона батареи соединена эквипотенциалом с одной стороной компонента, то эта сторона компонента остается под потенциалом, обеспечиваемым батареей. Если для поддержания этого потенциала требуется движение заряда, батарея подает или принимает заряд по мере необходимости. [ Следует отметить, что существует несколько символов, которые могут встречаться для обозначения батарей. «–» и «+» в показанном символе на самом деле лишние и не всегда появляются — большая «пластина» всегда имеет более высокий потенциал. Кроме того, символ с более чем двумя «пластинками» (чередующимися в размер) часто используется для обозначения батареи. ]

Эквивалентная емкость

Далее мы объединим несколько компонентов вместе, соединенных эквипотенциалами. Цепь представляет собой замкнутый контур компонентов и эквипотенциалов. Часто эти системы компонентов включают разветвления эквипотенциалы, что приводит к множеству замкнутых контуров.Такая система представляет собой комбинацию многих контуров, и часто вся система также называется цепью, но более точным термином для такой системы является сеть . Читатель, вероятно, встретится с обоими терминами для описания таких систем в этой работе.

Для анализа этих систем полезно разработать некоторые инструменты для исследования фрагментов цепи из нескольких конденсаторов (каждый из которых может иметь разную емкость). Самый простой такой фрагмент — тот, в котором они соединены «последовательно», как показано на рисунке ниже.

Рисунок 2.6.1 – Конденсаторы серии

На диаграмме с цветовой кодировкой слева выделены эквипотенциалы и пластины с одинаковым потенциалом – левая пластина конденсатора №1 находится под потенциалом \(V_A\), правая пластина конденсатора №1 и левая пластина конденсатора №2 находится под потенциалом \(V_B\), а правая пластина конденсатора №2 – под потенциалом \(V_C\). Таким образом, напряжение на конденсаторах:

\[V_1 = V_A-V_B\;,\;\;\;\;\;V_2=V_B-V_C \]

Это означает, что разность потенциалов между эквипотенциалами на два конца комбинации конденсаторов — это просто сумма напряжений на конденсаторах:

\[V_{tot} = V_A-V_C = \left(V_A-V_B\right) + \left(V_B-V_C\right) = V_1+V_2\]

Как насчет заряда каждого конденсатора? Итак, мы знаем, что пластины одного конденсатора имеют одинаковый заряд с разными знаками. Синий сегмент изолирован, поэтому не может получать никакого внешнего заряда, а это означает, что какой бы заряд ни находился на правой обкладке конденсатора № 1, такое же количество заряда с противоположным знаком находится на левой обкладке конденсатора № 2. Следовательно, заряд каждого конденсатора в этой конфигурации одинаков.

Всякий раз, когда два или более конденсатора расположены таким образом, что они удовлетворяют вышеуказанным свойствам (напряжение на комбинации равно сумме напряжений каждого из них, а заряды одинаковы на всех из них), мы говорим что эти конденсаторы в s eries . У нас есть общая разность напряжений для комбинации и единичное количество заряда на пластине, поэтому мы можем определить эквивалентную емкость для схемы. А именно:

\[\слева. \begin{array}{l} Q=C_{eq}V_{tot} \\ Q=C_1V_1 \\ Q=C_2V_2 \\ V_{tot}=V_1+V_2 \end{массив} \right\}\;\ ;\; \dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} \;\;\;\text{(series)}\]

Обратите внимание, что если есть более двух конденсаторов последовательно, нам нужно только добавить дополнительные обратные условия.

Предупреждение

Нередко ошибочно объявляют, что конденсаторы соединены последовательно, просто потому, что они «выглядят последовательными», хотя на самом деле они не соединены последовательно. Важно убедиться, что критерии, включающие напряжение и заряд, действуют, прежде чем вычислять эквивалентную последовательную емкость.

Другое базовое расположение конденсаторов меняет местами заряд и напряжение, как показано на рисунке ниже.

Рисунок 2. 6.1-конденсаторы в параллельном

снова правый диаг. Цветовые коды у эквинологии, и в этот время мы видим, что у двух капусов есть правые диаграммы. разность потенциалов на них:

\[V_1 = V_A-V_B = V_2\]

Что касается заряда, то каждая пластина должна получить заряд извне (через эквипотенциалы), и на конденсаторы пойдет разное количество заряда, и общий заряд, подведенный к этой системе, будет равен сумме зарядов, подведенных к каждому отдельному конденсатору. Когда эти два критерия выполняются, мы говорим, что конденсаторы равны параллельно .

Alert

Это еще одно предупреждение о том, что два конденсатора должны быть включены параллельно просто потому, что они так выглядят. Самый простой тест для параллельных конденсаторов — проверить, соединяет ли эквипотенциал напрямую обе пластины одного конденсатора с соответствующими пластинами другого конденсатора.

Для эквивалентной емкости складываем два новых критерия и получаем новое соотношение:

\[\left. \begin{array}{l} Q_{tot}=C_{eq}V \\ Q_1=C_1V \\ Q_2=C_2V \\ Q_{tot}=Q_1+Q_2 \end{массив} \right\}\;\ ;\; C_{eq} = C_1 + C_2\;\;\;\text{(параллельно)}\]

Если параллельно подключено более двух конденсаторов, то, конечно, эквивалентная емкость представляет собой сумму всех отдельных емкостей.

Пример \(\PageIndex{1}\)

Покажите, что как в последовательном, так и в параллельном случае энергия, запасенная в эквивалентном конденсаторе, равна сумме энергий в отдельных конденсаторах.

Раствор: В последовательном случае заряд обоих конденсаторов одинаков, поэтому общая накопленная энергия составляет: 92 \номер\]

Сети конденсаторов

То, что у нас есть уравнение только для пары конденсаторов, не означает, что мы можем решать задачи только с двумя конденсаторами. Мы можем решать гораздо большие сети в режиме начальной загрузки, комбинируя пары конденсаторов для формирования эквивалентных конденсаторов, затем рассматривая эквивалентные конденсаторы, как если бы они были «настоящими» конденсаторами, и комбинируя из них в новые эквивалентные конденсаторы. После того, как произошло достаточное сокращение, можно сделать вывод о том, сколько заряда уходит от батареи, а затем «действовать в обратном направлении», имея в виду, что количество заряда на эквивалентном конденсаторе такое же, как заряд на составляющих его конденсаторах, если они находятся в разомкнутом состоянии. последовательно, а разность напряжений на эквивалентном конденсаторе такая же, как и на составляющих его конденсаторах, если они подключены параллельно. Как только все эквивалентные конденсаторы размотаны, заряды и напряжения (и, следовательно, также энергии) известны для каждого конденсатора в сети. Овладение этим процессом — вопрос практики, поэтому вот пример…

Пример \(\PageIndex{2}\)

Для сети на рисунке вычислите долю общей энергии, поставляемой батареей, которая идет на каждый из отдельных конденсаторов.

Раствор

Мы начнем с обозначения напряжения на аккумуляторе ‘\(V\)’. Он выпадет из окончательного ответа, но нам нужно кое-что добавить в алгебру. Теперь начинаем процесс объединения конденсаторов для создания единой эквивалентной емкости для сети.

Может показаться, что \(1C\) и \(3C\) соединены последовательно, но это не так! Эквипотенциал, который соединяется с левой пластиной \(3C\), разделяется и соединяется с правыми пластинами двух конденсаторов. Это означает, что сумма зарядов на правых пластинах \(1C\) и \(2C\) равна отрицательному заряду левой пластины \(3C\). Поскольку заряды для \(1C\) и \(3C\) не равны, они не могут быть соединены последовательно. С другой стороны, отслеживание эквипотенциала, присоединенного к левой пластине \(1C\), идет к левой пластине \(2C\), а отслеживание эквипотенциала, прикрепленного к правой пластине \(1C\), идет к правой пластине \(2C\), поэтому они имеют одинаковые падения напряжения и находятся параллельно. Заменяем их эквивалентной емкостью (которая представляет собой просто сумму их емкостей) и перерисовываем диаграмму:

Очевидно, что эти конденсаторы теперь включены последовательно, поэтому мы объединим их, чтобы получить один эквивалентный конденсатор:

\[\dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} = \dfrac{2}{3C}\;\;\;\Rightarrow \;\;\; C_{eq} = \frac{3}{2}C\nonumber\]

С одним эквивалентным конденсатором, присоединенным к батарее, мы можем вычислить, сколько заряда покидает батарею, и количество энергии, поставляемой батареей: 92 \конец{массив} \номер\]

Теперь самое сложное – «раскрутка». Начнем с заряда, обеспечиваемого аккумулятором. Какой бы положительный заряд ни покидал аккумулятор, он собирается на правой пластине \(3C\) — больше никуда он не денется. Это сразу говорит нам о напряжении на \(3C\) и, следовательно, о накопленной на нем энергии.

\[\begin{array}{l} Q_3 = Q_{tot} = \frac{3}{2}CV && \Rightarrow && V_3 = \dfrac{Q_3}{3C} = \frac{1}{2 }V \\ U_3 = \frac{1}{2}\left(3C\right)V_3^2 && \Rightarrow && U_3 = \frac{3}{8}CV^2 \end{array} \nonumber\]

Эквивалентный конденсатор для \(1C\) и \(2C\) включен последовательно с \(3C\), поэтому сумма их напряжений должна равняться общему напряжению на комбинации, которое равно напряжению батареи . Поэтому неудивительно, что напряжение на эквивалентном конденсаторе для \(1C\) и \(2C\) также равно \(\frac{1}{2}V\). Два отдельных конденсатора в этой параллельной комбинации имеют ту же разность напряжений, что и разность напряжений их комбинации, поэтому мы можем вычислить энергию, хранящуюся в каждом из них (нам не нужно вычислять заряд каждого конденсатора, но мы могли бы легко делаем так, если хотим) 92} = \dfrac{1}{2}\end{массив}\номер\]

Обратите внимание, что сумма этих дробей равна 1, что подтверждает, что общая энергия, покидающая батарею, равна сумме энергий трех конденсаторов.

Существуют и другие приложения этих инструментов, которые не попадают в этот шаблон. Такого рода примеры требуют некоторого размышления о том, применимы ли они последовательно или параллельно. Вот пара немного более необычных примеров…

Пример \(\PageIndex{3}\)

Плоский конденсатор с вакуумом между пластинами заряжается путем подключения его к батарее 12 В, а после полной зарядки батарея отключается. Затем изолятор толщиной, равной половине ширины зазора в исходном конденсаторе, зажат между двумя тонкими проводящими пластинами и вставлен между пластинами исходного конденсатора. После того, как это сделано, измеряется напряжение во всей системе, равное 8,4 В. Найдите диэлектрическую проницаемость изолятора.

Раствор

Размещение диэлектрика между пластинами создает три отдельные области внутри конденсатора. Благодаря тому, что электрическое поле перпендикулярно пластинам, каждый конец диэлектрика является эквипотенциальным, а это означает, что мы можем рассматривать три области, как если бы они были отдельными конденсаторами с параллельными пластинами, соединенными последовательно. Центральный конденсатор имеет диэлектрик, а внешние конденсаторы имеют вакуумные промежутки. Ради математических расчетов мы назовем размер зазора исходного конденсатора \(2d\) (составляя толщину диэлектрика \(d\) и толщину двух внешних конденсаторов \(\frac{1 {2}d\). Мы назовем площадь пластин \(A\), а диэлектрическую проницаемость (которую мы ищем) \(\каппа\).

а. Емкость оригинального конденсатора:

\[C_{до} = \dfrac{\epsilon_oA}{2d}\не число\]

Рассматривая новую конфигурацию как три последовательных конденсатора и вычисляя эквивалентную емкость, получаем:

\[\dfrac{1}{C_{после}} = \dfrac{1}{C_1}+\dfrac{1}{C_2}+\dfrac{1}{C_3} = \dfrac{\frac{1} {2}d}{\epsilon_oA}+\dfrac{d}{\kappa\epsilon_oA} + \dfrac{\frac{1}{2}d}{\epsilon_oA} \;\;\;\Rightarrow\; \;\; C_{после} = \dfrac{\epsilon_oA}{d}\left[\dfrac{\kappa}{\kappa + 1}\right]\nonumber\]

Когда пластины отсоединены от батареи, заряд на пластинах конденсатора в этом процессе остается постоянным (ему деваться некуда!). Уравнивание зарядов дает нам соотношение емкостей до и после относительно заданных напряжений:

\[Q=C_{до}V_{до}=C_{до}V_{до}\;\;\;\Стрелка вправо\;\;\; \dfrac{C_1}{C_2} = \dfrac{V_2}{V_1} \;\;\;\Rightarrow\;\;\; \dfrac{\dfrac{\epsilon_oA}{2d}}{\dfrac{\epsilon_oA}{d}\left[\dfrac{\kappa}{\kappa + 1}\right]} = \dfrac{\kappa+1 }{2\каппа} = \dfrac{8. 4V}{12V} \;\;\;\Rightarrow\;\;\; \каппа = 2,5\нечисло\]

Пример \(\PageIndex{4}\)

Два конденсатора отдельно подключаются к батареям до полной зарядки, а затем отключаются. В этот момент конденсаторы имеют одинаковый заряд, но конденсатор №1 хранит в три раза больше энергии, чем конденсатор №2. Затем два конденсатора соединяются друг с другом таким образом, что положительный вывод одного конденсатора соединяется с положительным выводом другого, а также с отрицательными выводами.

В каком направлении течет заряд при таком соединении и какая часть заряда вытекает из разряжающегося конденсатора?
Если разность напряжений между положительными и отрицательными пластинами после подключения конденсаторов равна \(В\), найдите напряжение на каждом конденсаторе до их подключения через \(В\).
Найдите долю изменения энергии в системе, когда заряды перестраиваются после соединения конденсаторов. Это прибыль или потеря? 92}{2C_2}\;\;\;\Стрелка вправо\;\;\;C_2 = 3C_1\номер\]

Когда они соединены вместе, это происходит параллельно, потому что пластины одного конденсатора соединены с их аналогами на другом конденсаторе с эквипотенциалом. Это означает, что их пластины теперь вынуждены иметь одинаковую разность потенциалов. Два конденсатора с одинаковой разностью напряжений будут удерживать заряды, пропорциональные их емкостям:

\[\left.\begin{array}{l} Q_1=C_1V \\ Q_2=C_2V \end{array} \right\}\;\;\; \dfrac{Q_1}{Q_2} = \dfrac{C_1}{C_2} \номер\]

Итак, конденсатор № 2 будет иметь в 3 раза больше заряда на своих пластинах, чем конденсатор № 1, когда заряд перестанет перестраиваться. Они начали с одинакового заряда, поэтому, чтобы конденсатор № 2 имел в 3 раза больше заряда, чем № 1, № 1 должен был потерять половину своего начального заряда. С точки зрения нашего определенного значения \(Q\), конденсатор №1 заканчивается \(\frac{1}{2}Q\), а конденсатор №2 заканчивается \(\frac{3}{2}Q \).

б. У нас есть условия до и после, и их сравнение дает наши ответы:

\[\left.\begin{array}{l} до: && Q=C_1V_1 \\ после: && \frac{1}{2}Q = C_1V \end{array} \right\}\;\; V_1 = 2V\номер\]

\[\left.\begin{array}{l} до: && Q=C_2V_2 \\ после: && \frac{3}{2}Q = C_2V \end{array} \right\}\;\; V_2 = \frac{2}{3}V\номер\]

г. Запись полных энергий до и после через \(Q\) и \(V\) дает:

\[\begin{array}{l} перед: && U=\frac{1}{2}QV_1 + \frac{1}{2}QV_2 = \frac{1}{2}Q\left(2V \right) + \frac{1}{2}Q\left(\frac{2}{3}V\right) = \frac{4}{3}QV \\ после: && U=\frac{1} {2}Q_1V + \frac{1}{2}Q_2V = \frac{1}{2}\left(\frac{1}{2}Q\right)V + \frac{1}{2}\left (\frac{3}{2}Q\right)V = QV \end{массив}\nonumber\]

Система падает до трех четвертей своей первоначальной энергии, поэтому она теряет одну четверть того, с чего начала.

Куда уходит энергия? Просто ради аргумента предположим, что конденсаторы имеют вид пластин с параллельными пластинами, и что конденсатор № 2 имеет в три раза большую емкость, чем конденсатор № 1, потому что его пластины имеют в три раза большую площадь. При одинаковых зарядах на каждом конденсаторе это означает, что плотность заряда на конденсаторе №1 в три раза больше, чем на конденсаторе №2. Тот факт, что на конденсаторе №1 заряды сжаты плотнее, является причиной того, что там запасается больше потенциальной энергии. Если позволить зарядам равномерно перераспределиться за счет подключения конденсаторов, система перейдет в состояние с более низкой потенциальной энергией. С точки зрения сил, отталкивание зарядов от конденсатора № 1 превышает отталкивание этих зарядов от конденсатора № 2, поэтому чистая работа выполняется электрической силой при достижении нового состояния (уменьшение потенциальной энергии), и поскольку мы предполагаем, что кинетическая энергия, переданная зарядам, в конечном итоге рассеивается, энергия в системе в конце меньше, чем в начале.

Эта страница под названием 2.6: Статические сети распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Томом Вайдеманом непосредственно на платформе LibreTexts.