Содержание
Конденсатор
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
Конденсатор — это устройство для накопления электрического заряда; он состоит из двух проводников (обкладок), расположенных близко друг к другу, но не соприкасающихся. Типичный плоский конденсатор представляет собой пару параллельных пластин площадью А, разделенных небольшим промежутком d (рис. 25.1, а). Часто пластины, разделяют прокладкой из бумаги или другого диэлектрика (изолятора) и сворачивают в рулон (рис. 25.1,6).
Предположим, что конденсатор подключен к источнику напряжения, например к батарее. (Батарея — это устройство, на клеммах которого поддерживается относительно постоянная разность потенциалов). Подсоединенный к батарее конденсатор быстро заряжается: одна его обкладка приобретает положительный заряд, другая-равный по величине отрицательный (рис. 25.2).
Заряд, приобретаемый каждой из обкладок конденсатора, пропорционален разности потенциалов Vba:
Q = CVba (25. 1)
Коэффициент пропорциональности С называется емкостью конденсатора. Единица емкости, кулон на вольт, называется фарад (Ф). На практике чаще всего
применяются конденсаторы емкостью от 1 пФ (пикофарад, 10-12Ф) до 1 мкФ (микрофарад, 10-6 Ф). Формулу (25.1) впервые вывел Вольт в конце XVIII в.
Емкость С служит характеристикой данного конденсатора. Величина емкости С зависит от размеров, формы и взаимного расположения обкладок, а также от вещества, заполняющего промежуток между обкладками. В этом разделе мы будем считать, что между обкладками находится вакуум или воздух.
Емкость конденсатора, согласно (25.1), можно определить экспериментально, непосредственно измерив заряд Q пластины при известной разности потенциалов Vba.
Если геометрическая конфигурация конденсаторов достаточно проста, то можно определить емкость С аналитически.
Поскольку плотность заряда равна σ = Q/A, то
Напряженность электрического поля связана с разностью потенциалов соотношением
Мы можем взять интеграл от одной пластины до другой вдоль траектории, направленной навстречу силовым линиям:
Установив связь между Q и Vba, выразим теперь емкость С через геометрические параметры:
Справедливость полученного вывода очевидна: чем больше площадь А, тем «свободнее» разместятся на ней заряды, отталкивание между ними будет меньше и каждая пластина сможет удерживать больший заряд.
одной пластине будут притягивать заряды на другой: на пластины от батареи поступает меньше заряда и емкость оказывается меньше.
Обратим также внимание, что формула справедлива при использовании в качестве диэлектрика — вакуума. Для других изоляторов используется коэффициент диэлектрической проницаемости К.
Тогда, с учётом коэффициента, ёмкость конденсатора будет равна:
С = Кε0 A/d , либо С = εA/d
Например, для некоторых диэлектриков коэффициент К будет равен:
Вакуум: К = 1.0000
Воздух (1 атм): К = 1.0006
Парафин: К = 2.2
Эбонит: К = 2.8
Пластик (поливинильный): К = 2.8-4.5
Бумага: К = 3-7
Кварц: К = 4.3
Стекло: К = 4-7
Фарфор: К = 6-8
Слюда: К = 7
Более подробно это будет рассмотрено далее в публикации — «Диэлектрики».
Продолжение следует. Коротко о следующей публикации:
Последовательное и параллельное соединения конденсаторов.
Конденсаторы можно соединять различными способами. На практике это используют очень часто, и емкость комбинации конденсаторов зависит от того, как они соединены. Два основных способа соединения — параллельное и последовательное.
Альтернативные статьи:
Дизель-генератор,
Асинхронный генератор.
Замечания и предложения принимаются и приветствуются!
Глава 20. Конденсаторы
Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.
Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):
|
(20.1) |
Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.
Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см.
|
(20.2) |
Разность потенциалов между пластинами равна
|
(20.3) |
где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора
|
(20.4) |
Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает
|
(20.5) |
Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов.
Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов
|
(20.6) |
Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .
Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов
|
(20.7) |
Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна
|
(20.8) |
С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:
|
(20.9) |
Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.
Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).
Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).
Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в задаче 20.1.4
(ответ 4).
Согласно определению электрической емкости имеем в задаче 20.1.5
(ответ 2).
Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20.1.6) его емкость увеличивается в 3 раза (ответ 1).
При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул
где и — новый заряд конденсатора (ответ 3).
Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).
В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.2)
то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что
произведение от расстояния между пластинами не зависит (см. формулу (20.4)).
Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.
При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20.2.2) одинаковыми будут напряжения на каждом из них (ответ 3).
Поскольку конденсатор в задаче 20.
|
(1) |
Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ 1).
В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)
Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)
В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора.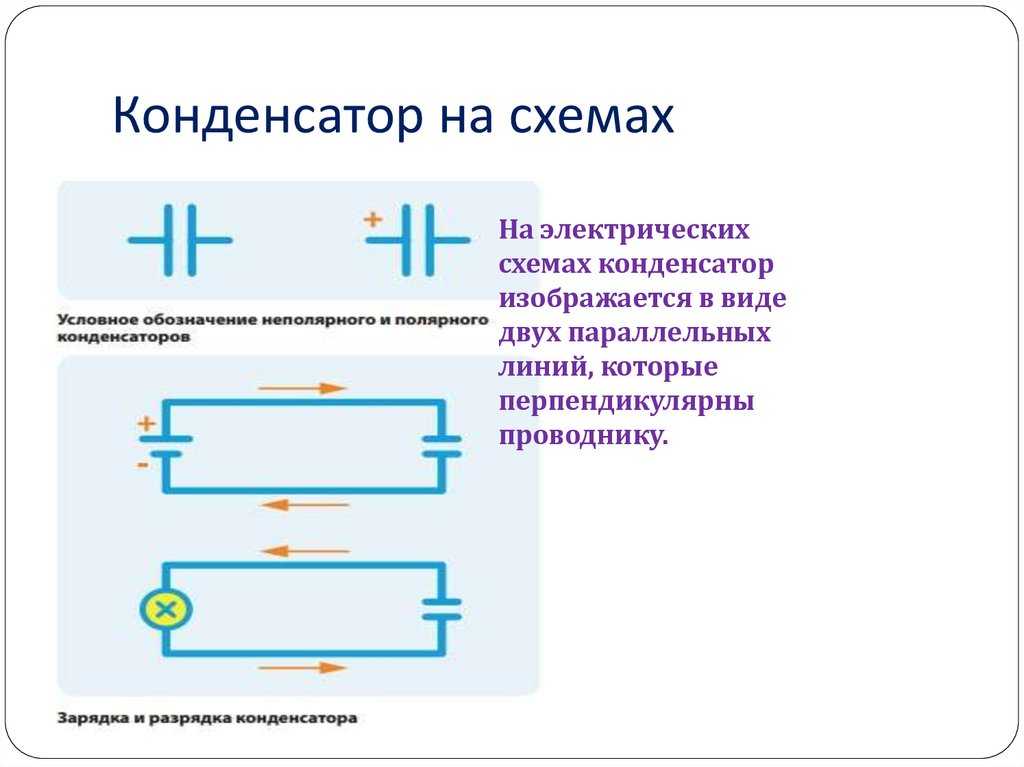
Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).
Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).
В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).
Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно.
Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:
где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора
(ответ 4).
Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.
Конденсатор Определение и значение | Dictionary.com.
[ kuh-pas-i-ter ]
/ kəˈpæs ɪ tər /
Сохранить это слово!
Показывает уровень оценки в зависимости от сложности слова.
сущ. Электричество.
устройство для накопления и удержания заряда электричества, состоящее из двух одинаково заряженных проводящих поверхностей, имеющих противоположные знаки и разделенных диэлектриком.
ВИКТОРИНА
ВЫ ПРОЙДЕТЕ ЭТИ ВОПРОСЫ ПО ГРАММАТИКЕ ИЛИ НАТЯНУТСЯ?
Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!
Вопрос 1 из 7
Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.
Также называется конденсатором.
Происхождение конденсатора
Впервые зафиксировано в 1925–1930 гг.
Слова рядом с конденсатором
емкость, емкость, емкость, емкостная связь, емкостное реактивное сопротивление, конденсатор, емкость, крышка и колокольчики, крышка и платье, крышка и торговля, Капаней
Dictionary.com Полный текст
Основано на словаре Random House Unabridged Dictionary, © Random House, Inc. 2022
Как использовать конденсатор в предложении
-
Его объяснения всегда верны, даже когда речь идет о «потоковом конденсаторе» и прочей чепухе с путешествиями во времени.
Кристофер Ллойд по-прежнему играет персонажей, которые расстроены — и больше, чем жизнь|Карен Хеллер|26 августа 2021 г.|Washington Post
-
Сообщение «Подготовьтесь к путешествию во времени с этим конденсатором потока» впервые появилось в Popular Science.
Подготовьтесь к путешествию во времени с этим потоковым конденсатором|Куинн Гавронски|13 июля 2021 г.|Popular-Science
-
Хотя возможности потокового конденсатора полностью вымышлены и представляют собой исключительно забаву, нет ничего постыдного в том, чтобы заниматься научной фантастикой.
.
Подготовьтесь к путешествию во времени с этим конденсатором потока|Quinn Gawronski|13 июля 2021 г.|Popular-Science
-
Алюминиевые поверхности на стенах и потолке будут проводить электричество от конденсаторов, когда оно возвращается к медному столбу в центре комната.
Беспроводное зарядное устройство Xiaomi дальнего радиуса действия показывает проблеск беспроводного будущего|Стэн Хорачек|1 февраля 2021 г.|Popular-Science
-
Конденсатор также питал датчик, который измерял соленость пота этого человека.
Работая в поте лица, однажды можно включить устройство|Кэролин Уилке|29 июня 2020|Новости науки для студентов
-
Чтобы вернуться в настоящее, его конденсатор потока нуждался в провиденциальной молнии.
Хватит пытаться сбалансировать бюджеты!|Гарольд Эванс|28 июня 2010|DAILY BEAST
-
«Отличная работа у этих малышей», — прокомментировал Гейнс, проверяя цепи конденсаторов.
Небольшой мир M-75 | Ed M.
Clinton, Jr.
Британские определения словаря для конденсатора
Конденсатор
/ (Kəˈpæsɪtə) /
NOUN
ACCULERELER для устройства для ACCKELOL состоящий из двух проводящих поверхностей, разделенных диэлектриком. Бывшее название: конденсатор 9.0017
Английский словарь Коллинза — полное и полное цифровое издание 2012 г.
© William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins
Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения конденсатора
конденсатор
[ kə-păs′ĭtər ]
Устройство, состоящее из двух проводящих пластин
900 электрический изолятор (диэлектрик), предназначенный для удержания электрического заряда. Заряд накапливается, когда на пластины подается напряжение, создавая между ними электрическое поле. Ток может течь через конденсатор только при изменении напряжения на нем, а не когда оно постоянно. Конденсаторы используются в источниках питания, усилителях, процессорах сигналов, генераторах и логических элементах.
Научный словарь American Heritage®
Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Культурные определения конденсатора
конденсатор
[ (kuh-pas-i-tuhr) ]
Устройство, используемое в электрических цепях. Конденсатор накапливает электрический заряд в течение коротких промежутков времени, а затем возвращает его в цепь.
Новый словарь культурной грамотности, третье издание
Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Конденсатор и емкость. Определение, типы и применение
Конденсатор представляет собой электрический компонент, обладающий способностью накапливать энергию в виде электрических зарядов, создающих разность потенциалов, представляющую собой статическое напряжение, подобное небольшому перезаряжаемому аккумулятору.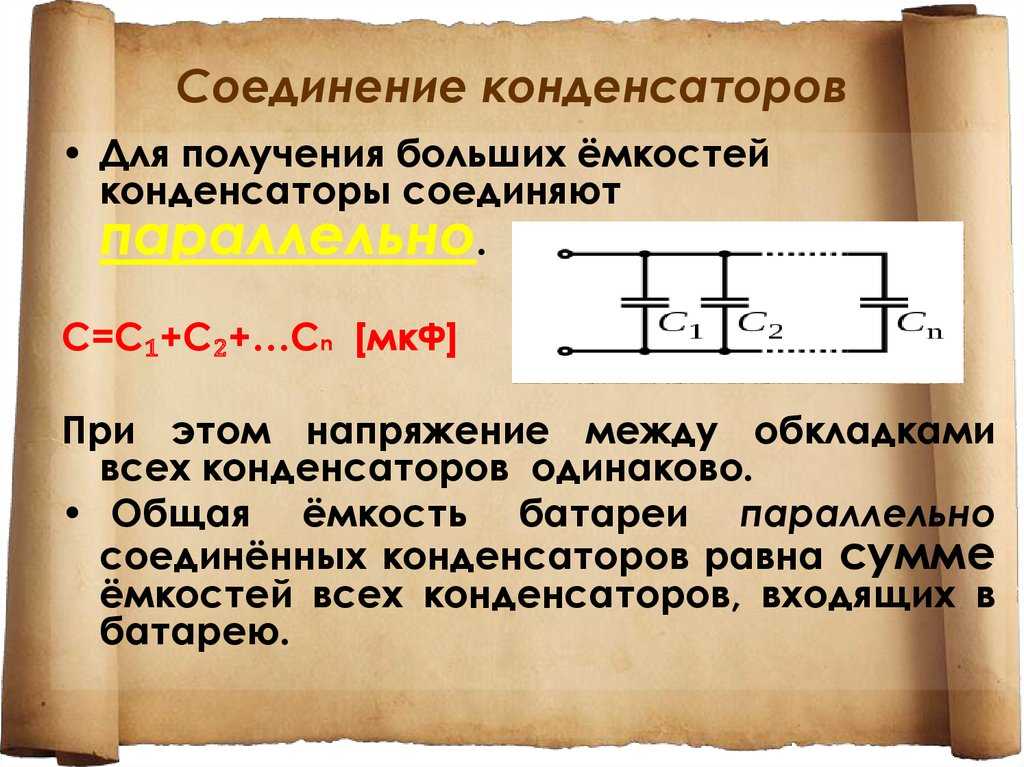
Самая простая конструкция конденсатора состоит из двух параллельных проводников (металлических пластин), разделенных диэлектрическим материалом. Когда к конденсатору подключается источник напряжения, пластина конденсатора заряжается. Металлическая пластина, прикрепленная к положительной клемме, будет заряжена положительно, а пластина, прикрепленная к отрицательной клемме, будет заряжена отрицательно.
(Изображение будет загружено в ближайшее время)
Обозначения конденсаторов
Типы конденсаторов
-
Пленочные конденсаторы: Пленочные конденсаторы — это конденсаторы, в которых в качестве диэлектрической среды используется пластиковая пленка. Они доступны практически любого номинала и напряжения до 1500 вольт. Они варьируются от 10% до 0,01% при любом допуске. Кроме того, пленочные конденсаторы бывают разных форм и стилей корпуса. Существует два типа пленочных конденсаторов: вывод радиального типа и вывод осевого типа.
-
Керамические конденсаторы. В керамических конденсаторах в качестве диэлектрического материала используется керамика. Он используется в высокочастотных цепях, таких как аудио в РЧ. В керамических конденсаторах можно получить как высокую, так и низкую емкость, изменяя толщину керамического диска.
-
Электролитические конденсаторы: Электролитические конденсаторы используют оксидный слой в качестве диэлектрического материала. Обладает широкой толерантностью. Существуют в основном два типа электролитических конденсаторов: танталовые и алюминиевые. Они доступны с рабочим напряжением примерно до 500 В, но максимальные значения емкости недоступны при высоком напряжении, а блоки с более высокой температурой доступны, но встречаются редко.
-
Переменный конденсатор: Переменные конденсаторы в основном используют воздух в качестве диэлектрической среды.
Переменный конденсатор — это конденсатор, емкость которого можно механически регулировать несколько раз. Например, эта форма конденсатора используется для установки резонансной частоты в LC-цепях, чтобы изменить радио для согласования импеданса в устройствах настройки антенны.
Определение емкости конденсатора
Накопление зарядов в проводниках вызывает разность потенциалов на конденсаторе. Количество накопленного заряда называется зарядоемкостью конденсатора. Эта емкость удержания заряда называется емкостью. Накопленный заряд в конденсаторе прямо пропорционален напряжению, развиваемому на конденсаторе:
Q ∝V
Q = C/V
C = Q/V
C – коэффициент пропорциональности, также называемый емкостью конденсатора. Единицей емкости является фарад (Ф) — 1 кулон на вольт.
(Изображение будет загружено в ближайшее время)
Значение емкости зависит от физических характеристик, площади пластин конденсатора «A», расстояния между пластинами «d» и диэлектрической проницаемости диэлектрической среды «ε».
\[C = \varepsilon \times \frac{A}{d}\] 92}{2}\]
Конденсатор в серии
Суммарная емкость конденсаторов, соединенных последовательно C1, C2, C3,.. :
\[\frac{1}{C_{Total}}\] = \[\frac{1}{C_{1}}\] + \[\frac{1}{C_{2}}\] + \[\frac{1}{C_{3}}\] + …
(Изображение будет загружено в ближайшее время)
Конденсатор, включенный параллельно
Суммарная емкость конденсаторов, соединенных параллельно C1, C2, C3,.. :
(Изображение будет загружено в ближайшее время)
CTotal = C1+C2+ C3+…
Факторы, влияющие на емкость
-
Площадь поверхности: Площадь поверхности двух пластин влияет на значение емкости. Чем выше значение площади поверхности, тем выше емкость.
-
Расстояние: Расстояние между пластинами влияет на значение емкости.
Чем меньше значение расстояния, тем выше емкость.
-
Диэлектрическая среда: тип материала, разделяющего две пластины, называемые «диэлектриком». Чем выше диэлектрическая проницаемость диэлектрика, тем выше значение емкости.
Применение конденсатора
Конденсаторы применяются как в электротехнике, так и в электронике. Они используются для нескольких вещей, таких как фильтры, системы накопления энергии, пускатели двигателей, устройства обработки сигналов и т. д.
-
Конденсаторы используются для хранения энергии, которую устройство может использовать для временных отключений электроэнергии, когда им требуется дополнительная мощность. .
-
Конденсаторы используются для блокировки постоянного тока после полной зарядки и позволяют переменному току проходить через цепь цепи.
-
Конденсаторы используются в качестве датчиков для нескольких вещей, таких как измерение влажности, уровня топлива, механического напряжения и т. д.
-
Конденсаторы можно использовать в цепи, зависящей от времени. Это может быть подключено к любой светодиодной или акустической системе, и вполне вероятно, что любой мигающий свет / регулярный звуковой сигнал использует времязадающий конденсатор.
Интересные факты
-
Конденсаторы с высокой емкостью изготовлены из материала с высокой диэлектрической проницаемостью.
-
Конденсатор может принимать и временно накапливать энергию из цепи. Затем конденсатор вернет энергию в цепь позже.
Как подготовиться к экзаменам по этой теме?
Подготовка к экзамену не обходится без Vedantu.
 .
.  Clinton, Jr.
Clinton, Jr. 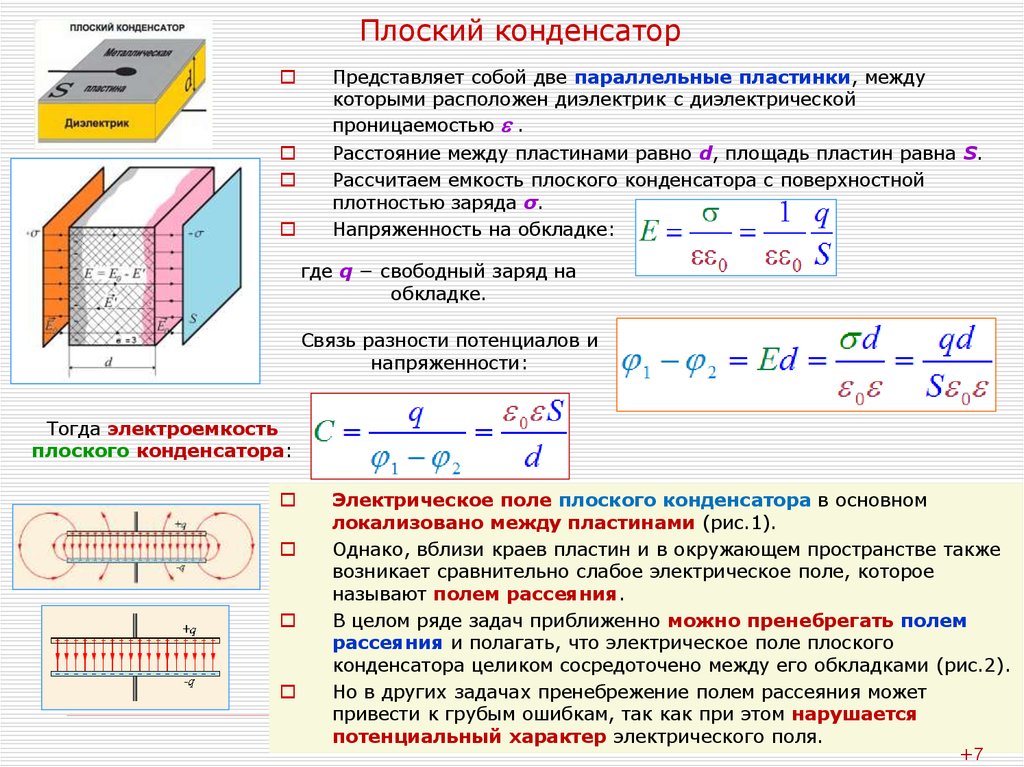
 Переменный конденсатор — это конденсатор, емкость которого можно механически регулировать несколько раз. Например, эта форма конденсатора используется для установки резонансной частоты в LC-цепях, чтобы изменить радио для согласования импеданса в устройствах настройки антенны.
Переменный конденсатор — это конденсатор, емкость которого можно механически регулировать несколько раз. Например, эта форма конденсатора используется для установки резонансной частоты в LC-цепях, чтобы изменить радио для согласования импеданса в устройствах настройки антенны.  Чем меньше значение расстояния, тем выше емкость.
Чем меньше значение расстояния, тем выше емкость. 

Добавить комментарий