Электрический конденсатор. Виды конденсаторов. Конденсатор переменного токаСопротивление конденсатораГоспода, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета. Сразу оговорюсь про одну важную вещь. Вообще говоря, реальный конденсатор обладает помимо емкостного сопротивления еще резистивным и индуктивным. На практике все это надо обязательно учитывать, потому что возможны ситуации (обычно связанные с ростом частоты сигнала), когда конденсатор перестает быть конденсатором и превращается… в некое подобие катушки индуктивности Давайте представим, что у нас есть конденсатор, который включен в цепь с переменным током. В цепи больше нет никаких компонентов, только один конденсатор и все (рисунок 1).
Рисунок 1 – Конденсатор в цепи переменного тока К его обкладкам приложено некоторое переменное напряжение U(t), и через него течет некоторый ток I(t). Зная одно, можно без проблем найти другое. Для этого надо всего лишь вспомнить прошлую статью про конденсатор в цепи переменного тока, там мы про все это довольно подробно говорили. Будем полагать, что ток через конденсатор изменяется по синусоидальному закону вот так
В прошлой статье мы пришли к выводу, что если ток изменятся вот по такому закону, то напряжение на конденсаторе должно меняться следующим образом
Пока что ничего нового мы не записали, это все дословное повторение выкладок из предыдущей статьи. А сейчас самое время их немного преобразовать, придать им чуть другой облик. Если говорить конкретно, то нужно перейти к комплексному представлению сигналов! Помните, на эту тему была отдельная статья? В ней я говорил, что она нужна для понимания некоторых моментов в дальнейших статьях. Вот как раз и наступил тот момент, когда пора вспомнить все эти хитрые мнимые единицы. Если говорить конкретно, то сейчас нам потребуется показательная запись комплексного числа. Как мы помним из статьи про комплексные числа в электротехнике, если у нас есть синусоидальный сигнал вида
то его можно представить в показательной форме вот так
Почему это так, откуда взялось, что здесь какая буковка значит – обо всем уже подробно говорили. Для повторения можно перейти по ссылке и еще раз со всем ознакомиться. Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого
Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике. Однако тогда я про него как-то позабыл, поэтому давайте рассмотрим его сейчас. Давайте представим, что t=0. Это приведет к исключению из расчетов времени и и частоты, и мы переходим к так называемым комплексным амплитудам сигнала. Безусловно, это не значит, что сигнал из переменного становится постоянным. Нет, он все так же продолжает изменяться по синусу с той же самой частотой. Но бывают моменты, когда частота нам не очень важна, и тогда лучше от нее избавиться и работать только с амплитудой сигнала. Сейчас как раз такой момент. Поэтому полагаем t=0 и получаем комплексную амплитуду напряжения
Давайте раскроем скобки в экспоненте и воспользуемся правилами работы с показательными функциями.
Итак, у нас имеется три множителя. Будем разбираться со всеми по порядку. Объединим первые два и запишем выражение следующего вида
Что мы вообще такое записали? Правильно, комплексную амплитуду тока через конденсатор. Теперь выражение для комплексной амплитуды напряжения принимает вид
Результат, к которому мы стремимся, уже близок, но остается еще один не очень приятный множитель с экспонентой. Как с ним быть? А, оказывается, очень просто. И снова нам на помощь придет статья по комплексным числам в электротехнике, не зря ж я ее писал
Да, вся эта хитрая экспонента с комплексными числами в показателе превращается всего лишь в мнимую единичку, перед которой стоит знак минус. Согласен, возможно, осознать это не так просто, но тем не менее математика говорит, что это так. Поэтому результирующая формула у нас принимает вид
Давайте выразим из этой формулы ток и приведем выражение к виду, соответствующему закону Ома. Получим
Как мы помним из статьи про закон Ома, у нас ток равнялся напряжению, деленному на сопротивление. Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение – переменные и представлены через комплексные амплитуды. Кроме того, не забываем, что ток течет у нас через конденсатор. Поэтому, выражение, которое стоит в знаменателе, можно рассматривать как емкостное сопротивление конденсатора переменному току:
Да, выражение для сопротивления конденсатора имеет вот такой вот вид. Оно, как вы можете заметить, комплексное. Об этом свидетельствует буковка j в знаменателе дроби. А что значит эта комплексность? На что она влияет и что показывает? А показывает она, господа, исключительно сдвиг фаз в 90 градусов между током и напряжением на конденсаторе. А именно, ток на 90 градусов опережает напряжение. Этот вывод не является для нас новостью, про все это было подробно рассказано в прошлой статье. Чтобы это лучше осознать, надо теперь мысленно пройтись от полученной формулы вверх к тому моменту, где у нас это j возникло. В процессе подъема вы увидите, что мнимая единица j возникло из формулы Эйлера из-за того, что там был компонент Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода? Да и вообще, пока лишь какие-то дико абстрактные буковки и нифига не ясно, как взять и оценить сопротивление какого-нибудь конкретно конденсатора, который мы купили в магазине и воткнули в схему. Давайте разбираться постепенно. Как мы уже говорили, буковка j в знаменателе говорит нам лишь о сдвиге фаз тока и напряжения. Но она не влияет на амплитуды тока и напряжения. Соответственно, если сдвиг фаз нас не интересует, то можно исключить эту буковку из рассмотрения и получить более простое выражение абсолютно без всяких комплексностей:
Согласитесь, жить стало чуточку легче. Это выражение позволяет рассчитать сопротивление конденсатора для конкретной емкость и частоты сигнала. Заметьте, господа, интересный факт. Сопротивление конденсатора, оказывается, зависит не только от самого конденсатора (а именно его емкости), но и от частоты протекающего тока. Если вспомнить обычные резисторы, то в них у нас сопротивление зависело только от самого резистора, материала, формы и всего такого прочего, но не зависело от частоты (разумеется, мы говорим сейчас про идеальные резисторы, без всяких паразитных параметров). Здесь все по-другому. Один и тот же конденсатор на разной частоте будет иметь разное сопротивление и через него будет течь ток разной амплитуды при одной и той же амплитуде напряжения. Что еще мы можем сказать, глядя на эту формулу? Например, то, что чем больше частота сигнала, тем меньше для него сопротивление конденсатора. И чем больше емкость конденсатора, тем меньше его сопротивление переменному току. По аналогии с резисторами, сопротивление конденсаторов измеряется все так же в Омах. Однако всегда следует помнить, что это немного другое сопротивление, его называют реактивным. И другое оно в первую очередь из-за того самого пресловутого j в знаменателе, то есть из-за сдвига фазы. У «обычных» (которые называют активными) Омов такого сдвига нет, там напряжение четко совпадает по фазе с током. Давайте построим график зависимости сопротивления конденсатора от частоты. Для определенности емкость конденсатора возьмем фиксированной, скажем, 1 мкФ. График представлен на рисунке 2.
Рисунок 2 (кликабельно) – Зависимость сопротивления конденсатора от частоты На рисунке 2 мы видим, что сопротивление конденсатора переменному току убывает по закону гиперболы. При стремлении частоты к нулю (то есть фактически при стремлении переменного току к постоянному) сопротивление конденсатора стремится к бесконечности. Это и логично: мы все помним, что для постоянного тока конденсатор фактически представляет собой разрыв цепи. На практике оно, конечно, не бесконечно, а ограничено сопротивлением утечки конденсатора. Тем не менее, оно все равно очень велико и часто его и считают бесконечно большим. При стремлении частоты к бесконечности, сопротивление конденсатора стремится к нулю. Это все в теории, конечно. На практике реальный конденсатор обладает рядом паразитных параметров (в частности, паразитная индуктивности и сопротивление утечки), из-за чего сопротивление уменьшается только лишь до некоторой определенной частоты, а потом начинает наоборот расти. Но об этом более подробно в другой раз. Есть еще один вопрос, который хотелось бы обговорить, прежде чем начинать рассмотрение примеров. Зачем вообще писать букву j в знаменателе сопротивления? Не достаточно ли просто всегда помнить про сдвиг фаз, а в записи использовать числа без этой мнимой единицы? Оказывается, нет. Представим себе цепь, где одновременно присутствуют резистор и конденсатор. Скажем, они соединены последовательно. И вот тут-то как раз мнимая единичка рядом с емкостью не позволит просто так взять и сложить активное и реактивное сопротивление в одно действительное число. Общее сопротивление такой цепочки будет комплексным, причем состоящим как из действительной части, так и из мнимой. Действительная часть будет обусловлена резистором (активными сопротивлением), а мнимая – емкостью (реактивным сопротивлением). Впрочем, это все тема для другой статьи, сейчас не будем в это углубляться. Давайте лучше перейдем к примерам. Пусть у нас есть конденсатор емкостью, скажем C=1 мкФ. Требуется определить его сопротивление на частоте f1=50 Гц и на частоте f2=1 кГц. Кроме того, следует определить амплитуду тока с учетом того, что амплитуда приложенного к конденсатору напряжения равна Um=50 В. Ну и построить графики напряжения и тока. Собственно, задачка эта элементарная. Подставляем циферки в формулу для сопротивления и получаем для частоты f1=50 Гц сопротивление, равное
А для частоты f2=1 кГц сопротивление будет
По закону Ома находим величину амплитуды тока для частоты f1=50 Гц
Аналогично для второй частоты f2=1 кГц
Теперь мы легко можем записать законы изменения тока и напряжения, а также построить графики для этих двух случаев. Полагаем, что напряжение у нас изменяется по закону синуса для первой частоты f1=50 Гц следующим образом
А для второй частоты f2=1 кГц вот так
Дальше мы помним, что ток в конденсаторе опережает напряжение на
и для частоты f2=1 кГц
Графики тока и напряжения для частоты f1=50 Гц представлены на рисунке 3
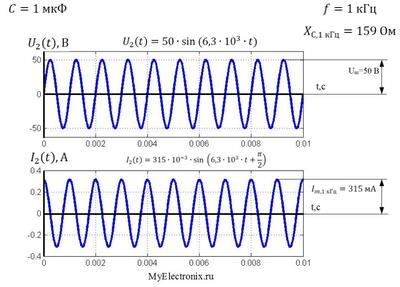
Рисунок 3 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f1=50 Гц Графики тока и напряжения для частоты f2=1 кГц представлены на рисунке 4
Рисунок 4 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f2=1 кГц Итак, господа, мы сегодня познакомились с таким понятием, как сопротивление конденсатора переменному току, научились его считать и закрепили полученные знания парочкой примеров. На сегодня все. Спасибо что прочитали, всем огромной удачи и пока!
Вступайте в нашу группу Вконтакте Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it. myelectronix.ru Электрический конденсатор. Виды конденсаторов.Много написано про конденсаторы, стоит ли добавлять еще пару тысяч слов к тем миллионам, что уже есть? Таки добавлю! Верю, что моё изложение принесёт пользу. Ведь оно будет сделано с учётом целей этого сайта.
Что такое электрический конденсаторЕсли говорить по-русски, то конденсатор можно обозвать "накопитель". Так даже понятнее. Тем более именно так переводится на наш язык это название. Стакан тоже можно обозвать конденсатором. Только он накапливает в себе жидкость. Или мешок. Да, мешок. Оказывается тоже накопитель. Накапливает в себе всё, что мы туда засунем. Причем тут электрический кондесатор? Он такой же как стакан или мешок, но только накапливает электрический заряд. Представь себе картину: по цепи проходит электрический ток, на его пути встречаются резисторы, проводники и, бац, возник конденсатор (стакан). Что случится? Как ты знаешь, ток -- это поток электронов, а каждый электрон имеет электрический заряд. Таким образом, когда кто-то говорит, что по цепи проходит ток, ты предствляешь себе как по цепи бегут миллионы электронов. Именно вот эти самые электрончики, когда на их пути возникает конденсатор, и накапливаются. Чем больше запихнем в конденсатор электронов, тем больше будет его заряд. Возникает вопрос, а сколько можно таким образом накопить электронов, сколько влезет в конденсатор и когда он "наестся"? Давай выяснять. Очень часто для упрощенного объяснения простых электрических процессов используют сравнение с водой и трубами. Воспользуемся таким подходом тоже. Представь, трубу, по которой течет вода. На одном конце трубы насос, который с силой закачивает воду в эту трубу. Затем поперек трубы мысленно поставь резиновую мембрану. Что произойдёт? Мембрана станет растягиваться и напрягаться под действием силы давления воды в трубе (давление создаётся насосом). Она будет растягиваться, растягиваться, растягиваться и в итоге сила упругости мембраны либо уравновесит силу насоса и поток воды остановится, либо мембрана порвётся (Если так непонятно, то представь себе воздушный шарик, который лопнет, если его накачать слишком сильно)! Тоже самое происходит и в электрических конденсаторах. Только там вместо мембраны используется электрическое поле, которое растёт по мере зарядки конденсатора и постепенно уравновешивает напряжение источника питания. Таким образом, у конденсатора есть некоторый предельный заряд, который он может накопить и после превышения которого произойдёт пробой диэлектрика в конденсаторе он сломается и перестанет быть конденсатором. Самое время, видимо, рассказать как устроен конденсатор. Как устроен электрический конденсаторВ школе тебе рассказывали, что конденсатор -- это такая штуковина, которая состоит из двух пластин и пустоты между ними. Пластины эти называли обкладками конденсатора и к ним подключали проводки, чтобы подать напряжение на конденсатор. Так вот современные конденсаторы не сильно отличаются. Они все также имеют обкладки и между обкладками находится диэлектрик. Благодаря наличию диэлектрика улучшаются харктеристики конденсатора. Например, его ёмкость. В современных конденсаторах используются разные виды диэлектриков (об этом ниже), которые запихиваются между обкладок конденсаторов самыми изощренными способами для достижения опредлённых характеристик. Принцип работыОбщий принцип работы достаточно прост: подали напряжение -- заряд накопился. Физические процессы, которые при этом происходят сейчас тебя не сильно должны интересовать, но если захочешь, то можешь об этом прочитать в любой книге по физике в разделе электростатики. Конденсатор в цепи постоянного тока Если поместить наш конденсатор в электрическую цепь (рис. ниже), включить последовательно с ним амперметр и подать в цепь постоянный ток, то стрелка амперметра кратковременно дёрнется, а затем замрет и будет показывать 0А -- отсутствие тока в цепи. Что случилось? Будем считать, что до того, как был подан ток в цепь, конденсатор был пуст (разряжен), а когда подали ток, то он очень быстро стал заряжаться, а когда зарядился (эл. поле между обкладками конденсатора уравновесило источник питания), то ток прекратился (здесь график заряда конденсатора). Именно поэтому говорят, что конденсатор не пропускает постоянный ток. На самом деле пропускает, но очень короткое время, которое можно посчитать по формуле t = 3*R*C (Время зарядки конденсатора до объёма 95% от номинального. R- сопротивление цепи, C - ёмкость конденсатора) Так конденсатор ведёт себя в цепи постоянного тока. Совсем иначе он себя ведёт в цепи переменного! Конденсатор в цепи переменного тока Что такое переменный ток? Это когда электроны "бегут" сначала туда, потом назад. Т.е. направление их движения все время меняется. Тогда, если по цепи с конденсатором побежит переменный ток, то на каждой его обкладке будет скапливаться то "+" заряд, то "-". Т.е. фактически будет протекать переменный ток. А это значит, что переменный ток "беспрепятственно" проходит через конденсатор. Весь этот процесс можно смоделировать с помощью метода гидравлических аналогий. На картинке ниже аналог цепи переменного тока. Поршень толкает жидкость то вперёд, то назад. Это заставляет крутится крыльчатку вперёд-назад. Получается как бы переменный поток жидкости (читаем переменный ток). Давай теперь поместим между источником силы (поршнем) и крыльчаткой меодель конденсатора в виде мембраны и проанализируем, что изменится. Похоже, что ничего не изменится. Как жидкость совершала колебательные движения, так она их и совершает, как из-за этого колебалась крыльчатка, так и будет колебаться. А значит наша мембрана не является препятствием для переменного потока. Также будет и для электронного конденсатора. Дело в том, что хоть электроны, которые бегут поцепи и не пересекают диэлектрик (мембрану) между обкладками конденсатора, но за пределами конденсатора их движение колебательное (туда-сюда), т.е. протекает переменный ток. Эх! Таким образом конденсатор пропускает переменный ток и задерживает постоянный. Это очень удобно, когда требуется убрать постоянную составляющую в сигнале, например, на выходе/входе аудиоусилителя или, когда требуется посмотреть только переменную часть сигнала (пульсации на выходе источника постоянного напряжения).
Реактивное сопротивление конденсатораКонденсатор обладает сопротивлением! В принципе, это можно было предположить уже из того, что через него не проходит постоянный ток, как если бы это был резистор с оооочень большим сопротивлением. Другое дело ток переменный -- он проходит, но испытывает со стороны конденсатора сопротивление: f - частота, С - ёмкость конденсатора. Если внимательно посмотреть на формулу, то станет видно, что если ток постоянный, то f = 0 и тогда (да простят меня воинствующие математики!) Xc = бесконечность.И постоянного тока через конденсатор нет. А вот сопротивление переменному току будет менять в зависимости от его частоты и ёмкости конденсатора. Чем больше частота тока и емкость конденсатора, тем меньше сопротивляется он этому току и наоборот. Чем быстрее меняется напряже-напряжение, тем больше ток через конденсатор, этим и объясняется уменьшение Хс с ростом частоты. Кстати, ещё одной особенность конденсатора заключается в том, что на нём не выделяется мощность, он не нагревается! Поэтому его иногда используют для гашения напряжения там, где резистор бы задымился. Например для понижения напряжения сети с 220В до 127В. И ещё: Ток в конденсаторе пропорционален скорости приложенного к его выводам напряжения Где используются конденсаторыДа везде где требуются их свойства (не пропускать постоянный ток, умение накапливать электрическую энергию и менять свое сопротивление в зависимости от частоты), в фильтрах, в колебательных контурах, в умножителях напряжения и т.д. Какие бывают конденсаторыПромышленность выпускает множество разных видов конденсаторов. Каждый из них обладает опредлёнными преимуществами и недостатками. У одних малый ток утечки, у других большая ёмкость, у третьих что-нибудь ещё. В зависимости от этих показателей и выбирают конденсаторы. Радиолюбители, особенно как мы -- начинающие -- особо не заморачиваются и ставят, что найдут. Тем не менее следует знать какие основные виды конденсаторов существуют в природе.
На картинке показано весьма условное разделение конденсаторов. Я его составил на свой вкус и нравится оно мне тем, что сразу понятно существуют ли переменные конденсаторы, какие бывают постоянные конденсаторы и какие диэлектрики используются в распространённых конденсаторах. В общем-то всё, что нужно радиолюбителю. Керамические конденсаторы Обладают малым током утечки, малыми габаритами, малой индуктивность, способны работать на высоких частотах и в цепях постоянного, пульсирующего и переменного тока. Выпускаются в широком диапазоне рабоичх напряжений и ёмкостей: от 2 до 20 000 пФ и в зависимости от исполнения выдерживают напряжение до 30кВ. Но чаще всего ты встретишь керамические конденсаторы с рабочим напряжением до 50В. Слюдяные конденсаторы Честно скажу не знаю выпускают ли их сейчас. Но раньше в таких конденсаторах в качестве диэлектрика использовалась слюда. А сам конденсатор состоял из пачки слюдяных, на каждой из которых с обеих сторон наносились обкладки, а потом такие платсинки собирались в "пакет" и запаковывались в корпус. Обычно они имели ёмкость от нескольких тысяч до десятков тысяч пикофорад и работали в диапазоне напряжений от 200 В до 1500 В. Бумажные конденсаторы Такие конденсаторы в качестве диэлектрика имеют конденсаторную бумагу, а в качестве обкладок -- алюминиевые полоски. Длинные ленты алюминиевой фольги с проложенной между ними лентой бумаги сворачиваются в рулон и пакуются в корпус. Вот и весь фокус. Такие конденсаторы бывают ёмкостью от тысяч пикофорад до 30 микрофорад, и могут выдерживать напряжение от 160 до 1500 В. Поговаривают, что сейчас они ценятся аудиофиалами. Не удивлен -- у них и провода односторонней проводимости бывают... Полиэстеровые конденсаторы В принципе обычные кондесаторы с полиэстером в качестве диэлектрика. Разброс ёмкостей от 1 нФ до 15 мФ при рабочем напряжении от 50 В до 1500 В. Полипропиленовые конденсаторы У конденсаторов этого типа есть два неоспоримых преимущества. Первое -- можно их делать с очень маленьким допуском всего в 1%. Так что, если на таком написано 100 пФ, то значит его ёмкость 100 пФ +/- 1%. И второе -- это то, что их рабочее напряжение может достигать до 3 кВ (а ёмкость от 100 пФ, до 10 мФ) Электролитические кондесаторы Эти конденсаторы отличаются от всех других тем, что их можно включать только цепь постоянного или пульсирующего тока. Они полярные. Имеют плюс и минус. Связано это с их конструкцией. И если такой конденсатор включить наоборот, то он скорее всего вздуется. А раньше они еще и весело, но небезопасно взрывались. Бывают электролитические конденсаторы алюминиевые и танталовые. Алюминиевые электролитические конденсаторы устроены почти как бумажные с той лишь разницей, что обкладками такого конденсатора являются бумажная и алюминиевые полосы. Бумага пропитана электролитом, а на алюминиевыую полосу нанесен тонкий слой окисла, который и выступает в роли диэлектрика. Если подать на такой конденсатор переменный ток или включить обратно полярностям вывода, то электролит закипает и конденсатор выходит из строя. Танталовые отличаются от алюминиевых тем что: в качестве диэлектрика используется пентаоксид тантала, меют рабочее напряжение до 100 В, имеют малые габариты, меньшую паразитная индуктивность (что позволяет их использовать в высокочастотных цепях). Электролитические конденсаторы обладают достаточно большой ёмкостью, благодаря чему их, к примеру, часто используют в выпрямительных цепях. На этом наверно всё. За кадром остались конденсаторы с диэлектриком из полкарбоната, полистирола и наверно ещё многие другие виды. Но думаю, что это уже будет лишним. Продолжение следует...Во второй части я планирую показать примеры типичного использования конденсаторов. Так что жми ctrl+D и добавляй mp16.ru к себе в закладки, что бы не потерять. Что еще почитать mp16.ru Цепь переменного тока с конденсаторомПри переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости, через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток).Токи проводимости и поляризацию диэлектрика сопровождают потери энергии. Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами. Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(P = 0). Схема замещения конденсатора с параллельным соединением элементовРеальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной Bс проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе G = Р/Uc2, а емкость — конструкцией конденсатора. Предположим, что проводимости G и Вс для такой цепи известны, а напряжение имеет уравнение u = Umsinωt. Требуется определить токи в цепи и мощность. i = iG + ic, (13.30) Учитывая, что ток iG совпадает по фазе с напряжением, а ток ic опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:
Векторная диаграмма токов в цепи с конденсаторомДля определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению I = IG + IC
Действующие величины составляющих тока:
IG = GU (13.31)
IC = BCU (13.32) Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φa =0). Вектор IG совпадает по направлению с вектором U, а вектор IC направлен перпендикулярно вектору U с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90º. Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC : i = Imsin(ωt + φ)
Треугольник проводимостей для конденсатораСтороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная G = IG/U и емкостная Вс = Iс/U проводимости, а гипотенузой — полная проводимость цепи Y = I/U. Из треугольника проводимостей
Связь между действующими величинами напряжения и тока выражается формулами I = UY
U = I/Y (13.35)
Из треугольников токов и проводимостей определяют величины
cosφ = IG/I = G/Y; sinφ = Ic/I = Bc/Y; tgφ = IC/IG = Bc/G. (13.36)
Мощность цепи с конденсаторомВыражение мгновенной мощности реального конденсатора p = ui = Umsinωt * Imsin(ωt+φ) совпадает с выражением мгновенной мощности катушки. Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17. Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19) — (13.22)]. Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U. В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности; активная P = UIG = UIcosφ реактивная Q = UIC = UIsinφ полная
Схема замещения конденсатора с последовательным соединением элементовРеальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Хс сопротивлениями. На рис. 13.18, а такая схема показана в сравнении со схемой параллельного electrikam.com Конденсатор в цепи переменного тока     «Физика - 11 класс» Постоянный ток не может идти по цепи, содержащей конденсатор, так как обкладки конденсатора разделены диэлектриком. Переменный же ток может идти по цепи, содержащей конденсатор. Есть источники постоянного и переменного напряжений, в которых постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. Цепь состоит из конденсатора и лампы накаливания, соединенных последовательно. При включении постоянного напряжения (переключатель влево) лампа не светится. При включении переменного напряжения (переключатель вправо) лампа загорается, если емкость конденсатора достаточно велика. Под действием переменного напряжения происходит периодическая зарядка и разрядка конденсатора. Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы. Если сопротивлением проводов и обкладок конденсатора можно пренебречь, то напряжение на конденсаторе равно напряжению на концах цепи. Следовательно, Заряд конденсатора меняется по гармоническому закону: q = CUm cos ωt Сила тока, представляющая собой производную заряда по времени, равна: Колебания силы тока опережают по фазе колебания напряжения на конденсаторе на . Амплитуда силы тока равна: Im = UmCω Если ввести обозначение и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим Величину Хс, обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением.Роль этой величины аналогична роли активного сопротивления R в законе Ома. Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.Это и позволяет рассматривать величину Хс как сопротивление конденсатора переменному току (емкостное сопротивление). Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Хс. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты ω. На протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля.В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть. Итак,сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на . Источник: «Физика - 11 класс», учебник Мякишев, Буховцев, Чаругин Электромагнитные колебания. Физика, учебник для 11 класса - Класс!ная физика Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях --- Аналогия между механическими и электромагнитными колебаниями --- Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний --- Переменный электрический ток --- Активное сопротивление. Действующие значения силы тока и напряжения --- Конденсатор в цепи переменного тока --- Катушка индуктивности в цепи переменного тока --- Резонанс в электрической цепи --- Генератор на транзисторе. Автоколебания --- Краткие итоги главы Устали? - Отдыхаем!  Вверх class-fizika.ru
electric-220.ru Конденсатор в цепи переменного и постоянного токаЕсли конденсатор присутствует в цепи постоянного тока, то возникающий кратковременный импульс производит его зарядку до значения напряжения источника, после чего движение тока прекращается. Отключенный от источника тока, заряженный конденсатор под действием нагрузки будет очень быстро разряжаться. Его разрядка напоминает кратковременный импульс. При этом, лампа накаливания мигнет один раз и погаснет. Использование конденсатораКонденсатор в цепи переменного тока ведет себя совершенно иначе. Зарядка и разрядка чередуется с периодами колебаний переменного напряжения. Находящаяся в цепи лампа накаливания, соединенная последовательно, как и конденсатор будет визуально излучать непрерывный свет, поскольку промышленная частота колебаний не заметна для человеческого глаза. Каждый конденсатор обладает емкостным сопротивлением, которое находится в обратной пропорциональной зависимости от его емкости и частоты циклов переменного тока. При таком сопротивлении, электрическая и магнитная энергия не превращается в тепловую. Таким образом, чем выше частота тока, тем ниже значение емкостного сопротивления и наоборот. На основании этого важного свойства, конденсатор нашел практическое применение в цепях переменного тока, как гасящий элемент в делителях напряжения вместо резисторов. Это особенно актуально при значительном падении напряжения. В этом случае потребовались бы резисторы с большой мощностью и габаритами. Конденсатор в цепи переменного тока не нагревается, поэтому и не происходит рассеивания энергии. Это связано со смещением напряжения и тока в конденсаторе между собой на 90 градусов. При максимальном напряжении ток равен нулю, при этом, мощность также равна нулю. Значит, никакой работы не совершается, и нагрев отсутствует. Конденсатор вместо резистораЭто является основной причиной применения во многих случаях, конденсаторов вместо резисторов. Однако, при таком использовании, у конденсатора есть существенный недостаток, который нужно обязательно учитывать. В том случае, когда переменный ток в цепи изменяется, происходит изменение напряжения у нагрузки. Другой недостаток наблюдается, когда отсутствует гальваническая развязка. Поэтому, в целом, конденсаторы, как гасящие элементы, применяются достаточно ограничено. Они используются при относительно стабильном сопротивлении нагрузки. В качестве примера можно привести цепи питания в нагревательных элементах. Тем не менее, конденсаторы нашли достаточно широкое применение при создании различных частотных фильтров и некоторых видов резонансных схем. electric-220.ru Поведение конденсатора в цепи переменного токаЕсли говорить строго, то через конденсатор не проходит ни постоянный, ни переменный ток, так как между обкладками находится изолятор, в котором свободные электрические заряды двигаться не могут. Включение конденсатора в цепь постоянного тока равносильно разрыву этой цепи. Что же касается переменного тока, то он будет протекать по цепи, в которую включен конденсатор, благодаря периодическому заряду и разряду этого конденсатора. Действительно, когда происходит заряд конденсатора, то электрические заряды, например электроны, на одной обкладке накапливаются, а с другой обкладки уходят. При этом они, конечно, двигаются по соединительным проводам, подключенным к обкладкам конденсатора. Такое же движение зарядов, только в противоположном направлении, происходит и при разряде конденсатора. Если включить конденсатор в цепь переменного тока, то он будет периодически заряжаться то в одной полярности, то в противоположной. Это значит, что электроны будут накапливаться то на одной, то на другой обкладке, и каждый раз при заряде и разряде свободные электроны будут двигаться по цепи, в которую включен конденсатор, не попадая, однако, в изолятор, включенный между обкладками. А поскольку под действием переменного напряжения в цепи конденсатора двигаются заряды, то мы считаем, что конденсатор пропускает переменный ток, хотя и в этом случае заряды не проходят через изолятор. Конденсатор влияет на величину переменного тока в цепи, и поэтому (по аналогии с законом Ома) его часто рассматривают как сопротивление. Это так называемое емкостное сопротивление обозначается буквой хс и так же, как и обычное сопротивление, измеряется в омах. Величина хс зависит от частоты переменного тока и от емкости С конденсатора: с уменьшением емкости конденсатора, так же как и с уменьшением частоты переменного тока, емкостное сопротивление конденсатора увеличивается (рис. 80, 81, лист 87). Эту зависимость удобно записать в виде простой формулы:
Смысл этой формулы весьма прост: чем меньше емкость С, тем меньше зарядов будет двигаться к обкладкам при каждом заряде и разряде конденсатора; чем меньше частота переменного тока, тем реже будет заряжаться и разряжаться конденсатор. Отсюда следует, что с уменьшением f и С уменьшается ток в цепи, или, иными словами, растет сопротивление конденсатора. Этот вывод имеет огромное практическое значение. Так, например, если нам понадобится включить в цепь конденсатор с очень маленьким емкостным сопротивлением, то емкость этого конденсатора нужно будет выбирать с учетом частоты переменного тока в цепи. Для высоких частот можно будет взять конденсатор небольшой емкости, а вот для низких частот емкость конденсатора придется взять большой. Это хорошо иллюстрируется простым примером. На частоте 100 кгц конденсатор емкостью 100 пф обладает емкостным сопротивлением хс=16 ком. При уменьшении частоты в 1000 раз, то есть на частоте 100 гц, сопротивление конденсатора возрастет в 1000 раз и станет равным 16 000 ком (16 Мом). Для того чтобы при уменьшении частоты емкостное сопротивление не изменилось, нужно увеличить емкость конденсатора. Сопротивление 16 ком на частоте 100 гц будет иметь конденсатор емкостью 100 000 пф (0,1 мкф). Из приведенной выше формулы следует также, что уменьшение емкости конденсатора связи Ссв (лист 85) приведет к росту сопротивления этого конденсатора, а следовательно, к уменьшению тока в цепи антенны. Поэтому емкость Ссв нельзя брать слишком малой. Сказанное можно пояснить еще иначе. Конденсатор связи и колебательный контур Lк Ск можно рассматривать как делитель напряжения, к которому приложена э. д. с, действующая между зажимами А («антенна») и З («земля»). Мы не будем пока говорить о том, чему равно сопротивление колебательного контура - даже без этого ясно: чем больше емкостное сопротивление конденсатора связи, тем меньшая часть э. д. с. будет действовать на нижней части делителя - на контуре и подключенной к нему цепи детектор - телефон. oldradiogid.ru |
|
||||||||||||||||||
|
|
||||||||||||||||||
|




 . При проектировании схем этот момент обязательно надо иметь в виду. Согласитесь, господа, крайне неприятно поставить в схему конденсатор и потом столкнуться с тем, что из-за высокой частоты он ведет себя и не как конденсатор вовсе, а как самый настоящий дроссель. Это, безусловно, очень важная тема, но сегодня речь пойдет не о ней. В сегодняшней статье мы будем говорить непосредственно про емкостное сопротивление конденсатора. То есть мы будем считать его идеальным, без каких бы то ни было паразитных параметров вроде индуктивности или активного сопротивления.
. При проектировании схем этот момент обязательно надо иметь в виду. Согласитесь, господа, крайне неприятно поставить в схему конденсатор и потом столкнуться с тем, что из-за высокой частоты он ведет себя и не как конденсатор вовсе, а как самый настоящий дроссель. Это, безусловно, очень важная тема, но сегодня речь пойдет не о ней. В сегодняшней статье мы будем говорить непосредственно про емкостное сопротивление конденсатора. То есть мы будем считать его идеальным, без каких бы то ни было паразитных параметров вроде индуктивности или активного сопротивления.

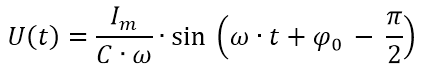

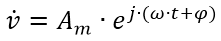





 . Давайте преобразуем этот множитель, воспользовавшись формулой Эйлера:
. Давайте преобразуем этот множитель, воспользовавшись формулой Эйлера:



 . Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло.
. Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло.










 Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них так же синусоидальны. При параллельном соединении ветвей G и Вс , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:
Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них так же синусоидальны. При параллельном соединении ветвей G и Вс , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:
 При напряжении u = Umsinωt соответствии с векторной диаграммой уравнение тока
При напряжении u = Umsinωt соответствии с векторной диаграммой уравнение тока

 соединения активной и емкостной проводимостей (рис.13. 18,6). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным. Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью С[BC = ωC, Xc = 1/(ωC)] Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а. Если вам интересно прочитайте статью о настоящих конденсаторах которые применяются в промышленности.
соединения активной и емкостной проводимостей (рис.13. 18,6). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным. Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью С[BC = ωC, Xc = 1/(ωC)] Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а. Если вам интересно прочитайте статью о настоящих конденсаторах которые применяются в промышленности.









