Конденсатор и переменный ток: Конденсатор в цепи переменного тока: как работает, формулы, схема

Конденсаторы и цепи переменного тока . Искусство схемотехники. Том 1 [Изд.4-е]

Коль скоро мы начинаем рассматривать изменяющиеся сигналы напряжения и тока, нам необходимо познакомиться с двумя очень занятными элементами, которые не находят применения в цепях постоянного тока, — речь идет о конденсаторах и индуктивностях. Скоро вы убедитесь, что эти компоненты вместе с резисторами являются основными элементами пассивных линейных цепей, составляющих основу почти всей схемотехники.

Особенно следует подчеркнуть роль конденсаторов — без них не обходится почти ни одна схема. Они используются при генерации колебаний, в схемах фильтров, для блокировки и шунтирования сигналов. Их используют в интегрирующих и дифференцирующих схемах. На основе конденсаторов и индуктивностей строят схемы формирующих фильтров для выделения нужных сигналов из фона.

Некоторые примеры подобных схем вы найдете в этой главе, а еще большее число интересных примеров использования конденсаторов и индуктивностей встретится вам в последующих главах.

Приступим к более детальному изучению конденсаторов. Явления, протекающие в конденсаторе, описываются математическими зависимостями, поэтому читателям, которые имеют недостаточную подготовку в области математики, полезно прочитать приложение Б. Не огорчайтесь, если некоторые детали не будут сразу вполне понятны, главное — это общее понимание вопроса.

1.12. Конденсаторы

Конденсатор (рис. 1.27) — это устройство, имеющее два вывода и обладающее следующим свойством:

Q = CU.

Рис. 1.27. Конденсатор.

Конденсатор, имеющий емкость С фарад, к которому приложено напряжение U вольт, накапливает заряд Q кулон на одной пластине и —Q — на другой.

В первом приближении конденсаторы — это частотно-зависимые резисторы. Они позволяют создавать, например, частотно-зависимые делители напряжения.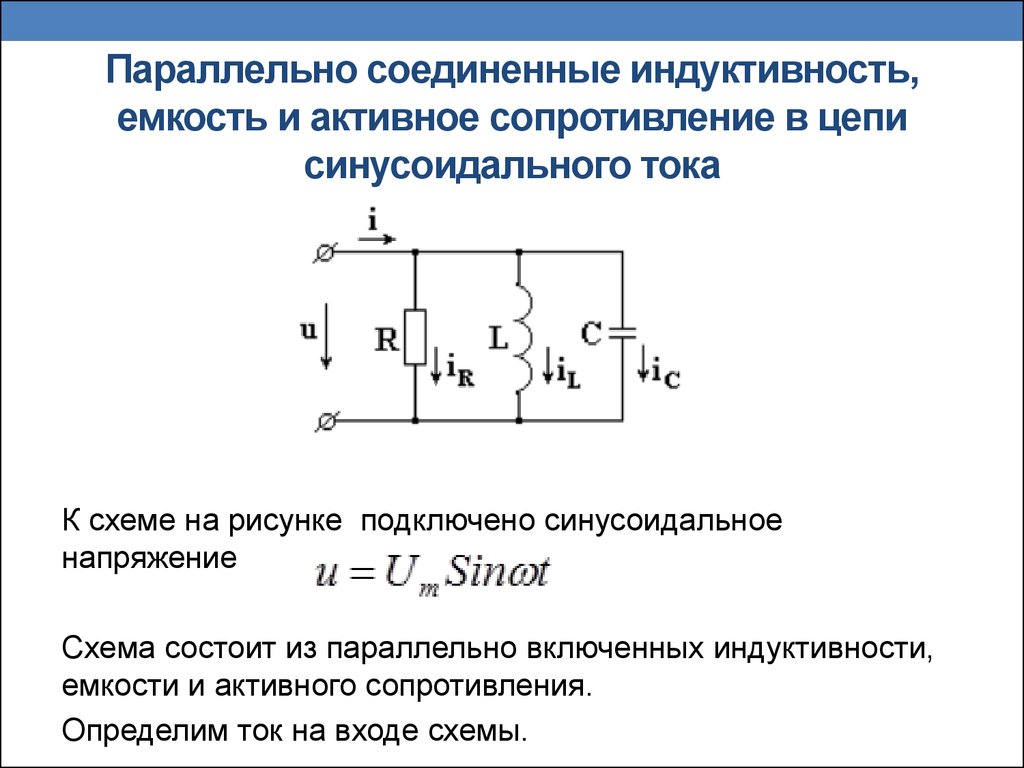 Для решения некоторых задач (шунтирование, связывание контуров) больших знаний о конденсаторе и не требуется, другие задачи (построение фильтров, резонансных схем, накопление энергии) требуют более глубоких знаний. Например, конденсаторы не рассеивают энергию, хотя через них и протекает ток, — дело в том, что ток и напряжение на конденсаторе смещены друг относительно друга по фазе на 90°.

Продифференцировав выражение для Q (см. приложение Б), получим

I = C(dU/dt).

Итак, конденсатор — это более сложный элемент, чем резистор; ток пропорционален не просто напряжению: а скорости изменения напряжения. Если напряжение на конденсаторе, имеющем емкость 1 Ф, изменится на 1 В за 1 с, то получим ток 1 А. И наоборот, протекание тока 1 А через конденсатор емкостью 1 Φ вызывает изменение напряжения на 1 В за 1 с.

Емкость, равная одной фараде, очень велика, и поэтому чаще имеют дело с микрофарадами (мкФ) или пикофарадами (пФ). Для того чтобы сбить с толку непосвященных, на принципиальных схемах иногда опускают обозначения единиц измерения. Их приходится угадывать из контекста. Например, если подать ток 1 мА на конденсатор емкостью 1 мкФ, то напряжение за 1 с возрастет на 1000 В.

Импульс тока продолжительностью 10 мс вызовет увеличение напряжения на конденсаторе на 10 В (рис. 1.28).

Рис. 1.28. Напряжение на конденсаторе изменяется, когда через него протекает ток.

Промышленность выпускает конденсаторы разнообразных форм и размеров, через некоторое время вы познакомитесь с наиболее распространенными представителями этого обширного семейства.

Простейший конденсатор состоит из двух проводников, расположенных на небольшом расстоянии друг от друга (но не соприкасающихся между собой), настоящие простейшие конденсаторы имеют именно такую конструкцию. Чтобы получить большую емкость, нужны большая площадь и меньший зазор между проводниками, обычно для этого один из проводников покрывают тонким слоем изолирующего материала (называемого диэлектриком), для таких конденсаторов используют, например, алитированную (покрытую алюминием) майларовую пленку.

Широкое распространение получили следующие типы конденсаторов: керамические, электролитические (изготовленные из металлической фольги с оксидной пленкой в качестве изолятора), слюдяные (изготовленные из металлизированной слюды). Каждому типу конденсаторов присущи свои качества, краткий перечень отличительных особенностей каждого типа конденсаторов приведен мелким шрифтом в разделе «Конденсаторы». В общем можно сказать, что для некритичных схем подходят керамические и майларовые конденсаторы, в схемах, где требуется большая емкость, применяются танталовые конденсаторы, а для фильтрации в источниках питания используют электролитические конденсаторы.

Параллельное и последовательное соединение конденсаторов. Емкость нескольких параллельно соединенных конденсаторов равна сумме их емкостей. Нетрудно в этом убедиться: приложим напряжение к параллельному соединению, тогда

CU = Q = Q₁ + Q₂ + Q₃ +… =

= C₁U + C₂U + C₃U +…=

= (C₁ + C₂ + C₃ +…)·U =

или

С = С₁ + С₂ + С₃ +….

Для последовательного соединения конденсаторов имеем такое же выражение, как для параллельного соединения резисторов:

В частном случае для двух конденсаторов:

С = С₁С₂/(С₁ + С₂).

Ток, заряжающий конденсатор (I = C·dU/dt), обладает некоторыми особыми свойствами. В отличие от тока, протекающего через резистор, он пропорционален не напряжению, а скорости изменения напряжения (т. е. его производной по времени). Далее, мощность (U умноженное на I), которая связана с протекающим через конденсатор током, не обращается в тепло, а сохраняется в виде энергии внутреннего электрического поля в конденсаторе. При разряде конденсатора происходит извлечение энергии. Эти занятные свойства мы рассмотрим с другой точки зрения, когда будем изучать реактивность (начиная с разд.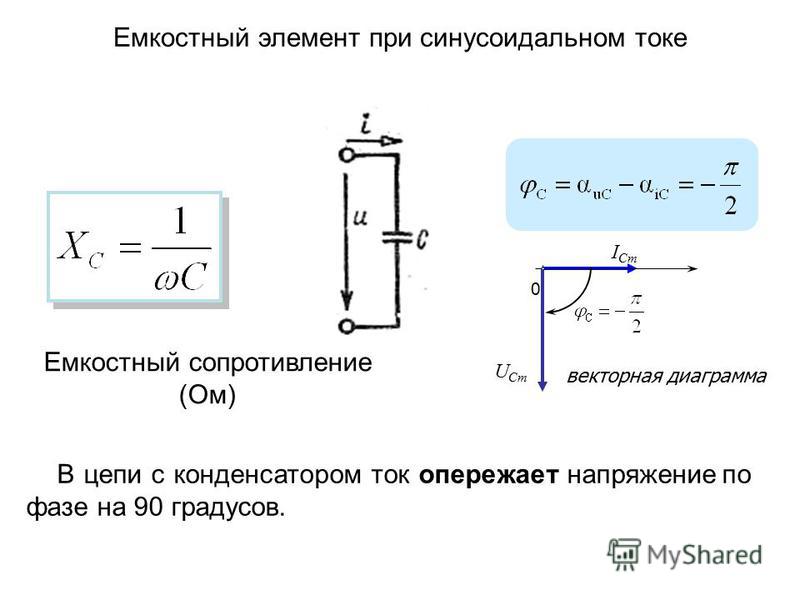 1.18).

* * *

КОНДЕНСАТОРЫ

Промышленностью выпускается много типов конденсаторов. Здесь перечислены основные преимущества и недостатки различных типов. Очевидно, что данная оценка имеет несколько субъективный характер (см. таблицу).

_{Упражнение 1.12. Получите выражение для емкости двух последовательно соединенных конденсаторов.}

_{Подсказка: так как точка соединения конденсаторов не имеет внешних подключений, то заряд, накопленный двумя конденсаторами, должен быть одинаков.}

* * *

1.13. RС-цепи: изменения во времени напряжения и тока

Для анализа цепей переменного тока (или в общем случае схем, работающих с изменяющимися напряжениями и токами) можно использовать характеристики двух типов. Во-первых, можно рассматривать изменения напряжения U и тока I во времени, а во-вторых, — изменение амплитуды при изменении частоты сигнала. И те, и другие характеристики имеют свои преимущества, и в каждом практическом случае приходится выбирать наиболее подходящие. Мы начнем изучение цепей переменного тока с временных зависимостей, а в разд. 1.18 перейдем к частотным характеристикам.

Каковы же свойства схем, в состав которых входят конденсаторы? Для того чтобы ответить на этот вопрос, рассмотрим простейшую RС-цепь (рис. 1.29).

Рис. 1.29.

Воспользуемся полученным ранее выражением для емкости:

C(dU/dt) = I = — U/R.

Это выражение представляет собой дифференциальное уравнение, решение которого имеет вид

U = A·e^-t/RC.

Отсюда следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на рис.  1.30.

Рис. 1.30. Сигнал разряда RС-цепи.

Постоянная времени. Произведение RC называют постоянной времени цепи. Если R измерять в омах, а С — в фарадах, то произведение RC будет измеряться в секундах. Для конденсатора емкостью 1 мкФ, подключенного к резистору сопротивлением 1 кОм, постоянная времени составляет 1 мс, если конденсатор был предварительно заряжен и напряжение на нем составляет 1 В, то при подключении резистора в цепи появится ток, равный 1 мА.

На рис. 1.31 показана несколько иная схема.

Рис. 1.31.

В момент времени t = 0 схема подключается к батарее. Уравнение, описывающее работу такой схемы, выглядит следующим образом:

I = C(dU/dt) = (U_вх — U)/R

и имеет решение

U = U_вх + Ae^-t/RC.

Не пугайтесь, если не поняли, как выполнено математическое преобразование. Важно запомнить полученный результат. В дальнейшем мы будем многократно его использовать, не прибегая к математическим выкладкам. Постоянная величина А определяется из начальных условий (рис. 1.32): U = 0 при I = 0, откуда А = — U_вх и U = U_вх(1 — e^-t/RC).

Рис. 1.32.

Установление равновесия. При условии t >> RC напряжение достигает значения U_вх. (Советуем запомнить хорошее практическое правило, называемое правилом пяти RC. Оно гласит: за время, равное пяти постоянным времени, конденсатор заряжается или разряжается на 99 %.) Если затем изменить входное напряжение U_вх (сделать его равным, например, нулю), то напряжение на конденсаторе U будет убывать, стремясь к новому значению по экспоненциальному закону e^-t/RC.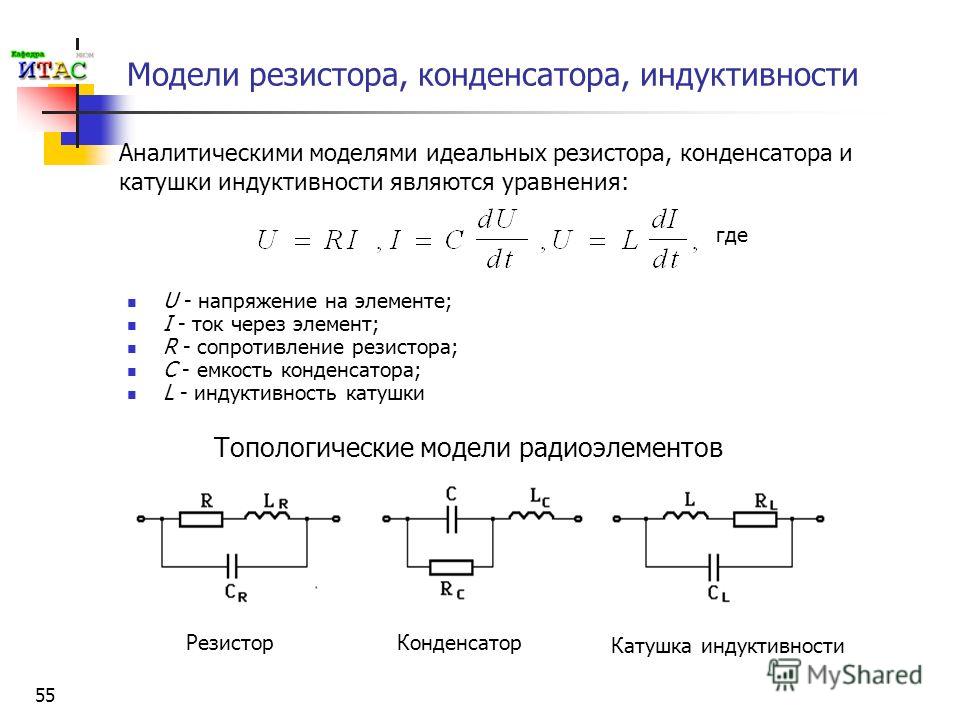

Например, если на вход подать прямоугольный сигнал U_вх, то сигнал на выходе U будет иметь форму, показанную на рис. 1.33.

Рис. 1.33. Напряжение, снимаемое с конденсатора (верхние сигналы), при условии, что на него через резистор подается прямоугольный сигнал.

_{Упражнение 1.13. Докажите, что время нарастания сигнала (время, в течение которого сигнал изменяется от 10 до 90 % своего максимального значения) составляет 2,2RC.}

У вас, наверное, возник вопрос: каков закон изменения для произвольного U_вх(t)? Для того чтобы ответить на него, нужно решить неоднородное дифференциальное уравнение (стандартные методы решения таких уравнений здесь не рассматриваются). В результате получим

Согласно полученному выражению, RC— цепь усредняет входное напряжение с коэффициентом пропорциональности e^-Δt/RC, где Δt = τ — t_^. На практике, однако, такой вопрос возникает редко. Чаще всего рассматриваются частотные характеристики и определяют, какие изменения претерпевает каждая частотная составляющая входного сигнала. Скоро (разд. 1.18) мы также перейдем к этому немаловажную вопросу. А пока рассмотрим несколько интересных схем, для анализа которых достаточно временных зависимостей.

Упрощение с помощью эквивалентного преобразования Тевенина. Можно было бы приступить к анализу более сложных схем, пользуясь, как и раньше, методом решения дифференциальных уравнений. Однако чаще всего не стоит прибегать к решению дифференциальных уравнений.

Большинство схем можно свести к RC-схеме, показанной на рис. 1.34.

Рис. 1.34.

Пользуясь эквивалентным преобразованием для делителя напряжения, образованного резисторами R₁ и R₂, можно определить U(t) для скачка входного напряжения U_вх.

_{Упражнение 1.14. Для схемы, показанной на рис. 1.34, R1 = R2 = 10 кОм и С = 0,1 мкФ. Определите U(t) и изобразите полученную зависимость в виде графика.}

Пример: схема задержки. Мы уже упоминали логические уровни — напряжения, определяющие работу цифровых схем. На рис. 1.35 показано, как с помощью конденсаторов можно получить задержанный импульс.

Рис 1.35. Использование RC-цепи для формирования задержанного цифрового сигнала.

В виде треугольников изображены КМОП-буферные усилители. Они дают высокий уровень на выходе (более половины величины напряжения питания постоянного тока) и наоборот. Первый буферный усилитель воспроизводит входной сигнал и обеспечивает небольшое выходное сопротивление, предотвращая тем самым воздействие на источник сигнала RС-цепи (вопрос о нагрузке схемы мы рассмотрели в разд. 1.05). Согласно характеристике RС-цепи, выходной сигнал для нее задерживается относительно входного, поэтому выходной буферный усилитель переключается на 10 мкс позже скачка напряжения на входе (напряжение на выходе RС-цепи достигает 50 % своего максимального значения через 0,7RC.

На практике приходится принимать во внимание отклонение входного порога буфера от величины, равной половине напряжения питания, так как это отклонение изменяет задержку и ширину выходного импульса. Иногда подобную схему используют для того, чтобы задержать импульс на время, в течение которого может произойти какое-либо событие. При проектировании схем лучше не прибегать к подобным трюкам, но иногда они бывают полезны.

1.14. Дифференцирующие цепи

Рассмотрим схему, изображенную на рис. 1.36.

Рис. 1.36.

Напряжение на конденсаторе С равно U_вх — U, поэтому

I = Cd(U_вх — U)/dt = U/R.

Если резистор и конденсатор выбрать так, чтобы сопротивление R и емкость С были достаточно малыми и выполнялось условие dU/dt << dU_вх/dt, то

C(dU_вх/dt) = U/R или U(t) = RC[dU_вх(t)/dt].

Таким образом, мы получили, что выходное напряжение пропорционально скорости изменения входного сигнала.

Для того чтобы выполнялось условие dU/dt << dU_вх/dt, произведение RC должно быть небольшим, но при этом сопротивление R не должно быть слишком малым, чтобы не «нагружать» вход (при скачке напряжения на входе изменение напряжения на конденсаторе равно нулю и R представляет собой нагрузку со стороны входа схемы). Более точный критерий выбора для R и С мы получим, когда изучим частотные характеристики. Если на вход схемы подать прямоугольный сигнал, то сигнал на выходе будет иметь вид, представленный на рис. 1.37.

Рис. 1.37. Выходной сигнал (верхний), снимаемый с дифференциатора, на вход которого подается прямоугольный сигнал.

Дифференцирующие цепи удобно использовать для выделения переднего и заднего фронтов импульсных сигналов, и в цифровых схемах можно иногда встретить цепи, подобные той, которая показана на рис. 1.38.

Рис. 1.38. Выделение переднего фронта импульса.

Дифференцирующая RC-цепь генерирует импульсы в виде коротких пиков в моменты переключения входного сигнала, а выходной буферный усилитель преобразует эти импульсы в короткие прямоугольные импульсы. В реальных схемах отрицательный пик бывает небольшим благодаря встроенному в буфер диоду (речь об этом элементе пойдет в разд. 1.25).

Паразитная емкостная связь. Иногда схема неожиданно начинает проявлять дифференцирующие свойства, причем в ситуациях, где они совершенно нежелательны. При этом можно наблюдать сигналы, подобные показанным на рис. 1.39.

Рис. 1.39.

Первый сигнал (а точнее, импульсная помеха) может возникнуть при наличии емкостной связи между рассматриваемой линией и схемой, в которой присутствует прямоугольный сигнал; причиной появления подобной помехи может служить отсутствие оконечного резистора в линии. Если же резистор есть, то следует либо уменьшить сопротивление источника сигналов для линии, либо найти способ ослабления емкостной связи с источником сигналов прямоугольной формы. Сигнал второго типа можно наблюдать в цепи, по которой должен проходить сигнал прямоугольной формы, при наличии дефекта в контакте с этой цепью, например, в щупе осциллографа. Небольшая емкость, возникающая при плохом контакте, и входное сопротивление осциллографа образуют дифференцирующую цепь. Если вы обнаружили, что ваша схема «что-то» дифференцирует, то сказанное может помочь вам найти причину неисправности и устранить ее.

1.15. Интегрирующие цепи

Рассмотрим схему, изображенную на рис. 1.40.

Рис. 1.40.

Напряжение на резисторе R равно U_вх — U, следовательно, I = C(dU/dt) = (U_вх — U)/R. Если обеспечить выполнение условия U << U_вх за счет большого значения произведения RC, то получим C(dU/dt) ~= U_вх/R или

Мы получили, что схема интегрирует входной сигнал во времени! Рассмотрим, каким образом эта схема обеспечивает аппроксимацию интегрирования в случае входного сигнала прямоугольной формы: U(t) представляет собой знакомый уже нам график экспоненциальной зависимости, определяющей заряд конденсатора (рис.  1.41).

Рис. 1.41.

Первый участок экспоненты (интеграл от почти постоянной величины) — прямая с постоянным углом наклона; при увеличении постоянной времени RC используется все меньший участок экспоненты, тем самым обеспечивается лучшая аппроксимация идеального пилообразного сигнала.

Отметим, что условие U << U_вх равносильно тому, что ток пропорционален напряжению U_вх. Если бы в качестве входного сигнала выступал ток I(t), а не напряжение, то мы получили бы идеальный интегратор. Источником тока может служить резистор с большим сопротивлением и с большим падением напряжения на нем, и на практике часто пользуются этим приближением.

В дальнейшем, когда мы познакомим вас с операционными усилителями и обратной связью, вы узнаете, как построить интегратор, не прибегая к условию U_вых << U_вх. Такой интегратор работает в широком диапазоне частот и напряжений с пренебрежимо малой ошибкой.

Интегрирующие цепи находят широкое применение в аналоговой технике. Их используют в управляющих системах, схемах с обратной связью, при аналого-цифровом преобразовании и генерации колебаний.

Генераторы пилообразного сигнала. Теперь вы без труда разберетесь в том, как работает генератор пилообразного сигнала. Эта схема хорошо зарекомендовала себя и нашла очень широкое применение: ее используют во время-задающих схемах, в генераторах синусоидальных и других типов колебаний, в схемах развертки осциллографов, в аналого-цифровых преобразователях. Схема использует постоянный ток для заряда конденсатора (рис. 1.42).

Рис. 1.42. Источник постоянного тока, заряжающий конденсатор, генерирует напряжение в виде линейно-меняющегося сигнала.

Из уравнения для тока, протекающего через конденсатор, I = C(dU/dt) получим U(t) = (I/C)t. Выходной сигнал изображен на рис. 1.43.

Рис. 1.43.

Линейное нарастание сигнала прекращается тогда, когда «иссякает» напряжение источника тока, т. е. достигается его предельное значение. Кривая для простой RC-цепи с резистором, подключенным к источнику напряжения, ведет себя аналогично случаю достижения предела источником тока. На рис. 1.43 эта вторая кривая показана для случая, когда R выбрано так, чтобы ток при нулевом выходном напряжении был равен току источника тока; при этом вторая кривая стремится к тому же пределу, что и ломаная. (В реальных источниках тока выходное напряжение ограничено напряжением используемых в них источников питания, так что такое поведение вполне правдоподобно.) В следующей главе, посвященной транзисторам, мы построим простые схемы источников тока, а в главах, где рассматриваются операционные усилители и полевые транзисторы, — их усовершенствованные типы.

Вот как много интересных вопросов ожидает нас впереди.

_{Упражнение 1.15. Ток 1 мА заряжает конденсатор емкостью 1 мкФ. Через какое время напряжение достигнет 10 В?}

цепь переменного тока содержащая емкость индуктивность и сопротивление



цепь переменного тока содержащая емкость индуктивность и сопротивление

38)

ЦЕПЬ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩАЯ ЕМКОСТЬ

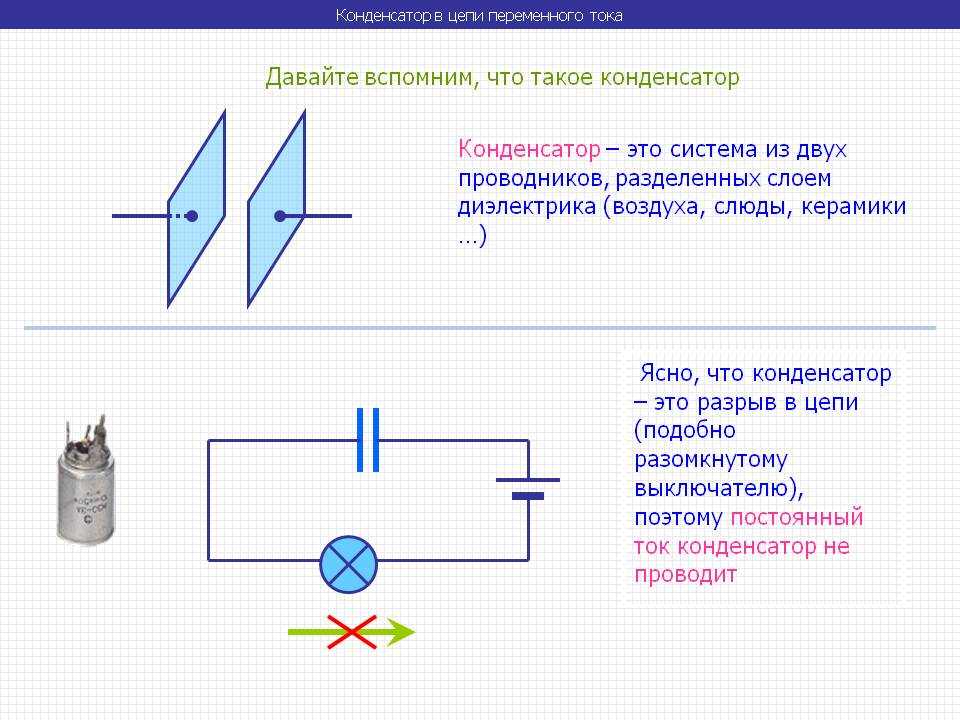
Если в цепь постоянного, тока включить конденсатор (идеаль­ный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конден­сатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.

По мере накопления зарядов на обкладках конденсатора напря­жение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения  Um, напряжение конденсатора также станет равным Um, заряд конден­сатора прекращается и ток в цепи становится равным нулю. Ток в цепи конденсатора можно определить по формуле

где ∆q — количество электричества, протекающее по цепи за время ∆t.

 Из электростатики известно:

где   С — емкость конденсатора;

u — напряжение сети;

uc — напряжение конденсатора. Окончательно для тока имеем

Из последнего выражения видно, что, когда  ∆u/∆t   максимально (положения a, в, d),  i также максимально.

 

Когда  ∆u/∆t   = 0 (положения   б, г на рис. 143), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшать­ся, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.

В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.

Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению Uc, приложенному к конденсатору, угловой частоте w и величине емкости конденсатора  C:

Обозначим

Величина Хс называется емкостным сопротивле­нием, или реактивным сопротивлением ем­кости, и измеряется в омах. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид

Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или   реактивной   слагающей   напряжения)   и   обозначается   Uc:

Емкостное сопротивление Хс, так же как индуктивное сопро­тивление xL, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет умень­шаться.

Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:

при частоте 400 гц:

 

На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

Энергию, запасаемую конденсатором к моменту, когда напряже­ние на нем равно максимальному значению, можно определить по известной формуле CU2м/2.

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии пов­торяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.

Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.

Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда wt = 45°, 135° и т. д.) достигает максимального значения, равного

 

Этой величиной принято характеризовать количественно про­цесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.

Учитывая,, что в рассматриваемой цепи U = IХc, получим сле­дующее выражение для реактивной мощности:

Электрические конденсаторы в цепях переменного тока

Написано Джоном Мортоном, CUSP, , 13 января 2014 г. , . Опубликовано в темах задней двери.

В выпуске Tailgate этого месяца мы обсудим функции конденсатора в цепи переменного тока (AC), включая заряд и разряд, применение и соединения в силовых цепях, а также безопасность конденсатора.

Электрический конденсатор представляет собой электрическое устройство, которое накапливает электричество или электрическую энергию и улучшает коэффициент мощности цепи переменного тока. Он состоит из трех основных частей. Две обычно представляют собой металлические пластины, разделенные и изолированные третьей частью, известной как диэлектрик. Заряд конденсатора зависит от размера и расстояния между проводящими пластинами, а также от типа изолирующей или диэлектрической среды между пластинами.

Все конденсаторы, независимо от типа, обозначаются по их зарядной емкости. Для цепей приборов, таких как двигатели и разрядное освещение высокой интенсивности, конденсаторы обозначаются фарадами, единицей электрической емкости, названной в честь британского ученого Майкла Фарадея.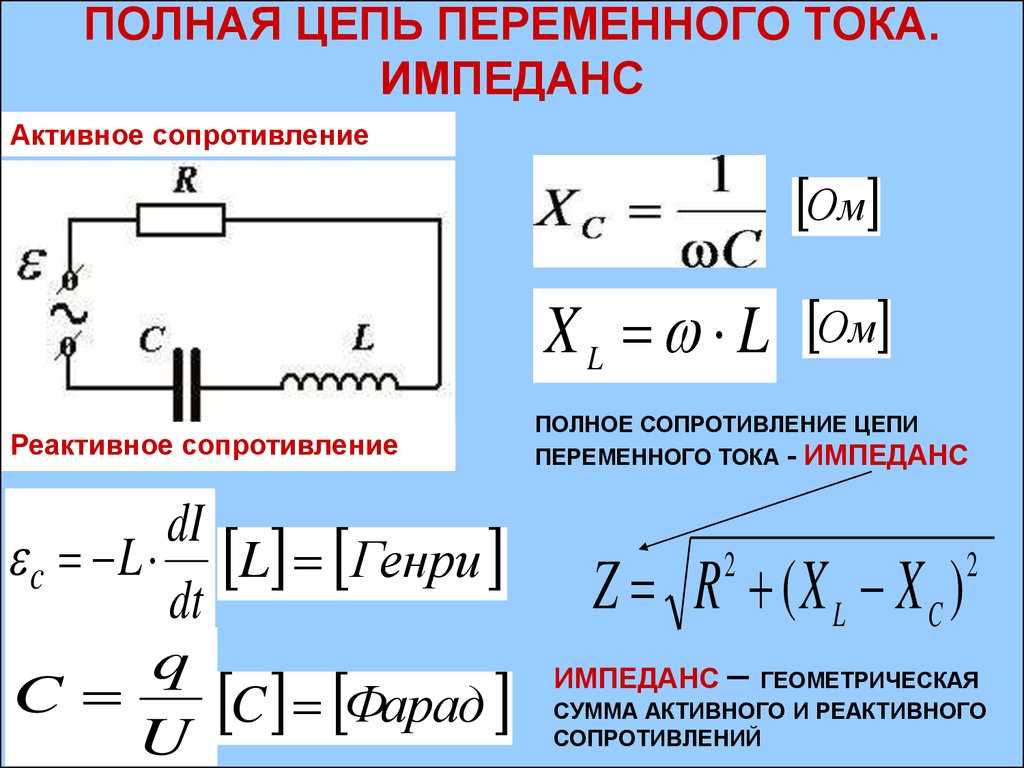 В распределении электроэнергии конденсаторы обозначаются в реактивных киловольт-амперах или кВАр для простоты применения. Счетчики спроса измеряют потребность в коэффициенте мощности в кВАр. Если двигательная нагрузка потребителя помещает на линию индуктивную нагрузку 700 квар, это можно исправить, подключив к линии емкостную мощность 700 квар. Это не так просто, но вы поняли идею.

Зарядка и разрядка конденсатора в цепи переменного тока
Конденсатор немного похож на батарею. Хотя они работают совершенно по-разному, конденсаторы и батареи хранят электрическую энергию. Вы знаете, что аккумулятор имеет две клеммы. Внутри батареи химические реакции производят электроны на одном выводе и поглощают электроны на другом. Конденсатор — гораздо более простое устройство, и он не может производить новые электроны — он только хранит их.

Например, когда вы видите молнию в небе, вы видите огромный конденсатор. Одна пластина — это облако, другая пластина — это земля, а молния — это заряд, высвобождающийся между этими двумя пластинами. Очевидно, что в таком большом конденсаторе вы можете удерживать огромное количество заряда.

Применение в силовых цепях
Конденсаторы следует устанавливать осторожно и правильно. Как указывалось ранее, целью конденсатора является улучшение коэффициента мощности схемы. Конденсатор только корректирует коэффициент мощности от конденсатора обратно в систему. Конденсаторы не оказывают влияния на коэффициент мощности между конденсатором и реактивной нагрузкой, вызывающей коэффициент мощности. Неправильно примененные конденсаторы могут обеспечить больший реактивный ток, чем требуется нагрузке, что приводит к опережающему коэффициенту мощности и увеличению потерь вместо их уменьшения. Вот почему конденсаторы расположены после тщательного изучения системы квалифицированными инженерами.

Соединения в силовых цепях
Установка одного конденсатора или группы конденсаторов является простой процедурой после определения правильного размера и места установки. Конденсатор во многих отношениях проще в установке, чем трансформатор, потому что в нем нет вторичных вводов, а конденсатор представляет собой герметичный блок. В одних блоках две втулки, в других одна.

Распределительные конденсаторы с двумя изолированными вводами обычно подключаются между фазами, но могут быть подключены фаза к земле. Конденсаторы с одним изолированным вводом обычно подключают фазой к изолированному вводу, а корпусом к земле. В установках подстанции конденсаторы распределительного напряжения соединены параллельно, разделяя фазные напряжения передачи. Они установлены на изолированном каркасе, который является частью межсоединения, работающего на фазном напряжении передачи. Любой, кто работает с любым конденсатором, должен хорошо знать, как он подключен и при каком напряжении работает.

Вам также следует знать о постоянных и переключаемых конденсаторах. Эти термины просто относятся к способу подачи питания на конденсатор. Если он зафиксирован, ввод, подключенный к источнику, идет непосредственно к предохранителю.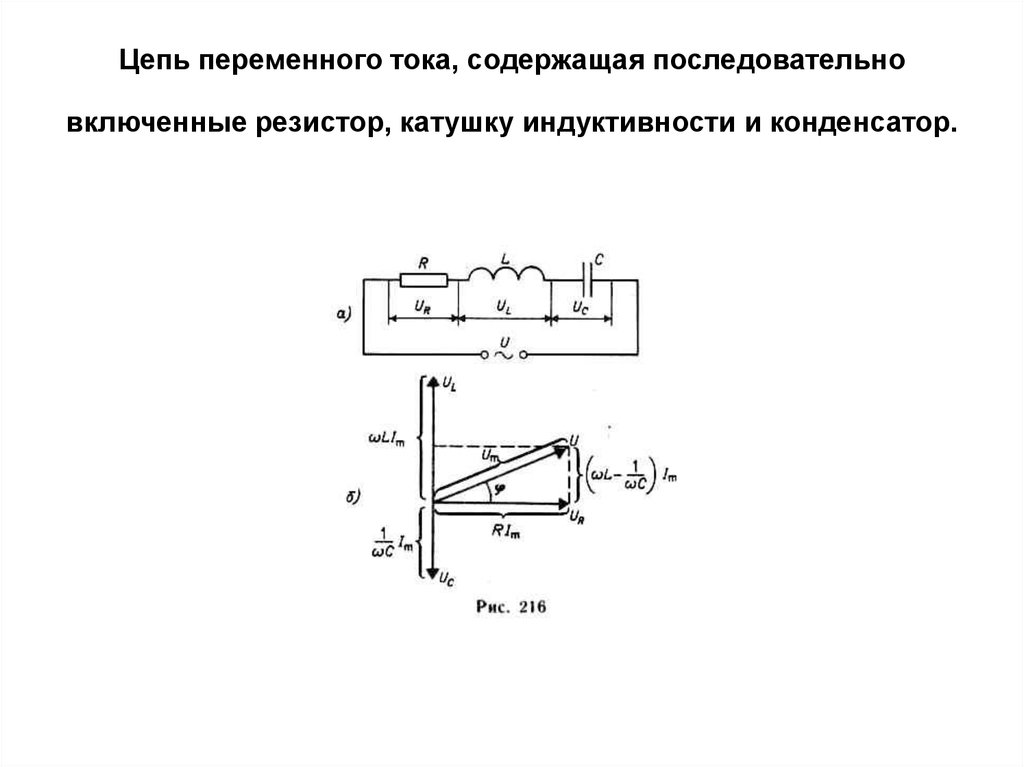 Этот предохранитель является единственным средством включения или выключения конденсатора. В случае коммутируемого конденсатора ввод, подключенный к источнику, идет к коммутационному устройству, включенному последовательно между предохранителем и конденсатором. Назначение этого переключающего устройства состоит в том, чтобы позволить конденсатору работать в то время, когда он наиболее необходим. Существует много типов элементов управления, которые определяют, должен ли конденсатор быть включен или выключен в зависимости от требований системы. Ниже приведены примеры элементов управления и то, для чего они чаще всего используются:
• Контроль времени используется в районах, где известно, что нагрузка возникает через определенные промежутки времени либо из-за промышленного использования, либо из-за бытовых требований.
• Текущий контроль используется в областях, где нагрузка клиента непостоянна и не всегда присутствует в одно и то же время суток.
• Температурный контроль используется в областях, где сезонные изменения создают большую индуктивную нагрузку на систему (например, кондиционирование воздуха). В основном доступны два основных регулятора температуры: включение при 85 градусах и выключение при 65 градусах или включение при 9 градусах.0 градусов и выключается при 70 градусах.
• Управление напряжением используется в областях, где нагрузка вызывает легко контролируемое падение напряжения в системе. Регуляторы напряжения также часто используются в сочетании с регуляторами времени, тока и температуры.
• Ручное управление используется для облегчения отключения переключаемой группы, которая часто используется для сезонной нагрузки.

Безопасность конденсаторов
Хотя конденсаторы являются простыми устройствами, они чрезвычайно опасны после отключения от эксплуатации, поскольку могут сохранять заряд. Они должны быть построены с стабилизирующими резисторами, которые снижают их напряжение до менее чем 50 вольт через пять минут. Однако никогда ничего не принимайте как должное. Крайне важно подождать пять минут после отсоединения, а затем закоротить втулки проволочной перемычкой с помощью ружейной палки. Перед началом работы с любым конденсатором, установленным на столбе, всегда выполняйте следующие процедуры, поскольку конденсатор может удерживать заряд без каких-либо признаков того, что он это делает.

При выводе конденсаторов из эксплуатации невозможно выделить следующие шаги:
• Отключить от источника.
• Подождите пять минут, пока разрядится заряд.
• Замкните накоротко втулки или, в случае конденсаторов с одной втулкой, закоротите втулку и корпус.
• Сохраняйте короткозамыкающее соединение до тех пор, пока конденсатор не будет подключен для обслуживания.

Об авторе: Джон Мортон, CUSP, начал свою карьеру в электротехнической промышленности в 1970 лет в качестве наземного работника компании Houston Lighting and Power, ныне известной как CenterPoint Energy. В 1997 году он устроился на работу в службу распространения знаний Техасского университета A&M в качестве инструктора по электротехнике и связи, а в 2004 году он занял свою нынешнюю должность директора по безопасности и обучению в Willbros T&D Services в Техасе.

 

Цепи конденсаторов переменного тока и емкостное реактивное сопротивление

Краткое описание

Введение

[adsense1]

Когда на конденсатор подается напряжение питания постоянного тока, он медленно заряжается и, наконец, достигает полностью заряженного состояния. В этот момент зарядное напряжение конденсатора равно напряжению питания. Здесь конденсатор действует как источник энергии, пока подается напряжение. Конденсаторы не пропускают через себя ток (i) после полной зарядки. Ток, протекающий по цепи, зависит от количества заряда на пластинах конденсатора, а также ток прямо пропорционален скорости изменения напряжения, приложенного к конденсатору. схема. т. е. i = dQ/dt = C dV(t)/dt.

Если к цепи конденсатора приложено напряжение питания переменного тока, то конденсатор непрерывно заряжается и разряжается в зависимости от частоты напряжения питания. Емкость конденсатора в цепях переменного тока зависит от частоты приложенного к нему питающего напряжения. В цепях переменного тока конденсаторы пропускают ток, когда напряжение питания непрерывно изменяется во времени.

Цепь конденсатора переменного тока

В приведенной выше схеме мы заметили, что конденсатор напрямую подключен к напряжению питания переменного тока. Здесь конденсатор постоянно заряжается и разряжается в зависимости от изменения напряжения питания, потому что значение переменного напряжения питания постоянно увеличивается и уменьшается. Все мы знаем, что ток, протекающий по цепи, прямо пропорционален скорости изменения приложенного напряжения.

Здесь зарядный ток имеет свое высокое значение, если напряжение питания переходит его значение из положительного полупериода в отрицательный полупериод и наоборот. то есть в точках 0 ⁰ и 180 ⁰ в синусоидальном сигнале. Ток через конденсатор имеет минимальное значение, когда напряжение питания в виде синусоиды пересекает свое максимальное или минимальное пиковое значение (Vm).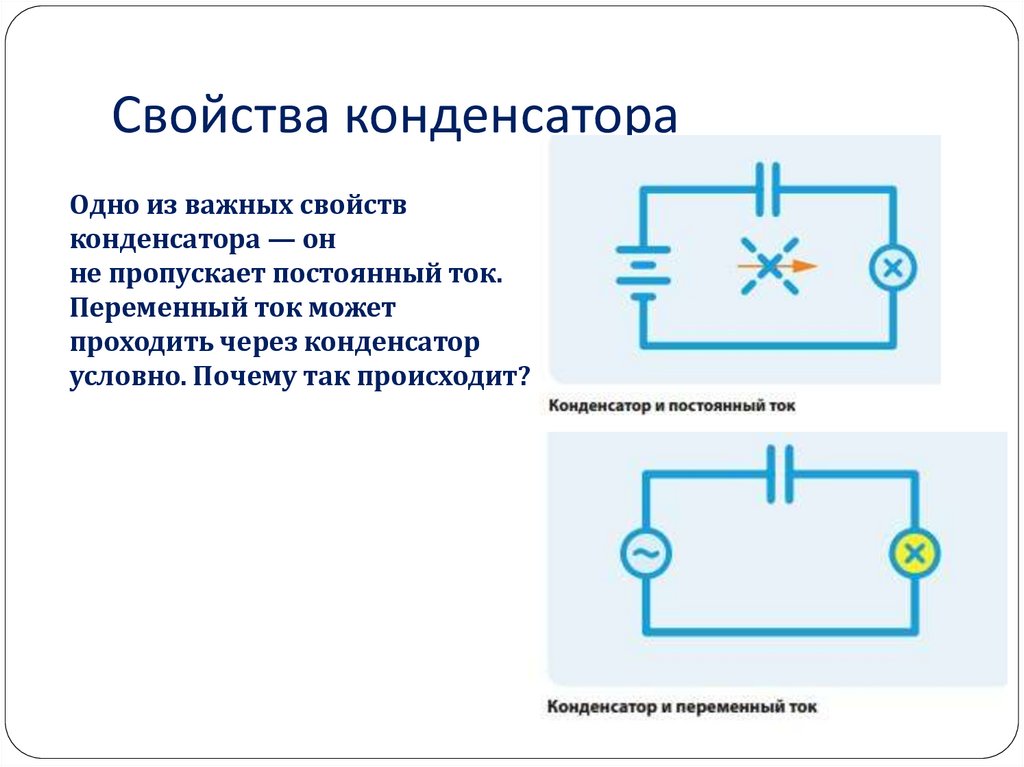 Следовательно, мы можем сказать, что зарядный ток, протекающий через цепь, максимален или минимален в зависимости от уровней напряжения питания в виде синусоиды.

[adsense2]

Векторная диаграмма конденсатора переменного тока

 

Векторная диаграмма конденсатора переменного тока показана на рисунке выше, здесь напряжение и ток представлены в виде синусоидальных волн. На приведенном выше рисунке мы заметили, что при 0 ⁰ зарядный ток достигает своего максимального значения, поскольку напряжение медленно увеличивается в положительном направлении. В точке 90 ⁰ ток через конденсатор не течет, потому что в этой точке напряжение питания достигает своего максимального пикового значения.

В точке 180 ⁰ напряжение медленно снижается до нуля, а ток достигает максимального значения в отрицательном направлении. Снова зарядка достигает своего максимального значения на 360 ⁰ , потому что в этот момент напряжение питания имеет минимальное значение.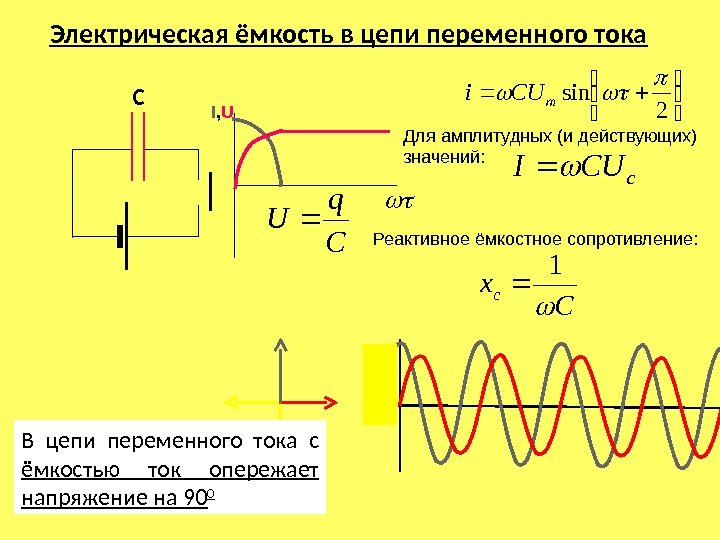

Из осциллограмм на рисунке выше видно, что ток опережает напряжение на 90 ⁰ . Отсюда можно сказать, что в идеальной конденсаторной цепи переменное напряжение отстает от тока на 90 ⁰ .

Емкостное реактивное сопротивление

Мы знаем, что ток, протекающий через конденсатор, прямо пропорционален скорости изменения приложенного напряжения, но конденсаторы также обладают определенным сопротивлением потоку тока, как и резисторы. Это сопротивление конденсаторов в цепях переменного тока называется емкостным реактивным сопротивлением или широко известно как реактивное сопротивление. Емкостное реактивное сопротивление — это свойство конденсатора, противодействующее протеканию тока в цепях переменного тока. Оно обозначается символом Xc и измеряется в Омах так же, как сопротивление.

Нам нужна дополнительная энергия по сравнению с емкостным реактивным сопротивлением, чтобы зарядить конденсатор в цепи. Это значение обратно пропорционально значению емкости и частоте питающего напряжения.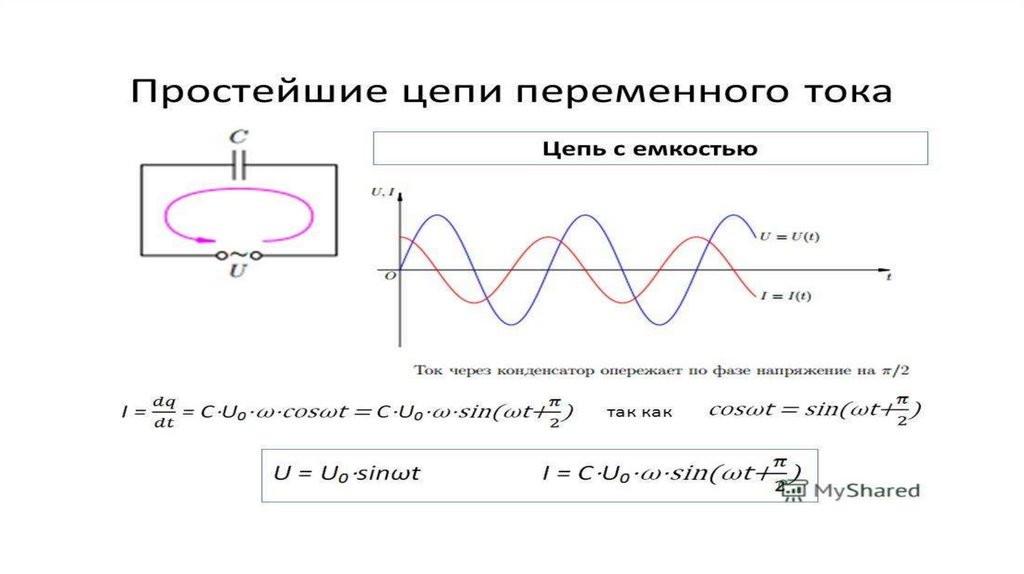

Xc∝ 1/c и Xc∝ 1/f.

Уравнение для емкостного сопротивления и параметры, влияющие на него, обсуждаются ниже.

Емкостное реактивное сопротивление,

XC = 1/2πfC = 1/ωC ​​

Здесь,

XC = реактивное сопротивление конденсатора

f = частота в Гц

C = емкость конденсатора в фарадах

ω (омега) = 2πf

Из приведенного выше уравнения мы поняли, что емкостное реактивное сопротивление высокое там, где значения частоты и емкости низкие, и на этом этапе конденсатор действует как идеальный резистор. Если частота питающего напряжения высокая, то значение реактивного сопротивления конденсатора низкое, а также на этом этапе конденсатор действует как хороший проводник. Из приведенного выше уравнения ясно, что реактивное сопротивление равно нулю, если частота равна бесконечности, а значение реактивного сопротивления равно бесконечности, когда частота равна нулю.

Емкостное сопротивление в зависимости от частоты

На приведенном выше рисунке показано соотношение между емкостным сопротивлением, током и частотой питающего напряжения.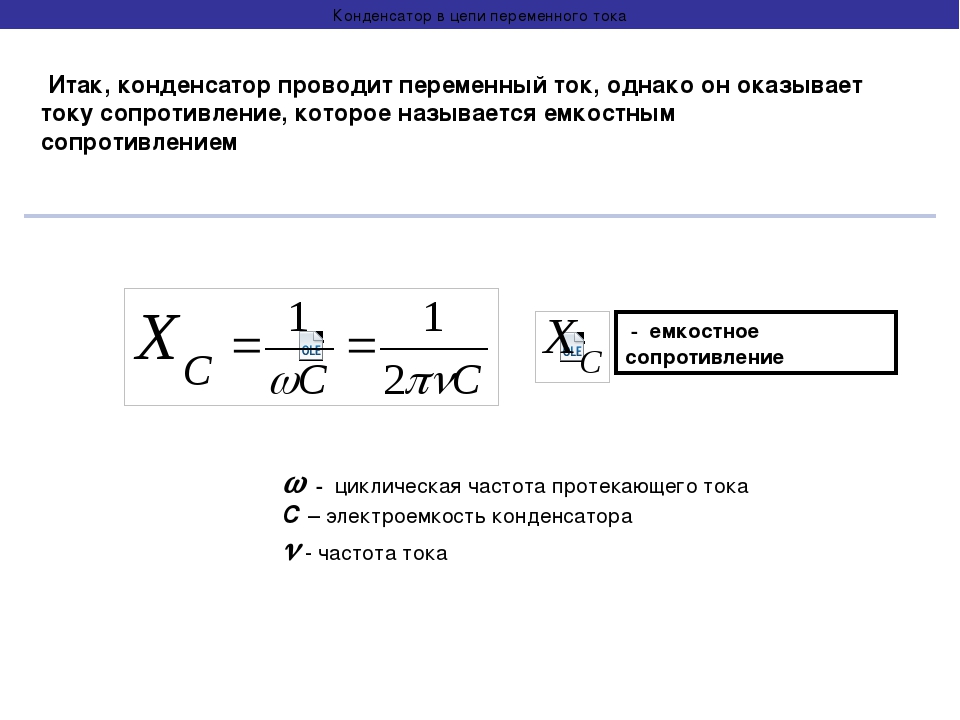 Здесь мы заметили, что если частота низкая, реактивное сопротивление высокое. Зарядный ток увеличивается с увеличением частоты, потому что скорость изменения напряжения увеличивается со временем. Реактивное сопротивление имеет бесконечное значение, когда частота равна нулю, и наоборот.

Пример емкости переменного тока №1

Найдите среднеквадратичное значение тока, протекающего через цепь с конденсатором 3 мкФ, подключенным к источнику питания 660 В и 40 Гц.

емкоспорт,

XC = 1/2πfc

Здесь,

F = 40 Гц

C = 3UF

VRMS = 660V

СЕЙЧАС,

xC = 1/(2 × 3,14 × 40HZ × 3 × 3 × 3 × 3 × 3 × 3 × 3 40HZ. 10 ^-6 ) = 1326 Ом

Irms = Vrms/XC = 660 В/1326 Ом = 497 мА

Пример емкости по переменному току №2

Найдите среднеквадратичное значение тока, протекающего через цепь с конденсатором 5 мкФ, подключенным к источнику питания 8080 В.

емкоспорт,

XC = 1/2πFC

Здесь,

F = 50 Гц

C = 5UF

VRMS = 880V

СЕЙЧАС,

XC = 1/(2 × 3,14 × 50HZ × 5 × 5 × 5 × 5 ° × 50005

xc = 1/(2 × 3,14 × 50HZ × 50005

xc = 1/(2 × 3,14.