Коэффициент заполнения графика нагрузки: 8.4.4. Коэффициент формы графика нагрузки

Содержание

8.4.4. Коэффициент формы графика нагрузки

Коэффициент формы
графика нагрузки — это отношение
среднеквадратичной (эффективной)
р_э,
Р_э
нагрузки к средней р_с,
Р_с
за данный период времени:

(8.21)

(8.22)

Коэффициент формы
графика нагрузки группы из n
приемников определяется так же:

(8.23)

Введем величину
которую назовем эффективным числом
приемников.

(8.24)

Тогда коэффициент
формы

(8.25)

Следовательно,
вариация суммарного графика нагрузки

(8.26)

Если все приемники
имеют одинаковую номинальную мощность
р_ном,
то

n_э
= [(пр_ном)²]/[пр_ном]²
(8. 27)

В общем случае
п_э≤п.

Если все приемники
группы имеют однородный график работы,
т. е. k_ф_i=
k_ф,
тогда

K_ф
= k_ф (8.28)

При п_э
→ ∞ коэффициент формы K_ф
→ 1, это означает, что при неограниченном
возрастании числа приемников групповой
график для стационарного режима
становится постоянным с минимальной
вариацией, т. е. γ_Σ→ 0. Для
реальных графиков нагрузки на интервалах
стационарности, например в период
максимума нагрузок, K_ф
= 1,02… 1,25, однако для объектов с достаточно
ритмичным процессом K_ф
= 1,05… 1,15. Данные выводы справедливы для
графиков нагрузок групп, объединяющих
значительное число приемников, например
шины трансформаторных подстанций.

8.4.5. Коэффициент заполнения графика

Коэффициентом
заполнения графика нагрузок активной
мощности
называется отношение средней активной
мощности за исследуемый период времени
к максимальной за тот же период:

Следует отметить,
что максимальная нагрузка определяется
исходя из периода осреднения графика
нагрузки, равного 0,5 ч, т. е. за основу
берется так называемый получасовой
максимум нагрузки. Для практических
расчетов принимается, что вероятность
превышения получасового максимума
не больше 0,005, т.е. при этом P_max=
Р_c+ 2,5σ_p.
Тогда

(8.29)

Следовательно,
чем меньше вариация нагрузки γ_p,
тем больше коэффициент заполнения
графика, и при γ_p
→ 0 коэффициент заполнения графика
→
1. При K_ф
= 1,1 (γ_p
≈ 0,5)≈
0,45.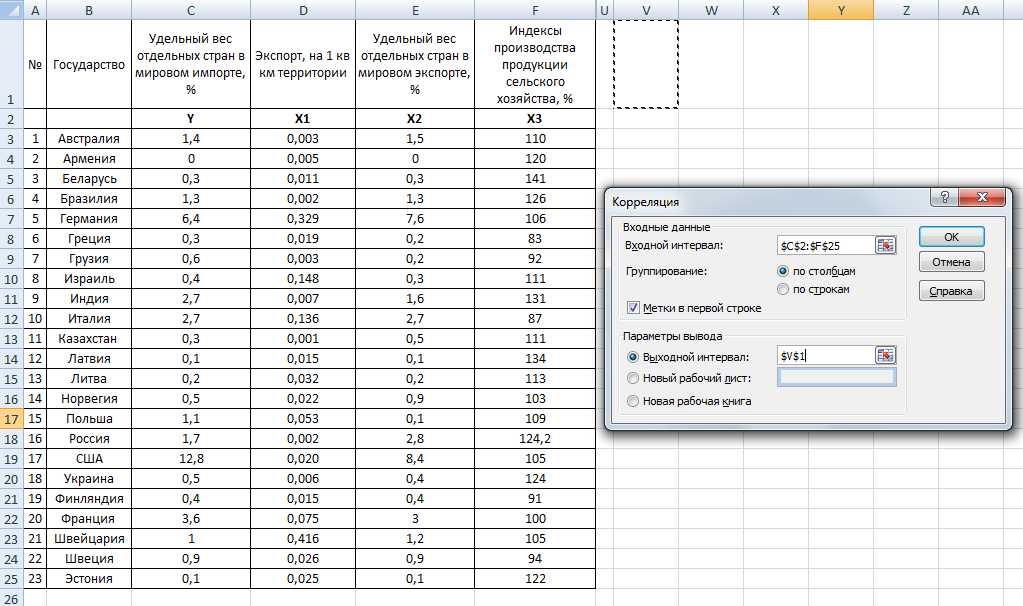

Для характеристики
заполнения графика нагрузки используют
также понятие числа часов использования
максимальной нагрузки

(8.30)

где Э_г
— годовой расход активной электроэнергии
объекта.

8.4.6. Коэффициент энергоиспользования

Неравномерность
нагрузки по сменам, работу в праздничные
дни, а также сезонные колебания нагрузки
учитывает годовой коэффициент
энергоиспользования К_эг,
который устанавливает связь между
средними активными нагрузками за смену
Р_с
и среднегодовыми нагрузками Р_с_г:

(8.31)

где Р_с

г —
среднегодовая нагрузка, равная
годовое
число часов работы.

(8.32)

где Т_см
— продолжительность смены; Т_пр
— годовое число часов, на которое
сокращена продолжительность работы в
предвыходные (предпраздничные) дни; m
— число нерабочих дней в году; n
— число смен; К_р— коэффициент,
учитывающий время ремонта и другие
простои, принимаемый равным 0,96
. ..0,98.

Годовую
продолжительность работы предприятия,
за исключением цехов с непрерывным
производством, в зависимости от числа
и продолжительности смен можно принимать
по данным табл. 8.1.

Таблица 8.1

Годовое число
часов работы предприятия

Продолжительность
смены, ч

Годовое число
часов работы при числе смен, ч

одна

две

три

2250

2000

4500

3950

6400

5870

Для предприятий
и цехов с непрерывным производством
годовое число часов работы соответственно
увеличивается.

Коэффициент
энергоиспользования К_э_г
изменяется в пределах 0,55…0,95.

1. Коэффициент заполнения суточного графика

β_сут
= Р_ср/
Р_max
= Р_ср
24/
Р_max∙24 = Э_сут
/ Э_потен_.

2. Коэффициент минимальной нагрузки:

α
= Р_min/ Р_max

Эти
показатели отражают режим электропотребления,
климат, структуру потребителя и дают
возможность сопоставлять и анализировать
графики разных масштабов.

Последнее
время характерно повышение удельного
веса жилищно-коммунальных
и сельскохозяйственных нагрузок,
сокращение ночных смен. Это приводит к
разуплотнению графиков нагрузки.
Повышение же удельного веса непрерывных
производств, улучшение загрузки
оборудования – к уплотнению графиков
нагрузки.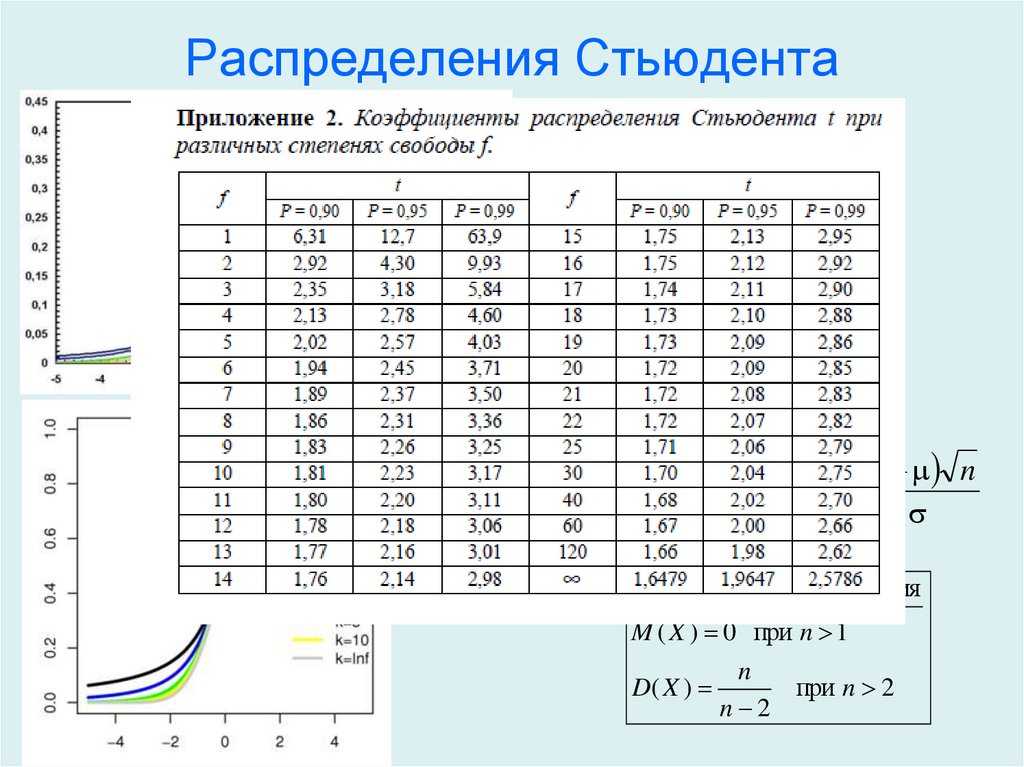

3.
Недельный график

Отражает
колебания нагрузки по дням недели,
главным образом за счет выходных и
праздничных дней. Помимо колебаний
нагрузки внутри недели имеет место
колебания между неделями, вызываемые
изменениями продолжительности светлых
часов суток, приростом нагрузки и т.д.

График недельного электропотребления.

Р_срсут
– среднесуточная нагрузка, МВт; Р_ср

нед–
средненедельная нагрузка, МВт.

Коэффициент
заполнения недельного графика

β_нед
= Р_{ср нед}/
Р_max
= Р_ср
7/
Р_max∙7 = Э_нед
/ Э_потен_.

4. Месячный график

Отражает
колебания средненедельной
нагрузки по неделям месяца. Максимум
месячного графика нагрузки приходится
на первую неделю месяца (для периода
весна-лето)
или на последнюю неделю месяца (для
периода осень-зима).
Минимум месячной нагрузки приходится
на конец месяца (весна-лето) и начало
месяца (осень-зима). Осенне-зимний
максимум нагрузки растет к концу месяца,
что связано с уменьшением продолжительности
светлых часов и внутригодового роста
нагрузки, а в весенне-летний период
наблюдается ее снижение к концу месяца.

5. Годовой график

Отражает
изменения нагрузки в пределах
года. Одной
из важных характеристик годового графика
нагрузки является показатель годового
числа часов
использования максимума нагрузки
энергосистемы.

Он
может быть определен как произведение
коэффициентов заполнения
суточного, недельного, месячного,
годового графика нагрузки и числа часов
в году.

h_c
= β_сут
β_нед
β_мес
β_год
8760,

Этот
показатель характеризует расчетное
число часов, при котором годовая
потребность в электроэнергии покрывается
при постоянной нагрузке.

Коэффициенты
заполнения годового графика
β_год
определяется по формуле:

Максимальная
нагрузка каждого периода рассматриваемого
года увеличивается по сравнению с таким
же периодом предшествующего года, их
отношение характеризуется коэффициентом
роста:

где
Р_max₁,
P_max₂
– максимум нагрузки в январе и декабре
месяцах рассматриваемого года.

Рис.
Годовые графики нагрузки

Провал
годового графика максимальных месячных
нагрузок (в основном в весенне-летний
период) используется для проведения
капитальных ремонтов оборудования.

Влияние неравномерности графика нагрузки на экономику энергосистемы

Для
энергосистемы, с точки зрения экономики,
наиболее выгодным было бы равномерное
электропотребление. Но достижение
такого положения практически невозможно.

Экономические
последствия неравномерности графика
нагрузки:

1.Требуется
большая
величина установленной мощности
электростанций, что увеличивает
капиталовложения, усложняет структуру
мощностей.

2.Увеличивается
удельный расход топлива на выработанный
кВт час, т.к. требуется ввод специальной
пиковой
ЭС, производящих электроэнергию при
очень высоких расходах топлива, или
нерационально
используются ТЭС, не приспособленные
к работ в пиковой части суточного
графика.

3.
Снижается надежность
работы оборудования в связи с более
частой разгрузкой и остановом оборудования.

Коэффициент заполнения | PVEducation

Ток короткого замыкания и напряжение холостого хода являются максимальными током и напряжением солнечного элемента соответственно. Однако в обеих этих рабочих точках мощность солнечного элемента равна нулю. «Коэффициент заполнения», более известный под аббревиатурой «FF», представляет собой параметр, который в сочетании с V _oc и I _sc определяет максимальную мощность солнечного элемента.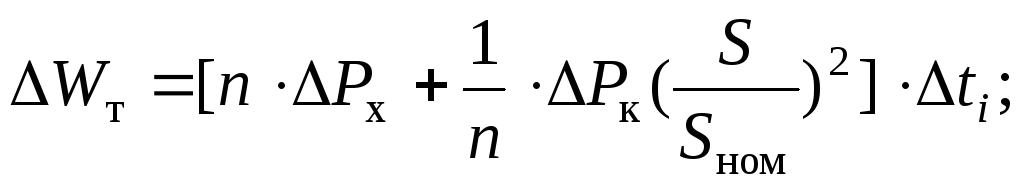 FF определяется как отношение максимальной мощности солнечного элемента к произведению V _oc и I _sc так что:

$$FF= \frac{P_{MP}}{V_{OC}\times I_{SC}}$$

FF=VMPIMPVOCISC

Графически FF является мерой «прямоугольности» солнечного элемента, а также площадью наибольшего прямоугольника, который соответствует кривой IV. FF показан ниже.

График выходного тока элемента (красная линия) и мощности (синяя линия) в зависимости от напряжения. Также показаны ток короткого замыкания ячейки (I _sc) и напряжение холостого хода (V _OC ) точек, а также точка максимальной мощности (V _mp , I _mp ). Нажмите на график, чтобы увидеть, как изменяется кривая для ячейки с низким FF.

Поскольку FF является мерой «прямоугольности» ВАХ, солнечный элемент с более высоким напряжением имеет больший возможный FF, поскольку «закругленная» часть ВАХ занимает меньшую площадь. Максимальный теоретический FF от солнечного элемента можно определить, продифференцировав мощность солнечного элемента по напряжению и найдя, где оно равно нулю. Следовательно:

$$\frac{d(IV)}{d V}=0$$

дает:

$$V_{MP} = V_{OC} — \frac{nkT}{q}ln(\frac {q V_{MP}}{nkT}+1)$$

Это неявное уравнение, но оно быстро сходится при итерации. Начиная с V _MP = 0,9 × V _OC в качестве начального условия, после одной итерации возникает ошибка < 1 % и незначительная (< 0,01 %) после трех итераций. В качестве альтернативы можно использовать функции Ламберта (см. ниже). Подстановка значения V _MP обратно в уравнение диода дает I _MP, а затем FF. Более часто используется эмпирическое выражение для FF: Приведенные выше уравнения показывают, что более высокое напряжение будет иметь более высокий возможный FF. Однако большие колебания напряжения холостого хода в данной системе материалов относительно редки. Например, при одном солнечном свете разница между максимальным напряжением холостого хода, измеренным для кремниевого лабораторного устройства и типичного коммерческого солнечного элемента, составляет около 120 мВ, что дает максимальные коэффициенты мощности 0,85 и 0,83 соответственно. Однако изменение максимального FF может быть значительным для солнечных элементов, изготовленных из разных материалов. Например, солнечный элемент GaAs может иметь FF, приближающийся к 0,89..

Приведенное выше уравнение также демонстрирует важность фактора идеальности, также известного как «n-фактор» солнечного элемента. Фактор идеальности является мерой качества перехода и типа рекомбинации в солнечном элементе. Для простых механизмов рекомбинации, обсуждаемых в разделе «Типы рекомбинации», n-фактор имеет значение 1. Однако некоторые механизмы рекомбинации, особенно если они большие, могут вводить механизмы рекомбинации, равные 2. Высокое значение n не только ухудшает FF. , но поскольку он также обычно сигнализирует о высокой рекомбинации, он дает низкие напряжения холостого хода.

Основным ограничением описанных выше уравнений является то, что они представляют собой максимально возможный FF, хотя на практике FF будет ниже из-за наличия паразитных резистивных потерь, которые обсуждаются в разделе «Влияние паразитных сопротивлений». Таким образом, FF чаще всего определяется из измерения ВАХ и определяется как максимальная мощность, деленная на произведение I _sc *V _oc , то есть:

FF=VMPIMPVOCISC

Точное определение V

_MP

Уравнение для солнечной батареи:

$$I = I_L-I_0\left[\exp\left(\frac{V}{nV_t}\right)-1\right]$$

$Мощность = V \times I$ и, кроме того, член -1 не действует при V _MP

$$P = V I_L- V I_0\exp\left(\frac{V}{nV_t}\ right)$$

V _MP это когда производная степени по V равна нулю:

$$0 = I_L- I_0\exp\left(\frac{V_{MP}}{nV_t}\right )\left(1+\frac{V_{MP}}{nV_t}\right)$$

9x \Leftrightarrow X = W (Y)$$

поэтому мы получаем:

$$\frac{V_{MP}}{nV_t} =W\left(\frac{I_L}{I_0}\right)$$

$$V_{MP} = nV_t W\left(\frac{I_L}{I_0}\right)$$

используя выражение для V _OC можно также написать:

$$V_{MP} = nV_t W\left(\exp\left(\frac{V_{OC}}{nV_t}\right)\right)$$

Поскольку выражение внутри W() всегда реальное и положительное, нам нужна только основная ветвь W-функции Ламберта, W ₀ . W-функция Ламберта — трансцендентная функция, очень похожая на функцию логарифма. Хотя он недоступен в большинстве калькуляторов, он доступен в расширенных математических пакетах, таких как Matlab или Python. При дальнейшем анализе W-функцию Ламберта можно также использовать для других элементов солнечной батареи и при наличии паразитных сопротивлений 2,9.0011

1. М. А. Грин, «Коэффициенты заполнения солнечных элементов: общий график и эмпирические выражения», Solid-State Electronics, vol. 24, стр. 788 — 789, 1981.
2. Джейн А. Точные аналитические решения параметров реальных солнечных элементов с использованием W-функции Ламберта // Материалы для солнечной энергии и солнечные элементы. 81, нет. 2, стр. 269 — 277, 2004.

Почему важно понимать коэффициент заполнения солнечной батареи? Как это влияет на эффективность фотоэлементов?

Фактор заполнения и эффективность солнечной батареи

Трудно ли понять коэффициент заполнения солнечных элементов? И обязательно ли знать коэффициент заполнения и КПД солнечной батареи?

Ответ: Нет!! Это несложно, но необходимо понять, если вы хотите узнать, как повысить эффективность солнечной батареи??

Понимание коэффициента заполнения и оптимизации эффективности солнечных батарей не является достаточно негибким, если у вас есть достаточно времени, чтобы прочитать эту часть статьи. Эта статья полна факторов заполнения и эффективности солнечной батареи.

В связи с продолжающимся ростом глобального потепления и сокращением использования ископаемого топлива цель альтернативных источников энергии становится все более и более актуальной.

На протяжении всей этой статьи я подчеркивал фактор заполнения солнечных батарей, их поведение, влияние и факторы, влияющие на эффективность солнечных батарей.

Солнечная фотогальваническая (PV) ячейка может преобразовывать световую энергию в электрическую энергию в определенных полупроводниковых материалах, таких как кремний, галлий и т. д.

Реализация более значительного потенциала только от части солнечного излучения требует изучения рабочих параметров солнечного фотоэлектрического модуля. Коэффициент заполнения (FF), напряжение холостого хода (VOC) и ток короткого замыкания (ISC) являются тремя важными жизненно важными параметрами.

Доведение до максимума всех трех параметров необходимо для эффективной работы.

Коэффициент заполнения (FF).
Напряжение холостого хода (VOC).
Ток короткого замыкания (ISC).

Глубокое понимание технических особенностей факторов необходимо для рентабельной работы.

Давайте начнем с коэффициента заполнения и эффективности солнечных элементов, их определения и формулы, а также оценим ограничивающий характер в различных обстоятельствах.

Давайте углубимся!!

Содержание

Что означает коэффициент заполнения и эффективность солнечной батареи?
- Значение коэффициента заполнения по формуле:
- Pmax = VMPP x IMPP
Коэффициент заполнения солнечных элементов:
- Эффективность солнечного элемента:
Разница между коэффициентом заполнения и коэффициентом заполнения
Факторы, влияющие на эффективность фотоэлектрического элемента:
Как повысить эффективность солнечного элемента:
Почему солнечные элементы не могут достичь 100-процентной эффективности:
Окончательная мысль о коэффициенте заполнения солнечного элемента:

Что означает коэффициент заполнения и эффективность солнечной батареи?

Значение коэффициента заполнения по формуле :

Коэффициент заполнения (FF) обычно является мерой эффективности солнечного фотоэлектрического модуля.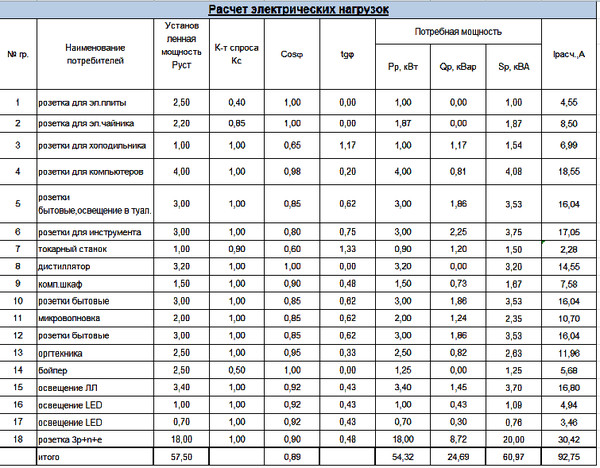

FF — это отношение максимальной мощности (P _max) к произведению V _OC и I _SC, то есть:

Это отношение фактической максимально достижимой мощности.

Здесь,

Напряжение разомкнутой цепи (V _OC ): Максимальное напряжение, которое может генерировать солнечная фотоэлектрическая панель (при стандартных условиях испытаний). Поскольку к выходной цепи не подключена нагрузка, ток не возникает.

Ток короткого замыкания (I _SC ): Максимальный ток, который может генерировать солнечная фотоэлектрическая панель (при стандартных условиях испытаний). Поскольку провода панели соединены напрямую, т. е. закорочены, напряжения не возникает.

Формула коэффициента заполнения — диаграмма коэффициента заполнения

Максимальная мощность (P _max ) возникает, когда комбинации тока и напряжения дают наиболее значительную мощность.

Не происходит ни при разомкнутой цепи (V _OC) , ни при коротком замыкании (I _SC) .

Так как при I _SC напряжение идеально равно нулю, а при V _OC ток в ячейке тоже считается идеально нулевым.

Следовательно, P _max не возникает при максимальном токе; скорее, это происходит при конкретном токе (I _MPP) , который меньше, чем I _SC .

Аналогично, P _max не возникает при максимальном напряжении; скорее, это происходит при определенном напряжении (V _MPP), которое меньше, чем V _OC.

Таким образом,

P _max = V _MPP x I _MPP

Здесь В _MPP и I _MPP — это напряжение и ток соответственно в точке максимальной мощности на кривой зависимости тока (I) от напряжения (V) (т. е., IV кривая).

Коэффициент заполнения солнечных элементов:

Коэффициент заполнения (FF) солнечного фотоэлектрического модуля обычно составляет около 80% для кремниевых элементов.
А солнечные элементы из GaAs могут дать максимальный КФ 89%.

Эффективность солнечной батареи:

Эффективность солнечной батареи определяется мощностью солнечной панели.

Отношение наибольшей мощности к входной мощности.

Здесь P _max — это максимальная мощность, которую солнечная фотоэлектрическая панель может генерировать при стандартных условиях испытаний

Коэффициент заполнения и эффективность солнечной батареи

И, P _в — солнечное излучение, т. е. лучистая энергия, испускаемая солнцем.

Как правило, существует три разновидности солнечных панелей, а именно:

Монокристаллические,
Поликристаллический и
Тонкопленочный.

Эффективность преобразования трех типов солнечных батарей зависит от их конструкционных материалов и технологий.

Солнечная батарея	Строительство	Эффективность (%))
я. Монокристаллический	Чистый кремний	20
ii. Поликристаллический	Фрагменты кремниевого кристалла, расплавленные вместе	15 – 17
III. Тонкопленочный	Теллурид кадмия (CdTe), аморфный кремний (a-Si) и селенид меди, индия, галлия (CIGS) или любая такая смесь из различных материалов	11 (приблизительно)

Монокристаллические солнечные панели: Их производственным материалом является чистый кремний. Они и самые дорогие, и самые эффективные. Монокристаллические солнечные панели могут достигать КПД более 20%.

Поликристаллические солнечные панели: Технология их изготовления немного отличается от других, несмотря на то, что материалом изготовления является кремний. Фрагменты кристалла кремния сплавлялись вместе для производства поликристаллических солнечных панелей.

Целью разработки поликристаллической солнечной панели было снижение стоимости, однако она также стала менее эффективной.

Как правило, эффективность может достигать 15–17 %.

Этот разрыв в эффективности между двумя вышеупомянутыми панелями может вскоре сократиться благодаря постоянно совершенствующейся технологии

Тонкопленочные солнечные панели: Уникальная характеристика тонкопленочных панелей заключается в том, что в них часто используются различные материалы (кроме кремния) в производственный процесс.

Тонкопленочная солнечная панель может быть изготовлена из теллурида кадмия (CdTe), аморфного кремния (a-Si) и селенида меди-индия-галлия (CIGS) или любой такой смеси различных материалов.

Эффективность тонкопленочной солнечной панели минимальна (примерно 11%) среди трех типов солнечных панелей.

Разница между КПД и коэффициентом заполнения солнечной батареи:

Коэффициент заполнения и эффективность солнечной батареи

Эффективность

Коэффициент заполнения

я. Это отношение максимальной мощности, которую солнечная фотоэлектрическая панель может генерировать в стандартных условиях испытаний, к входной мощности

я. Это отношение максимальной мощности к теоретической мощности.

ii.

III. Вы можете максимизировать эффективность солнечной фотоэлектрической панели за счет увеличения коэффициента заполнения (FF), V _OC и I _SC .

III. Максимально достижимая мощность (теоретическая) зависит от нескольких факторов, таких как тип кремния, используемый для создания солнечных фотоэлектрических модулей. Любое отклонение коэффициента заполнения от ожидаемого может свидетельствовать о неисправности модуля.

Факторы, влияющие на эффективность фотоэлемента:

Глубокая зависимость от ископаемого топлива (уголь, нефть, природный газ и т. будущее.

Мы можем удовлетворить постоянно растущие потребности в электроэнергии с помощью альтернативного источника энергии с такими свойствами, как находчивость, долговечность и т. д.

Тотальная проверка факторов, которые могут способствовать снижению эффективности фотоэлектрических элементов. В настоящее время все более актуальным становится значение .

Давайте углубимся в влияние таких факторов-

1. Фактор заполнения: Между двумя фотоэлектрическими панелями одна с меньшей величиной коэффициента заполнения будет иметь меньшую эффективность, чем другая. один.

2. Солнечные спектры и температура: Солнечные спектры и температура влияют на эффективность фотоэлектрической панели.

Солнечная фотоэлектрическая панель вырабатывает электричество, используя солнечные лучи. Тем не менее, он снижает эффективность с увеличением освещенности.

Предположим, что температура солнечной фотоэлектрической панели превышает предел оптимальной или рабочей температуры.

В этом случае перегретая солнечная фотоэлектрическая панель вызывает падение V _OC и I _SC с последующим снижением эффективности.

3. Интенсивность света: Интенсивность света существенно влияет на коэффициент заполнения (FF). Следовательно, эффективность зависит от изменения интенсивности освещения.

ФП увеличивается при облучении менее 500 Вт/м ² (низкое облучение)
ФП уменьшается при облучении более 500 Вт/м ² (высокое облучение).

Аналогично,

Эффективность возрастает логарифмически при облучении менее 400 Вт/м ² (низкое облучение)
Тем не менее, Эффективность не снижается и не увеличивается при облучении более 400 Вт/м ² (высокое облучение).

4. Скопление пыли: Плотность скопления пыли на поверхности солнечной фотоэлектрической панели ухудшает качество и коэффициент заполнения солнечной батареи.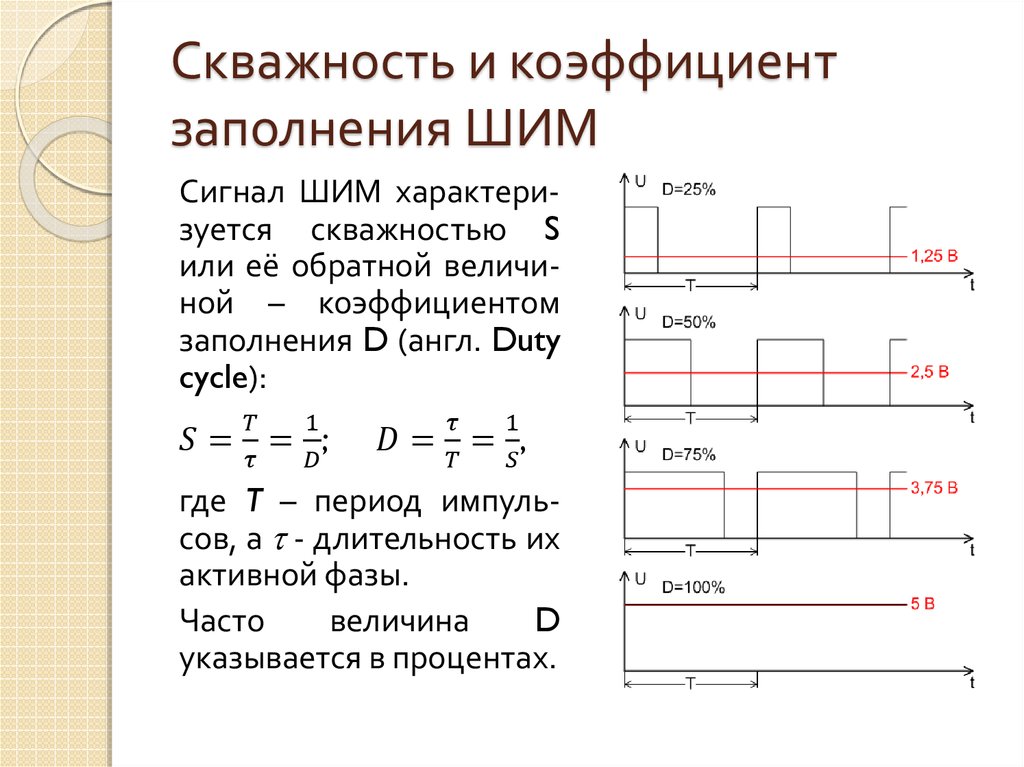

Мощность солнечного фотоэлектрического модуля может быть снижена на 20 % после одной пылевой бури и на 50 % в течение шести месяцев.

Согласно другому исследованию, в условиях тропического климата мощность фотоэлектрического модуля может быть снижена на 35 % в месяц.

Как повысить эффективность солнечной батареи:

Посмотрим правде в глаза, метод фотопреобразования солнечной фотоэлектрической панели необходимо улучшить, чтобы добиться значительного прогресса и проиллюстрировать необычайный рост в качестве альтернативного источника энергии.

Может, посмотрим, как взломать Эффективность?

Чтобы смягчить воздействие факторов окружающей среды (влажность или скопление пыли), перед установкой солнечной фотоэлектрической системы необходимо изучить соответствующее географическое положение.
Чтобы получить более значительную производительность, необходимо расширить параметры оптимизации в зависимости от различных климатических условий.
Вместо того, чтобы использовать общий метод установки солнечной фотоэлектрической системы, необходимо учитывать такие факторы, как преобладающее направление ветра или угол установки.
Поскольку эффективность солнечного элемента снижается с повышением температуры элемента (из-за термической деградации солнечного элемента), необходимо поддерживать оптимальную температуру поверхности солнечной панели.
Вы можете уменьшить явление перегрева солнечной фотоэлектрической панели с помощью методов воздушного или водяного охлаждения.
Вы можете использовать характеристики антибликового материала для улучшения характеристик солнечной фотоэлектрической панели.

Почему солнечные батареи не могут достичь 100-процентной эффективности:

Солнечные элементы не могут достичь 100% эффективности, поскольку солнечный спектр испускает фотоны с широким диапазоном энергий. Только для определенных спектральных диапазонов полупроводниковых материалов световая энергия может быть восстановлена как электрическая энергия. Теоретическая максимальная эффективность 33,7

Процесс преобразования энергии не может быть завершен на 100 % из-за внутренних резистивных или оптических потерь. Когда световая энергия отражается и рассеивается или преобразуется в ударную энергию, это препятствует полному использованию обширного источника энергии.

Окончательная мысль о коэффициенте заполнения солнечной батареи:

Глубокое понимание системы имеет решающее значение. Мы можем выбрать подходящий модуль и приложить усилия, чтобы обеспечить максимальную выработку электроэнергии от фотоэлектрической панели. Одним из способов повышения эффективности является размещение фотоэлемента в подходящем положении с учетом условий окружающей среды.

Накопление пыли приводит к снижению коэффициента заполнения солнечного элемента. Это мера того, насколько солнечный элемент действует как идеальный источник (в стандартных условиях испытаний). Ограничение скопления пыли и концентрации росы на фотоэлектрической панели повысит эффективность фотоэлектрического модуля.

Природные источники запасов энергии ограничены, а соответствующие технологии добычи угля и добычи нефти или природного газа еще предстоит реализовать. Чтобы обеспечить устойчивый и безопасный возобновляемый источник энергии сценарий, зависящий от возобновляемых источников энергии, необходим значительный запас для повышения производительности солнечных элементов.

Коэффициент заполнения солнечной батареи в фотоэлектрической панели должен быть максимальным. Интенсивно сосредоточьтесь на факторах, влияющих на эффективность солнечных батарей. Место установки должно быть лишено какой-либо затеняющей инфраструктуры. Солнечные фотоэлектрические панели должны находиться в такой среде, где невозможно плотное скопление пыли или грязи.

Ссылки:

«Влияние интенсивности освещения на параметры солнечных элементов» М. Чегаар, А. Хамзауи, А. Намода, П. Пети, М. Эллери и А. Хергут
«Влияние накопления пыли на выходную мощность солнечных фотоэлектрических модулей» Мухаммеда Дж.