Содержание
Измерение мощности в электрических цепях постоянного и переменного токов: способы и формулы
Перейти к содержанию
Search for:
На чтение 9 мин. Просмотров 7.8k. Опубликовано
Содержание
- Общие сведения
- Мощность потребителя
- Сила тока
- Электрическое напряжение
- Сопротивление электрической цепи
- Методы измерения
- Косвенный способ
- Прямое определение величины
Очень часто при проектировании электрических схем радиолюбители сталкиваются с проблемой измерения мощности, которую потребляют радиокомпоненты. Специалисты в метрологической сфере рекомендуют два метода, позволяющих вычислить и грамотно рассчитать ее значение. В этом случае нужно разобрать подробнее физический смысл величины, а также ее составляющих, от которых она зависит.
Общие сведения
При проектировании устройств нужно уметь правильно рассчитывать мощность электроэнергии электрооборудованием. Это необходимо, прежде всего, для долговечной работы устройства. Если изделие работает на износ, то оно способно выйти из строя сразу или в течение некоторого времени.
Такой вариант считается недопустимым, поскольку существуют виды техники, которые должны работать без отказов (аппарат искусственного дыхания, контроль уровня метана в шахте и так далее), так как от этого зависит человеческая жизнь. К основным характеристикам электрической энергии относятся следующие: мощность, сила тока, напряжение (разность потенциалов) и электропроводимость (сопротивление) материалов.
Мощность потребителя
Мощность не следует путать с электрической энергией. Единицей измерения первой является ватт (Вт), название которой произошло от фамилии известного физика Джеймса Уатта. Физическим смыслом 1 Вт является расход электрической энергии за единицу времени, равной 1 секунде (1 Вт = расход 1 джоуля за 1 секунду).
Ватт можно связать с некоторыми физическими величинами: 1 Вт = 1 Дж/с = (1 кг * sqr (м)) / (c * sqr (c)) = 1 Н * м / с = 746 л. с. Последнее числовое значение называется электрической лошадиной силой. Ваттметр — измеритель электрической мощности. Однако ее величину можно определить и другим способом. Для этого следует разобрать физические величины, от которых она зависит.
Сила тока
Количество электрического заряда, который проходит через токопроводящий материал за единицу времени, называется силой электрического тока. Сокращенно величину называют силой тока или током. Она обозначается литерами «I» или «i» и имеет направление (векторная величина).
Ток в научной интерпретации классифицируется на постоянный и переменный. Первый вид не изменяет своего направления за единицу времени, но его амплитудные значения могут изменяться. Направление и амплитуда переменного тока изменяется по определенному закону (синусоидальный и несинусоидальный). Основным параметром считается его частота. Определяется тип переменного тока с помощью осциллографа.
Электрическое напряжение
Из курса физики известно, что каждое вещество состоит из атомов, которые обладают нейтральным зарядом. Они состоят из субатомных частиц. К ним относятся следующие: протоны, электроны и нейтроны. Первые имеют положительный заряд, вторые — отрицательный, а третьи — не заряжены вообще.
Суммарный заряд протонов компенсирует заряд всех электронов. Однако под действием внешних сил это равенство нарушается, и электрон «вырывается» из атома, который уже обладает положительным зарядом. Он притягивает электрон с соседнего атома, и процесс повторяется до тех пор, пока энергия не будет минимальной (меньше энергии «вырывания» электрона).
При межатомном взаимодействии образуется электромагнитное поле с отрицательной или положительной составляющими. Разность между двумя точками противоположных по знаку составляющих называется электрическим напряжением. Работа электромагнитного поля по перемещению точечного электрического заряда из точки А в точку В называется разностью потенциалов. Физический смысл напряжения (U): разность потенциалов в 1 В между двумя точечными зарядами в 1 Кл, на перемещение которых тратится энергия электромагнитного поля, равная 1 Дж.
Единицей измерения является вольт (В). Определить значение разности потенциалов можно с помощью вольтметра, который подключается параллельно. Производными единицами измерения считаются следующие: 1 мВ = 0,001 В, 1 кВ = 1000 В, 1 МВ = 1000 кВ = 1000000 В и так далее.
Сопротивление электрической цепи
Электропроводимость материала зависит от нескольких факторов: электронной конфигурации, типа вещества, геометрических параметров и температуры.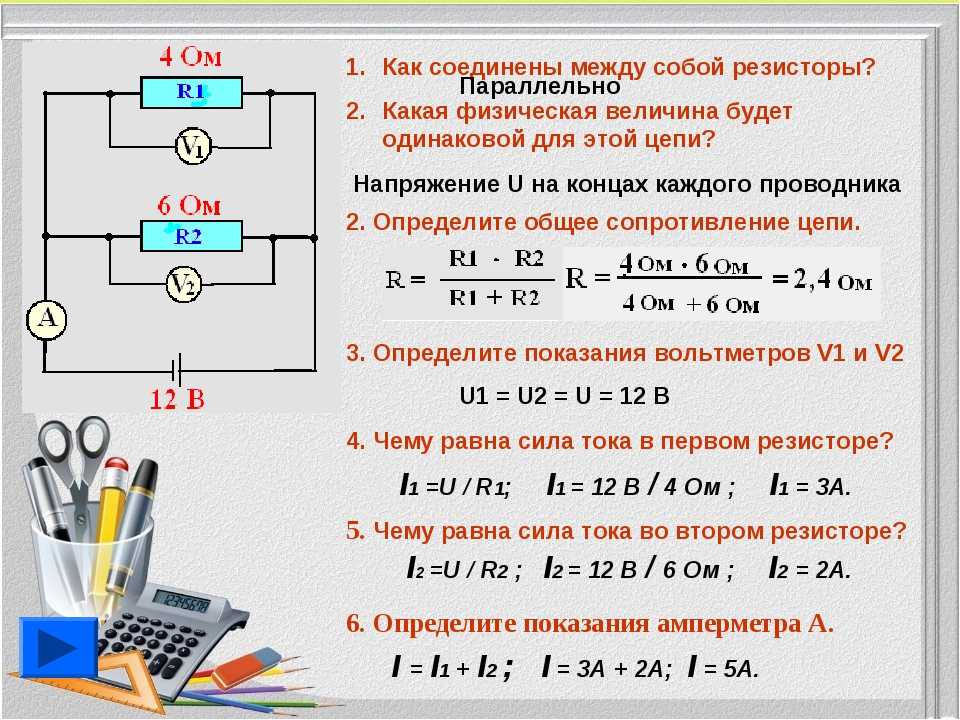
- Проводниками.
- Полупроводниками.
- Диэлектриками.
К первой группе следует отнести все металлы, электролиты (растворы, проводящие ток) и ионизированные газы. Носителями электрического заряда в металлах являются электроны. В растворах их роль выполняют ионы, которые бывают положительными (анионы) и отрицательными (катионы). Свободными носителями заряженных частиц в газах считаются свободные электроны и положительно заряженные ионы.
Полупроводники проводят электричество только при определенных условиях. Например, при воздействии на него внешних сил. Под их действием кулоновские связи электрона с ядром уменьшаются. При этом отрицательно заряженная частица «вырывается». На ее месте образуется «дырка», обладающая положительным зарядом. Она притягивает соседний электрон, вырывая его с атома.
В проводниках при повышении температурных показателей происходит рост величины сопротивления. При этом происходит разрушение и искажение кристаллической решетки. Заряженные частицы сталкиваются (взаимодействуют) с атомами и другими частицами материала. В результате их движение замедляется, но потом снова возобновляется под действием электромагнитного поля. Процесс этого «взаимодействия» называется электрической проводимостью вещества. Однако в полупроводниках при повышении температуры эта величина уменьшается. К геометрии материалов следует отнести следующие: длину и площадь поперечного сечения.
Сопротивление измеряется в Омах (Ом) при помощи омметра, который подсоединяется параллельно к участку цепи или радиодетали. Существуют производные единицы измерения: 1 кОм = 1000 Ом, 1 МОм = 1000 кОм = 1000000 Ом.

Методы измерения
Мощность можно определить двумя способами: косвенным и прямым. В первом случае это делается при помощи амперметра и вольтметра, а также осциллографа. Измеряются значения напряжения и тока, а затем по формулам вычисляется мощность. Этот способ имеет один недостаток: величина мощности получается с некоторой погрешностью.
При использовании прямого метода используется специальный прибор-измеритель. Он называется ваттметром и показывает мгновенное значение мощности. У каждого из способов есть свои достоинства и недостатки. Какой из методов наиболее оптимален, определяет сам радиолюбитель. Если проектируется какое-либо изделие, которое отличается надежностью, то следует применять прямой метод. В других случаях рекомендуется воспользоваться косвенным методом.
Косвенный способ
Мощность в цепях постоянного и переменного токов определяется различными способами.
Для цепей постоянного тока нужно воспользоваться формулой: P = U * I. Ее можно вывести из закона Ома для участка или полной цепи. Если рассматривается полная цепь, то формула принимает другой вид с учетом ЭДС (е): P = e * I. Основные соотношения для расчета:
- Для участка электрической цепи: P = I * I * R = U * U / R.
- Для полной цепи, в которой подключен электродвигатель или выполняется зарядка аккумулятора (потребление): P = I * e = I * e — sqr (I) * Rвн = I * (e — (I * Rвн)).
- В цепи присутствует генератор или гальванический элемент (отдача): P = I * (e + (I * Rвн)).
Эти соотношения невозможно применять для цепей переменного тока, поскольку он подчиняется другим физическим законам. При измерении мощности в цепях переменного тока следует учитывать ее составляющие (активная, реактивная и полная).
Для вычисления первого типа физической величины применяется формула такого вида: Ра = I * U * cos (a). Значения тока и напряжения являются среднеквадратичными, а cos (a) — косинус угла между ними. Для определения реактивной мощности нужно воспользоваться следующей формулой: Qр = I * U * sin (a). Если нагрузка в цепи является индуктивной, то значение будет больше 0. В противном случае — меньше 0. Полная мощность Р определяется по следующему соотношению: P = Pa + Qp.
Прямое определение величины
Для определения значения мощности в цепях переменного и постоянного тока применяются ваттметры. В них используются электродинамические или ферроидальные механизмы. Приборы с электродинамическим механизмом выпускаются в виде переносных приборов.
Ферродинамические приборы изготавливаются в виде электронных узлов, которые вставляются в измерительные стенды или щитовые. Основное их назначение — контроль приблизительных параметров потребления мощности электрооборудованием. Они обладают низким классом точности и применяются для измерения значений мощности переменного тока. При постоянном токе погрешность увеличивается, поскольку это обусловлено искажением петли гистерезиса ферромагнитных сердечников.
По диапазону частот приборы можно разделить на две группы: низкочастотные и радиочастотные. Ваттметры низких частот применяются в сетях промышленного питания переменного тока. Радиочастотный тип рекомендуется применять для точных измерений при проектировании различной техники. Они делятся на две категории по мощности:
- Проходящие.
- Поглощающие.
Первый вид подключается в разрыв линии, а второй — в ее конец в качестве нагрузки согласования. Кроме того, приборы для измерения мощности бывают аналоговыми и цифровыми.
При измерении мощности на высоких частотах применяются электронные и термоэлектронные ваттметры. Главным узлом считается микроконтроллер и преобразователь активной мощности. Последний преобразовывает переменный ток в постоянный. После этого происходит перемножение в микроконтроллере силы тока и напряжения. Результатом является сигнал на выходе, который зависит от I и U.
Ваттметр состоит из двух катушек. Первая из них подключается последовательно в цепь нагрузки, а другая (подвижная с резистором) — параллельно. В цифровых моделях роль катушек выполняют датчики тока и напряжения. Прибор имеет две пары зажимов. Одна пара применяется для последовательной цепи, а другая — для параллельной. Для правильного включения ваттметра выполняется обозначение * одной из двух пар зажимов.
Таким образом, для измерения мощности электрического тока применяются два метода. Первый из них является косвенным, а второй — прямым. Последний рекомендуется применять при проектировании сложной техники.
Adblock
detector
Мощность электрического тока: особенности и измерения
Содержание
- 1 Работа электрического тока, мощность
- 2 Трехфазные цепи
- 3 На практике измерить мощность тока
Мощность электрического тока – скорость выполняемой цепью работы. Простое определение, морока с пониманием. Мощность подразделяется на активную, реактивную. И начинается…
Работа электрического тока, мощность
При движении заряда по проводнику поле выполняет над ним работу. Величина характеризуется напряжением, в отличие от напряженности в свободном пространстве.
Электрическая дуга
На схеме момент превращения энергии отображается в виде источников ЭДС. Если у генераторов направлены в одну сторону, у потребителя – обязательно в другую. Наглядным фактом отражается процесс расхода мощности, отбора у источников энергии. ЭДС несет обратный знак, часто называется противо-ЭДС. Избегайте путать понятие с явлением, возникающим в индуктивностях при выключении питания. Противо-ЭДС означает переход электрической энергии в химическую, механическую, световую.
Потребитель хочет выполнить работу за некоторую единицу времени. Очевидно, газонокосильщик не намерен ждать зимы, надеется управиться к обеду.
Полезная работа на физических схемах обозначается противо-ЭДС (обычный источник с обратным генератору направлением). Для мощности имеется несколько аналитических выражений. Иногда удобно использовать одно, в других случаях – иное (см. рис.):
Выражения мощности тока
- Мощность – скорость выполнения работы.
- Мощность равна произведению напряжения на ток.
- Мощность, затрачиваемая на тепловое действие, равна произведению сопротивления на квадрат тока.
- Мощность, затрачиваемая на тепловое действие, равна отношению квадрата напряжения к сопротивлению.
Запасшемуся токовыми клещами проще использовать вторую формулу. Вне зависимости от характера нагрузки посчитаем мощность. Только активную. Мощность определена многими факторами, включая температуру. Под номинальным для прибора значением понимаем, развиваемое в установившемся режиме. Для нагревателей следует применять третью, четвертую формулу. Мощность зависит целиком и полностью от параметров питающей сети. Предназначенные для работы со 110 вольт переменного тока в европейских условиях быстро сгорят.
Трехфазные цепи
Новичкам трехфазные цепи представляются сложными, на деле это более элегантное техническое решение. Даже электричество домом поставляют тремя линиями. Внутри подъезда делят по квартирам. Больше смущает то, что некоторые приборы на три фазы лишены заземления, нулевого провода. Схемы с изолированной нейтралью. Нулевой провод не нужен, ток возвращается источнику по фазным линиям. Разумеется, нагрузка здесь на каждую жилу повышенная. Требования ПУЭ отдельно оговаривают род сети.
Трехфазная цепь с изолированной нейтралью
- Фазным напряжением, током называют, соответственно, разницу потенциалов и скорость передвижения заряда меж фазой и нейтралью. Понятно, в оговоренном выше случае с полной изоляцией формулы будут недействительны. Поскольку нейтрали нет.
- Линейным напряжением, током называют, соответственно, разницу потенциалов или скорость перемещения заряда меж любыми двумя фазами. Номера понятны из контекста. Когда говорят о сетях 400 вольт, подразумевают три провода, разница потенциалов с нейтралью равна 230 вольт. Линейное напряжение выше фазного.
Меж напряжением и током существует сдвиг фаз. О чем умалчивает школьная физика. Фазы совпадают, если нагрузка 100% активная (простые резисторы). Иначе появляется сдвиг. В индуктивности ток отстает от напряжения на 90 градусов, в емкости – опережает. Простая истина легко запоминается следующим образом (плавно подходим к реактивной мощности).
Из равенства видно: напряжение нужно отложить вверх на 90 градусов при построении диаграммы, ток останется на оси абсцисс (горизонтальная ось Х). Вращение по правилам радиотехники происходит против часовой стрелки. Теперь очевиден факт: ток отстает на 90 градусов. По аналогии проведем сравнение для конденсатора. Сопротивление переменному току в мнимой форме выглядит так: -j/ωL, знак указывает: откладывать напряжение нужно будет вниз, перпендикулярно оси абсцисс. Следовательно, ток опережает по фазе на 90 градусов.
В реальности параллельно с мнимой частью присутствует действительная – называют активным сопротивлением. Проволока катушки представлена резистором, будучи свитой, приобретает индуктивные свойства. Поэтому реальный угол фаз будет не 90 градусов, немного меньше.

А теперь можно переходить к формулам мощности тока трехфазных цепей. Здесь линия формирует сдвиг фаз. Меж напряжением и током, и относительно другой линии. Согласитесь, без заботливо изложенных авторами знания факт нельзя осознать. Меж линиями промышленной трехфазной сети сдвиг 120 градусов (полный оборот – 360 градусов). Обеспечит равномерность вращения поля в двигателях, для рядовых потребителей безразличен. Так удобнее генераторам ГЭС – нагрузка сбалансированная. Сдвиг идет меж линиями, в каждой ток опережает напряжение или отстает:
- Если линия симметричная, сдвиги меж любыми фазами по току составляют 120 градусов, формула получается предельно простой. Но! Если нагрузка симметрична. Посмотрим изображение: фаза ф не 120 градусов, характеризует сдвиг меж напряжением и током каждой линии. Предполагается, включили двигатель с тремя равноценными обмотками, получается такой результат. Если нагрузка несимметрична, потрудитесь провести вычисления для каждой линии отдельно, затем сложить результаты воедино для получения общей мощности тока.
- Вторая группа формул приведена для трехфазных цепей с изолированной нейтралью. Предполагается, ток одной линии утекает по другой. Нейтраль отсутствует за ненадобностью. Поэтому напряжения берутся не фазные (не от чего отсчитывать), как предыдущей формулой, а линейные. Соответственно, цифры показывают, какой параметр следует взять. Повремените пугаться греческих букв – фазы меж двумя перемножаемыми параметрами. Цифры меняются местами (1,2 или 2,1), чтобы правильно учесть знак.
- В асимметричной цепи вновь появляются фазные напряжение, ток. Здесь расчет ведется отдельно для каждой линии. Никаких вариантов нет.
Формулы мощности тока
На практике измерить мощность тока
Намекнули, можно воспользоваться токовыми клещами. Прибор позволит определить крейсерские параметры дрели. Разгон можно засечь только при многократных опытах, процесс чрезвычайно быстрый, частота смены индикации не выше 3-х раз в секунду. Токовые клещи демонстрируют погрешность. Практика показывает: достичь погрешности, указанной в паспорте, сложно.
Чаще для оценки мощности используют счетчики (для выплат компаниям-поставщикам), ваттметры (для личных и рабочих целей). Стрелочный прибор содержит пару неподвижных катушек, по которым течет ток цепи, подвижную рамку, для заведения напряжения путем параллельного включения нагрузки. Конструкция рассчитана сразу реализовать формулу полной мощности (см. рис.). Ток умножается на напряжение и некий коэффициент, учитывающий градуировку шкалы, также на косинус сдвига фаз между параметрами. Как говорили выше, сдвиг умещается в пределах 90 – минус 90 градусов, следовательно, косинус положителен, крутящий момент стрелки направлен в одну сторону.
Отсутствует возможность сказать индуктивная ли нагрузка или емкостная. Зато при неправильном включении в цепь показания будут отрицательными (завал набок). Произойдет аналогичное событие, если потребитель вдруг станет отдавать мощность обратно нагрузке (бывает такое). В современных приборах происходит нечто подобное же, вычисления ведет электронный модуль, интегрирующий расход энергии, либо считывающий показания мощности.
Особые проблемы вызывают измерения в асимметричных цепях с изолированной нейтралью, где нельзя прямо складывать мощности каждой линии. Ваттметры делятся принципом действия:
- Электродинамические. Описаны разделом. Состоят из одной подвижной, двух неподвижных катушек.
- Ферродинамические. Напоминает двигатель с расщепленным полюсом (shaded-pole motor).
- С квадратором. Используется амплитудно-частотная характеристика нелинейного элемента (например, диода), напоминающая параболу, для возведения электрической величины в квадрат (используется в вычислениях).
- С датчиком Холла. Если индукцию сделать при помощи катушки пропорциональной напряжению магнитного поля в сенсоре, подать ток, ЭДС будет результатом умножения двух величин. Искомая величина.
- Компараторы.
Постепенно повышает опорный сигнал, пока не будет достигнуто равенство. Цифровые приборы достигают высокой точности.
В цепях с сильным сдвигом фаз для оценки потерь применяется синусный ваттметр. Конструкция схожа с рассмотренной, пространственное положение таково, что вычисляется реактивная мощность (см. рис.). В этом случае произведение тока и напряжения домножим на синус угла сдвига фаз. Реактивную мощность измерим обычным (активным) ваттметром. Имеется несколько методик. Например, в трехфазной симметричной цепи нужно последовательную обмотку включить в одну линию, параллельную – в две другие. Затем производятся вычисления: показания прибора умножаются на корень из трех (с учетом, что на индикаторе произведение тока, напряжения и синуса угла между ними).
Методика двух ваттметров
Для трехфазной цепи с простой асимметрией задача усложняется. На рисунке показана методика двух ваттметров (ферродинамических или электродинамических). Начала обмоток указаны звездочками.
Основы измерения электрической мощности
Основные измерения электрической мощности
Понимание производства электроэнергии, потери мощности и различных типов измеряемой мощности может быть пугающим. Ниже приведен обзор основных измерений электрической и механической мощности.
Электрический ток, напряжение и сопротивление
Любое обсуждение электричества неизбежно приводит к электрическому току, напряжению и сопротивлению. Эти концепции показаны ниже на рисунке 1. Электрический ток представляет собой поток самого электричества и измеряется в единицах, называемых амперами (А). Напряжение — это сила, которая заставляет электричество течь, и измеряется в единицах, называемых вольтами (V или U).
На рисунке ниже эти отношения показаны в виде электрических цепей. В электрической цепи электрический ток проходит через различные типы нагрузки, включая сопротивление, индуктивность и емкость, от положительной полярности источников питания, таких как батареи, а затем возвращается к отрицательной полярности источника питания. Термин «нагрузка» обычно используется для обозначения чего-то, что получает электричество от источника питания и работает (обеспечивает свет, в случае лампочки).
Рисунок 1 – Основные компоненты электрической цепиМощность
Электрическая энергия может быть преобразована в другие формы энергии и использована. Например, его можно преобразовать в тепло в электронагревателе, в крутящий момент в двигателе или в свет в люминесцентной или ртутной лампе. В подобных примерах работа, совершаемая электричеством за определенный период времени (или затрачиваемая электрическая энергия), называется электрической мощностью.
В электрических системах напряжение — это сила, необходимая для перемещения электронов. Ток — это скорость потока заряда в секунду через материал, к которому приложено определенное напряжение. Взяв напряжение и умножив его на соответствующий ток, можно определить мощность.
Мощность постоянного тока (постоянного тока)
Постоянный ток или постоянный ток относится к системам питания, в которых используется одна полярность напряжения и тока, однако амплитуда может изменяться (циклически или случайным образом).
Рисунок 2. Базовая схема, показывающая напряжение и ток с источником постоянного напряжения электрический ток, напряжение и сопротивление. Закон Ома гласит, что электрический ток течет пропорционально напряжению. Ниже показана формула для выражения отношения между током (I) и напряжением (U).
По этой формуле ток (I) уменьшается с увеличением значения R и, наоборот, ток (I) увеличивается с уменьшением значения R. R здесь представляет собой сопротивление (или электрическое сопротивление). Другими словами, мы видим, что по мере увеличения или уменьшения сопротивления (R) ток течет с меньшей или большей легкостью. Эту формулу можно переписать, как показано ниже. Если известны два значения тока, напряжения и сопротивления, можно получить оставшееся значение.
Мощность постоянного тока (DC) P (Вт) определяется путем умножения приложенного напряжения (U) на ток I (А), как показано выше. В приведенном ниже примере количество электроэнергии, определяемое предыдущим уравнением, извлекается из источника питания и потребляется сопротивлением R (в омах) каждую секунду. По закону Ома мы можем переписать формулу следующим образом:
Электрические цепи постоянного тока поддерживают постоянный ток и напряжение без циклических изменений. Таким образом, очень просто получить мощность постоянного тока (P) с результирующей формой волны, показанной ниже.
Источник переменного тока (AC)
Источник питания, обычно используемый в Японии, работает при напряжении 100 В переменного тока. Эти 100 В представляют собой напряжение, выраженное как среднеквадратичное значение (среднеквадратичное значение).
Напряжение 100 В от настенных розеток выглядит как чистые синусоидальные волны, как показано на рисунке ниже. Мы можем видеть, что полярность меняется циклами, и что напряжения постоянно колеблются. Формы сигналов напряжения переменного тока имеют чистые синусоидальные волны, такие как график на рис. 3, а также множество других волн, таких как искаженные волны, такие как обычные формы, такие как треугольная и прямоугольная волна. Чтобы установить размер этих волн переменного тока и напряжения, нам нужны значения, которые используют тот же стандарт. Поэтому используется среднеквадратичное значение (rms), которое было установлено на основе постоянного тока и напряжения.
Рисунок 3. Изменение полярности переменного напряжения в синусоидальных, треугольных и прямоугольных волнах
Изменение полярности переменного напряжения в синусоидальных, треугольных и прямоугольных волнах
Среднеквадратичное значение (среднеквадратичное значение)
Среднеквадратичное значение чаще всего используется при выражении значений переменного тока и напряжения, и измеряется в Arms и Urms. В приведенном выше примере 100 В — это напряжение, выраженное как среднеквадратичное значение (среднеквадратичное значение).
Простое среднее значение синусоиды равно нулю, поэтому требуется другое уравнение. Вот почему используется среднеквадратичное значение (rms), которое было установлено на основе постоянного тока и напряжения. Он основан на количестве работы, выполняемой определенным количеством постоянного тока и напряжения, и выражает, используя те же значения, что и для постоянного тока и напряжения, величину переменного тока и напряжения, которые совершают тот же объем работы.
Если теплотворная способность при подаче напряжения постоянного тока на резистор такая же, как теплотворная способность при подаче переменного тока другой формы волны, то среднеквадратичное значение напряжения переменного тока равно значению напряжения постоянного тока.
Например, теплотворная способность при подаче постоянного напряжения 100 В на резистор 10 Ом такая же, как теплотворная способность при подаче на тот же резистор переменного тока 100 В. Понятие среднеквадратичного значения то же самое для электрического тока.
Рис. 4. Равная теплотворная способность сигналов постоянного и переменного тока
Теплотворная способность относится к количеству выполненной работы, поэтому следующая формула рассчитывает мощность как теплотворную способность.
В качестве примера на следующей диаграмме показаны колебания мощности в зависимости от времени при подаче постоянного тока 1 A и переменного тока 1 ампер на резистор 10 Ом.
Рис. 5. Зависимость мощности от времени при постоянном и переменном токе
Поскольку при постоянном токе нет колебаний значения тока, значение мощности остается постоянным и составляет 10 Вт. Однако, поскольку значение тока постоянно колеблется при переменном токе, значение мощности колеблется со временем.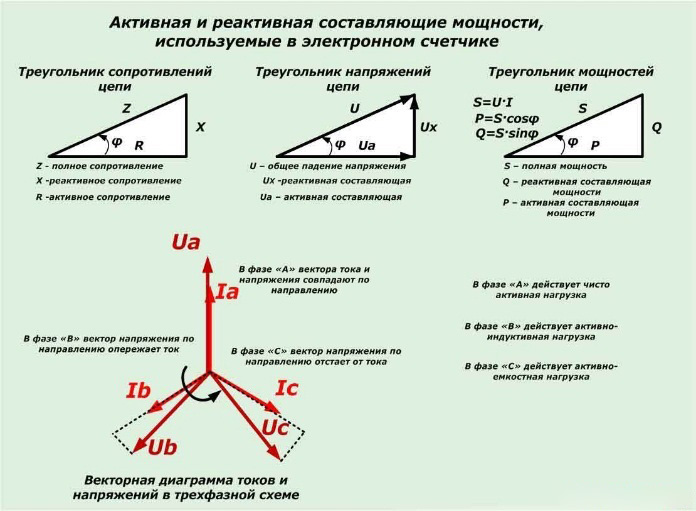
Здесь резистор (R) постоянный, поэтому им можно пренебречь. Следующее выражает результирующую связь между постоянным током и переменным током.
Если максимально уменьшить интервал между I1 и In в этой формуле, в конечном итоге Irms дает квадратный корень из площади части, заключенной в сигнале, деленный на время. Это выражается в виде формулы ниже.
Важно знать, что постоянный ток силой 1 А выполняет такую же работу, что и переменный среднеквадратичный ток силой 1 ампер. При постоянном и устойчивом постоянном токе вы можете получить значение мощности, просто умножив ток на напряжение.
Однако переменный ток не так прост, как постоянный, из-за разности фаз между током и напряжением. Ниже приведены три типа переменного тока. Как правило, мощность и потребляемая мощность относятся к активной мощности.
Мощность в системах переменного тока
Как и в случае постоянного тока, значение мощности (мгновенное значение мощности) в определенный момент времени для переменного тока можно получить путем умножения напряжения и тока для этого момента времени.
При переменном токе, поскольку и ток, и напряжение циклически колеблются, значения мощности также постоянно колеблются. Это показано на следующей диаграмме.
В качестве энергии в секунду мощность может быть получена из среднего значения мгновенной энергии, т. е. площади части, заключенной в форму волны, по времени. Формула выглядит следующим образом:
Например, если к резистору приложен ток 1 ампер и напряжение 100 ампер, как показано ниже, мощность становится равной 100 Вт при расчете по приведенной выше формуле.
При подаче тока и напряжения на резистор результирующие формы сигналов показаны на рис. 6 ниже.
Рис. 6. Отсутствие разности фаз при чисто резистивной нагрузке
6. Отсутствие разности фаз при чисто резистивной нагрузке
Говорят, что ток и напряжение находятся «в фазе» по полярности и времени, когда кривые тока и напряжения проходят через нуль. Ток и напряжение всегда совпадают по фазе, когда нагрузка состоит только из сопротивления.
Когда нагрузка имеет катушку в дополнение к сопротивлению, возникает фазовый сдвиг между сигналами напряжения и тока. Это отставание называется разностью фаз и показано на рис. 7.9.0007
Рисунок 7. Разность фаз, характерная для индуктивной и емкостной нагрузки
Разность фаз обычно выражается как Φ (фи), а единицей измерения являются радианы, но часто указывается в градусах. В приведенном ниже примере точка A начинается с точки P и совершает один оборот по окружности O. Расстояние между точкой A и прямой линией, проходящей через центр O и точку P (красная линия) в качестве оси Y и ∠AOP (φ), так как ось X приводит к синусоидальной волне ниже.
Рис. 8. Синусоидальная волна показана с фазой
8. Синусоидальная волна показана с фазой
На Рис. 9 показаны формы тока и напряжения, сдвинутые по фазе на 60°. При рассмотрении положения на окружности напряжения (u) и тока (i) в соответствии с приведенным выше примером ∠uoi постоянна в каждый момент времени. Угол этого ∠uoi указывает размер разности фаз между напряжением (u) и током (i).
Рис. 9. Синусоиды напряжения и тока с разностью фаз
Три типа нагрузки цепи переменного тока показаны на рис. 10. Как показано ниже, разность фаз между током и напряжением возникает в зависимости от типа нагрузки.
Рисунок 10. Фазное и векторное представление цепей переменного тока с резистивной, индуктивной или емкостной нагрузкой С фазами ток может отставать по отношению к напряжению или опережать его. Ток отстает на 90⁰, когда нагрузка состоит только из индуктивности, и опережает на 90⁰, когда только емкость. Когда существуют все три типа, разность фаз колеблется в соответствии с соотношением размеров каждого компонента.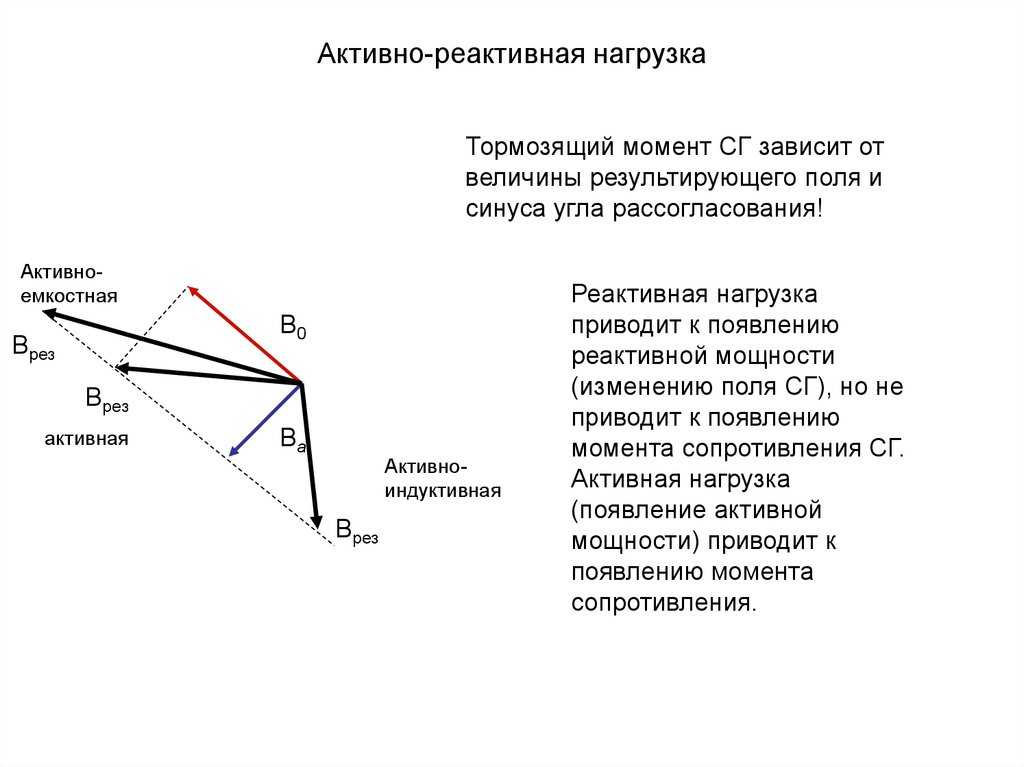
Мощность переменного тока с разницей фаз
При наличии разности фаз между током и напряжением происходит мгновенное изменение энергии, как показано на рисунке 11.
Когда ток или напряжение равны 0, мгновенная мощность становится равной 0. полярность напряжения меняется в промежутках между ними, мгновенная мощность становится отрицательной. Мощность представляет собой среднее значение мгновенной энергии, поэтому мощность становится меньше, чем когда ток и напряжение совпадают по фазе (пунктирная линия).
Рисунок 11. Мгновенная энергия, когда напряжение и ток имеют разность фаз
Треугольник мощности и коэффициент мощности
Цепи переменного тока, содержащие емкость, индуктивность или и то, и другое, содержат активную и реактивную мощности. Треугольник мощности, показанный на рис. 12, помогает проиллюстрировать энергопотребление в индуктивной или емкостной цепи.
Активная мощность
Активная мощность (P) — это реальная мощность, которую устройство потребляет и выполняет реальную работу в электрической цепи. Активная мощность рассчитывается ниже в ваттах (Вт).
Реактивная мощность
Реактивная мощность (Q) — это мощность, которая не потребляется устройством и передается туда и обратно между источником питания и нагрузкой. Иногда называемая безваттной мощностью, реактивная мощность забирает мощность из цепи из-за фазового сдвига, создаваемого емкостными и/или индуктивными компонентами. Этот фазовый сдвиг уменьшает количество активной мощности для выполнения работы и усложняет расчет мощности.
Полная мощность
Полная мощность (S) представляет собой гипотенузу треугольника мощности, состоящего из сложения векторов активной мощности (P) и реактивной мощности (Q). Расчет полной мощности представляет собой произведение среднеквадратичного значения напряжения на среднеквадратичное значение тока в вольт-амперах (ВА).
Коэффициент мощности
При определении коэффициента мощности для синусоидальных волн коэффициент мощности равен косинусу угла между напряжением и током (Cos Φ). Он определяется как коэффициент мощности «смещения» и верен только для синусоидальных волн. Для всех других форм сигналов (не синусоидальных волн) коэффициент мощности определяется как мощность в ваттах, деленная на полную мощность в амперах напряжения. Это называется «истинным» коэффициентом мощности и может использоваться для всех форм сигналов, как синусоидальных, так и несинусоидальных, с использованием квалификатора λ (лямбда).
Коэффициент мощности (λ) увеличивается или уменьшается в зависимости от величины разности фаз (φ). Рисунок 13 иллюстрирует это явление. Рис. 13. Коэффициент мощности с различной разностью фаз разность фаз увеличивается; коэффициент мощности равен 0,5 (активная мощность составляет 1/2 полной мощности) при разности фаз 60⁰ и 0 при разнице фаз 90⁰. Коэффициент мощности 0 означает, что ток течет к нагрузке, но она не совершает никакой работы.
Векторное отображение переменного тока
Смещение по времени между напряжением и током называется разностью фаз, а Φ — фазовым углом. Смещение по времени в основном вызвано нагрузкой, на которую подается питание. В общем, разность фаз равна нулю, когда нагрузка является чисто резистивной. Ток отстает от напряжения, когда нагрузка индуктивная. Ток опережает напряжение, когда нагрузка емкостная.
Рис. 14. Смещение фаз между напряжением и током при чисто индуктивной или емкостной нагрузке
Векторное отображение используется для четкой передачи зависимости величины и фазы между напряжением и током.
Системы питания переменного тока
Электропитание переменного тока может быть однофазным или многофазным. Однофазное электричество используется для питания обычных бытовых и офисных электроприборов, но для распределения электроэнергии и подачи электроэнергии непосредственно на оборудование большей мощности почти повсеместно используются трехфазные системы переменного тока.
Схемы однофазной проводки
Для однофазных цепей существуют две распространенные конфигурации проводки. Наиболее распространена однофазная двухпроводная схема. Другая — однофазная трехпроводная схема, обычно встречающаяся в бытовых приборах.
Однофазная 2-проводная система (1P2W)
Обеспечивает подачу однофазного переменного тока с использованием двух проводников.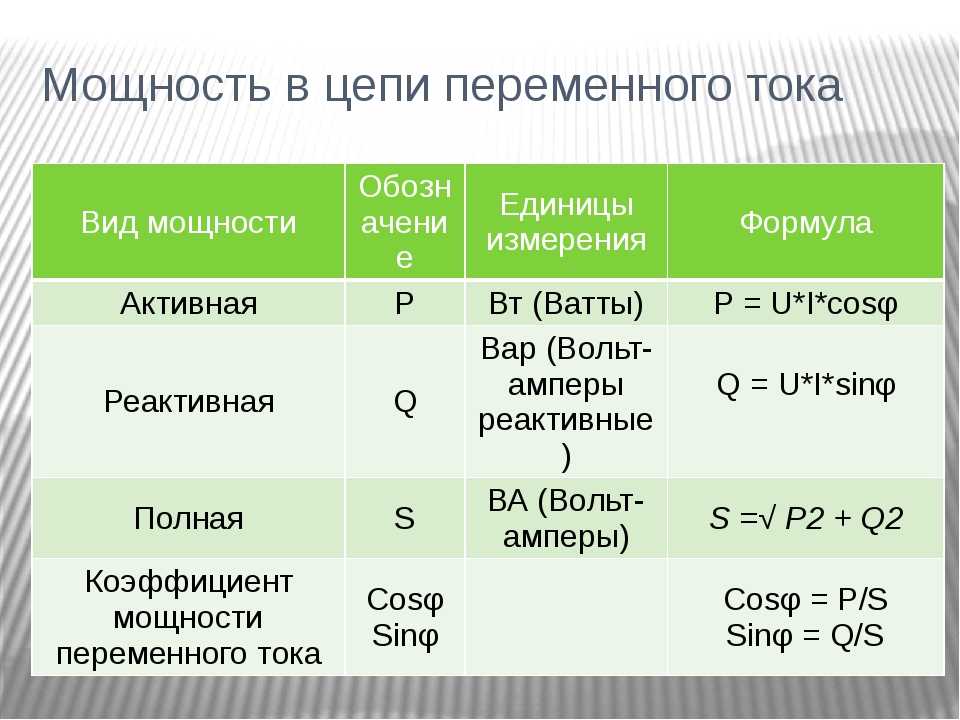
Влияние паразитной емкости
При измерении однофазного устройства влияние паразитной емкости на точность измерения можно свести к минимуму, подключив клемму токового входа прибора к стороне, наиболее близкой к потенциалу земли источника питания. Рисунок 17. Схема подключения для минимизации паразитной емкости Когда измеренный ток относительно мал, подключите клемму измерения тока между клеммой измерения напряжения и нагрузкой.
Рис. 18. Схема подключения при относительно большом измеряемом токе
Двухфазная трехпроводная система (1P3W)
Обеспечивает однофазное питание переменного тока с использованием трех проводников.
Схемы подключения трехфазной сети
В отличие от однофазных систем, по проводникам трехфазного источника питания течет переменный ток одинаковой частоты. и амплитуда напряжения относительно общего эталона, но с разницей фаз в одну треть периода. Трехфазные системы имеют преимущества перед однофазными, которые делают их пригодными для передачи энергии и в таких приложениях, как асинхронные двигатели.
Характеристики трехфазных систем
- Ток и напряжение на каждой фазе имеют разность фаз 120° в сбалансированной системе.
- Линейное напряжение — это напряжение, измеренное между любыми двумя линиями в трехфазной цепи.
- Фазное напряжение — это напряжение, измеренное на нагрузке в фазе
- Линейный ток — это ток в любой одной линии между трехфазным источником и нагрузкой.
- Фазный ток – это ток через любой компонент, состоящий из трехфазного источника или нагрузки.
- При соединении треугольником линейное напряжение совпадает с фазным напряжением. Для синусоидальных волн линейный ток в √3 раза превышает фазный ток.
- При соединении звездой линейное напряжение в √3 раза превышает фазное напряжение, а токи одинаковы.
- Трехфазные источники питания могут передавать в три раза больше энергии, используя всего в 1,5 раза больше проводов, чем однофазные источники питания (т. е. три вместо двух). Таким образом, отношение емкости к материалу проводника удваивается.
- Трехфазные системы также могут создавать вращающееся магнитное поле с заданным направлением и постоянной величиной, что упрощает конструкцию электродвигателей.
До сих пор в обсуждении источник питания и нагрузка были соединены двумя проводниками.
На диаграммах на рис. 20 показаны источник и нагрузка в конфигурации «треугольник» или «звезда» (звезда).
Рис. 20. Трехфазные конфигурации «треугольник» и «звезда» (WYE)
Теорема Блонделя
необходимы для наиболее точного измерения. Теорема утверждает, что мощность, подводимая к системе из N проводников, равна алгебраической сумме мощностей, измеренных N ваттметрами. Кроме того, если общая точка расположена на одном из проводников, то счетчик этого проводника может быть удален и требуется только N-1 счетчиков.
Трехфазное соединение звездой (3P4W)
Измерение относительно простое, если объектом измерения является трехфазная 4-проводная система.
Полная мощность, активная мощность и реактивная мощность для трехфазной мощности представляют собой сумму каждой фазы.
Трехфазный ваттметр Delta Two (3P3W)
Измерение в трехфазной 3-проводной системе немного сложнее, поскольку нейтральный проводник использовался в качестве основы для трехфазной 4-проводной системы. система отсутствует и фазное напряжение не может быть измерено. Измерение в трехфазной трехпроводной системе включает получение значения трехфазной мощности переменного тока с использованием метода, называемого методом двух ваттметров.
Применяя теорему Блонделя и используя метод двух ваттметров, мы можем получить значения трехфазной мощности переменного тока. Схема подключения для метода двух ваттметров и векторная карта приведены ниже.
Вывод теоремы Блонделя приведен ниже.
Расчеты, приведенные выше, показывают, что мы можем получить значения трехфазной мощности переменного тока из двухлинейных значений мощности и двухфазных значений тока. Поскольку этот метод требует контроля только двух токов и двух напряжений вместо трех, упрощается установка и конфигурация проводки. Он также может точно измерять мощность в сбалансированной или несбалансированной системе. Его гибкость и недорогая установка делают его подходящим для производственных испытаний, в которых требуется измерение только мощности или нескольких других параметров.
Другими словами, для трехфазного измерения мощности мощность может быть получена путем измерения мощности для каждой фазы и расчета общей мощности.
Трехфазное соединение треугольником (3V3A)
Существует еще один метод измерения в трехфазной трехпроводной системе: трехфазное трехфазное измерение (3V3A). Как и метод двух ваттметров, этот метод измеряет ток фазы T и линейное напряжение между R и S. Ниже представлена схема подключения.
Рисунок 22. Трехфазное соединение треугольником (3V3A)
Поскольку метод трехфазного трехтока (3V3A) измеряет ток фазы T, он позволяет увидеть баланс токов между фазами, что было невозможно при использовании метод двух ваттметров. Для инженерных и научно-исследовательских и опытно-конструкторских работ лучше всего подходит трехфазный
трехпроводный с трехваттметровым методом, так как он дает дополнительную информацию, которую можно использовать для балансировки нагрузки и определения истинного коэффициента мощности. В этом методе используются все три напряжения и все три тока.
Векторное отображение измерений трехфазного переменного тока
Мы будем использовать трехфазную систему Y «звезда», чтобы проиллюстрировать концепцию трехфазного векторного отображения. В звездной системе напряжения и токи каждой фазы смещены на 120°. Нейтральная точка Y-системы находится в центре, где теоретически сумма всех напряжений и токов равна нулю.
При проведении измерений в звездной системе, где присутствует физический нейтральный провод; напряжения будут измеряться относительно этой нейтральной точки, это называется «фазным напряжением». При проведении измерений в звездной системе, где отсутствует физический нейтральный провод; напряжения будут измеряться относительно друг друга, это называется «линейное напряжение» или «соединение треугольником». Схема соединения треугольником образует равносторонний треугольник с интервалом между напряжениями 60 градусов, в отличие от соединения звезды, где напряжение изменяется на 120 градусов.
Измерение трехфазного коэффициента мощности
Общий коэффициент мощности для трехфазной цепи определяется путем суммирования общей мощности в ваттах, деленной на общее значение ВА.
При использовании метода двух ваттметров сумма общей мощности (W1 + W2) делится на количество ВА. Однако, если нагрузка несбалансированная (фазные токи разные), это может привести к ошибке при расчете коэффициента мощности, поскольку при расчете используются только два измерения ВА.
При использовании метода трех ваттметров все три измерения ВА используются при расчете приведенного выше коэффициента мощности.
Гармоники
Гармоники относятся ко всем синусоидальным волнам, частота которых является целым кратным основной волны (обычно синусоидальный сигнал линии электропередачи 50 Гц или 60 Гц или от 0 до 2 кГц для вращающихся машин). Гармоники — это искажение формы волны нормального электрического тока, обычно передаваемое нелинейными нагрузками. В отличие от линейных нагрузок, где потребляемый ток пропорционален входному напряжению и соответствует форме волны, нелинейные нагрузки, такие как двигатели с регулируемой скоростью, потребляют ток короткими прерывистыми импульсами.
Гармоники необходимо контролировать, поскольку они могут вызывать ненормальный шум, вибрацию, нагрев или неправильную работу устройств и сокращать срок их службы. Для контроля гармоник существуют национальные и международные стандарты, такие как IEC61000-3. Поэтому инженерам необходимо обнаруживать гармоники и оценивать их влияние на компоненты, системы и подсистемы в приложении. Размер и разность фаз следует измерять не только для основной частоты, но и для каждой более высокочастотной составляющей. Высокоточные анализаторы мощности могут измерять гармоники выше 500-го порядка.
Для вращающихся машин основные амплитуды являются единственными компонентами, которые эффективно способствуют вращению оси. Все остальные гармонические компоненты приводят к потерям в виде тепла и вибрации.
Измерение гармоник
Используя режим измерения гармоник, можно измерить размер и разность фаз для каждой основной частоты, а также гармоники для каждой степени, включенной в ток, напряжение и мощность. В случае основной частоты (первичной составляющей) 50 Гц, например, третья составляющая составляет 150 Гц, пятая составляющая — 250 Гц и т. д., и возможно измерение до 500-й составляющей на частоте 2,5 кГц.
Рис. 25. Сумма нечетных гармонических составляющих в искаженном сигнале соотношение содержания и фазы в списке. Рис. 26. Гистограмма, показывающая энергию гармоник в зависимости от порядка. Эти измерения включают сложные уравнения, поэтому большинство компаний используют анализаторы мощности для автоматического получения результатов. Прецизионный высокочастотный анализатор мощности является важным инструментом для измерения как механической, так и электрической мощности. Его функции анализа и показания могут помочь улучшить работу и даже продлить срок службы двигателя.
23 факта, которые вы должны знать – Lambda Geeks
Треугольник власти | Треугольник тока напряжения питания
Треугольник мощности — это просто прямоугольный треугольник, сторона которого соответствует активной, реактивной и полной мощности. Компонент основания символизирует активную мощность, перпендикулярный компонент обозначает реактивную мощность, а гипотенуза символизирует полную мощность.
Что такое треугольник силы?
Определение треугольника власти | Определение треугольника мощности
Треугольник мощности — это графическое представление реальной или активной мощности, реактивной мощности и полной мощности в виде прямоугольного треугольника.
Уравнение силового треугольника | Треугольник мощности PQS
Расчет формулы треугольника мощности | Уравнение треугольника мощностей
В треугольнике мощностей активная мощность P, реактивная мощность Q и полная мощность S образуют прямоугольный треугольник.
Hypotenuse 2 = Основание 2 + Perpendicular 2
S 2 = P 2 + Q 2
ЗДЕСЬ. ВА).
Активная мощность (P) измеряется в ваттах (Вт).
Реактивная мощность (Q) измеряется в реактивных вольт-амперах (ВАр).
- Треугольник мощности — это графическое представление активной или активной мощности, реактивной мощности и полной мощности в виде прямоугольного треугольника.
- Активная или действительная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Измеряется в ваттах (Вт) или киловаттах (кВт) и представляется как P и среднее значение активной мощности P .
- Реактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. T также известен как мощность без ватт. Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка.
Реактивная мощность рассчитывается в реактивных киловольт-амперах (кВАр) и обозначается Q.
- Полная мощность в цепи, как поглощаемая, так и рассеиваемая, называется полной мощностью. Полная мощность вычисляется путем умножения среднеквадратичного значения напряжения на среднеквадратичное значение тока без учета фазового угла.
- Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, т. е. в цепи нет индуктивной или емкостной нагрузки. Но большинство цепей переменного тока состоят из последовательной или параллельной комбинации RLC. Из-за этого напряжение и ток становятся противофазными, и вводится комплексная величина.
- Мощность трехфазной системы = √3 x коэффициент мощности x напряжение x ток.
Силовой треугольник для цепи серии RLC | Цепи треугольника питания
Рассмотрим цепь RLC, соединенную последовательно, как указано выше.
Где резистор с сопротивлением R.
катушка индуктивности L.
конденсатор емкостью C.
Источник переменного напряжения V м sin⍵t применяется
В — среднеквадратичное значение приложенного напряжения, а I — среднеквадратичное значение полного тока в цепи. Катушка индуктивности и конденсатор дают Х L и X C оппозиций соответственно в цепи. Теперь может быть три случая:
Случай 1: X L > X C
Случай 2: X L < X C
Треугольник мощности получается из векторной диаграммы, если мы умножив каждый из векторов напряжения на I, мы получим три составляющие мощности.
Из векторного треугольника мы можем быстро получить треугольник мощности, умножив напряжения на I. Реальная мощность умножается на V R , что равно I 2 R. Реактивная мощность I умножается на (V C – V L ), что равно I 2 (X C – X L ).
Следовательно, комплексная мощность
S = P – jQ когда X L < X C
S = P + jQ, когда X L > X C
меньше емкостного сопротивления. Следовательно, реактивная мощность отрицательна, и угол ϕ также отрицателен. Для случая 2 значение индуктивного сопротивления больше, чем значение емкостного сопротивления, реактивная мощность равна +ve, а угол ϕ также равен +ve.
Треугольник активной реактивной полной мощности | Мощность вольт ампер треугольник
Треугольник активной и реактивной мощности .
Треугольник истинной силы .
Активная или истинная мощность относится ко всей мощности, рассеиваемой в электрической цепи. Измеряется в ваттах (Вт) или киловаттах (кВт) и представляется в виде P и среднего значения активной мощности P is,
P = VI = I 2 R
Треугольник реактивной мощности
Реактивная мощность или мнимая мощность — это мощность, которая не выполняет никакой реальной работы и вызывает нулевое рассеивание мощности. Он также известен как Вт без мощности . Это мощность, полученная от реактивных элементов, таких как индуктивная нагрузка и емкостная нагрузка. Реактивная мощность рассчитывается в киловольт-амперах реактивной (кВАр) и обозначается Q.
Реактивная мощность Q = VI реактивная = I 2 X.
Треугольник полной мощности
Полная мощность в цепи, как поглощаемой, так и рассеиваемой, называется полной мощностью.
Для чисто резистивной цепи реактивная мощность отсутствует. Итак, кажущаяся мощность равна активной или истинной мощности.
Силовой треугольник для цепи переменного тока | Треугольник электрической мощности
Цепи переменного тока могут иметь любую комбинацию R, L и C, и если мы хотим правильно рассчитать общую мощность, мы должны знать разность фаз между I и V. Форма волны тока а напряжение синусоидальное. Поскольку мощность = напряжение x ток, максимальная мощность достигается, когда обе формы волны совпадают. В этой ситуации формы волны называются «синфазными» друг с другом.
- В чисто резистивной схеме переменного тока I и V идеально совпадают друг с другом с точки зрения фазы. Следовательно, просто умножая их, мы можем получить мощность.
- Если в цепи имеется индуктивная или емкостная нагрузка, создается разность фаз. Даже если разница фаз незначительна, мощность переменного тока делится на две части: одну положительную и одну отрицательную. Отрицательная мощность не является математически отрицательной величиной; это просто означает, что в систему подается питание, но передачи энергии не происходит. Эта мощность известна как реактивная мощность. Положительная величина совершает некоторую реальную работу, поэтому ее классифицируют как реальную или активную мощность.
- Другая часть питания поступает в цепь от источника. Она известна как кажущаяся мощность. Полная мощность рассчитывается путем умножения среднеквадратичных значений тока и напряжения.
Треугольник силы по закону Ома | Треугольник силы Ома
Закон Ома всегда работает с цепями постоянного тока, но в случае переменного тока он работает только тогда, когда цепь является чисто резистивной, т.
Треугольник мощности для емкостной нагрузки
Емкостная нагрузка означает, что коэффициент мощности опережает ток по фазовому углу относительно напряжения.
Треугольник мощности для индуктивной нагрузки
Индуктивная нагрузка показывает, что коэффициент мощности отстает, поскольку I отстает от V на фазовый угол.
Треугольник комплексной мощности
Комплексная мощность есть не что иное, как представление мощности с использованием комплексных чисел. Действительная часть представляет собой активную мощность.
Предположим, что ток и напряжение в емкостной цепи равны I и V соответственно. Мы знаем, что для емкостной нагрузки I опережает V на фазовый угол. Примем этот угол за ϕ.
Допустим, напряжение на нагрузке V= ve jƟ и ток I = iej (Ɵ+ϕ) .
Мы знаем, мощность — это напряжение, умноженное на сопряженный ток.
Итак, комплексная мощность S = VI* = ve jƟ x ie -j(Ɵ+ϕ) = vie -jϕ
S = vi(cosϕ – jsinϕ) = vicosϕ – jvisinϕ = P – jQ [мы знаем активную мощность P = vicosϕ и реактивную мощность Q = visinϕ]
Для емкостной нагрузки I отстает от V на фазовый угол. Итак, напряжение на нагрузке V= ve jƟ и ток I = ie j(Ɵ-ϕ) .
So комплексная мощность
S = VI* = ve jƟ x ie-j (Ɵ-ϕ) = vie jϕ
S = vi(cosϕ + jsinϕ) = P vicosϕ + jvisinϕ
Трехфазный силовой треугольник
Переменный ток может быть однофазным или трехфазным.
Мощность трехфазной системы = √3 x коэффициент мощности x напряжение x ток.
Треугольник импеданса и треугольник мощности
Коэффициент мощности треугольника импеданса
В цепях постоянного тока только сопротивление отвечает за противодействие току. Но в цепях переменного тока величина, называемая реактивным сопротивлением, также противодействует току. Реактивное сопротивление может быть любой комбинацией индуктивности и емкости. Но и индуктивность, и емкость отличаются от сопротивления фазовым углом (отстающим или опережающим). Таким образом, мы не можем сложить их арифметически.
Коэффициент мощности [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности треугольника мощности
Коэффициент мощности в треугольнике мощности обозначается как отношение активной мощности к полной мощности, определяемое как косинус угла вектора.
Треугольник коррекции коэффициента мощности
Коррекция коэффициента мощности — это метод повышения эффективности электрической цепи за счет снижения реактивной мощности. Коррекция коэффициента мощности достигается за счет параллельно соединенных конденсаторов, которые противодействуют эффектам, вызванным индуктивными элементами, и уменьшают фазовый сдвиг.
Формула треугольника коэффициента мощности
Коэффициент мощности для емкостной или индуктивной нагрузки [Latex]= \frac{R}{Z}[/Latex]
Коэффициент мощности [Latex]= \frac{Real\; мощность {Очевидная \; power}[/Latex]
Треугольник энергии мощности
Электрическая энергия определяется как мощность системы, умноженная на общее время использования энергии.
Энергия E = P x T
Как нарисовать треугольник мощности?
Генератор треугольника мощностей
Треугольник мощностей строится с использованием активной мощности в качестве основания, реактивной мощности в качестве перпендикуляра и полной мощности в качестве гипотенузы.
Металлические треугольники на линиях электропередач
Мы часто видим несколько треугольных петель, свисающих с линий электропередач. Они используются для обеспечения устойчивости строп при сильном ветре. Эти треугольные ребра предотвращают подпрыгивание строп слишком близко друг к другу и гарантируют, что они не оторвутся от изоляторов. 9{2}} = 13\: \Omega[/Latex]
Коэффициент мощности цепи = R/Z = 12/13 = 0,92
Пример треугольника мощностей
Q. Нагрузка 20 кВт при коэффициент мощности 0,8 отстает. Найдите номинал конденсатора, чтобы он мог поднять значение коэффициента мощности до 0,95.

Здесь реальная мощность P = 20 кВт
Коэффициент мощности cosϕ 1 = 0,8
Мы знаем, что реактивная мощность должна быть уменьшена, чтобы получить увеличенный коэффициент мощности. Следовательно, фазовый угол также уменьшится. Предположим, что изначально фазовый угол был ϕ 1 , а после снижения реактивной мощности фазовый угол равен ϕ 2 . Итак, треугольник мощностей имеет вид-
Из диаграммы видно, что реактивная мощность уменьшилась до AB от переменного тока. Итак, нам нужно вычислить разницу AC и AB, и эта величина является требуемым номиналом конденсатора.
Здесь, OA = 20 кВт
Cos Вотство 1 = 0,8
Cos Воц 2 = 0,95
Мы знаем, Cos Вотство 1 = OA/OC
SO, OC = 20/0,8 = 25 KV.0007
AC = √ (OC 2 — OA 2 ) = 15 KVAR
COSЦ 2 = OA/OB
SO, OB = 20/0,95 = 21 KVA
AB = √ (OB 2 = 21 KVA
AB = √ (OB 2 2 = 21 KVA
AB = – OA 2 ) = 6,4 кВАр
Следовательно, BC = AC – AB = (15 – 6,4) = 8,6 квар
Часто задаваемые вопросы
Сколько типов степени степеней треугольника?
Треугольник мощности состоит из трех типов мощности
- – Истинная или активная мощность.
- – реактивная мощность.
- – полная мощность.
Что такое треугольник силы ? Объясните активную , реактивную и полную мощность на примере.
Треугольник мощности представляет собой треугольное представление отношения между активной мощностью, реактивной мощностью и полной мощностью.
Например, в любом электроприборе общая вырабатываемая мощность представляет собой части активной и реактивной мощности.
Что такое треугольник мощности цепи переменного тока?
Треугольник мощности цепи переменного тока может быть резистивным, емкостным или индуктивным, и треугольник состоит из трех видов мощностей, а полная мощность рассчитывается с помощью активной мощности и реактивной мощности.
Что такое треугольник мощности цепи RL?
Цепь RL имеет треугольник мощности с активной мощностью = I 2 R, реактивной мощностью = I 2 X L , а полная мощность = I 2 Z, где X L — индуктивное реактивное сопротивление, а Z — полное сопротивление цепи.
Какая связь между KVA, KW и KVAr?
КВА — это единица измерения полной мощности, а кВт и кВАр — это единицы активной мощности и реактивной мощности соответственно. Таким образом, из концепции треугольника мощностей можно сделать вывод, что кВА 2 = кВт 2 + кВАр.0515 2 .
Какое значение имеет коэффициент мощности?
Для индуктивных и емкостных нагрузок коэффициент мощности играет жизненно важную роль при расчете реактивной мощности. Реактивная мощность — это часть активной мощности, которая уменьшается, а коэффициент мощности — это отношение истинной мощности к полной мощности. Коэффициент мощности, равный единице, указывает на то, что цепь имеет полностью резистивный характер.
Сколько ватт составляет 6 кВА?
6 кВА = 6000 ВА
При единичном коэффициенте мощности 6 кВА = 1 x 6000 = 6000 Вт
Если коэффициент мощности другой, 6 кВА = 6 x (коэффициент мощности) Вт
Как преобразовать кВтч в кВАч?
кВтч = кВАч X коэффициент мощности
Следовательно, кВАч = кВтч/коэффициент мощности
Сколько ватт составляет 1 кВА?
Для чисто резистивной нагрузки реактивная мощность отсутствует.
. Если нагрузка емкостная или индуктивная, резистивная мощность не равна 0, поскольку коэффициент мощности представляет собой сопротивление/импеданс. Здесь 1 кВА = коэффициент мощности x 1 кВт
Почему электрические опоры имеют треугольную форму?
По следующим причинам электрические опоры имеют треугольную форму.
- Треугольники имеют большую площадь основания, что делает их очень жесткими. Эта жесткость помогает выдерживать боковые нагрузки.
- Треугольники имеют меньшую площадь, чем любой четырехугольник. Если бы форма была четырехугольной, то стоимость была бы больше. Треугольная форма снижает стоимость за счет исключения одной лишней стороны.
Какой коэффициент мощности у трансформатора?
Коэффициент мощности трансформатора зависит от характеристик нагрузки.
Если нагрузка чисто резистивная, коэффициент мощности равен единице или 1.





 Постепенно повышает опорный сигнал, пока не будет достигнуто равенство. Цифровые приборы достигают высокой точности.
Постепенно повышает опорный сигнал, пока не будет достигнуто равенство. Цифровые приборы достигают высокой точности.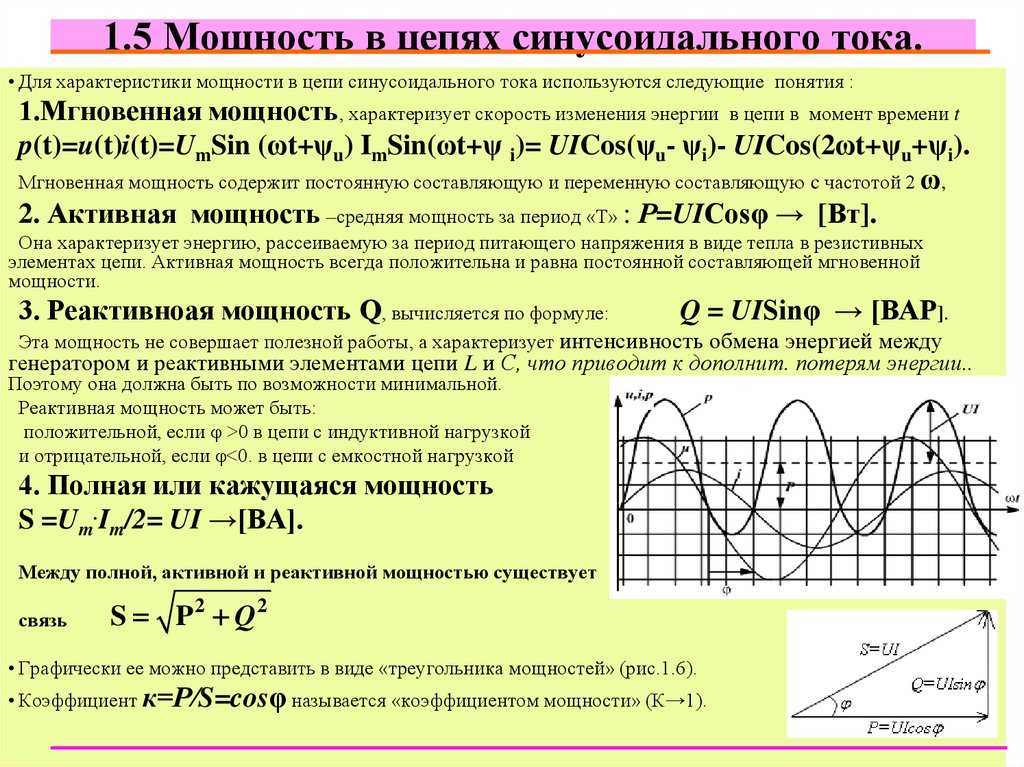
 Реактивная мощность рассчитывается в реактивных киловольт-амперах (кВАр) и обозначается Q.
Реактивная мощность рассчитывается в реактивных киловольт-амперах (кВАр) и обозначается Q. 

Добавить комментарий