Основные расчетные электротехнические формулы. Как найти f в электротехникеЭлектротехнические расчетные формулы. Электрическое сопротивление
Электротехнические расчетные формулы. Электрическое сопротивление
Понравился пост? Расскажи друзьям: elektrikov.net Некоторые формулы электротехники | Портал ЭлектриковЗакон Ома для участка цепи постоянного тока U=I*R, где U- напряжение на участке цепи, В, I- сила тока на этом участке, А, R — сопротивление участка цепи, Ом. Сопротивление проводника R=p*l/S где р — удельное сопротивление. Ом • м, l — длина проводника, м, S — площадь поперечного сечения проводника, м^2 Формула зависимости сопротивления проводника от температуры Rt=Rt0[1+a(t-t0)], где Rt и Rt0 — сопротивления проводника соответственно при температурах t и t0. С, а — температурный коэффициент сопротивления Ом/°С. Общее сопротивление цепи: при последовательном соединении сопротивлений R=R1+R2+R3+. .+Rn при параллельном соединении
Общая емкость конденсаторов: при последовательном соединении
при параллельном соединении С = С1 +С2 +С3+…+Сn. Мощность постоянного тока, Вт, Р=U*I Энергия электрической цепи, Дж, W =Pt. где Р — мощность, Вт, t — время, с. Количество теплоты, выделяющееся в проводнике, Дж, A=I^2Rt, где I — сила тока. А, R — сопротивление проводника, Ом, t — время прохождения тока, с. -акон Ома при переменном токе U =IZ. где Z — полное сопротивление, Ом.
где I — частота, Гц, w — число витков в катушке, В — индукция магнитного поля в стали магнитопровода, Т, S — площадь сечения магнитопровода, м^2. Подъемная сила электромагнита, Н, F=3978*B^2*S*10^2; где В — магнитная индукция. Т, S — площадь сечения электромагнита, м^2. Частота вращения магнитного поля электрической машины, об/мин, n=60f/p где р — число пар полюсов машины. Мощность однофазного переменного тока: активная, Вт, Р = U*Icosф, реактивная, вар, Q = UI sinф, полная, В-А,
Популярные запросы www.electricsite.net Основные расчетные электротехнические формулыЭлектрическое сопротивление материала определяется по формулам: Электрическое сопротивление, Ом, материала R = U/I, где U — напряжение, В; I — сила тока, А. Удельное электрическое сопротивление, Ом·м, ρ=Rs/l. S – сечение проводника, м² ; l – длина проводника, м. Под удельным электрическим сопротивлением материала понимают сопротивление проводника длиной 1 м и сечением 1 м² при 20°С. Величина, обратная удельному сопротивлению, называется проводимостью: v=1/ρ. Если вместо сечения проводника S задан его диаметр D, то сечение, м², находят по формуле S= πD²/4, где π =3,14. Сопротивление материала зависит от температуры. Если материал нагрет до температуры t°С, то его сопротивление, Ом, при этой температуре равно: Rt= R0[1 + α (t – t0)], где R0 – сопротивление при начальной температуре t0°С, Ом; α – температурный коэффициент. Далее приводятся значения α для различных материалов.
Сопротивление нескольких проводников зависит от способа их соединения. Например, при параллельном соединении сопротивление трех проводников определяется по формуле: Rоб=R1*R2*R3/(R1R2+R2R3+R3R1) При последовательном соединении: Rоб=R1+R2+R3. Постоянный токПостоянный ток применяют для питания устройств связи, транзисторных приборов, стартеров автомобилей, электрокар, а также, для зарядки аккумуляторов. В качестве источников постоянного тока используют гальванические элементы, солнечные батареи, термоэлектрогенераторы, генераторы постоянного тока. При параллельном соединении нескольких проводников с током с равными напряжениями: Iоб = I1+I2+…+In Uоб=U1=U2=…=Un При последовательном соединении: Iоб = Imin; – где Imin, ток наименьшего по мощности источника тока (генератора, аккумуляторной батареи). Uоб = U1+U2+…+Un Основные параметры цепей однофазного переменного токаОднофазный переменный ток промышленной частоты имеет 50 периодов колебаний в секунду, или 50 Гц. Его применяют для питания небольших вентиляторов, электробытовых приборов, электроинструмента, при электросварке и для питания большинства осветительных приборов. Частота переменного тока, Гц: f= 1/T = np/60, где п — частота вращения генератора, мин -1; р – число пар полюсов генератора. Мощность однофазного переменного тока: активная, Вт, Ра = IUcosφ; реактивная, вар, Q = IUsinφ; кажущаяся, В А, S = IU =√ (P 2α+Q 2) Если в цепь переменного однофазного тока включено только активное сопротивление (например, нагревательные элементы или электрические лампы), то значение силы тока и мощности в каждый момент времени определяют по закону Ома: I=U/R; Рa = IU = I²R=U²/R. Коэффициент мощности в цепи с индуктивной нагрузкой Cosφ= Рa/IU= Рa/S. Основные параметры цепей трехфазного переменного токаТрехфазный переменный ток используют для питания большинства промышленных электроприемников. Частота трехфазного переменного тока 50 Гц. В трехфазных системах обмотки генератора и электроприемника соединяют по схемам «звезда» или «треугольник». При соединении в звезду концы всех трех обмоток генератора (или электроприемника) объединяют в общую точку, называемую нулевой или нейтралью (рис. 5а). При соединении в треугольник начало первой обмотки соединяют с концом второй, начало второй обмотки — с концом третьей и начало третьей — с концом первой обмотки (рис. 5б). Если от генератора отходят только три провода, то такая система называется трехфазной трехпроводной; если от него отходит еще и четвертый нулевой провод, то систему называют трехфазной четырехпроводной. Трехфазные трехпроводные сети используют для питания трехфазных силовых потребителей, а четырехпроводные сети – для питания преимущественно осветительных и бытовых нагрузок. В трехфазных системах различают фазные и линейные токи и напряжения. При соединении фаз звездой линейный I и фазный Iφ токи равны: а напряжение U =√3Uφ При соединении треугольником I =√3Iφ а напряжение U = Uφ. Мощность переменного трехфазного тока: генератора:
где φ – угол сдвига фаз между фазным напряжением генератора и током в той же фазе приемника, который равен току в линии при соединении обмоток генератора звездой. приемника:
где φ – угол сдвига фаз между фазным напряжением приемника и током в той же фазе приемника, который равен току линейному только при соединении звездой. Подсчет количества теплоты, выделяемой при протекании электрического тока по проводнику. Количество теплоты, Дж, выделяемой электрическим током в проводнике, Q=I²Rt где t — время, с. При определении теплового действия электрического тока учитывают, что 1 кВт·ч выделяет 864 ккал (3617 кДж). Если у Вас остались вопросы – обращайтесь к нам, в авторизованный сервисный центр “Эл Ко-сервис” Мы всегда рады помочь Вам в решении возникших у Вас проблем. Инженерно-технический отдел авторизованного сервисного центра “Эл Ко-сервис” www.elko-service.ru 1.2. Некоторые формулы электротехники | Техническая библиотека lib.qrz.ru1.2. Некоторые формулы электротехники Закон Ома для участка цепи постоянного тока U=I*R, где U— напряжение на участке цепи, В, I— сила тока на этом участке, А, R — сопротивление участка цепи, Ом. Сопротивление проводника R=p*l/S где р — удельное сопротивление. Ом • м, l — длина проводника, м, S — площадь поперечного сечения проводника, м^2 Формула зависимости сопротивления проводника от температуры Rt=Rt0[1+a(t-t0)], где Rt и Rt0 — сопротивления проводника соответственно при температурах t и t0. С, а — температурный коэффициент сопротивления Ом/°С. Общее сопротивление цепи: при последовательном соединении сопротивлений R=R1+R2+R3+. .+Rn при параллельном соединении Общая емкость конденсаторов: при последовательном соединении при параллельном соединении С = С1 +С2 +С3+...+Сn. Мощность постоянного тока, Вт, Р=U*I Энергия электрической цепи, Дж, W =Pt. где Р — мощность, Вт, t — время, с. Количество теплоты, выделяющееся в проводнике, Дж, A=I^2Rt, где I — сила тока. А, R — сопротивление проводника, Ом, t — время прохождения тока, с. Закон Ома при переменном токе U =IZ. где Z — полное сопротивление, Ом. где I — частота, Гц, w — число витков в катушке, В — индукция магнитного поля в стали магнитопровода, Т, S — площадь сечения магнитопровода, м^2. Подъемная сила электромагнита, Н, F=3978*B^2*S*10^2; где В — магнитная индукция. Т, S — площадь сечения электромагнита, м^2. Частота вращения магнитного поля электрической машины, об/мин, n=60f/p
где р — число пар полюсов машины. Мощность однофазного переменного тока: активная, Вт, Р = U*Icosф, реактивная, вар, Q = UI sinф, полная, В-А, lib.qrz.ru Решение задач и курсовых по электротехнике Сайт Электротехника и электроника на «пять»Общая схема делителя тока представлена на рис.1. 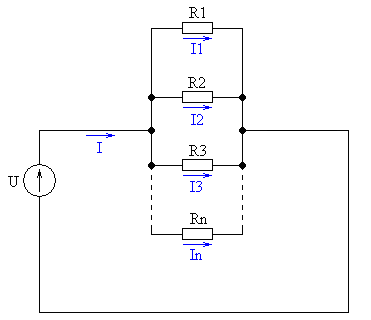 Рис.1 – Общая схема делителя тока Из схемы видно, что ток I разделяется на сопротивлениях на токи I1, I2, I3, … , In (n – количество резисторов). Нам известен ток I и сопротивления резисторов. Необходимо найти токи I1, I2, I3, … , In . Выведем общую формулу, позволяющую найти любой из этих токов. Для нахождения тока I заменим все резисторы эквивалентным (рис.2). 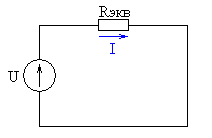 Рис.2 – Схема замещения резисторов Сопротивление эквивалентного резистора найдем из формулы параллельного соединения сопротивлений:
К сопротивлению Rэкв приложено напряжение U, значит, через этот резистор потечет ток I, который можно найти по закону Ома:
Значение тока I и сопротивление Rэкв нам известно, выразим U из формулы (2) и подставим Rэкв из выражения (1):
Выведем общую формулу, по которой можно найти ток в любой ветке. Найдем значение тока в i-й ветке по закону Ома:
Сопротивление резистора Ri (резистор в i-й ветке) нам известно, подставим в формулу (4) U из формулы (3):
То есть, по формуле
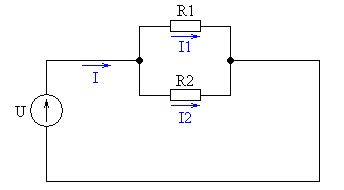
можно найти ток в любой ветке. В случае с двумя сопротивлениями (n=2) формула существенно упрощается. Схема делителя тока с двумя резисторами показана на рис.3.
Рис.3 – Схема делителя тока с двумя резисторами Формула (6) преобразуется:
По этой формуле найдем токи I1, I2:
Конечные формулы:
toe5.ru ПРОИЗВОДНАЯ В ЭЛЕКТРОТЕХНИКЕПроизводная – одно из фундаментальных понятий математики, это основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).Еще в древности был решен ряд задач дифференциального исчисления. Архимед, например, разработал способ проведения касательной, применимый для кривых. Само понятие производной возникло в XVII веке в связи с необходимостью решения физических, механических, математических задач, в первую очередь, следующих двух: определение скорости прямолинейного неравномерного движения и построение касательной к произвольной плоской кривой. Первой проблемой занимался великий Исаак Ньютон, второй проблемой – не менее великий Готфрид Лейбниц. Независимо друг от друга И. Ньютон и Г.Лейбниц разработали аппарат нахождения производной, которым мы и пользуемся в настоящее время. Благодаря дифференциальному исчислению, был решен целый ряд задач теоретической механики, физики и астрономии. Используя методы дифференциального исчисления, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVIII в. Основные понятия дифференциального исчисления долгое время не были должным образом обоснованы. Однако в начале XIX в. Французский математик О. Коши дал строгое построение дифференциального исчисления на основе понятия предела. В наши дни производная играет одну из самых главных ролей в науке и технике: с помощью дифференциального исчисления находят решение большинства задач в различных областях научного познания. В своей работе мы бы хотели подробнее рассмотреть приложение производной в технике: принцип ее работы, значение. В дальнейшем мы рассмотрим применение производной на примере нескольких задач, касающихся и нашей специальности «Электроэнергетика и электротехника». Очень важно знать, что производная показывает скорость изменения функции, или какого-либо процесса, величины как времени, так и по другим параметрам. Так как в практических приложениях обычно интересует не только сама функция, но и скорость ее изменения, то производная, будучи характеристикой скорости изменения, функции, имеет самые широкие практические применения в вопросах физики, химии, геометрии и т.д. Так, например: сила тока есть производная ,где Δq – положительный электрический заряд, переносимый через сечение проводника за время Δt. Примеры задач, в которых используют производную в различных дисциплинах специальности «Электроэнергетика и электротехника». Количество электричества, протекающее через проводник, начиная с момента времени t = 0, задается формулой Q = 3t2 – 3t + 4 Определить силу тока в конце 6-й секунды. Для нахождения силы тока используем известные формулы. Сила тока есть производная количества электричества по времени: следовательно, нужно найти производную функции Q = 3t2 – 3t + 4 и вычислить ее значение при t = 6 c. Имеем I = Q′ = 6t – 3, откуда при t = 6 получим I = 6∙6 – 3 = 33 (A). Задача о мгновенной величине тока. Обозначим через q = q(t) количество электричества, протекающее через поперечное сечение проводника за время t. Пусть Δt – некоторый промежуток времени, Δq = q(t + Δt) – q(t) количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока. Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt → 0. При изучении механического смысла производной пользуемся механическим истолкованием производной: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е. Ускорение движущегося тела представляет собой скорость изменения его скорости, т.е. Точка движется по окружности радиуса 4 м по закону S = 4,5t3, где S – путь в метрах, t – время в секундах. Найдем модуль ускорения точки в момент времени Т, когда ν=|ν|=6 м/с. По условию v = 6 м/с, значит, 13,5t2 = 6, t2 = 6/13,5,,t2 = 60/135, t2 = 4/9. Таким образом Касательное ускорение при t = T = 2/3 с; at = 27∙2/3 = 18 м/с2.
Нормальное ускорение Так как v = 6 м/с, p = r = 4 м, то an = 62/4 = 9 м/с2. Модуль полного ускорения точки: Умение дифференцировать позволяет исследовать различные функции. Используя задачи общетехнических и специальных дисциплин, мы формируем понимание глубокой общности в применении математического аппарата к широкому кругу разнообразных явлений природы. Мощность в переменном сопротивлении r2 определяется формулой P2 = IU – I2∙r1, где r1-const, Определить, при каком значении тока I получается наибольшее значение мощности P2. Значит, наибольшее значение мощности P2 при В заключении хотелось бы сказать о том, что энергетика, безусловно, является одним из приоритетных направлений развития общества и государства. При этом развитие цивилизации неразрывно связано с увеличением электропотребления, что, к сожалению, приводит к истощению природных ресурсов. Главнейшей задачей человечества становится предотвращение глобальной проблемы – экологической катастрофы. Ученые всех стран на теории и практике пытаются найти решение. В своих опытах они полагаются на такие дисциплины, как физика, экология, математика (в частности, применение производной). Задачи, рассмотренные в работе, применительно относятся к специальности: «Электроэнергетика и электротехника», так как позволяют узнать и применить производную в ее широком смысле. В наше время, в связи с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становится все более актуальным в решении как простых, так и сверхсложных задач. Таким образом, производная играет исключительную роль в электроэнергетике. Благодаря приложению производно в электроэнергетике, становится возможным решение множества задач, касающихся таких тем, как «Применение альтернативных источников энергии», «Измерение физических величин: мощности тока, индуктивности, емкостного напряжения», «Влияние электроэнергетики на окружающую среду».
Дата добавления: 2015-08-21; просмотров: 740 | Нарушение авторских прав Читайте в этой же книге: ВВЕДЕНИЕ | ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-го и 2-го ПОРЯДКА | ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ |mybiblioteka.su - 2015-2018 год. (0.058 сек.)mybiblioteka.su |
|
||||||||||||||||||
|
|
||||||||||||||||||
|




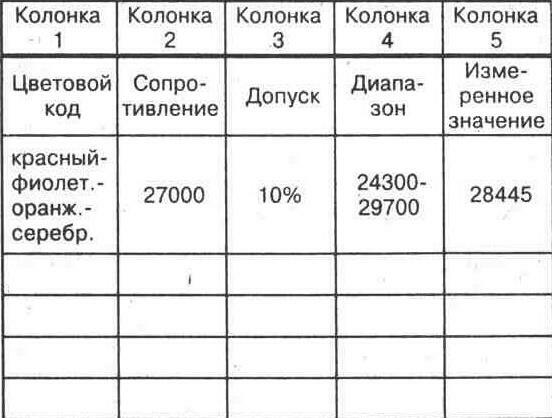
 В данной статье добавим ещё расчетные электротехнические формулы. Сопротивление в электротехнике имеет не маловажное значение.
В данной статье добавим ещё расчетные электротехнические формулы. Сопротивление в электротехнике имеет не маловажное значение.









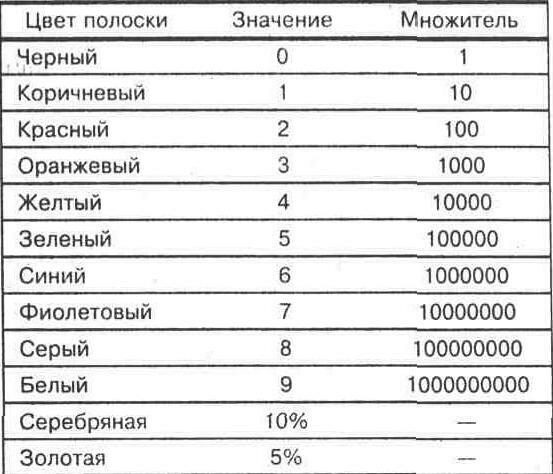
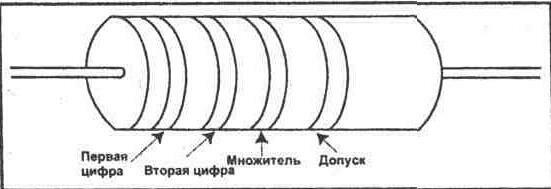


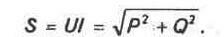

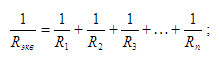 (1)
(1)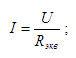 (2)
(2)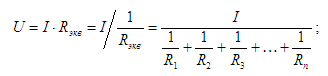 (3)
(3)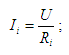 (4)
(4)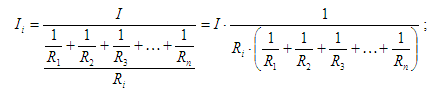 5)
5)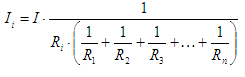 (6)
(6)
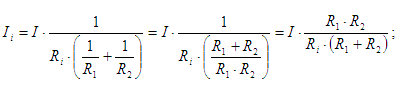 (6)
(6)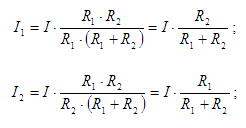 (7)
(7)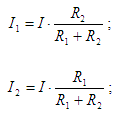 (8)
(8)









