J в электротехнике: что это такое, как их применять

ТОЭ Лекции — №15 Основные сведения о комплексных числах

Комплексным числом называется выражение вида:

где – c обозначение комплексного числа; a и b – соответственно действительная и
мнимая части комплексного числа; j=√(-1) – мнимая единица.

Величины a и b часто обозначают следующим образом: a = Re(c) , b = Im(c) . Символы
Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый.

Геометрически комплексное число изображается вектором на комплексной плоскости
(рис. 15.1). Горизонтальная и вертикальная оси, отмеченные соответственно знаками +1 и +j, называются
действительной (или вещественной) и мнимой. Действительная и мнимая составляющие комплексного числа
представляют собой проекции вектора на эти оси.

На рис.15.1

Модуль комплексного числа, равный длине вектора, а

— аргумент комплексного числа. Так как

— тригонометрическая форма комплексного числа. С помощью формулы Эйлера

последняя преобразуется в показательную форму:

Применяется еще и полярная форма

в самой простой форме задающая модуль и агрумент комплексного числа.

Свойства мнимой единицы (рис. 15.2):

Два комплексных числа c и c` называются сопряженными, если они имеют одинаковые
модули и равные по величине, но разные по знаку аргументы (рис. 15.3):

Изображающие их векторы симметричны относительно вещественной оси.

Действия над комплексными числами.

Сложение и вычитание производится над числами, записанными в алгебраической
форме:

т.е. складываются по отдельности вещественные и мнимые части слагаемых:

a=a1+a2; b=b1+b2

Операции сложения комплексных чисел соответствует сложение изображающих их
векторов.

Сумма сопряженных комплексных чисел равна удвоенному значению вещественной
части:

Умножение и деление комплексных чисел удобнее всего производить в показательной
форме. Модули при этом перемножаются или делятся, а аргументы складываются или вычитаются:

где

Что происходит с векторами при перемножении комплексных чисел?

На рис. 15.4 мы видим, что при умножении длина вектора возросла в с2 раз, а
аргумент увеличился на α2.Рассматривая комплексное число как вектор, мы приходим к следующему
выводу.

При умножении вектора на комплексное число аеjα , вектор растягивается в а раз и
поворачивается на угол α .

Произведение сопряженных комплексных чисел равно квадрату модуля комплексного
числа:

или

Иногда приходится производить умножение и деление комплексных чисел в
алгебраической форме. Перемножение выполняется по правилам умножения многочленов с учетом того, что j2 =
-1

При делении, чтобы получить результат, необходимо избавиться от мнимой единицы в
знаменателе. Этого можно достичь умножением числителя и знаменателя на сопряженный знаменатель:

где

Теория о комплексных числах — энергетик

Карл Фридрих Гаусс

    Первоначально идея о необходимости использования комплексных чисел возникла в результате формального решения кубических уравнений, при котором в формуле Кардано под знаком квадратного корня получалось отрицательное число.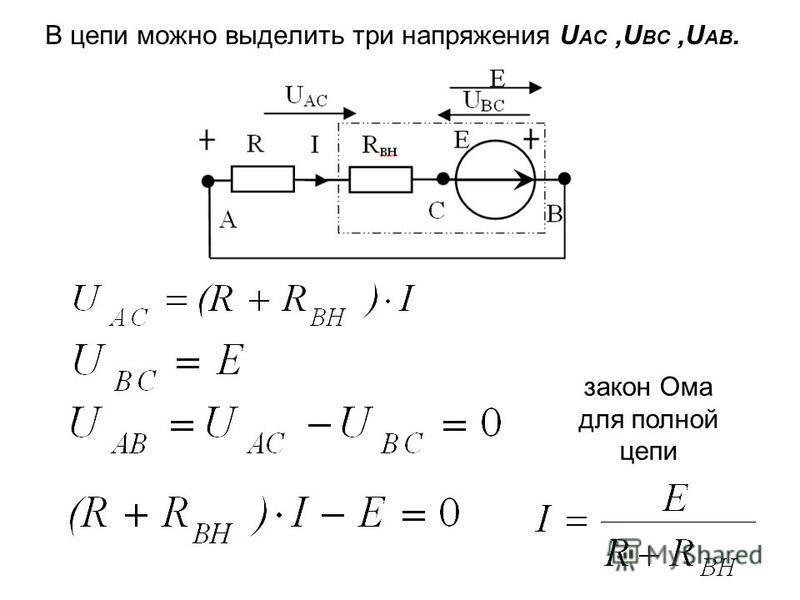 Сам термин «комплексное число» ввёл в науку Карл Гаусс в 1831 году.

   Итак, комплексные числа были введены в связи со следующей задачей, что действительных чисел недостаточно для того, чтобы решить любое квадратное уравнение. Напомним, что квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

     Заметим, что все квадратные уравнения можно условно разделить на три класса:
Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.
    К понятию комплексного числа привело стремление решить уравнение
x² +1 = 0 и извлечь корень из отрицательного числа.

Наряду с алгебраической формой  z = x + i y комплексного числа рассмотрим
еще две формы записи.

Тригонометрической формой комплексного числа , не равного нулю, называется запись  где  /z/— модуль комплексного числа, /φ/ — аргумент комплексного числа.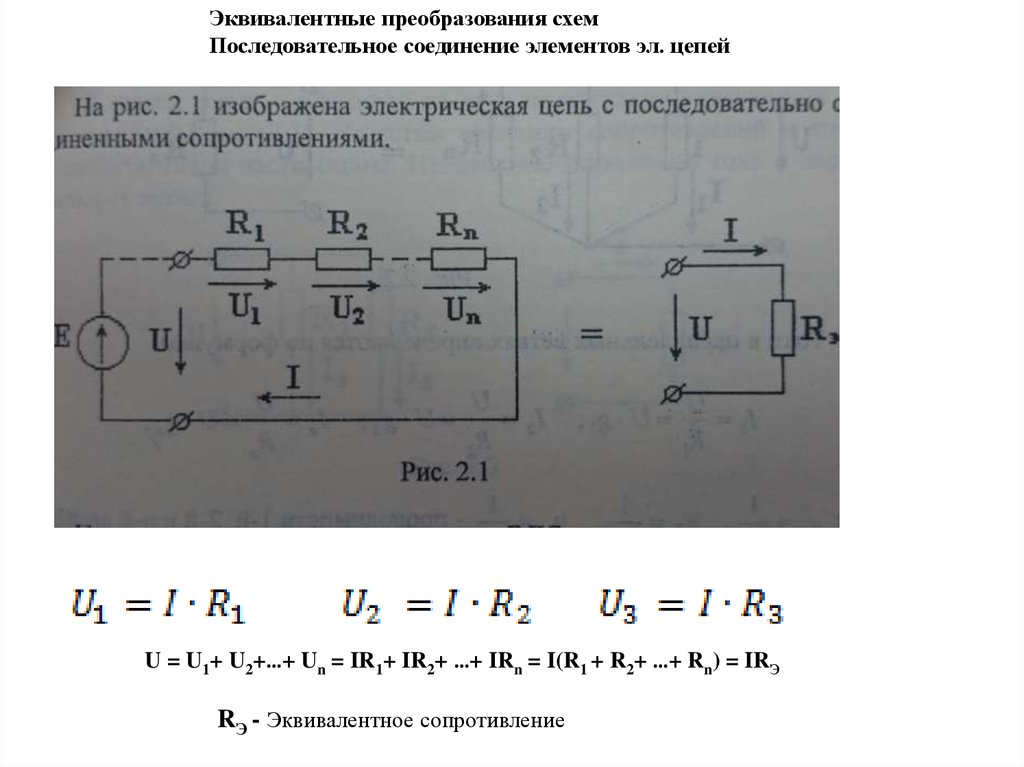  

И комплексное число  можно записать в так назы­ваемой показательной (или экспоненциальной) форме: z=re^iφ.

    Ввиду того, что традиционно символ i в электротехнике обозначает величину тока, мнимую единицу там обозначают буквой j, но принципиальной разницы нет как обозначать — j или i.  Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен – i = 1, то есть i² = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. 

     Сразу заметим, что арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Действительные числа (см. рис. ниже) – это и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой прямой обязательно соответствует некоторое действительное число.

  Сложение и вычитание комплексных чисел происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i² = –1). Число   = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z ·   = a² + b² позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:

 

 

 

   Напомним, чтобы всё было сразу понятно, если вмести нам вспомнить из школьной программы, то в математической литературе множества обозначаются с помощью больших букв латинского алфавита. Например:

A={0,5,6,−9},B={Δ,+,−5,0}.A={0,5,6,−9},B={Δ,+,−5,0}.

Нас интересует следующие обозначение:

• N– множество всех натуральных чисел;
• Z– множество целых чисел;
• Q– множество рациональных чисел;
• J– множество иррациональных чисел;
• R– множество действительных чисел;
• C– множество комплексных чисел.

Пример:  обозначенияг на графике см. Рис.(обозначение буквой R множество действительных чисел).

  Теперь пора вернутся как говорится «к нашим баранам», т.е. к комплексным числам, на графике обозначают, как уже отмечалось выше буквой C, ниже примеры графиков:

Понимание и отображение оператора J

You are here: Home / New Articles / Понимание и отображение оператора J

22 ноября 2017 г. Автор: David Herres 1 комментарий

Плюс, умноженный на плюс, есть плюс. Плюс умноженный на минус — это минус. Минус умноженный на плюс — это минус. Минус на минус — это плюс.

Поскольку ни одна из этих операций не приводит к отрицательному результату, мы должны признать суровую реальность того, что квадратный корень из отрицательного числа не существует. И все же √-1 появляется как промежуточный шаг во многих математических вычислениях, особенно в электротехнике. Признавая этот факт, числа, кратные √-1, стали называть «мнимыми числами».

Ворота в царство мнимых чисел — это строчные буквы j , которые широко используются в электронике. Можно сделать вывод, что i в нижнем регистре имело бы больше смысла, но j используется только во избежание путаницы, потому что i традиционно представляет ток. (Первоначально он обозначал интенсивность.) Соответствующая терминология — оператор j .

В электронике оператор j означает вращение вектора против часовой стрелки. Вектор — это нескалярное графическое представление комплексного числа, которое состоит из действительного числа и мнимого числа. Действительное число изображается длиной линии, представляющей вектор, а мнимое число изображается углом этой линии по отношению к осям X и Y.

В электронике все это проявляется, когда цепь переменного тока содержит нагрузку, полностью или частично емкостную или индуктивную. Частота не изменяется, но фаза тока, проходящего через нагрузку (а значит, и по всей цепи, в том числе и внутри обмоток генератора), смещается относительно приложенного напряжения.

Существует много непонимания того, как обращаться с мнимыми числами в электронике. Возьмите этот вопрос, недавно опубликованный на Reddit, например: На уроке физики, который я посещал в прошлом семестре, мы узнали о цепях RLC, и мой учитель как бы отмахнулся от мнимой части напряжения, сказав: «Нам важна только действительная часть». Так ли это на самом деле или есть просто более глубокая кроличья нора, в которую он не хотел лезть для целей нашего класса?……….. для (схемы) Q у нас есть действительная и мнимая части. Так что же означает воображаемая часть на самом деле? Если бы мы попытались увидеть это на осциллографе, смогли бы мы? Можем ли мы иметь какое-то устройство, которое измеряло бы заряд или напряжение в комплексной плоскости? Или все это не имеет значения, потому что воображаемая часть — это просто артефакт математики, не имеющий никакого реального значения?

Так что, возможно, краткий обзор параметра J в электротехнике не будет напрасным. В уравнении, описывающем поведение схемы, мнимая часть, обозначаемая оператором J, плюс действительная часть описывают фазовые соотношения между напряжением и током, а также форму волны, которая будет отображаться на осциллографе. Чтобы увидеть соотношение фаз на осциллографе, вам нужно будет отобразить интересующее напряжение и ток. Отставание и опережение между ними составляет фазовое соотношение.

Вектор импеданса отображается в первом квадранте полярной системы координат.

Мнимые члены возникают из-за того, что сопротивление переменному току представлено комплексной векторной величиной. Он отображается в полярной системе координат, где первый и второй квадранты соответствуют соответственно
пассивной индуктивности и пассивной емкости. Вектор импеданса состоит из действительной части, сопротивления (R), и мнимой части, реактивного сопротивления (X).

Как комплексный импеданс связан с Q и D.

Две формы реактивного сопротивления являются индуктивными (X _L ) и емкостной (X _C ). Коэффициент качества (Q) и коэффициент рассеяния (D) также имеют сопротивление и реактивное сопротивление в своих определениях. Эти параметры служат мерами чистоты реактивности. Чем больше Q или меньше D, тем лучше качество. Q определяется как отношение энергии, запасенной в компоненте, к энергии, рассеиваемой этим компонентом. D является обратным значением Q. D также равно «тангенсу δ», где δ – угол диэлектрических потерь (δ – угол, дополнительный к θ, фазовому углу). И D, и Q безразмерны.

Нельзя предполагать, что мгновенные значения напряжения и тока в точке цепи переменного тока совпадают по фазе. Таким образом, они должны быть выражены как действительная часть вектора и комплексной синусоиды e ^jωt ,

V и I комплексные амплитуды или вектора. Векторы также могут быть записаны как величины и фазовые углы. Конечно, фазовый угол вступает в игру при вычислении мощности. Мгновенная мощность в элементе схемы просто равна p(t) = v(t)i(t). Произведение двух косинусов дает постоянную (постоянную) составляющую и изменяющуюся во времени составляющую на удвоенной частоте. Усредненный по времени поток мощности получается путем интегрирования мгновенной мощности за один цикл, который сохраняет постоянную составляющую, в то время как 2wt составляющая усредняет до нуля: средний реальный поток мощности представляет собой действительную часть комплексной мощности, P _сред. = Re{Pc} = Re{½VI*}.

Фазовый угол и мгновенные напряжения и токи в реальных цепях переменного тока на самом деле более сложны, чем то, что выражают эти уравнения, потому что есть прямые и обратные компоненты, проходящие через реальные цепи переменного тока. Они могут быть определены количественно, но значительно усложняют анализ.

Возвращаясь к импедансам индуктора и конденсатора, напомним, что эти величины можно записать в полярной форме:

Следует отметить, что в отношении этих соотношений следует отметить, что действительная часть Z для обоих компонентов зависит от частоты. Мнимые части (e ^jπ/2 и e ^-π/2 ) постоянны. Это показывает, что в катушке индуктивности напряжение опережает ток на π/2, а в конденсаторе напряжение отстает от тока
на π/2. И это соотношение не меняется с частотой.

На снимке экрана анализатора импеданса Keysight E4990A показана частотная зависимость конденсатора емкостью 0,1 мкФ при изменении частоты от 20 Гц до 120 МГц. Вверху справа: график условного импеданса конденсатора и его фазового сдвига. Отметим также, что конденсатор перестает вести себя как конденсатор на высокой частоте. Фазовый сдвиг остается постоянным до тех пор, пока устройство не достигнет этой точки. Реальные устройства также ведут себя по-разному в зависимости от таких факторов, как уровень постоянного тока, который они видят. Внизу справа показана зависимость уровня постоянного тока, уровень постоянного тока изменяется от 0 до 10 В, частота = 1 кГц.

Интересно, что некоторые современные измерители LCR могут напрямую отображать эту зависимость. В качестве примера можно привести анализатор импеданса Keysight Technologies E4990A.

 

Рубрики: Часто задаваемые вопросы, Рекомендуемые, Измерители и тестеры, Новые статьи, Тестовое оборудование С тегами: keyighttechnologies

j Оператор и его значение

17 мая 2020 г. от admin

Что такое оператор j?

j Оператор — это математический оператор, который при умножении на любой вектор поворачивает этот вектор на 90 градусов против часовой стрелки. Подобно тому, как символы x, +, – и т. д. используются с числами для указания определенных операций, которые необходимо выполнить над этими числами, оператор j используется для обозначения поворота вектора против часовой стрелки на 90°.

Оператору j присвоено значение √(-1). Таким образом, это мнимое число. Двойная операция j над вектором поворачивает его против часовой стрелки на 180°. Таким образом, направление вектора меняется на противоположное, когда над вектором выполняется двойная операция j. Следовательно, мы можем написать

Объяснение оператора j:

Когда оператор j работает с вектором E , мы получаем новый вектор j E . Этот новый вектор j E смещен относительно исходного вектора E на 90° против часовой стрелки. Можно отметить, что величина вектора остается неизменной, когда вектор управляется j. Это показано на рисунке ниже.

Если «j» применяется к вектору j E , новый вектор j ₂ E будет равен 180° друг от друга в направлении против часовой стрелки. Это означает, что новый вектор j ₂ E противоположен исходному вектору E . Следовательно, мы можем сказать, что j ² E = – E . Для лучшего понимания вы можете обратиться к рисунку ниже.

Аналогично, когда j ² E оперируется с j, полученный таким образом новый вектор (j ³ E ) будет на 270° впереди E. Обратите внимание, что этот новый вектор противоположен вектору jE. Следовательно, мы можем сказать, j ³ E = jE. Точно так же j ⁴ E = E.

Из приведенного выше обсуждения мы можем перечислить некоторые важные свойства оператора j. Они следующие:

• j ² = -1
• j ³ = (j ² ) x j = -j
• j ⁴ = (j ² ) ² = 1
• (1/j) = -j

Значение:

В электротехнике оператор j имеет большое значение и применение. Вы часто будете сталкиваться с этим оператором в электрической машине, энергосистеме, сети переменного тока и т. д.

Как мы знаем, полное сопротивление цепи является комплексной величиной, т.е. имеет действительную часть и мнимую часть. Действительная часть означает резистивную часть, тогда как мнимая часть обозначает реактивную часть импеданса. Поскольку ток через реактивное сопротивление либо отстает от напряжения, либо опережает его на 90°, поэтому это реактивное сопротивление представляется с помощью оператора j.