Основные законы и формулы, описывающие цепи трёхфазного переменного тока. Формула тока в трехфазной цепи переменного тока3.2. Методика расчета трехфазных электрических цепей переменного тока3.2.1. Методика расчета трехфазных электрических цепей переменного тока при соединении потребителей звездойВ цепи, изображенной на схеме (рис. 3.1), потребители трехфазного тока соединены звездой. Известно линейное напряжение и сопротивления фаз: , ,,,,. Определить полные сопротивления фаз, фазные токи и ток в нейтральном проводе, активную, реактивную и полную мощности каждой фазы и всей цепи. Дано: , ,,,,,. Определить: Рис. 3.1 Графоаналитический метод расчета (расчет с применением векторных диаграмм)
Так как есть нейтральный провод, то
; ; -в фазе А напряжение отстает от тока на 60°. ; ; - в фазе В напряжение опережает ток на 60° ; -в фазе С напряжение отстает от тока на 90°, т. к. в цепь включен конденсатор.
; ; .
На векторной диаграмме под углом 120° друг относительно друга строятся векторы фазных напряжений одинаковой длины. Векторы фазных токов строятся в масштабе под вычисленными углами φ по отношению к фазным напряжениям. В фазе А нагрузка носит емкостный характер, значит, ток опережает напряжениена угол. В фазе В нагрузка носит индуктивный характер, следовательно, ток отстает от напряжениянa угол . В фазе С нагрузка емкостная, следовательно, ток опережает напряжениена угол. - масштаб.
Ток в нейтральном проводе равен геометрической (векторной) сумме фазных токов: Рис. 3.2
Измерив длину вектора , находим ток
Символический метод расчета Строгий аналитический расчет трехфазных цепей производится символическим методом, т. е. в комплексной форме.
Переведем комплексные сопротивления фаз из алгебраической формы в показательную:
где - полное сопротивление фазыА; - угол сдвига фаз между током и напряжением в фазе А. Аналогично определяем:
где ,.
где ,.
модуль , аргумент,
модуль , аргумент,
модуль , аргумент. Находим алгебраическую форму записи комплексов фазных токов:
модуль , аргумент.
где где где тогда где 3.2.2. Методика расчета трехфазных электрических цепей переменного тока при соединении треугольникомВ цепи, изображенной на схеме (рис. 3.3), потребители соединены треугольником. Известно линейное напряжение и сопротивления фаз.Определить фазные, линейные токи, мощности активные, реактивные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи. Дано: ,. Определить: ,,,,,, При соединении трехфазной цепи треугольником расчет будем вести Рис. 3.3 символическим метолом.
, то есть . Комплексы данных напряжений запишем из условия, что вектор совмещен с действительной осью комплексной плоскости
где
где
где
модуль ,;
модуль ,;
модуль ,.
модуль , аргумент;
модуль , аргумент;
модуль , аргумент.
, где , где , где где
Векторы фазных токов строятся под углами к действительной оси. К концам векторов пристраиваются отрицательные фазные токи согласно уравнениям: ; ; . Замыкающие векторные треугольники векторов представляют в выбранном масштабе линейные токи. Выбираем масштаб:
Рис. 3.4
Результаты расчета токов
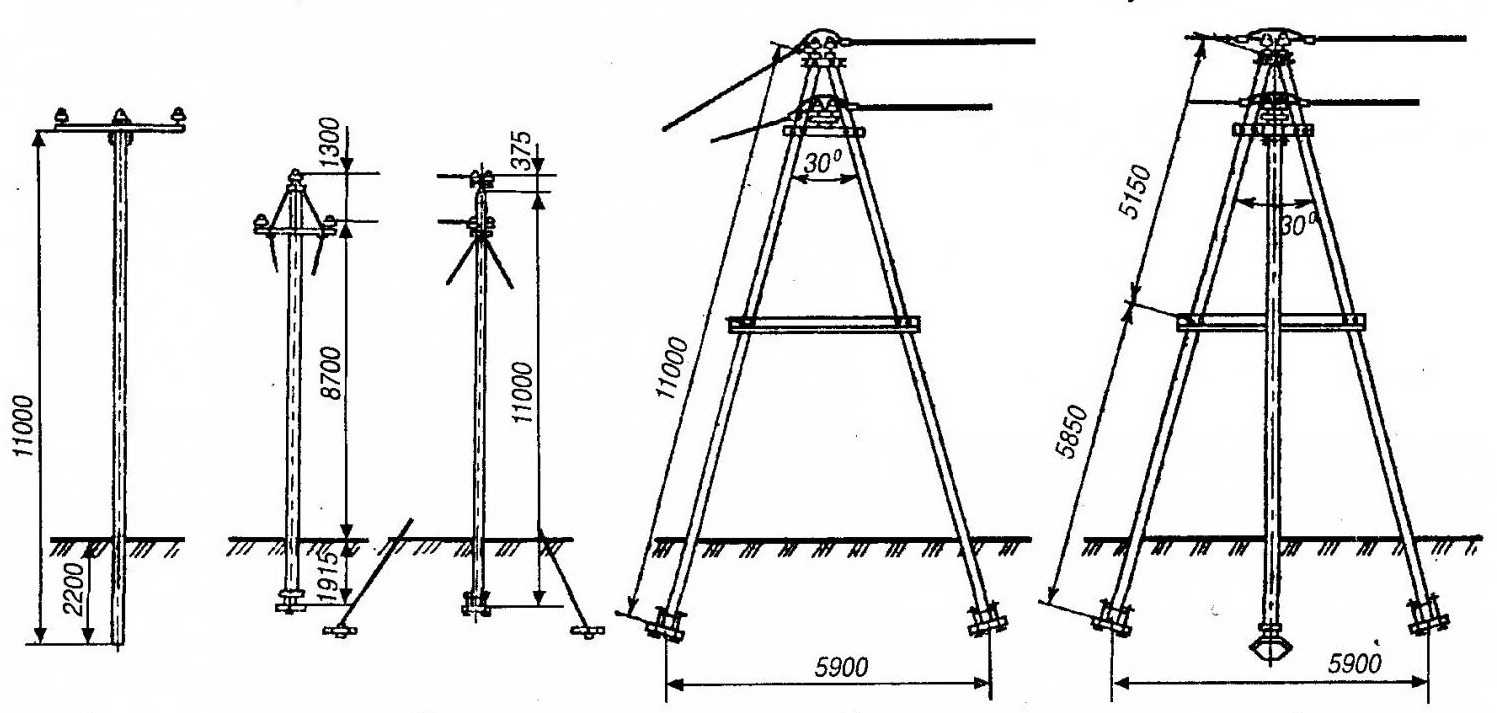
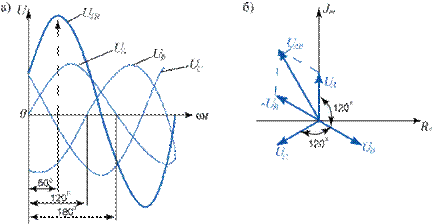
studfiles.net Основные законы и формулы, описывающие цепи трёхфазного переменного токаПриведём важнейшие законы из теории общей электротехники, касающиеся принципов работы электрооборудования на трёхфазном переменном токе. Синусоидальные токи и напряжения можно представлять как в виде мгновенных величин, так и в виде действующих. Мгновенные токи и напряжения описывают изменение физической величины в каждый момент времени и обозначаются малыми буквами i, u. Синусоидальный ток зависит от времени t по формуле: i(t) = imaxsin(ωt + φi), где imax – амплитуда синусоиды тока; ω – угловая частота; φi – начальная фаза. Угловая частота определяется по формуле: ω = 2π f, где f – частота переменного тока. Если принять f = 50 Гц, то ω = 314 рад/с. Аналогично определяется мгновенное напряжение: u(t) = umaxsin(ωt + φu), Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым проходит один и тот же ток, пропорциональны квадрату тока. Поэтому о величине тока можно судить по его среднеквадратичному значению за период, то есть по действующему значению. В этом случае применяют большую букву I. Действующее значение синусоидального тока численно равно такому постоянному току, который за период выделяет такое же количество тепла, что и синусоидальный ток. Аналогично вводится понятие действующего напряжения U. Действующее значение в Для удобства математического обращения с синусоидальными величинами токов и напряжений, их представляют в виде вращающихся векторов на комплексной плоскости. Так, например, симметричная трёхфазная система токов может быть представлена графически в виде тройки векторов, имеющих одинаковые длины и рассоложенных под углами 120° друг относительно друга – рис. 1.2.
Рис. 1.2. Изображение симметричной трёхфазной системы токов в виде векторов на плоскости
Такое представление позволяет графически складывать и вычитать токи и напряжения, анализировать сдвиг фаз между ними. Для трёхфазной системы напряжений вводятся понятия фазного и линейного напряжения. Фазное напряжение Uф – это разность потенциалов между фазой и «землёй» (то есть точкой нулевого потенциала). Линейное напряжение Uл – это разность потенциалов между двумя фазами. На рис. 1.3 показано графическое отображение фазных и линейных напряжений. Пользуясь тригонометрией, несложно доказать, что линейное напряжение в
Рис. 1.3. К понятию фазного и линейного напряжения
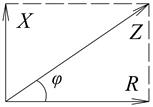
Закон Ома связывает напряжение U, ток I и полное сопротивление цепи Z: U = I ∙ Z. Полное сопротивление цепи состоит из активной R и реактивной Х составляющих: Z = Геометрически данное выражение можно представить в виде треугольника сопротивлений на рис. 1.4. Угол φ между активной и полной составляющей определяет разность фаз между синусоидами тока и напряжения. Косинус этого угла называется коэффициентом мощности и имеет очень важное значение для экономичности работы сети. При φ = 0 сопротивление цепи имеет число активный характер, а ток и напряжение совпадают по фазе.
Рис. 1.4. Треугольник сопротивлений
Активное сопротивление определяется удельным сопротивлением проводника ρ, его длиной l и площадью поперечного сечения s по формуле: R = ρ∙ l / s. Реактивное сопротивление Х может быть индуктивным (положительным) и емкостным (отрицательным). Индуктивное сопротивление катушки с индуктивностью L зависит от угловой частоты тока ω прямо пропорционально: ХL = ω L. Если сопротивление цепи чисто индуктивное, то синусоида тока отстаёт от синусоиды напряжения по фазе на 90° (φ = + 90°). Емкостное сопротивление конденсатора с ёмкостью С зависит от угловой частоты тока ω обратно пропорционально: ХС = 1 / ω С. Если сопротивление цепи чисто емкостное, то синусоида тока опережает синусоиду напряжения по фазе на 90° (φ = – 90°). Суммарное реактивное сопротивление складывается из сопротивлений ХL и ХС с учётом их знаков: Х = ХL – ХС. Закон электромагнитной индукции Фарадея описывает возникновение ЭДС в рамке при изменении магнитного потока. Фактически данный закон описывает принцип действия простейшего генератора переменного тока. Закон гласит: если внутри рамки изменять магнитный поток Ф, то на концах рамки возникнет ЭДС индукции εi, прямо пропорциональная скорости изменения магнитного потока dФ/dt и числу витков рамки N: εi = – N dФ/dt, где знак минус описывается правилом Ленца: индукционный ток, возникающий при изменении внешнего магнитного потока, имеет такое направление, что его собственный магнитный поток компенсирует изменение внешнего магнитного потока, вызвавшего этот ток. Важное значение в электротехнике имеет закон, описывающий взаимодействие проводника с током и магнитного поля. При помещении проводника длиной l с током I в магнитное поле с индукцией В, на данный проводник действует сила Ампера: FА = В∙I∙l∙sinα, где α – угол между векторами тока и магнитной индукции. Направление силы Ампера определяется по правилу левой руки: линии магнитного поля входят в ладонь, четыре пальца указывают направление тока, отставленный большой палец указывает направление силы Ампера. Данный закон описывает принцип действия любого электродвигателя. Закон Джоуля-Ленца оговаривает тепловое действие тока. Если через проводник сопротивлением R в течение времени t пропускать ток I, то в данном проводнике будет выделяться теплота количеством: Q = I2∙R∙t. Квадратичный характер тепловых потерь вынуждает при одной и той же мощности снижать ток за счёт увеличения напряжения, что активно используется в современной энергетике.
Похожие статьи:poznayka.org 22. Как рассчитать фазный ток, если известны линейное напряжение и сопротивление нагрузки в схеме треугольник.Схема треугольник В этой схеме (рис. 10.2,) токи в фазах при несимметричной нагрузке различны но напряжения остаются неизменными (номинальные). Линейные токи определяют по закону Кирхгофа
Мощность трехфазной несимметричной цепи. Для измерения активной мощности трехфазной нагрузки в общем случае, когда нагрузка несимметрична, используют 3 ваттметра (рис. 10.3, а), и тогда полная мощность равна сумме показаний ваттметров. При симметричной нагрузке достаточно одного ваттметра, включенного в одну из фаз. Трехфазную цепь с тремя проводами, соединяющими генератор с потребителем, всегда можно рассматривать как две двухпроводные линии, имеющие один общий провод, например как линии АВ и СВ с общим проводом В (рис. 10.3, б), в котором ток . При этом по первой линии при напряженииидет ток, а по второй линии при напряженииидет ток.
Рис. 10.3 Мощность, передаваемая по первой линии , а мощность, передаваемая по второй линии, Полная мощность, передаваемая по трехпроводной линии, S = S1 + S2. Из сказанного вытекает возможность измерять мощность, передаваемую по трехпроводной линии трехфазной системы, двумя ваттметрами, каждый из которых определяет мощность, передаваемую по одной из двух двухпроводных линий. Такая схема включения ваттметров (схема Арона) изображена на рис. 10.3, б. При выводе не делалось никаких предположений о симметрии системы, следовательно, найденный метод измерения мощности двумя ваттметрами применим как в случае симметричной, так и в случае несимметричной трехфазной трехпроводной системы. При чисто активной нагрузке (=0) показания обоих ваттметров одинаковы. Полное значение передаваемой (активной) мощности равно алгебраической сумме показаний обоих ваттметров. На практике часто два ваттметра ставятся на общую ось. Показания такого сдвоенного ваттметра непосредственно равны всей (активной) мощности, передаваемой по трехпроводной линии. Если определить разность показаний ваттметров W2–W1=UЛIЛsin, то по ней можно определить реактивную мощность . На основании последних выражений легко вывести формулу, позволяющую определить угол по показаниям ваттметров:
23. Как определяется мощность в трёхфазных цепях?.Вычисление величины полной мощности. Расчет полной мощности электрической цепи требует знания ее активной и реактивной составляющих, соотношение которых в любой схеме описывается треугольником мощностей. Для вычисления активной (Р) и реактивной (Q) составляющих 3-х фазной цепи проводится суммирование их величин в каждой фазе по формулам: Р=РA+РB+РC=UAIAcosφA+UВIВcosφВ+UСIAСcosφС; Q=QA+QB+QC=UAIAsinφA+UВIВsinφВ+UСIAСsinφС. IA, IВ, IС, UA, UВ, UС – вектора токов и напряжений в фазах, Φ – угол сдвига фаз векторов тока относительно напряжения. Для симметричного режима работы схемы во всех фазах выполняется равенство мощностей. Поэтому общую величину мощности можно получить простым умножением фазной составляющей на количество фаз в системе: Р=3РФ=3UФ∙IФ∙cosφ; Q=3Q=3UФ∙IФ∙sinφ; S=3SФ=(Р2+Q2)=3UФIФ. Делаем замену фазных составляющих линейными по их соотношениям для схемы звезды: IЛ=IФ, UФ=UЛ/√3. В результате получаем: Р=3UФ∙IФ∙cosφ=(3UЛ∙IЛ/√3)∙cosφ=√3∙UЛ∙IЛ∙cosφ. Заменяем фазные составляющие линейными для схемы треугольника по их соотношениям: IФ=IЛ/√3, UФ=UЛ. Итог вычисления: Р=3UФ∙IФ∙cosφ=(3UЛ∙IЛ/√3)∙cosφ=√3∙UЛ∙IЛ∙cosφ. Таким образом, получилось, что зависимость от вариантов соединения элементов цепи схемой γ либо Δ в 3-х фазной симметричной системе значения мощностей отсутствует. Они вычисляются по одним и тем же формулам: Р=√3∙U∙I∙cosφ [Вт]; Q=√3∙U∙I∙sinφ [вар]; S=√(Р2+Q2) [ВА]. Для данных выражений сложилось правило: подставлять линейные значения векторов U и I без указания их линейных индексов. Способы измерений мощности В энергетике существует постоянная необходимость измерения электрических величин. Активная составляющая полной мощности замеряется ваттметром, а реактивная – варметром. Ваттметр работает по алгоритму, описанному формулой: W=UW∙IW∙cos(UW^IW)=Re│UW∙IW*│. UW, IW – те вектора, которые подвели к клеммам прибору для замера активной составляющей. Практика электрических измерений предлагает несколько вариантов подключения к электросети ваттметров. Они выбираются в зависимости от схемы выполненный коммутации нагрузок и ее характеристик. В симметричной 3-х фазной системе достаточно включить один ваттметр в любую фазу для постоянного замера активной мощности с последующим утроением полученного результата по алгоритму Р=3W=3UФ∙IФ∙cosφ. Однако, этот простой способ только ориентировочно оценивает замеряемые величины, имеет большие погрешности. Поэтому, он малоприемлем для выполнения замеров, требующих высокой точности и в решении коммерческих задач. Более точные замеры активной составляющей для звезды с нейтральным проводом обеспечивает использование в измерении трех ваттметров. studfiles.net Расчет трехфазных цепей (Лекция №17)Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах. Расчет симметричных режимов работы трехфазных систем Многофазный приемник и вообще многофазная цепь называются симметричными,
если в них комплексные сопротивления соответствующих фаз одинаковы, т.е.
если Если к симметричной трехфазной цепи приложена симметричная трехфазная система
напряжений генератора, то в ней будет иметь место симметричная система токов.
Такой режим работы трехфазной цепи называется симметричным. В этом режиме
токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг
по отношению к другу на угол Так для симметричного режима работы цепи на рис. 2,а при известных линейном
напряжении и сопротивлениях фаз где Тогда на основании вышесказанного
Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает: При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов: Все треугольники заменяются эквивалентными звездами. Поскольку треугольники
симметричны, то в соответствии с формулами преобразования «треугольник-звезда»
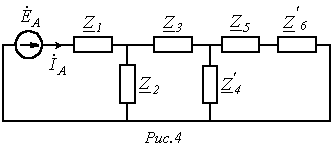
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах. Пусть, например, при заданном фазном напряжении В соответствии с указанной методикой выделим расчетную фазу А, которая представлена
на рис. 4. Здесь Тогда для тока и соответственно Расчет несимметричных режимов работы трехфазных систем Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее. При заданных линейных напряжениях наиболее просто рассчитываются трехфазные
цепи при соединении в треугольник. Пусть в схеме на рис. 2,а По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи: Обычно на практике известны не комплексы линейных напряжений, а их модули.
В этом случае необходимо предварительное определение начальных фаз этих напряжений,
что можно осуществить, например, графически. Для этого, приняв
Тогда Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов: При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет. Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной
нагрузке Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением
смещения нейтральной точки (обычно принимается, что Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:
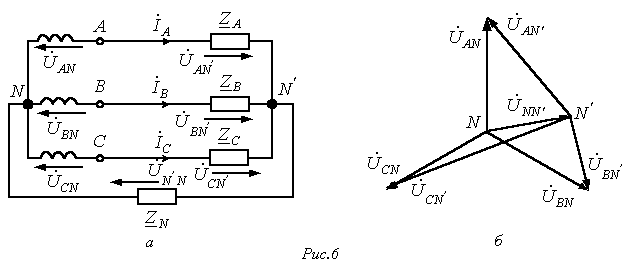
Тогда для искомых токов можно записать: Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
При наличии нейтрального провода с нулевым сопротивлением
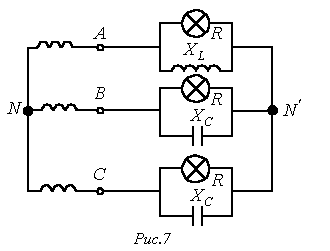
В качестве примера анализа несимметричного
режима работы цепи с использованием соотношения (1) определим, какая из ламп
в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если
Запишем выражения комплексных сопротивлений фаз нагрузки: Тогда для напряжения смещения нейтрали будем иметь Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается) Таким образом, наиболее ярко будет гореть лампочка в фазе С. В заключение отметим, что если при соединении в звезду задаются линейные напряжения
(что обычно имеет место на практике), то с учетом того, что сумма последних
равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например,
Литература
Контрольные вопросы и задачи
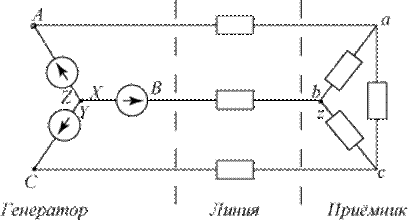
Определить ток в нейтральном проводе. Ответ: Определить ток в нейтральном проводе. Ответ: Определить фазные напряжения на нагрузке. Ответ: Определить фазные напряжения на нагрузке. Ответ: www.toehelp.ru Трёхфазные цепи переменного токаЭлементы трёхфазных цепей переменного тока. Генераторы, линии передачи электроэнергии, электродвигатели оказываются технически более совершенными, и в конечном итоге более выгодными экономически, если они построены на принципах трёхфазных цепей переменного тока. Создание в 1889г. выдающимся русским учёным Михаилом Осиповичем Доливо-Добровольским (1862 г – 1919 г) связанной трёхфазной цепи переменного тока явилось важным событием в истории электротехники. (Он же изобрёл и асинхронный двигатель АД). Трёхфазная электрическая цепь является упорядоченным электрическим соединителем трёх источников переменного напряжения (или тока), имеющих постоянную разность временных фаз, и трёх потребителей (или трёх групп потребителей) электроэнергии. Каждая ветвь трёхфазной цепи называется фазой. Упорядоченность трёхфазной цепи проявляется в том, что в фазах источником обеспечивается примерное равенство амплитуд напряжений, а также амплитуд токов. Это достигается конструкцией генераторов и выравниванием сопротивлений фаз потребителей. Для получения трёхфазного тока на электростанциях применяют специальные трёхфазные генераторы, имеющие три обмотки, сдвинутые относительно друг друга и поэтому дающие три ЭДС с фазовым сдвигом 1200 между собой. Наличие двух различных напряжений является одним из достоинств трёхфазного тока.
рис.8.2. Графики а) и векторная диаграмма б) фазных и одного линейного напряжения Каждая фаза имеет начало и конец. Начало фаз принято обозначать латинскими буквами A, B, C, а концы – буквами X, Y, Z (для генератора), малыми буквами a, b, c (начала), x, y, z (концы) – для потребителя Практически используются две схемы симметричных соединений трёх фаз: звезда (рис.8.3а), когда соединяются вместе концы всех обмоток X, Y, Z, и треугольник (рис.8.3б), когда соединяются начало одной обмотки с концом другой в последовательности A – Z, B – X, C – Y.
Фазы генератора: Начала и концы фаз обозначаются соответственно: A – X, B – Y, C – Z.
Фазы потребителя: Начала и концы фаз обозначаются соответственно: a – x, b – y, c – z.
рис.8.3.
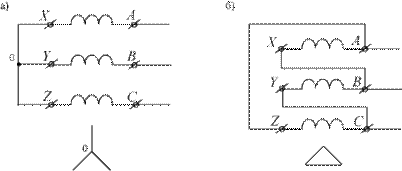
рис.8.4. Фазы трёхфазного генератора (источника) соединяются либо звездой (соединение точек X, Y, Z), либо треугольником (соединение A – Z, B – X, C – Y). Фазы трёхфазного потребителя обозначаются малыми буквами (x, y, z; a, b, c). Варианты схем соединений фаз источников и приёмников И П
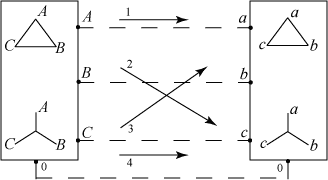
рис.8.5. 1 – «треугольник» - «треугольник» 2 – «треугольник» - «звезда» 3 – «звезда» - «треугольник» 4 – «звезда» - «звезда».
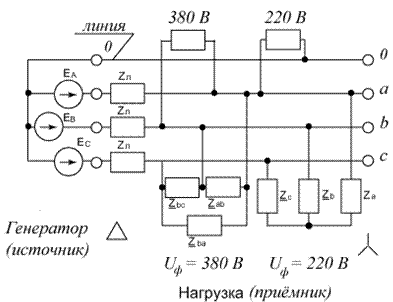
Трёхпроводная линия соединяет начала соответствующих фаз источника и приёмника ( A – a, B – b, C – c). Участки цепи A – a, B – b, C – c называются фазами линии. Возможны любые сочетания схем соединений у источника «И» и приёмника «П» (рис.8.5.). В цепях с соединением «звезда» - «звезда» используется также четвёртая линия, соединяющая нуль источника (соединение X, Y, Z) и нуль приёмника (соединение x, y, z). Эта соединительная нейтраль называется нейтральным (нулевым) проводом. В трёхфазной цепи возможно включение отдельных однофазных потребителей (или их сочетаний) на фазы линии и на одну фазу и нулевой провод (рис.8.6.).
рис.8.6. Провода, соединяющие фазы генератора и приёмника, называются – линейными, а токи в них линейными токами ( Фазными токами называются токи, протекающие по фазам, причём у источников их положительные направления принимаются от конца фазы к её началу ( Мгновенные значения токов генератора описываются уравнениями:
Похожие статьи:poznayka.org |
|
||||||||||||||||||
|
|
||||||||||||||||||
|




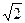 раз меньше амплитудного.
раз меньше амплитудного.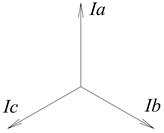
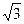 раз больше фазного. Так, например, для сетей жилых зданий линейное напряжение составляет 380 В, а фазное 380/корень3 ≈ 220 В.
раз больше фазного. Так, например, для сетей жилых зданий линейное напряжение составляет 380 В, а фазное 380/корень3 ≈ 220 В.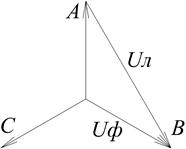
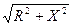 .
.
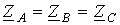 . В противном случае они являются
несимметричными. Равенство модулей указанных сопротивлений не является
достаточным условием симметрии цепи. Так, например трехфазный приемник на рис.
1,а является симметричным, а на рис. 1,б – нет даже при условии:
. В противном случае они являются
несимметричными. Равенство модулей указанных сопротивлений не является
достаточным условием симметрии цепи. Так, например трехфазный приемник на рис.
1,а является симметричным, а на рис. 1,б – нет даже при условии: 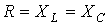 .
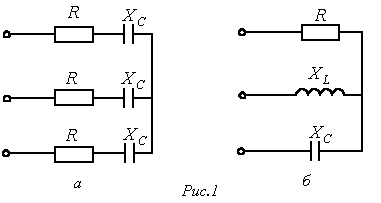
.
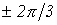 . Вследствие указанного расчет
таких цепей проводится для одной – базовой – фазы, в качестве которой
обычно принимают фазу А. При этом соответствующие величины в других фазах получают
формальным добавлением к аргументу переменной фазы А фазового сдвига
. Вследствие указанного расчет
таких цепей проводится для одной – базовой – фазы, в качестве которой
обычно принимают фазу А. При этом соответствующие величины в других фазах получают
формальным добавлением к аргументу переменной фазы А фазового сдвига 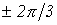 при сохранении неизменным ее модуля.
при сохранении неизменным ее модуля.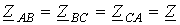 можно записать
можно записать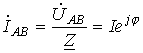 ,
,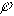 определяется характером нагрузки
определяется характером нагрузки 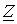 .
.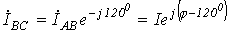 ;
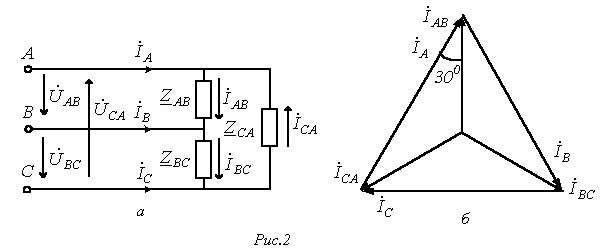
;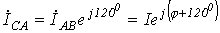 .
.
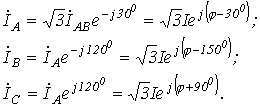
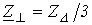 .
. 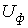 необходимо определить линейные
токи
необходимо определить линейные
токи 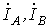 и
и 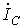 в схеме на рис. 3, все сопротивления
в которой известны.
в схеме на рис. 3, все сопротивления
в которой известны.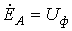 ,
, 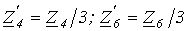 .
. 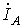 можно записать
можно записать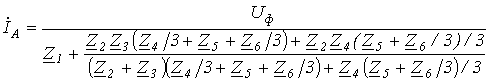 ,
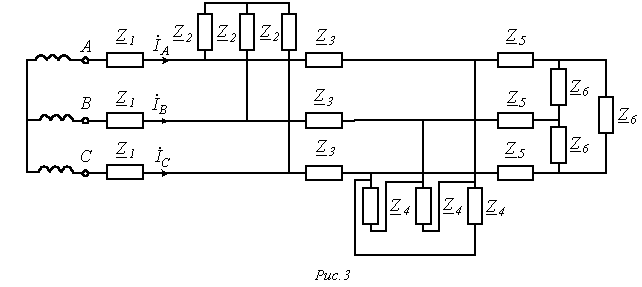
,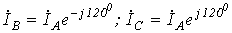 .
.
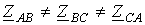 . Тогда при известных комплексах
линейных напряжений в соответствии с законом Ома
. Тогда при известных комплексах
линейных напряжений в соответствии с законом Ома 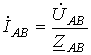 ;
; 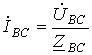 ;
; 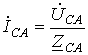 .
.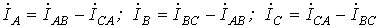 .
.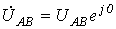 , по заданным модулям напряжений,
строим треугольник (см. рис.5), из которого (путем замера) определяем значения
углов a и b.
, по заданным модулям напряжений,
строим треугольник (см. рис.5), из которого (путем замера) определяем значения
углов a и b.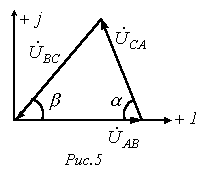
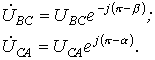
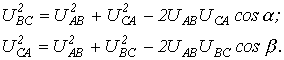
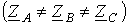 ей в общем случае будет соответствовать
векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки
источника и приемника занимают разные положения, т.е.
ей в общем случае будет соответствовать
векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки
источника и приемника занимают разные положения, т.е. 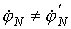 .
. 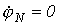 ) или просто напряжением смещения
нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке,
что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
) или просто напряжением смещения
нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке,
что наглядно иллюстрирует векторная диаграмма на рис. 6,б.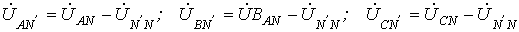 .
.
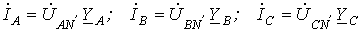 .
.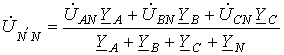 .
.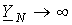 , и из (1)
, и из (1) 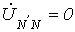 . В случае отсутствия нейтрального
провода
. В случае отсутствия нейтрального
провода 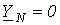 . При симметричной нагрузке
. При симметричной нагрузке 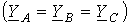 с учетом того, что
с учетом того, что 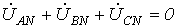 , из (1) вытекает
, из (1) вытекает 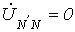 .
.
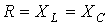 .
.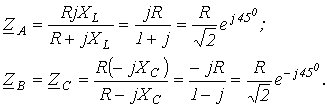
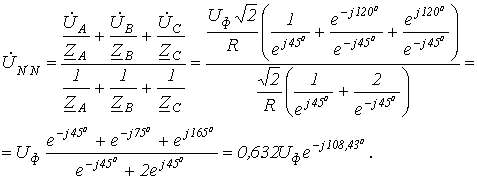
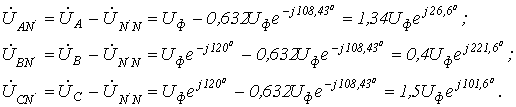
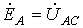 и
и  . Тогда, поскольку при этом
. Тогда, поскольку при этом 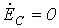 , соотношение (1) трансформируется
в формулу
, соотношение (1) трансформируется
в формулу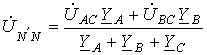 .
. ;
; 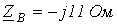 ;
; 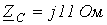 ;
; 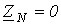 . Линейное напряжение равно 380
В.
. Линейное напряжение равно 380
В.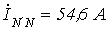 .
.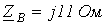 ;
; 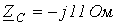 . Остальные параметры те же.
. Остальные параметры те же. 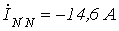 .
.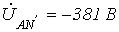 ;
; 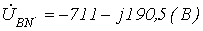 ;
; 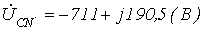 .
.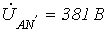 ;
; 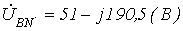 ;
; 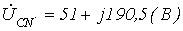 .
.
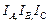 ). Напряжение этих токов условно принято указывать от генератора к приёмнику, также как направление ЭДС (
). Напряжение этих токов условно принято указывать от генератора к приёмнику, также как направление ЭДС ( 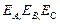 ) от концов фаз к их началам. Напряжения между началами и концами фаз генератора называются фазными и обозначаются
) от концов фаз к их началам. Напряжения между началами и концами фаз генератора называются фазными и обозначаются 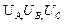 . Напряжения между началами фаз генератора называются линейными и обозначаются
. Напряжения между началами фаз генератора называются линейными и обозначаются 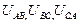 .
.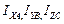 ), а у приёмников – в противоположном направлении (
), а у приёмников – в противоположном направлении ( 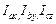 ).
).