Электротехника конденсатор: Конденсатор: устройство, принцип работы, применение

Калькулятор емкости последовательного соединения конденсаторов • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Калькулятор позволяет рассчитать емкость нескольких конденсаторов, соединенных последовательно.

Пример. Рассчитать эквивалентную емкость двух соединенных последовательно конденсаторов 10 мкФ и 5 мкФ.

Входные данные

C1 фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)

C2 микрофарад (мкФ)

Добавить конденсатор

Поделиться

Поделиться ссылкой на этот калькулятор, включая входные параметры

Twitter Facebook Google+ VK

Закрыть

Выходные данные

Эквивалентная емкость

C микрофарад (мкФ)

Введите значения емкости в поля C1 и C 2, добавьте при необходимости новые поля, выберите единицы емкости (одинаковые для всех полей ввода) в фарадах (Ф), миллифарадах (мФ), микрофарадах (мкФ), пикофарадах (пФ), нанофарадах (нФ) и нажмите на кнопку Рассчитать.

1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф. 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.

В соответствии со вторым правилом Кирхгофа, падения напряжения V₁, V₂ and V₃ на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V равна их сумме:

По определению емкости и с учетом того, что заряд Q группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость Ceq всех трех конденсаторов, соединенных последовательно, определяется как

или

Для группы из n соединенных последовательно конденсаторов эквивалентная емкость Ceq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:

или

Эта формула для Ceq и используется для расчетов в этом калькуляторе. Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:

Если конденсаторов только два, то их общая емкость определяется по формуле

или

Если имеется n соединенных последовательно конденсаторов с емкостью C, их эквивалентная емкость равна

Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов.

Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.

Конденсаторы на печатной плате

Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки. На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.

Выравнивающие резисторы уменьшают разброс напряжений на отдельных конденсаторах

Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах. Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.

Если несколько конденсаторов соединены параллельно, разность потенциалов V на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах Q₁, Q₂ and Q₃ тоже будут различными. Общий заряд определяется как

Конденсаторы, соединенные параллельно

По определению емкости, эквивалентная емкость группы конденсаторов равна

отсюда

или

Для группы n включенных параллельно конденсаторов

То есть, если несколько конденсаторов включены параллельно, их эквивалентная емкость определяется путем сложения емкостей всех конденсаторов в группе.

Возможно, вы заметили, что конденсаторы ведут себя противоположно резисторам: если резисторы соединены последовательно, их общее сопротивление всегда будет выше сопротивлений отдельных резисторов, а в случае конденсаторов всё происходит с точностью до наоборот.

Конденсаторы на печатной плате

Автор статьи: Анатолий Золотков

Практическая работа конденсаторы электротехника

Содержание

  1. Практическая работа №1 по Электротехнике и электронике методическая разработка
  2. Скачать:
  3. Предварительный просмотр:
  4. Практическая работа №1
  5. Практическая работа Конденсаторы.
  6. Просмотр содержимого документа «Практическая работа Конденсаторы.»
  7. Практическая работа №2 последовательное и параллельное соединение конденсаторов
  8. Практическая работа «Последовательное и параллельное соединение конденсаторов. Эквивалентные схемы»
  9. Просмотр содержимого документа «Практическая работа «Последовательное и параллельное соединение конденсаторов. Эквивалентные схемы»»

Практическая работа №1 по Электротехнике и электронике

методическая разработка

Практическая работа №1 Расчет смешанного соединения конденсаторов по дисциплине Электротехника и электроника

Скачать:

Вложение Размер
prakticheskaya_rabota_no1. docx 116.51 КБ

Предварительный просмотр:

Практическая работа №1

Тема: «Расчет смешанного соединения конденсаторов»

Цель: закрепить знания методов расчета электрической емкости и зарядов конденсаторов при их смешанном соединении.

В результате выполнения практической работы обучающийся должен

знать: основные законы параллельного и последовательного соединения конденсаторов;

уметь: производить расчет эквивалентной емкости и заряд конденсаторов.

Оборудование и инструменты: карандаш, линейка.

Краткие теоретические сведения

Электрический конденсатор —это система из двух проводников (обкладок, пластин), разделенных диэлектриком.

Конденсаторы обладают свойством накапливать на своих обкладках электрические заряды, равные по величине и противоположные по знаку.

Электрический заряд q каждой из обкладок пропорционален напряжению U между ними:

Величину С, равную отношению заряда одной из обкладок конденсатора к напряжению между ними, называют электрической емкостью конденсатора и выражают в фарадах (Ф).

Емкость конденсатора зависит от геометрических размеров, формы, взаимного расположения и расстояния между обкладками, а также от свойств диэлектрика.

Конденсаторы могут быть соединены последовательно, параллельно и смешанно (последовательно-параллельно).

При таком соединении на обкладках всех конденсаторов будут одинаковые по величине заряды:

Напряжения на конденсаторах будут различны, так как они зависят от их емкостей:

; …

Общее напряжение:

Общая, или эквивалентная, емкость

или

При параллельном соединении напряжение на всех конденсаторах одинаковое. Заряды на обкладках отдельных конденсаторов при различной их емкости:

, ….

Заряд, полученный всеми параллельно соединенными конденсаторами:

Общая (эквивалентная) емкость: С=С 1 +С 2 +С 3

Задание для практической работы

  1. Определить эквивалентную емкость батареи конденсаторов, соединенных по схеме, при соответствующих положениях ключей.

Источник

Практическая работа Конденсаторы.

Какую информацию может получить учащийся, взяв в руки конденсатор? Узнать электроёмкость конденсатора, максимальное напряжение, которое можно на него подавать, рассчитать заряд и энергию, которые данный конденсатор может накопить и др. Этому можно научиться, выполнив данную практическую работу

Просмотр содержимого документа
«Практическая работа Конденсаторы.»

ПРАКТИЧЕСКАЯ РАБОТА «КОНДЕНСАТОРЫ»

Три конденсатора различной емкости.

Пластина из диэлектрика.

(1) q– электрический заряд конденсатора

U – напряжение между обкладками

Энергия заряженного конденсатора:

(2)

Электроемкость плоского конденсатора:

ε – диэлектрическая проницаемость

(3) S – площадь пластин

d – толщина диэлектрика

Последовательное соединение конденсаторов:

(4)

Параллельное соединение конденсаторов:

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Рассмотрите выданные Вам конденсаторы, узнайте их электроемкость и напряжение, на которое они рассчитаны, запишите в таблицу.

Используя формулу (1), рассчитайте максимальный заряд, который могут накопить данные конденсаторы и запишите в таблицу.

Найдите максимальную энергию каждого конденсатора по формуле (2) и запишите в таблицу.

конденсатора

(Дж)

указанных на конденсаторе

(

)

Изготовьте модель простейшего плоского конденсатора, используя выданные Вам материалы, покажите преподавателю.

Выполнив необходимые измерения, рассчитайте электроемкость изготовленного Вами конденсатора, используя формулу(3) и таблицу «Диэлектрическая проницаемость веществ».

Начертите все возможные способы соединений ваших конденсаторов в батарею.

Рассчитайте электроемкость батареи в каждом случае, используя формулы (4) и (5), взяв данные из таблицы.

Все расчеты выполните в тетради.

Ответьте на вопросы:

а) какие виды конденсаторов Вам известны?

б) где и для чего используют конденсаторы?

10. При каком соединении конденсаторов: последовательном или параллельном, емкость батареи конденсаторов:

а) больше емкости каждого из конденсаторов? б) меньше емкости каждого из конденсаторов?

Источник

Практическая работа №2 последовательное и параллельное соединение конденсаторов

Цель работы: изучить особенности последовательного и параллельного соединения

Подготовка к работе:

При последовательном соединении конденсаторов:

1. Заряды, независимо от емкости равны:

, Кл

2. Общее напряжение:

, В

3. Напряжение на каждом конденсаторе:

; ;

4. Эквивалентная емкость находится из формулы

5. Энергия заряженного конденсатора:

, Дж

При параллельном соединении конденсаторов

, Кл

На всех конденсаторах – одно напряжение:

, В

Напряжение на каждом конденсаторе:

; ;

5. Энергия заряженного конденсатора:

Ход выполнения работы:

Начертить схему и переписать условие задачи.

Выписать из таблицы 1 то, что дано и то, что следует определить.

Решение необходимо выполнять по действиям с нумерацией и краткими пояснениями.

Источник

Практическая работа «Последовательное и параллельное соединение конденсаторов. Эквивалентные схемы»

Практическая работа по физике «Последовательное и параллельное соединение конденсаторов» Раздел 3 «Электродинамика» Тема 3.1 «Электростатика»

Просмотр содержимого документа
«Практическая работа «Последовательное и параллельное соединение конденсаторов. Эквивалентные схемы»»

Практическая работа № 24

Раздел 3 Электродинамика

Тема 3.1 Электростатика

Название практической работы: Последовательное и параллельное соединение конденсаторов. Эквивалентные схемы

Учебная цель: изучить распределение напряжения, зарядов в схемах с последовательным и параллельным соединением конденсаторов

Учебные задачи: определять эквивалентную ёмкость, заряд и энергию батареи конденсаторов по схеме.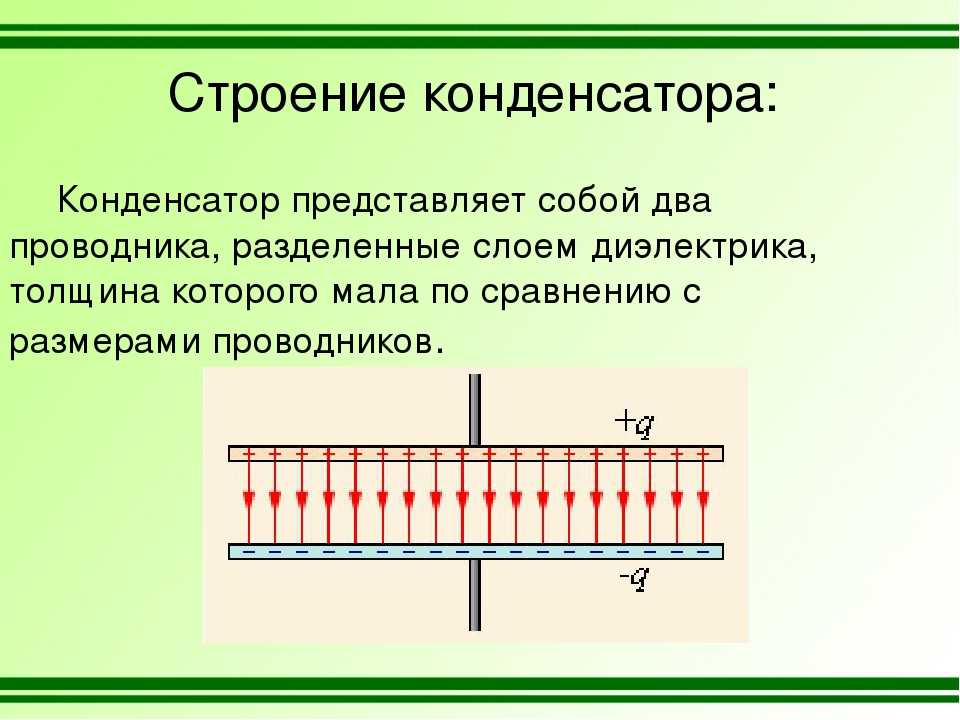 Определить напряжения и заряды на конденсаторах.

Правила безопасности: правила проведения в кабинете во время выполнения практического занятия

Норма времени: 2 часа

Образовательные результаты, заявленные во ФГОС третьего поколения:

уметь: вычерчивать схемы, определять эквивалентную ёмкость и заряд конденсаторов. Рассчитывать энергию батареи конденсаторов

знать: законы последовательного и параллельного соединения конденсаторов в батарею. Расчётные формулы ёмкости, заряда, напряжения, единицы измерения. Применение конденсаторов

— методические указания по выполнению практического занятия

— лабораторно-практическая тетрадь, карандаш, линейка

Порядок проведения занятия:

Для выполнения практической работы учебная группа распределяется по вариантам.

Конденсатор – система двух проводников (обкладок) разделённых слоем диэлектрика. Служит для накопления (конденсации) разделённых зарядов.

Плоский конденсатор – две плоские металлические пластины, расположенные параллельно и разделённые слоем диэлектрика. Обозначение конденсатора на электрических схемах соответствует его принципиальному устройству.

Электроёмкость конденсатора показывает, как много заряда может «натечь» в конденсатор, подключённый к источнику, разделяющему заряды.

Если это источник ЭДС равный

,то при соединении конденсатора и источника тока по схеме, рисунок 1, натекание заряда прекратиться,

когда напряжение на обкладках станет равно

Коэффициент пропорциональности между зарядом на конденсаторе Q и разностью потенциалов U на его обкладках называется электрической ёмкостью конденсатора С. Заряд на обкладках конденсатора тем больше, чем больше ЭДС источника

Важнейшей характеристикой любого конденсатора является его электрическая ёмкость С – физическая величина, равная отношению заряда Q конденсатора к разности потенциалов U между его обкладками:

Выражается в СИ в фарадах (Ф).

Ёмкость реальных конденсаторов гораздо меньше, и для её измерения обычно используют более мелкие единицы: 1 микрофарада (мкФ),

1нанофарада (нФ), 1 пикофарада (пФ)

Эквивалентной ёмкостью батареи конденсаторов называют такую ёмкость

С общ которая при подключении к тому же источнику тока принимает на себя такой же заряд, что и батарея конденсаторов.

Два конденсатора соединены параллельно, если обкладки обоих попарно соединены друг с другом, рисунок 2

Рисунок 2 Рисунок 4

У параллельного соединения конденсаторов ёмкости и заряды складываются, рисунок 2:

Для последовательного соединения конденсаторов, рисунок 4.

На практике конденсаторы включают только параллельно, можно представить это так, как будто площади их пластин складываются, складываются и их ёмкости. Последовательное соединение не имеет практического смысла, знание сложения необходимо только при анализе цепей переменного тока.

Проверка конденсаторов – перед проверкой конденсатор разряжают, то есть закорачивают его выводы на металлический предмет.

Энергия конденсатора. При зарядке конденсатора между обкладками скапливаются разделённые заряды (энергия электрического поля)

Эта энергия может быть высвобождена, если обкладки заряжённого конденсатора соединить через лампу накаливания. После того, как все заряды противоположного знака, скопленные на обкладках, протекут через спираль лампочки и прорекомбинируют, лампочка погаснет. Энергия конденсатора перейдёт во внутреннюю и световую энергию.

Для увеличения ёмкости радиотехнические конденсаторы изготавливают в виде двух слоёв алюминиевой фольги, проложенных промасленной бумагой (диэлектрик) и скрученных в многослойную пачку, упакованную в прочный корпус

Важной характеристикой конденсатора является максимальное напряжение Uмакс указанное на корпусе, при котором он сохраняет работоспособность. При больших напряжениях диэлектрик, проложенный между обкладками, пробивается, и обкладки замыкаются накоротко, составляя единый проводник. Чем больше напряжение, тем меньше ёмкость. В электролитических конденсаторах важно соблюдать полярность, иначе конденсатор выйдет из строя или возможен разрыв корпуса.

Конденсаторы используются в радиотехнике (излучение и приём электромагнитных волн, преобразование электромагнитных колебаний).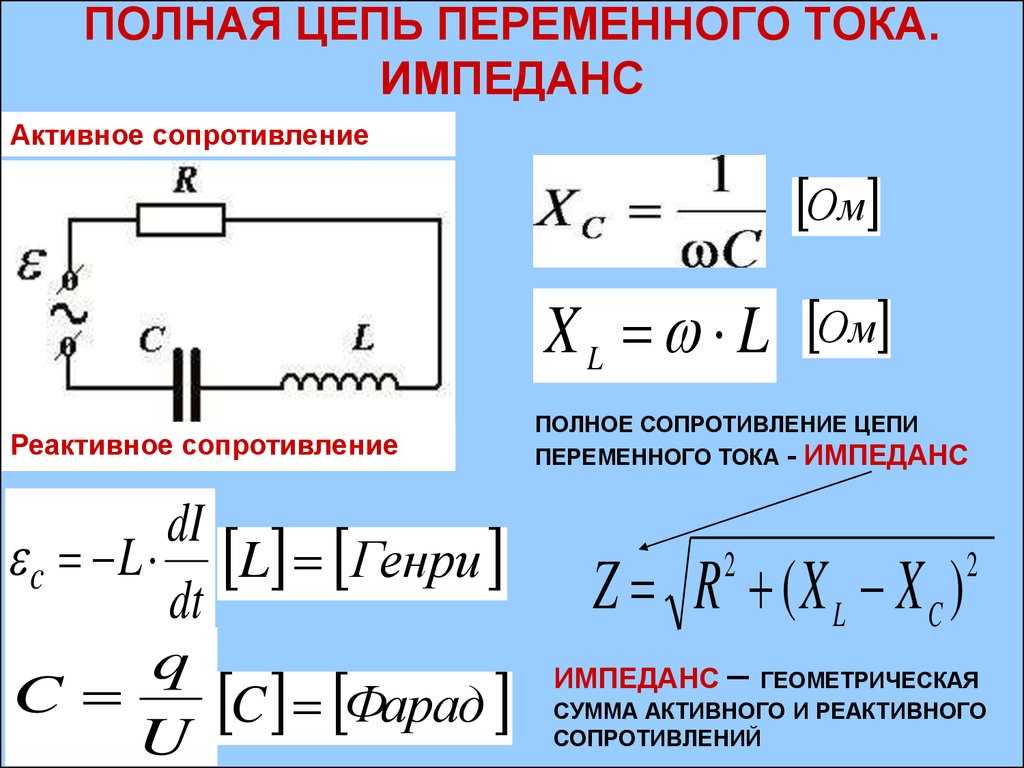 В устройствах, где нужно медленно накопить энергию, а затем быстро высвободить (фотовспышка, импульсный лазер).

Вопросы для закрепления теоретического материала к занятию:

1.Что такое эквивалентная ёмкость батареи конденсаторов?

2.Что значит, если два конденсатора соединены параллельно, последовательно?

3. Как рассчитываются ёмкости и заряды при параллельном и последовательном соединении конденсаторов?

4. Как рассчитывается энергия конденсатора?
5. Что значит закоротить конденсатор?

6. В каком случае необходимо применять последовательное соединение конденсаторов?

7. Что является важной характеристикой конденсатора, как технического устройства?

8. Где используется конденсатор?

9. Виды конденсаторов.

Содержание и Последовательность выполнения практической работы:

Задачи практической работы:

Вычертить схему №1 с учётом данных в таблице для своего варианта.

Определить эквивалентную ёмкость С, заряд Q батареи и энергию W, накопленную батареей.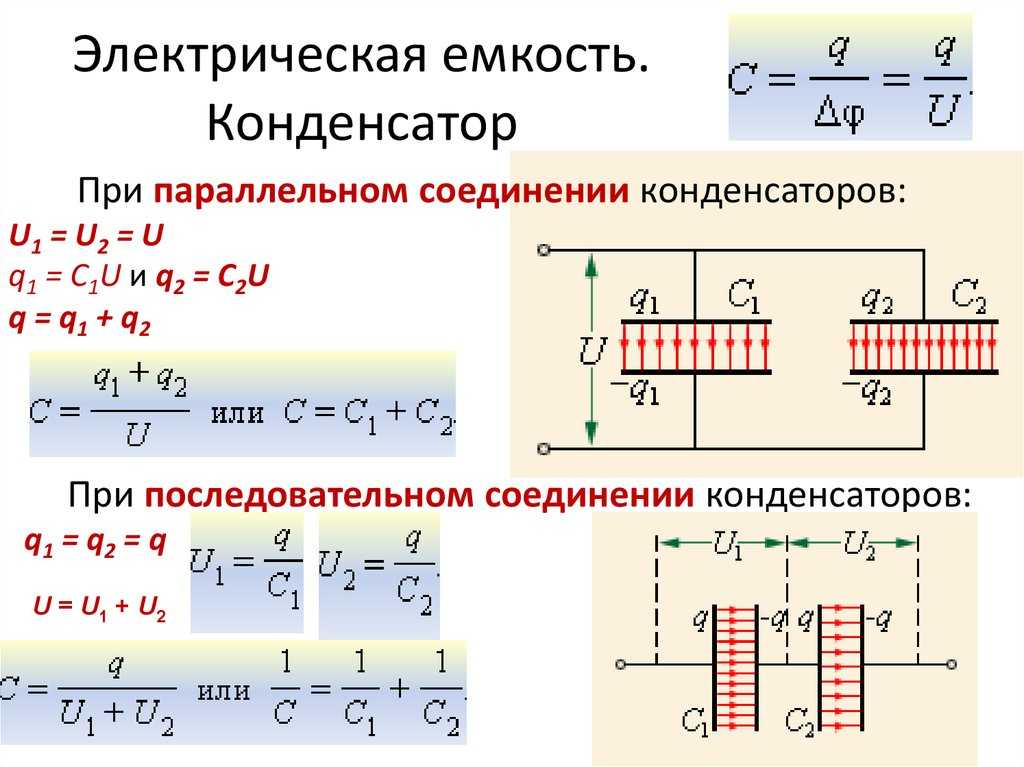

Вычислить напряжение и заряд на каждом конденсаторе. Как изменятся найденные величины, если один из конденсаторов закоротить? Напряжение на зажимах цепи U, взять из таблицы №1

Источник

Основы электрического конденсатора ~ Изучение электротехники

Конденсаторы представляют собой электрические устройства, обладающие емкостью. Конденсаторы противостоят изменениям напряжения с течением времени, создавая ток. Такое поведение делает конденсаторы полезными для стабилизации напряжения в цепях постоянного тока. Один из способов представить конденсатор в цепи постоянного тока — это временный источник напряжения, всегда «желающий» поддерживать напряжение на своих клеммах на одном уровне. Типичный конденсатор состоит из двух параллельных проводящих пластин, разделенных изолятором, называемым диэлектриком, как показано ниже:

Конденсатор с параллельными пластинами

Конденсаторы имеют номинальное напряжение, а также номинальную емкость. Различные символы, используемые для представления конденсаторов на схемах, показаны ниже:

Символы конденсации

емкость капитализации. электрический заряд. Чем больше емкость, тем больше сохраняется электрического заряда. Емкость плоского конденсатора определяется по формуле:

C = ЄA/d

Где:

C = емкость конденсатора в фарадеях (Ф). Единицами измерения могут быть микрофарды (мкФ) или пикофарады (пФ)

Є = электрическая проницаемость диэлектрического материала

A = площадь пластин конденсатора

d = расстояние между пластинами

Выходная емкость конденсатора увеличится, если используется более диэлектрический материал, либо если площадь пластин увеличена, либо если расстояние между пластинами уменьшено.

Поток постоянного тока через конденсатор :

Связь между напряжением и током в конденсаторе определяется выражением:

I = CdV/dt.

Когда конденсатор, который изначально разряжен, подключается к источнику постоянного напряжения, он имеет тенденцию потреблять большой ток. В процессе заряда напряжение на конденсаторе возрастает, а зарядный ток уменьшается. После того, как конденсатор получил достаточный заряд, напряжение на конденсаторе становится равным приложенному напряжению, и ток прекращается. После зарядки конденсатора это выглядит как обрыв в цепи постоянного тока.

Энергия, хранящаяся в конденсаторе

Энергия, хранящаяся в конденсаторе, дается:

E = ½ CV2 = 1/2QV

Конденсации в серии и параллель

. Замена капиталов. в параллели. Уменьшается при последовательном соединении конденсаторов:

C(параллельно) = C1+C2+…+Cn

C(последовательно) = 1/[1/C1 + 1/C2+ ….+1/Cn]

Поток переменного тока через конденсатор

Если переменное напряжение подается на чистый конденсатор, ток достигает максимума, когда напряжение начинает расти от нуля, и ток равен нулю, когда напряжение на конденсаторе максимально. Ток опережает приложенное напряжение на 90°, как показано ниже:

Вектор напряжения-тока конденсатора с переменным током через него.

Емкостное реактивное сопротивление

Противодействие протеканию переменного тока в чисто емкостной цепи, измеряемое в омах. Емкостное сопротивление находится по формуле:

Xc = 1/2πfC

Где:

Xc = емкостное реактивное сопротивление

f = частота

C = емкость

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    25141
    • Джеймс М. Фиоре
    • Муниципальный колледж Mohawk Valley

    Конденсатор — это устройство, хранящее энергию. Конденсаторы хранят энергию в виде электрического поля. В самом простом случае конденсатор может быть немного больше, чем пара металлических пластин, разделенных воздухом. Поскольку это представляет собой разомкнутую цепь, постоянный ток не будет течь через конденсатор. Если это простое устройство подключить к источнику постоянного напряжения, как показано на рис. 8.2.1.
    , отрицательный заряд будет накапливаться на нижней пластине, а положительный заряд накапливается на верхней пластине. Этот процесс будет продолжаться до тех пор, пока напряжение на конденсаторе не станет равным напряжению источника. При этом на пластинах будет накапливаться определенное количество электрического заряда.

    Рисунок 8.2.1
    : Базовый конденсатор с источником напряжения.

    Способность этого устройства накапливать заряд относительно возникающего на нем напряжения называется емкостью. Его символ — C, и он имеет единицы измерения фарад (F) в честь Майкла Фарадея, английского ученого 19-го века, который сделал ранние работы в области электромагнетизма. По определению, если общий заряд в 1 кулон связан с потенциалом в 1 вольт на пластинах, то емкость равна 1 фараду.

    \[1 \text{ фарад} \экв 1 \text{кулон} / 1 \text{вольт} \label{8.1} \]

    или чаще

    \[C = \frac{Q}{V} \label{8.2} \]

    Где

    \(C\) — емкость в фарадах,

    \(Q\) — заряд в кулонах,

    \(В\) — напряжение в вольтах.

    Из уравнения \ref{8.2} видно, что при любом заданном напряжении, чем больше емкость, тем большее количество заряда может быть сохранено. Мы также можем видеть, что при заданном размере конденсатора, чем выше напряжение, тем больше сохраняется заряд. Эти наблюдения относятся непосредственно к количеству энергии, которое может быть сохранено в конденсаторе. 92 \метка{8.3} \]

    Где

    \(Вт\) — энергия в джоулях,

    \(C\) — емкость в фарадах,

    \(В\) — напряжение в вольтах.

    Базовый конденсатор состоит из двух проводящих пластин, разделенных изолятором или диэлектриком. Этот материал может быть воздухом или изготовлен из различных материалов, таких как пластик и керамика. Это показано на рисунке 8.2.2.
    .

    Рисунок 8.2.2
    : Компоненты универсального конденсатора.

    Для практических конденсаторов пластины могут быть уложены попеременно или даже сделаны из фольги и сформированы в скрученную трубку. Какой бы ни была конструкция, характеристики диэлектрика будут играть главную роль в характеристиках устройства, как мы увидим.

    Как правило, емкость увеличивается прямо пропорционально площади пластины \(A\) и обратно пропорционально расстоянию между пластинами \(d\). Далее, это также пропорционально физической характеристике диэлектрика; диэлектрическая проницаемость \(\varepsilon\). Таким образом, емкость равна:

    \[C = \varepsilon \frac{A}{d} \label{8.4} \]

    Где

    \(C\) — емкость в фарадах,

    \(A\) — площадь плиты в квадратных метрах,

    \(d\) расстояние между пластинами в метрах,

    \(\varepsilon\) — диэлектрическая проницаемость диэлектрика между пластинами.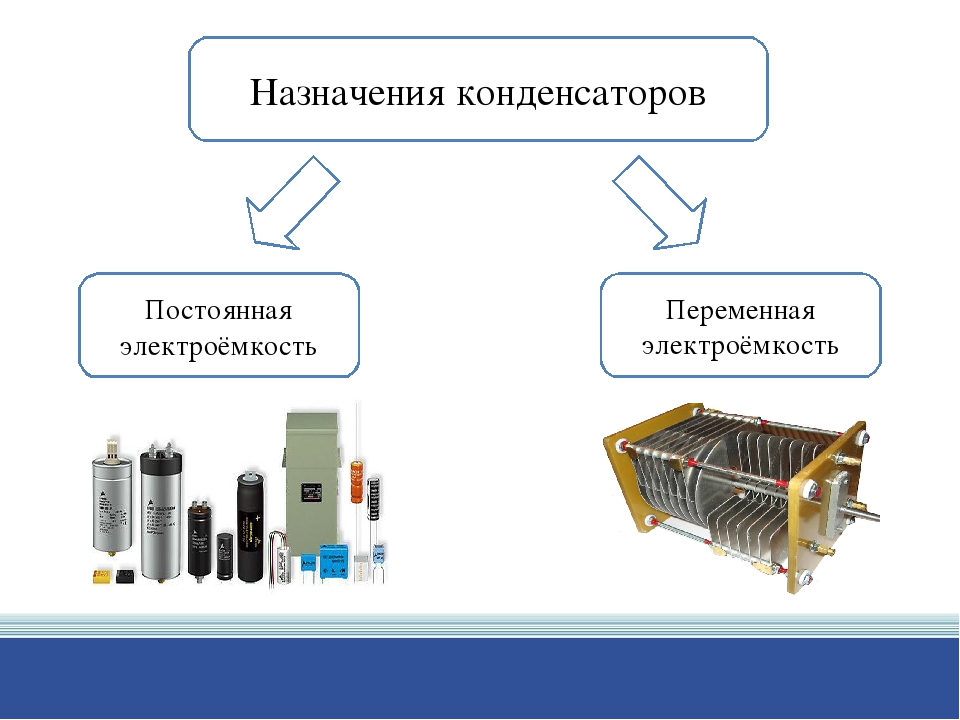

    Следует отметить, что эффективная площадь пластин несколько больше, чем точная физическая площадь пластин. Это происходит из-за явления, называемого окантовкой. По сути, линии электрического поля выпячиваются наружу на краях пластины, а не сохраняют однородную параллельную ориентацию. Это показано на рисунке 8.2.3.

    Рисунок 8.2.3
    : Конденсатор электрического поля с окантовкой.

    Из уравнения \ref{8.4} очевидно, что диэлектрическая проницаемость диэлектрика играет важную роль в определении объемного КПД конденсатора, другими словами, величины емкости, которая может быть упакована в компонент данного размера. Некоторые диэлектрики заметно более эффективны, чем другие. Для облегчения сравнения часто используется относительная диэлектрическая проницаемость, то есть отношение диэлектрической проницаемости к диэлектрической проницаемости вакуума \(\varepsilon_0\).

    Таблица относительной диэлектрической проницаемости различных диэлектриков приведена в таблице 8. 2.1.
    . Ряд обычных диэлектриков, таких как различные полипластиковые пленки и слюда, обладают диэлектрической проницаемостью, в два-шесть раз превышающей диэлектрическую проницаемость воздуха, но существуют также керамические диэлектрики, диэлектрическая проницаемость которых в сотни и тысячи раз больше, чем у воздуха.

    Материал Относительная диэлектрическая проницаемость, \(\varepsilon_r = \varepsilon /\varepsilon_0\)
    Вакуум 1 (\(\varepsilon_0\) =8,85E−12 фарад/метр)
    Воздух 1.00058986 (на СТП)
    ПТФЭ/тефлон 2. 1
    Полиэтилен/XLPE 2,25
    Полиимид 3,4
    Полипропилен 2,2-2,36
    Полистирол 2,4-2,7
    Полиэстер (майлар) 3.1
    Бумага 1,4
    Слюда 3-6
    Диоксид кремния 3,9
    Резина 7
    Алмаз 5,5-10
    Кремний 11,68
    Диоксид титана 86-173
    Титанат стронция 310
    Титанат кальция и меди >250 000
    Таблица 8. 2.1
    : Относительная диэлектрическая проницаемость различных диэлектриков. Данные взяты из Википедии и других источников.

    На первый взгляд может показаться, что выбор диэлектрика с самой высокой диэлектрической проницаемостью будет лучшим выбором, но это не обязательно так. Есть несколько других факторов, влияющих на это решение, включая температурную стабильность, сопротивление утечки (эффективное параллельное сопротивление), ESR (эквивалентное последовательное сопротивление) и прочность на пробой. Для идеального конденсатора сопротивление утечки было бы бесконечным, а ESR было бы равно нулю.

    В отличие от резисторов, конденсаторы не имеют максимальной рассеиваемой мощности. Вместо этого они имеют максимальное номинальное напряжение. Пробойная прочность диэлектрика устанавливает верхний предел того, насколько большое напряжение может быть приложено к конденсатору, прежде чем он будет поврежден. Пробойная прочность измеряется в вольтах на единицу расстояния, таким образом, чем ближе пластины, тем меньшее напряжение выдерживает конденсатор.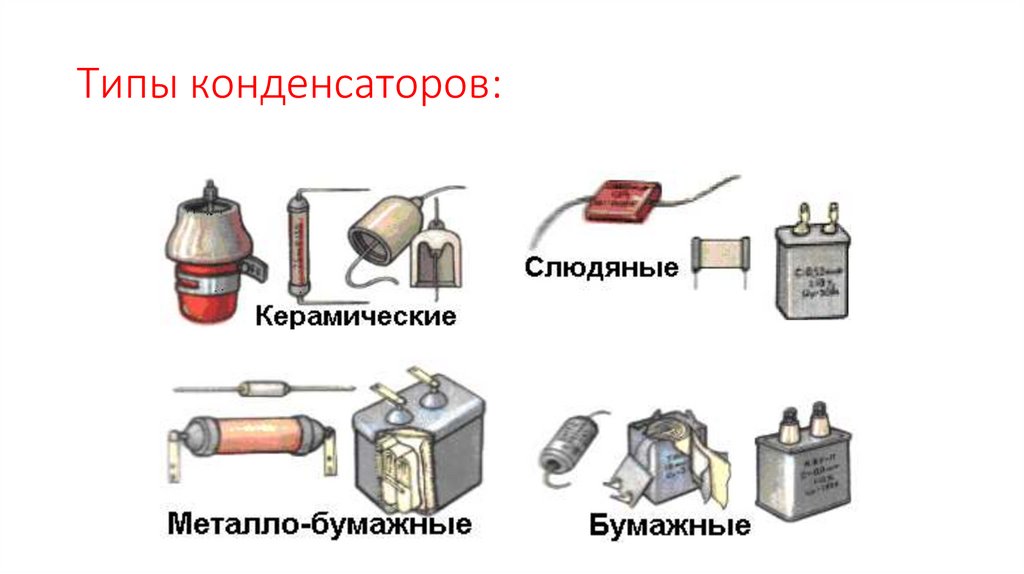 Например, уменьшение вдвое расстояния между пластинами удваивает емкость, но также вдвое снижает номинальное напряжение. Таблица 8.2.2
    перечисляет прочность на пробой различных диэлектриков. Сравнение таблиц Таблиц 8.2.1
    и 8.2.2
    намекает на сложность ситуации. Например, рассмотрим полистирол против полипропилена. Полистирол предлагает умеренно повышенную диэлектрическую проницаемость, но полипропилен имеет значительное преимущество с точки зрения прочности на разрыв. Как следствие, пластины могут быть размещены намного ближе друг к другу при использовании полипропилена, при этом достигается такое же номинальное напряжение, как у конденсатора с использованием полистирола. Следовательно, полипропиленовый конденсатор потребует меньшего объема при той же емкости. Дополнительным преимуществом полипропилена является, среди прочих характеристик, высокая термостойкость и низкое влагопоглощение. Сравнивая полипропилен с полиэфиром, мы обнаруживаем, что улучшенная диэлектрическая проницаемость полиэфира наряду с аналогичной прочностью на разрыв дает улучшенную объемную эффективность по сравнению с полипропиленом. К сожалению, полиэстер страдает от большей температурной зависимости.

    Вещество Прочность на разрыв (кВ/мм)
    Воздух 3,0
    Боросиликатное стекло 20-40
    ПТФЭ (тефлон, изоляционная пленка) 60-173
    Полиэтилен 19-160
    Полипропилен 650
    Полистирол 19,7
    PEEK (полиэфирэфиркетон) 23
    Полиэстер (майлар) 580
    Неопреновый каучук 15,7-26,7
    Вода дистиллированная 65-70
    Вощеная бумага 40-60
    Слюда 118
    Алмаз 2000
    ЦТС (керамика) 10-25
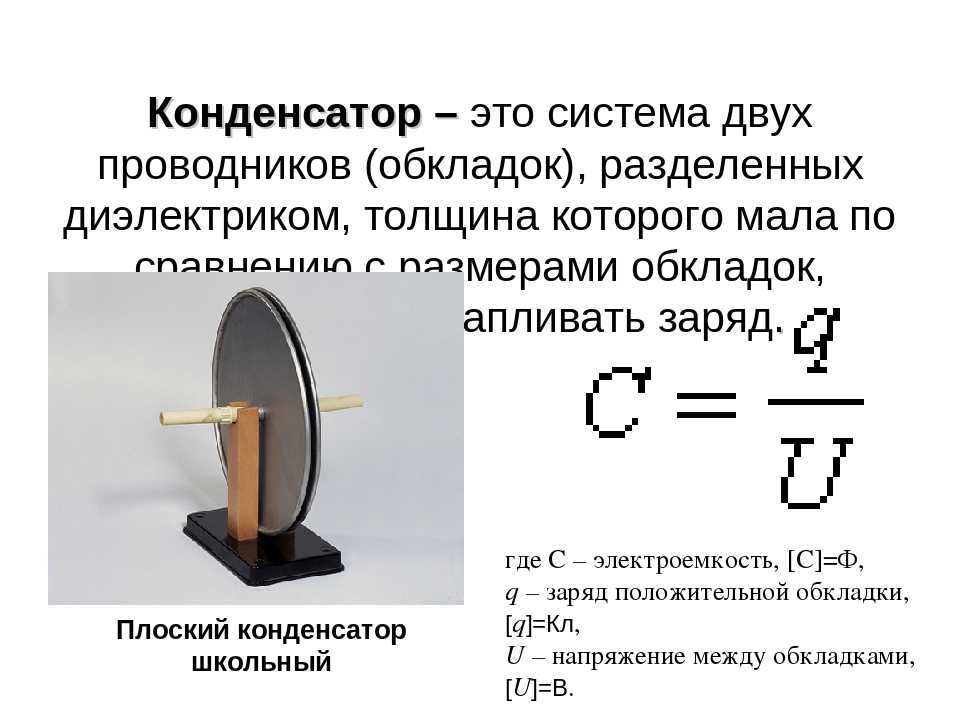    Таблица 8. {12}\). В отличие от резисторов, чей физический размер связан с их номинальной мощностью, а не значением сопротивления, физический размер конденсатора связан как с его емкостью, так и с его номинальным напряжением (следствие уравнения \ref{8.4}). Небольшие конденсаторы для поверхностного монтажа могут быть довольно малы, в то время как конденсаторы фильтра источника питания, обычно используемые в устройствах бытовой электроники, таких как аудиоусилитель, могут быть значительно больше, чем батарея элемента D. Выборка конденсаторов показана на рисунке 8.2.4.
    .

    Рисунок 8.2.4
    : Разнообразие стилей и упаковок конденсаторов.

    В передней и левой части фотографии находятся различные конденсаторы из пластиковой пленки. Дисковый конденсатор использует керамический диэлектрик. Небольшое квадратное устройство спереди представляет собой конденсатор для поверхностного монтажа, а справа от него находится каплевидный танталовый конденсатор, обычно используемый для обхода источника питания в электронных схемах. Конденсатор среднего размера справа со сложенными выводами представляет собой бумажный конденсатор, который когда-то был очень популярен в аудиосхемах. Некоторые конденсаторы имеют обжимное кольцо с одной стороны, включая большое устройство с винтовыми клеммами. Это алюминиевые электролитические конденсаторы. Эти устройства, как правило, демонстрируют высокий объемный КПД, но, как правило, не обеспечивают максимальной производительности в других областях, таких как абсолютная точность и ток утечки. Обычно они поляризованы, что означает, что выводы должны соответствовать полярности приложенного напряжения. Вставка их в цепь в обратном порядке может привести к катастрофическому отказу. Полярность обычно обозначается рядом знаков минус и/или полосой, обозначающей отрицательный вывод. Танталовые конденсаторы также поляризованы, но обычно обозначаются знаком плюс рядом с положительным выводом. Конденсатор переменной емкости, используемый для настройки радио, показан на рис. 8.2.5.
    . Один набор пластин крепится к раме, а пересекающийся набор пластин крепится к валу. Вращение вала изменяет площадь перекрытия пластин и, таким образом, изменяет емкость.

    Рисунок 8.2.5
    : Переменный конденсатор.

    Для больших конденсаторов значение емкости и номинальное напряжение обычно печатаются непосредственно на корпусе. В некоторых конденсаторах используется «MFD», что означает «микрофарады». Хотя цветовой код конденсатора существует, как и цветовой код резистора, он, как правило, теряет популярность. Для конденсаторов меньшего размера используется числовой код, повторяющий цветовой код. Обычно он состоит из трехзначного числа, например «152».

    Первые две цифры — это часть точности, а третья цифра — множитель в степени десяти. Результат в пикофарадах. Таким образом, 152 — это 1500 пф.

    Рисунок 8.2.6
    : Обозначения конденсаторов (сверху вниз): неполяризованные, поляризованные, переменные.

    Схематические обозначения конденсаторов показаны на рис. 8.2.6.
    . Широко используются три символа. Первый символ, использующий две параллельные линии для отражения двух пластин, предназначен для стандартных неполяризованных конденсаторов. Второй символ обозначает поляризованные конденсаторы. В этом варианте положительный вывод изображается прямой линией для этой пластины и часто обозначается знаком плюс. Минусовая клемма нарисована изогнутой линией. Третий символ используется для конденсаторов переменной емкости и прочерчен стрелкой, как реостат.

    Рисунок 8.2.7
    : Измеритель LCR, предназначенный для считывания емкости, сопротивления и индуктивности.

    Для получения точных измерений конденсаторов используйте измеритель LCR, такой как показанный на рис. 8.2.7.
    , может быть использовано. Эти устройства предназначены для измерения трех распространенных пассивных электрических компонентов: резисторов, конденсаторов и катушек индуктивности 1 . В отличие от простого цифрового мультиметра, измеритель LCR также может измерять значения на различных частотах переменного тока, а не только постоянного тока, а также определять вторичные характеристики, такие как эквивалентное последовательное сопротивление и эффективное сопротивление параллельной утечки.

    Спецификация конденсатора

    Часть типовой спецификации конденсатора показана на рис. 8.2.8.
    . Это серия металлизированных пленочных конденсаторов со сквозными отверстиями, в которых в качестве диэлектрика используется полипропилен. Сначала мы видим список общих функций. Во-первых, мы обнаружили, что в конденсаторах используется огнестойкое эпоксидное покрытие, а также они соответствуют требованиям RoHS. Затем мы переходим к набору технических характеристик электрических характеристик. Например, мы видим, что эта серия доступна в двух вариантах: один рассчитан на 800 вольт постоянного тока, а другой — на 1600 вольт постоянного тока. Кроме того, допуск доступен как \(\pm\)3% или \(\pm\)5%. Коэффициент рассеяния \((\tan \delta )\) представляет собой меру, имеющую особое значение для работы переменного тока и пропорциональную ESR (эквивалентное последовательное сопротивление, в идеале равное 0), чем меньше, тем лучше. Сопротивление изоляции указывает на значение эффективного сопротивления параллельной утечки (чем выше, тем лучше), здесь около 30 000 МОм\(\Омега\). Наконец, мы видим данные о физических размерах, необходимые для разводки печатных плат.

    Конденсаторы, включенные последовательно и параллельно

    Несколько конденсаторов, включенных последовательно и/или параллельно, ведут себя не так, как резисторы. Параллельное размещение конденсаторов увеличивает общую площадь пластины и, следовательно, увеличивает емкость, как показано в уравнении \ref{8.4}. Поэтому конденсаторы, включенные параллельно, увеличивают стоимость, ведя себя как резисторы, включенные последовательно. Напротив, когда конденсаторы расположены последовательно, расстояние между пластинами как бы увеличивается, что приводит к уменьшению емкости. Поэтому конденсаторы, включенные последовательно, ведут себя как резисторы, включенные параллельно. Их значение находится с помощью обратной суммы суммированных обратных величин или по правилу произведения-суммы.

    Рисунок 8.2.8
    : Паспорт конденсатора. Предоставлено Panasonic

    Пример 8.2.1

    Найдите эквивалентную емкость сети, показанной на рис. 8.2.9.
    .

    Рисунок 8.2.9
    : Схема для примера 8.2.1
    .

    Все эти конденсаторы соединены параллельно, поэтому эквивалентное значение равно сумме трех емкостей:

    \[C_{Всего} = C_1+C_2+C_3 \номер\]

    \[C_{Всего} = 1 \мкФ+100 нФ+560 нФ \номер\]

    \[C_{Всего} = 1,66 \мкФ \номер\]

    Пример 8.2.2

    Найдите эквивалентную емкость сети, показанной на рис. 8.2.10.
    .

    Рисунок 8.2.10
    : Схема для примера 8.2.2
    .

    В этой схеме мы видим, что левый и средний конденсаторы включены параллельно. Эта комбинация последовательно с конденсатором справа:

    \[C_{левый} = C_1+C_2 \номер\]

    \[C_{левый} = 3,3 \mu F+4,7 \mu F \номер \]

    \[C_{левый} = 8 \mu F \номер\]

    \[C_{Всего} = \frac{C_{левый}C_3} {C_{левый}+C_3} \номер\]

    \[C_{Всего} = \frac{8 \mu F16 \mu F}{8 \mu F+16 \mu F} \nonumber \]

    \[C_{Всего} \приблизительно 5,33 \мкФ \номер\]

    Если в цепи нет ничего, кроме источника напряжения, включенного параллельно с группой конденсаторов, напряжение будет одинаковым на всех конденсаторах, как и в резистивной параллельной цепи. Если вместо этого цепь состоит из нескольких конденсаторов, включенных последовательно с источником напряжения, как показано на рис. 8.2.11.
    , напряжение будет делиться между ними обратно пропорционально. Другими словами, чем больше емкость, тем меньше ее доля в приложенном напряжении. Напряжения также можно найти, сначала определив последовательную эквивалентную емкость. Затем общий заряд может быть определен с использованием приложенного напряжения. Наконец, отдельные напряжения рассчитываются по уравнению \ref{8.2}, \(V = Q/C\), где \(Q\) — общий заряд, а \(C\) — интересующая емкость. Это показано в следующем примере.

    Рисунок 8.2.11
    : простая последовательная схема, состоящая только из конденсаторов.

    Пример 8.2.3

    Найдите напряжения на конденсаторах на рис. 8.2.12.
    .

    Рисунок 8.2.12
    : Схема для примера 8.2.3
    .

    Первым шагом является определение общей емкости. Поскольку они расположены последовательно, мы можем использовать обратное правило:

    .

    \[C_{Всего} = \frac{1}{\frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}} \nonumber \]

    \[C_{Total} = \frac{1}{\frac{1}{2 \mu F} + \frac{1}{4 \mu F} + \frac{1}{8 \mu F}} \номер\]

    \[C_{Всего} \ приблизительно 1,143 \мкФ \номер\]

    Отсюда определяем общий заряд:

    \[Q = V C \номер\]

    \[Q = 12 V1.143 \mu F \номер \]

    \[Q = 13,71 мкм С \номер\]

    Заряд постоянен для всех последовательных конденсаторов, следовательно:

    \[V_{2uF} = \frac{Q}{C} \номер\]

    \[V_{2uF} = \frac{13.71 \mu C}{2 \mu F} \nonnumber \]

    \[В_{2 мкФ} = 6,855 В \номер\]

    \[V_{4uF} = \frac{Q}{C} \номер\]

    \[V_{4uF} = \frac{13.71 \mu C}{4 \mu F} \nonumber \]

    \[В_{4 мкФ} = 3,427 В \номер\]

    \[V_{8uF} = \frac{Q}{C} \номер\]

    \[V_{8uF} = \frac{13.71 \mu C}{8 \mu F} \nonumber \]

    \[V_{8uF} = 1.714V \номер\]

    Сумма трех напряжений составляет 12 вольт (в пределах погрешности округления) и соответствует ожидаемому значению KVL.

    Практический совет

    Хотя может возникнуть соблазн попробовать, не пытайтесь проверить работу примера 8.2.3.
    в лаборатории с помощью стандартного цифрового мультиметра. Причина в том, что внутреннее сопротивление типичного цифрового вольтметра на много порядков меньше, чем сопротивление утечки конденсаторов. В результате заряд будет передаваться счетчику, нарушая измерение. Это было бы похоже на попытку измерить напряжение на цепочке резисторов, каждый из которых превышает 100 МОм\(\Омега\), с помощью измерителя, внутреннее сопротивление которого равно 1 МОм\(\Омега\). Сопротивление измерителя доминирует над параллельной комбинацией и вызывает чрезмерную нагрузку, которая разрушает измерение. Для этих типов измерений необходим специальный тип вольтметра, электростатический вольтметр или электрометр. Их иногда называют счетчиками без взимания платы.

    Зависимость ток-напряжение

    Основная зависимость ток-напряжение конденсатора отличается от зависимости резистора. Конденсаторы не так сильно сопротивляются току; более продуктивно думать с точки зрения их реакции на это. Ток через конденсатор равен емкости, умноженной на скорость изменения напряжения на конденсаторе во времени (т. е. на его наклон). То есть важно не значение напряжения, а то, как быстро меняется напряжение. При фиксированном напряжении ток конденсатора равен нулю, и поэтому конденсатор ведет себя как открытый. Если напряжение меняется быстро, ток будет высоким, и конденсатор ведет себя скорее как короткое замыкание. Выражается формулой:

    \[i = C \frac{d v}{d t} \label{8.5} \]

    Где

    \(i\) — ток, протекающий через конденсатор,

    \(C\) — емкость ,

    \(dv/dt\) — скорость изменения напряжения конденсатора во времени.

    Особенно полезная форма уравнения \ref{8.5}:

    \[\frac{d v}{d t} = \frac{i}{C} \label{8.6} \]

    Альтернативный способ поиска в уравнении \ref{8.5} указывает, что если конденсатор питается от источника постоянного тока, напряжение будет расти с постоянной скоростью (\(dv/dt\)). Он непрерывно накапливает заряд на пластинах конденсатора со скоростью \(I\), что эквивалентно \(Q/t\). Пока присутствует ток, питающий конденсатор, напряжение на конденсаторе будет продолжать расти. Хорошая аналогия, если бы у нас была труба, льющая воду в резервуар, при этом уровень в резервуаре продолжает расти. Этот процесс накопления заряда на пластинах называется зарядкой конденсатора. Например, рассматривая схему на рис. 8.2.13.
    , мы видим источник тока, питающий один конденсатор. Если бы мы построили график зависимости напряжения конденсатора от времени, мы бы увидели график, подобный рисунку 8.2.14.
    .

    Рисунок 8.2.13
    : Конденсатор с источником тока.

    Рисунок 8.2.14
    : Напряжение конденсатора в зависимости от времени.

    С течением времени напряжение на конденсаторе увеличивается с положительной полярностью сверху вниз. С теоретически идеальными конденсатором и источником это будет продолжаться вечно или до тех пор, пока не будет отключен источник тока. В действительности эта линия либо начала бы отклоняться по горизонтали, когда источник достиг своих пределов, либо конденсатор вышел бы из строя, как только было бы достигнуто его напряжение пробоя. Наклон этой линии определяется размером источника тока и емкостью.

    Пример 8.2.4

    Определить скорость изменения напряжения на конденсаторе в цепи рис. 8.2.15
    . Также определите напряжение конденсатора через 10 миллисекунд после включения питания.

    Рисунок 8.2.15
    : Схема для примера 8.2.4
    .

    Во-первых, обратите внимание на направление источника тока. Это создаст отрицательное напряжение на конденсаторе сверху вниз. Скорость изменения:

    \[\frac{dv}{dt} = \frac{i}{C} \nonumber \]

    \[\frac{dv}{dt} = \frac{−5 \mu A}{30 нФ} \nonumber \]

    \[\frac{dv}{dt} \приблизительно −166,7 \text{ вольт в секунду} \nonumber \]

    Таким образом, каждую секунду напряжение повышается еще на -166,7 вольт. Если предположить, что он полностью разряжен при подаче питания, через 10 миллисекунд он возрастет до -166,7 В / с, умноженный на 10 мс, или -1,667 вольт.

    Уравнение \ref{8.6} дает представление о поведении конденсаторов. Как только что было отмечено, если конденсатор питается от постоянного источника тока, напряжение на нем возрастает с постоянной скоростью \(i/C\). Существует предел скорости изменения напряжения на конденсаторе. Мгновенное изменение означает, что \(dv/dt\) бесконечно, и, следовательно, ток, питающий конденсатор, также должен быть бесконечным (что невозможно). Это не проблема резисторов, которые подчиняются закону Ома, а ограничение конденсаторов. Поэтому мы можем указать особенно важную характеристику конденсаторов:

    \[\text{Напряжение на конденсаторе не может измениться мгновенно.} \label{8.7} \]

    Это наблюдение будет ключом к пониманию работы конденсаторов в цепях постоянного тока.

    Каталожные номера

    1 Катушки индуктивности рассматриваются в следующей главе.

    Эта страница под названием 8.2: Емкость и конденсаторы используется в соответствии с лицензией CC BY-NC-SA 4.

    Опубликовано

    в

    от

    admin

    Метки:

    Комментарии

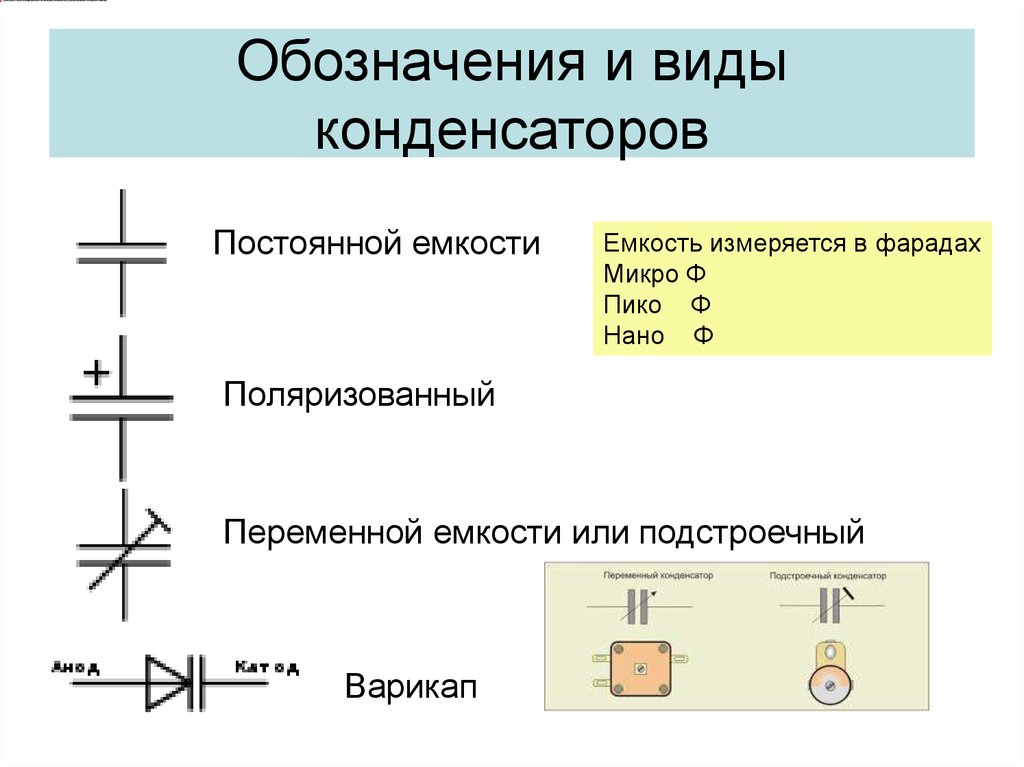
    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *