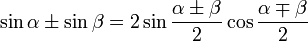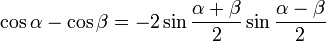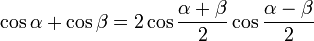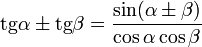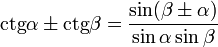Глоссарий. Алгебра и геометрия. Cos abТаблица Брадиса sin cos tg ctgКалькулятор поможет рассчитать точные значения тригонометрических функций sin, cos, tg и ctg для различных значений углов в градусах или радианах. На данной странице таблица Брадиса, которая дает значение sin, cos, tg, ctg любого острого угла, содержащего целое число градусов и десятых долей градуса. Для нахождения значения угла берется число на пересечении строки, которое соответствует числу градусов и столбца, которое соответствует числу минут. Например, sin 70°30' = 0.9426. Найти точное значениеТаблица Брадиса sin, cos
Таблица Брадиса tg, ctg
mozgan.ru Задание 6 — геометрия с элементами тригонометрии14 апреля 2011 Сегодня рассмотрим задачи B8 c тригонометрией в ее классическом понимании, где изучаются обычные прямоугольные треугольники. Поэтому никаких тригонометрических окружностей и отрицательных углов сегодня не будет — только обычные синусы и косинусы. Такие задачи составляют примерно 30% от общего числа. Помните: если в задаче B8 хоть раз упоминается угол π, она решается совсем другими способами. Мы обязательно рассмотрим их в ближайшее время. А сейчас — главное определение урока: Треугольник — фигура на плоскости, состоящая из трех точек и отрезков, которые их соединяют. Фактически, это замкнутая ломаная из трех звеньев. Точки называются вершинами треугольника, а отрезки — сторонами. Важно заметить, что вершины не должны лежать на одной прямой, иначе треугольник вырождается в отрезок. Довольно часто треугольником называют не только саму ломаную, но и часть плоскости, которая этой ломаной ограничена. Таким образом, можно определить площадь треугольника. Два треугольника называются равными, если один можно получить из другого путем одного или нескольких движений плоскости: сдвига, поворота или симметрии. Кроме того, существует понятие подобных треугольников: их углы равны, а соответствующие стороны пропорциональны... Все, что написано выше, можно было не читать. Потому что это не нужно. Вы что, не знаете, что такое треугольник? Вы действительно не знаете, как он выглядит? Хорошо, я сейчас покажу.
Это треугольник ABC. Более того, это прямоугольный треугольник: в нем ∠C = 90°. Именно такие чаще всего и встречаются в задаче B8. Все, что надо знать для решения задачи B8 — это несколько простых фактов из геометрии и тригонометрии, а также общая схема решения, в которой эти факты используются. Затем останется просто «набить руку». Начнем с фактов. Они разбиты на три группы:
Нельзя сказать, что какая-то из этих групп важнее, сложнее или проще. Но информация, которая в них содержится, позволяет решить любую задачу B8. Поэтому знать надо все. Итак, поехали! Группа 1: определения и следствия из них
Рассмотрим треугольник ABC, где ∠C — прямой. Для начала — определения: Синус угла — это отношение противолежащего катета к гипотенузе. Косинус угла — это отношение прилежащего катета к гипотенузе. Тангенс угла — это отношение противолежащего катета к прилежащему. Один угол или отрезок может входить в разные прямоугольные треугольники. Более того, очень часто один и тот же отрезок является катетом в одном треугольнике и гипотенузой — в другом. Но об этом — дальше, а пока будем работать с обычным углом А. Тогда:
Основные следствия из определения:
Хотите — верьте, хотите — нет, но этих фактов достаточно, чтобы решить примерно треть всех тригонометрических задач B8. Группа 2: основные тождестваПервое и самое главное тождество — теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Применительно к треугольнику ABC, рассмотренному выше, эту теорему можно записать так: AC 2 + BC 2 = AB 2 И сразу — небольшое замечание, которое убережет читателя от множества ошибок. Когда решаете задачу, всегда (слышите, всегда!) записывайте теорему Пифагора именно в таком виде. Не пытайтесь сразу выражать катет, как это обычно требуется. Возможно, вы сэкономите пару строчек вычислений, но именно на этой «экономии» было потеряно больше баллов, чем где-либо еще в геометрии. Второе тождество — из тригонометрии. Выглядит следующим образом: sin 2A + cos 2A = 1 Оно так и называется: основное тригонометрическое тождество. С его помощью можно через синус выразить косинус и наоборот. Группа 3: Симметрии в треугольникеТо, что написано ниже, относится только к равнобедренным треугольникам. Если в задаче таковой не фигурирует, то для решения достаточно фактов из первых двух групп.
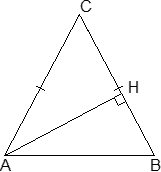
Итак, рассмотрим равнобедренный треугольник ABC, где AC = BC. Проведем к основанию высоту CH. Получим следующие факты:
Теперь, когда все факты рассмотрены, перейдем непосредственно к методам решения. Общая схема решения задачи B8Геометрия отличается от алгебры тем, что в ней нет простых и универсальных алгоритмов. Каждую задачу приходится решать с нуля — и в этом ее сложность. Тем не менее, общие рекомендации дать все-таки можно. Для начала, следует обозначить неизвестную сторону (если таковая имеется) за X. Затем применяем схему решения, которая состоит из трех пунктов:
Примеры решения задачА теперь попробуем с помощью полученных знаний решить наиболее распространенные задачи B8. Не удивляйтесь, что с таким арсеналом текст решения окажется не намного длиннее, чем исходное условие. И это радует :) Задача. В треугольнике ABC угол C равен 90°, AB = 5, BC = 3. Найдите cos A.
По определению (группа 1), cos A = AC : AB. Гипотенуза AB нам известна, а вот катет AC придется искать. Обозначим его AC = x. Переходим к группе 2. Треугольник ABC — прямоугольный. По теореме Пифагора: AC 2 + BC 2 = AB 2;x2 + 32 = 52;x2 = 25 − 9 = 16;x = 4. Теперь можно найти косинус: cos A = AC : AB = 4 : 5 = 0,8. Задача. В треугольнике ABC угол B равен 90°, cos A = 4/5, BC = 3. BH — высота. Найдите AH.
Обозначим искомую сторону AH = x и рассмотрим треугольник ABH. Он прямоугольный, причем ∠AHB = 90° по условию. Поэтому cos A = AH : AB = x : AB = 4/5. Это пропорция, ее можно переписать так: 5 · x = 4 · AB. Очевидно, мы найдем x, если будем знать AB. Рассмотрим треугольник ABC. Он также прямоугольный, причем cos A = AB : AC. Ни AB, ни AC нам не известны, поэтому переходим ко второй группе фактов. Запишем основное тригонометрическое тождество: sin 2A + cos 2A = 1; sin 2A = 1 − cos 2A = 1 − (4/5)2 = 1 − 16/25 = 9/25. Поскольку тригонометрические функции острого угла положительны, получаем sin A = 3/5. С другой стороны, sin A = BC : AC = 3 : AC. Получаем пропорцию: 3 : AC = 3 : 5; 3 · AC = 3 · 5;AC = 5. Итак, AC = 5. Тогда AB = AC · cos A = 5 · 4/5 = 4. Наконец, находим AH = x: 5 · x = 4 · 4;x = 16/5 = 3,2. Задача. В треугольнике ABC AB = BC, AC = 5, cos C = 0,8. Найдите высоту CH.
Обозначим искомую высоту CH = x. Перед нами равнобедренный треугольник ABC, в котором AB = BC. Следовательно, из третьей группы фактов имеем: ∠A = ∠C ⇒ cos A = cos C = 0,8 Рассмотрим треугольник ACH. Он прямоугольный (∠H = 90°), причем AC = 5 и cos A = 0,8. По определению, cos A = AH : AC = AH : 5. Получаем пропорцию: AH : 5 = 8 : 10; 10 · AH = 5 · 8;AH = 40 : 10 = 4. Осталось воспользоваться второй группой фактов, а именно теоремой Пифагора для треугольника ACH: AH 2 + CH 2 = AC 2; 42 + x2 = 52;x2 = 25 − 16 = 9;x = 3. Задача. В прямоугольном треугольнике ABC ∠B = 90°, AB = 32, AC = 40. Найдите синус угла CAD.
Поскольку нам известна гипотенуза AC = 40 и катет AB = 32, можно найти косинус угла A: cos A = AB : AC = 32 : 40 = 0,8. Это был факт из первой группы. Зная косинус, можно найти синус через основное тригонометрическое тождество (факт из второй группы): sin 2A + cos 2A = 1; sin 2A = 1 − cos 2A = 1 − 0,82 = 0,36; sin A = 0,6. При нахождении синуса вновь был использован тот факт, что тригонометрические функции острого угла положительны. Осталось заметить, что углы BAC и CAD смежные. Из первой группы фактов имеем: ∠BAC + ∠CAD = 180°; sin CAD = sin BAC = sin A = 0,6. Задача. В треугольнике ABC AC = BC = 5, AB = 8, CH — высота. Найдите tg A.
Треугольник ABC — равнобедренный, CH — высота, поэтому заметим, что AH = BH = 0,5 · AB = 0,5 · 8 = 4. Это факт из третьей группы. Теперь рассмотрим треугольник ACH: в нем ∠AHC = 90°. Можно выразить тангенс: tg A = CH : AH. Но AH = 4, поэтому остается найти сторону CH, которую обозначим CH = x. По теореме Пифагора (факт из группы 2) имеем: AH 2 + CH 2 = AC 2; 42 + x2 = 52;x2 = 25 − 16 = 9;x = 3. Теперь все готово, чтобы найти тангенс: tg A = CH : AH = 3 : 4 = 0,75. Задача. В треугольнике ABC AC = BC, AB = 6, cos A = 3/5. Найдите высоту AH.
Обозначим искомую высоту AH = x. Снова треугольник ABC — равнобедренный, поэтому заметим, что ∠A = ∠B, следовательно, cos B = cos A = 3/5. Это факт из третьей группы. Рассмотрим треугольник ABH. По условию, он прямоугольный (∠AHB = 90°), причем известна гипотенуза AB = 6 и cos B = 3/5. Но cos B = BH : AB = BH : 6 = 3/5. Получили пропорцию: BH : 6 = 3 : 5; 5 · BH = 6 · 3;BH = 18/5 = 3,6. Теперь найдем AH = x по теореме Пифагора для треугольника ABH: AH 2 + BH 2 = AB 2;x2 + 3,62 = 62;x2 = 36 − 12,96 = 23,04;x = 4,8. Дополнительные соображенияБывают нестандартные задачи, где рассмотренные выше факты и схемы бесполезны. Увы, в таком случае нужен действительно индивидуальный подход. Подобные задачи любят давать на всевозможных «пробных» и «демонстрационных» экзаменах. Ниже приведены две реальные задачи, которые предлагались на пробном ЕГЭ в Москве. Справились с ними единицы, что свидетельствует о высокой сложности этих задач. Задача. В прямоугольном треугольнике ABC из угла C = 90° провели медиану и высоту. Известно, что ∠A = 23°. Найдите ∠MCH.
Заметим, что медиана CM проведена к гипотенузе AB, поэтому M — центр описанной окружности, т.е. AM = BM = CM = R, где R — радиус описанной окружности. Следовательно, треугольник ACM — равнобедренный, и ∠ACM = ∠CAM = 23°. Теперь рассмотрим треугольники ABC и CBH. По условию, оба треугольника прямоугольные. Кроме того, ∠B — общий. Следовательно, треугольники ABC и CBH подобны по двум углам. В подобных треугольника соответствующие элементы пропорциональны. В частности: BCH = BAC = 23° Наконец, рассмотрим ∠C. Он прямой, и, кроме того, ∠C = ∠ACM + ∠MCH + ∠BCH. В этом равенстве ∠MCH — искомый, а ∠ACM и ∠BCH известны и равны 23°. Имеем: 90° = 23° + MCH + 23°;MCH = 90° − 23° − 23° = 44°. Задача. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
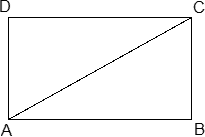
Обозначим стороны прямоугольника: AB = x, BC = y. Выразим периметр: PABCD = 2 · (AB + BC) = 2 · (x + y) = 34;x + y = 17. Аналогично выразим площадь: SABCD = AB · BC = x · y = 60. Теперь рассмотрим треугольник ABC. Он прямоугольный, поэтому запишем теорему Пифагора: AB 2 + BC 2 = AC2;AC 2 = x2 + y2. Заметим, что из формулы квадрата разности следует равенство: x2 + y2 = (x + y)2 − 2 · x · y = 172 − 2 · 60 = 289 − 120 = 169 Итак, AC 2 = 169, откуда AC = 13. Смотрите также:
www.berdov.com Тригонометрические выражения и тригонометрические формулы [wiki.eduVdom.com]subjects:mathematics:тригонометрические_выражения_и_формулы Отметим на координатной оси Ох справа от точки О точку А и построим окружность с центром в точке О и радиусом ОА (так называемым начальным радиусом). Окружность с центром в точке О и радиусом ОАРис.1 Пусть при повороте на угол a против часовой стрелки начальный радиус ОА переходит в радиус ОВ. Тогда:
Если координаты точки В равны x и y, то: $$\sin{\alpha} = \frac{y}{R}\;;\; \cos{\alpha} = \frac{x}{R}\;;\; {\rm tg}\, \alpha = \frac{y}{x}\;;\; {\rm ctg}\, \alpha = \frac{x}{y}$$ Таблица значений sin α, cos α, tg α, ctg αПриведем таблицу значений тригонометрических функций некоторых углов (прочерк сделан, когда выражение не имеет смысла):
Свойства sin, cos, tg и ctgСвойства синуса (sin), косинуса (cos), тангенса(tg) и котангенса(ctg):
1 радиан - это мера центрального угла, которому соответствует длина дуги, равная длине радиуса окружности. Связь радианов с градусами: $1° =\frac{\pi}{180}\text{рад; 1 рад }=\frac{180°}{\pi}$. Основные тригонометрические тождества
Формулы приведения
Формулы сложения
Формулы двойного углаФормулы двойного угла или двойного аргумента:
Формулы половинного аргументаФормулы половинного аргумента (для sin и cos - формулы понижения степени):
Формулы суммы и разности
Формулы произведения
Соотношения между sin x, cos x и tg(x/2)Один из способов использования: свести всё к tg(x/2) и путём замены получить обычное алгебраическое выражение.
Простейшие тригонометрические уравнения
Дополнительноsubjects/mathematics/тригонометрические_выражения_и_формулы.txt · Последние изменения: 2014/02/26 22:10 — ¶ wiki.eduvdom.com Все формулы по тригонометрииВсе формулы по тригонометрииОсновные тригонометрические тождества\(sin^2x+cos^2x=1\) \(tgx= \frac{sinx}{cosx}\) \(ctgx= \frac{cosx}{sinx}\) \(tgxctgx=1\) \(tg^2x+1= \frac{1}{cos^2x}\) \(ctg^2x+1= \frac{1}{sin^2x}\) Формулы двойного аргумента (угла)\(sin2x=2cosxsinx\) \(sin2x= \frac{2tgx}{1+tg^2x}= \frac{2ctgx}{1+ctg^2x} = \frac{2}{tgx+ctgx}\) \(cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x\) \(cos2x= \frac{1-tg^2x}{1+tg^2x}= \frac{ctg^2x-1}{ctg^2x+1}= \frac{ctgx-tgx}{ctgx+tgx} \) \(tg2x= \frac{2tgx}{1-tg^2x}= \frac{2ctgx}{ctg^2x-1}= \frac{2}{ctgx-tgx}\) \(ctg2x= \frac{ctg^2x-1}{2ctgx}= \frac{ctgx-tgx}{2}\) Формулы тройного аргумента (угла)\(sin3x=3sinx-4sin^3x\) \(cos3x=4cos^3x-3cosx\) \(tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}\) \(ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}\) Формулы половинного аргумента (угла)\(sin^2 \frac{x}{2}= \frac{1-cosx}{2}\) \(cos^2 \frac{x}{2}= \frac{1+cosx}{2}\) \(tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}\) \(ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}\) \(tg \frac{x}{2}= \frac{1-cosx}{sinx}= \frac{sinx}{1+cosx}\) \(ctg \frac{x}{2}= \frac{1+cosx}{sinx}= \frac{sinx}{1-cosx}\) Формулы квадратов тригонометрических функций\(sin^2x= \frac{1-cos2x}{2}\) \(cos^2x= \frac{1+cos2x}{2}\) \(tg^2x= \frac{1-cos2x}{1+cos2x}\) \(ctg^2x= \frac{1+cos2x}{1-cos2x}\) \(sin^2 \frac{x}{2}= \frac{1-cosx}{2}\) \(cos^2 \frac{x}{2}= \frac{1+cosx}{2}\) \(tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}\) \(ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}\) Формулы кубов тригонометрических функций\(sin^3x= \frac{3sinx-sin3x}{4}\) \(cos^3x= \frac{3cosx+cos3x}{4}\) \(tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}\) \(ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}\) Формулы тригонометрических функций в четвертой степени\(sin^4x= \frac{3-4cos2x+cos4x}{8}\) \(cos^4x= \frac{3+4cos2x+cos4x}{8}\) Формулы сложения аргументов\(sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta\) \(cos(\alpha + \beta) = cos \alpha cos \beta - sin \alpha sin \beta \) \(tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 - tg \alpha tg \beta}\) \(ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}\) \(sin(\alpha - \beta) = sin \alpha cos \beta - cos \alpha sin \beta\) \(cos(\alpha - \beta) = cos \alpha cos \beta + sin \alpha sin \beta\) \(tg(\alpha - \beta)= \frac{tg \alpha - tg \beta}{1 + tg \alpha tg \beta}\) \(ctg(\alpha - \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha - ctg \beta}\) Формулы суммы тригонометрических функций\(sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha - \beta }{2}\) \(cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha - \beta }{2}\) \(tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta} \) \(ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}\) \((sin\alpha + cos\alpha)^2= 1+sin2\alpha \) Формулы разности тригонометрических функций\(sin\alpha - sin\beta = 2sin \frac{\alpha - \beta }{2} \cdot cos \frac{\alpha + \beta }{2}\) \(cos\alpha - cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha - \beta }{2}\) \(tg\alpha - tg\beta = \frac{sin(\alpha - \beta) }{cos \alpha cos \beta} \) \(ctg\alpha - ctg\beta = - \frac{sin(\alpha - \beta) }{sin \alpha sin \beta}\) \((sin\alpha + cos\alpha)^2= 1-sin2\alpha \) Формулы произведения тригонометрических функций\(sin\alpha \cdot sin\beta = \frac{cos(\alpha - \beta)-cos(\alpha + \beta)}{2}\) \(sin\alpha \cdot cos\beta = \frac{sin(\alpha - \beta)+sin(\alpha + \beta)}{2}\) \(cos\alpha \cdot cos\beta = \frac{cos(\alpha - \beta)+cos(\alpha + \beta)}{2}\) \(tg\alpha \cdot tg\beta = \frac{cos(\alpha - \beta)-cos(\alpha + \beta)}{cos(\alpha - \beta)+cos(\alpha + \beta)} = \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta}\) \(ctg\alpha \cdot ctg\beta = \frac{cos(\alpha - \beta)+cos(\alpha + \beta)}{cos(\alpha - \beta)-cos(\alpha + \beta)} = \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta}\) \(tg\alpha \cdot ctg\beta = \frac{sin(\alpha - \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha - \beta)}\) 100formul.ru Формулы тригонометрических уравненийДля удобной работы все формулы для решения простейших тригонометрических уравнений, включая частные случаи, а также таблицы арксинусов, арккосинусов, арктангенсов и арккотангенсов собраны на одной странице. I. sin x =a При │a│>1 это уравнение решений не имеет. При │a│не превосходящем 1 уравнение имеет бесконечное множество решений: Таблица арксинусов II. cos x=a При │a│>1 это уравнение решений не имеет. При │a│не превосходящем 1 уравнение имеет бесконечное множество решений: Таблица арккосинусов Частные случаи синуса и косинуса:
III. tg x=a Уравнение имеет бесконечное множество решений при любых значениях a. Таблица арктангенсов IV. ctg x = a Уравнение имеет бесконечное множество решений при любых значениях a. Таблица арккотангенсов
www.uznateshe.ru cos 2Единичная окружность помогает разобраться, чему равны cos 1, cos 2, cos 3, cos 4, cos 5 и cos 6, без калькулятора и таблиц.
Чтобы найти углы в 1, 2, 3, 4 5 и 6 радиан на единичной окружности, можно вспомнить, что п приближенно равно 3,14, и привязать их местонахождение к п, п/2, 3п/2 и 2п. Можно пойти другим путем: угол в 1 радиан соответствует длине дуги, равной радиусу окружности. Соответственно, отмечаем 6 раз на окружности длину радиуса. Конечно, рисунок получается очень приблизительным, но наглядным. Итак, косинус 1, косинус 2, косинус 3, косинус 4, косинус 5 и косинус 6 — это абсциссы (x) отмеченных точек. С помощью единичной окружности можно легко сравнивать косинусы. Мы видим, cos 1>0, cos 5>0 и cos 6>0, а cos 2<0, cos 3<0, cos 4<0. Соответственно, вопрос сравнения косинусов с разными знаками решается элементарно: любое положительное число больше любого отрицательного: например, cos1 > cos3. При сравнении косинусов с одинаковыми знаками можно использовать геометрическую интерпретацию. Таким образом получаем, например: cos2 > cos4, cos5 < cos1. Если нужны более точные значения cos 1, cos 2, cos 3, cos 4, cos 5 и cos 6, можно воспользоваться калькулятором либо таблицами: При оценке приблизительных значений углов, больших 6 радиан, геометрическая интерпретация тоже работает, но с увеличением угла накапливается погрешность вычислений. www.uznateshe.ru Тригонометрические формулы. Основные тригонометрические тождества. Тригонометрические тождестваОсновные тригонометрические тождества
Формулы сложения
Формулы двойного угла
Формулы тройного угла
Формулы понижения степени
Переход от произведения к сумме
Переход от суммы к произведению Другие заметки по алгебре и геометрии edu.glavsprav.ru | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||
|
|
||||||||||||||||||
|








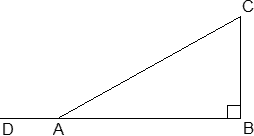




![Rendered by QuickLaTeX.com \[x = {( - 1)^n}\arcsin a + \pi n,(n \in Z)\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-afa5e220d00b2dfad5e167095225088c_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{c}} a&{ - 1}&{ - \frac{{\sqrt 3 }}{2}}&{ - \frac{{\sqrt 2 }}{2}}&{ - \frac{1}{2}}&0&{\frac{1}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 3 }}{2}}&1 \\ {\arcsin a}&{ - \frac{\pi }{2}}&{ - \frac{\pi }{3}}&{ - \frac{\pi }{4}}&{ - \frac{\pi }{6}}&0&{\frac{\pi }{6}}&{\frac{\pi }{4}}&{\frac{\pi }{3}}&{\frac{\pi }{2}} \end{array}\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-dddd0c1275fb0e70d61f82bcf54a9696_l3.png)
![Rendered by QuickLaTeX.com \[\arcsin ( - a) = - \arcsin a\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-e1b3c14f02fd7be613fa70ec7986f8a1_l3.png)
![Rendered by QuickLaTeX.com \[x = \pm \arccos a + 2\pi n,(n \in Z).\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ea811d33f0b5c5702c4257d8c8029338_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{c}} a&{ - 1}&{ - \frac{{\sqrt 3 }}{2}}&{ - \frac{{\sqrt 2 }}{2}}&{ - \frac{1}{2}}&0&{\frac{1}{2}}&{\frac{{\sqrt 2 }}{2}}&{\frac{{\sqrt 3 }}{2}}&1 \\ {\arccos a}&\pi &{\frac{{5\pi }}{6}}&{\frac{{3\pi }}{4}}&{\frac{{2\pi }}{3}}&{\frac{\pi }{2}}&{\frac{\pi }{3}}&{\frac{\pi }{4}}&{\frac{\pi }{6}}&0 \end{array}\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d6205822282bdbc10f4182955ede6725_l3.png)
![Rendered by QuickLaTeX.com \[\arccos ( - a) = \pi - \arccos a\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-23515b667c9c7ca80dea1b0ea4dfcd9d_l3.png)

![Rendered by QuickLaTeX.com \[x = arctga + \pi n,(n \in Z).\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-3e678a7de90e933e5879597654e902f4_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{c}} a&{ - \sqrt 3 }&{ - 1}&{ - \frac{{\sqrt 3 }}{3}}&0&{\frac{{\sqrt 3 }}{3}}&1&{\sqrt 3 } \\ {arctga}&{ - \frac{\pi }{3}}&{ - \frac{\pi }{4}}&{ - \frac{\pi }{6}}&0&{\frac{\pi }{6}}&{\frac{\pi }{4}}&{\frac{\pi }{3}} \end{array}\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-c4cd279b427e1eb10057343923bbc846_l3.png)
![Rendered by QuickLaTeX.com \[arctg( - a) = - arctga\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-200cb34e4f744acd92eb5ddbd06db977_l3.png)
![Rendered by QuickLaTeX.com \[x = arcctga + \pi n,(n \in Z).\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-0230b4cd13a6561f764c2aea4200dea0_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{c}} a&{ - \sqrt 3 }&{ - 1}&{ - \frac{{\sqrt 3 }}{3}}&0&{\frac{{\sqrt 3 }}{3}}&1&{\sqrt 3 } \\ {arcctga}&{\frac{{5\pi }}{6}}&{\frac{{3\pi }}{4}}&{\frac{{2\pi }}{3}}&{\frac{\pi }{2}}&{\frac{\pi }{3}}&{\frac{\pi }{4}}&{\frac{\pi }{6}} \end{array}\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-8ec4a8426257342cf6dbca07004c66a0_l3.png)
![Rendered by QuickLaTeX.com \[\operatorname{arcc} tg( - a) = \pi - \operatorname{arcc} tga\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-232f2ca5ba57cbb36a0ec0689c4b1112_l3.png)

![Rendered by QuickLaTeX.com \[\cos 1 \approx 0,5403\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-3ed80b6cc0ee9f22d5f589bd9754a1a0_l3.png)
![Rendered by QuickLaTeX.com \[\cos 2 \approx - 0,4161\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-2bc018e3544872563ccc594f5d0c727e_l3.png)
![Rendered by QuickLaTeX.com \[\cos 3 \approx - 0,99\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-13f914b4c383ac7f0434d708b4e23820_l3.png)
![Rendered by QuickLaTeX.com \[\cos 4 \approx - 0,6536\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-aa784fde2f8d3cfcec09fc452af35513_l3.png)
![Rendered by QuickLaTeX.com \[\cos 5 \approx 0,2835\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-62b2089177e3af4c19fc6680031f03db_l3.png)
![Rendered by QuickLaTeX.com \[\cos 6 \approx 0,9602.\]](/800/600/http/www.uznateshe.ru/wp-content/ql-cache/quicklatex.com-50387b735984970f375ccde907006921_l3.png)