Что такое активная нагрузка в цепи переменного тока: Цепь переменного тока с активной нагрузкой

28) Цепь переменного тока с активной нагрузкой.

Если к активному
сопротивлениюR приложить
синусоидальное напряжение

то в электр, цепи
возникнет синусоидальный ток

(
измен-ся также по синусоидальному
закону), совпадающий по фазе с напряжением.

I=U/
R=(Umsin(wt))/R=Im*sin(wt)

На
участке с активным сопротивлением
напряжение и ток совпадают по фазе.

Мгновенное
значение напряжения и тока комплексные
значения в показательной форме:

;

;

;

Закон
Ома в комплексной форме для участка
цепи содержащий активное сопротивление.

29) Цепь переменного тока с индуктивной нагрузкой

В
электрической цепи sin-го тока содержащей
катушку индуктивности L под действием
изменяющегося sin-ого напряжения

в цепи возникает ток

изменяющийся по sin-му закону отстающий
по фазе от напряжения на угол

.
Докажем это:

;

— индуктивное
сопротивление

[Ом] ;

;

Определим
сдвиг фаз между током и напряжением

График
мгновенных значений:

Векторная
диаграмма I, U

Заменим
мгновенные значения U, I их комплексными
выражениями в показательной форме

;

;

По
закону Ома определим комплексное
сопротивление цепи

;

индуктивная проводимость

активная проводимость – G

В
цепи с индуктивным сопротивлением сила
тока отстает от напряжения на 90 градусов.

30) Емкостное сопротивление

Электрическое
устройство обратимо преобразующее
энергию источника тока в энергию
электрического поля конденсатора
называют емкостным сопротивлением.

Конденсатор в цепи
переменного тока обладает емкостным
сопротивлением. 

При включении
конденсатора в цепь постоянного
напряжения (рис. 1) сила тока I = 0,
а при включении конденсатора в цепь
переменного напряжения (рис. 2) сила
тока I   0. Следовательно,
конденсатор в цепи переменного напряжения
создает сопротивление меньше, чем в
цепи постоянного тока.

рис. 1

рис. 2

Мгновенное
значение напряжения равно:

Мгновенное
значение силы тока равно:

или

, 

где U₀
C = I₀. Следовательно,

Таким образом,
колебания напряжения отстают от
колебаний тока по фазе на  /2 (рис. 3).

рис. 3

Емкостное
сопротивление равно:

так как I₀ = U₀
C. Величина емкостного
сопротивления так как величина емкостного
сопротивления обратно пропорциональна
произведению электроемкости конденсатора
и циклической частоты переменного тока.

Физический смысл:
емкостное сопротивление обусловлено
протеканием токов зарядки и разрядки
конденсатора, т. е. изменению переменного
тока в любое мгновение противодействует
электрическое поле между обкладками
конденсатора.

Мощность равна

P = IUcos

При  = /2
мощность P = 0, так как идет
обмен энергией между источником
напряжения и емкостным потребителем.

рис. 4

Резонанс в
электрической цепи – явление резкого
возрастания амплитуды вынужденных
колебаний тока при совпадении частот
 ₀ =  ,
где  ₀ – собственная частота
колебательного контура;  – частота
питающего напряжения в цепи (рис. 4).
Поскольку

,

а X_L~
, то I в цепи будет зависеть от  и
будет максимален при частоте, отвечающей
условию:

X_C=X_L

Когда

,
в цепи наблюдается резонанс.

рис. 4

Амплитуда
установившихся колебаний тока будет
определяться уравнением

.

Если

,
то при R 0 I  .

Зависимость тока
в колебательном контуре от частоты при
двух значениях R, где R₂>R₁
(рис.  5).

рис. 5

Электрические цепи переменного тока

Переменный ток получил гораздо большее распространение в промышленности и в быту, чем постоянный, так как упрощается конструкция электродвигателей, а синхронные генераторы могут быть выполнены на значительно большие мощности и более высокие напряжения, чем генераторы постоянного тока. Переменный ток позволяет легко изменять величину напряжения с помощью трансформаторов, что необходимо при передаче электроэнергии на большие расстояния.

Электрический ток, возникающий под действием э. д. с, которая изменяется по синусоидальному закону, называют переменным. По существу, переменный ток — это вынужденные колебания тока в электрических цепях.
Амплитудой переменного тока называется наибольшее значение, положительное или отрицательное, принимаемое переменным током.
Периодом называется время, в течение которого происходит полное колебание тока в проводнике.
Частота — величина, обратная периоду.
Фазой называется угол

или , стоящий под знаком синуса. Фаза характеризует состояние переменного тока с течением времени. При t=0 фаза называется начальной.
Периодический режим: . К такому режиму может быть отнесен и синусоидальный:

где

— амплитуда;
— начальная фаза;
— угловая скорость вращения ротора генератора.
При f=50Гц T= 1/f=0,02 с, 314рад/с.

График синусоидальной функции называется волновой диаграммой.

Расчет цепей переменного тока с использованием мгновенных значений тока, напряжения и ЭДС требует громоздкой вычислительной работы. Поэтому изменяющиеся непрерывно во времени токи, напряжения и ЭДС заменяют эквивалентными во времени величинами.
При расчете электрических цепей синусоидальную функцию выражают по формуле Эйлера через экспоненциальные функции:

где

Тогда

где

— поворотный множитель;
— комплексная амплитуда напряжения;
— сопряженная комплексная амплитуда напряжения.

Таким образом, синусоидальное напряжение можно представить на комплексной плоскости вращающимся вектором. Тогда амплитудное значение напряжения

будет представлять собой модуль или длину вектора напряжения.

Вектор напряжения на комплексной плоскости
Так как в цепи с синусоидальным напряжением ток тоже будет подчиняться этому закону, то аналогично можно записать

где

— комплексная амплитуда тока; *
— сопряженная комплексная амплитуда тока.
Разделив напряжение на ток, получим закон Ома в комплексном виде:

При

напряжение на сопротивлении согласно закону Ома . Таким образом, следует отметить, что на активном сопротивлении напряжение и ток совпадают по фазе и (см. рисунок).

Кривые напряжения и тока в активном сопротивлении

Величину переменного напряжения или тока можно оценить значением амплитуды или средним значением за полупериод или действующим значением. При изменении напряжения или тока по закону синуса среднее значение напряжения определяется:

При большой частоте вращения ротора генератора, т. е. при большой частоте колебаний э. д. с. и силы тока, измерять их амплитуды на практике крайне неудобно. По этой причине ввели величины, названные действующими значениями э. д. с, силы тока и напряжения.
Действующим значением силы переменного тока называют силу такого постоянного тока, при прохождении которого по той же цепи и за то же время выделяется такое же количество теплоты, как и при прохождении переменного тока.

откуда

При синусоидальном законе действующие значения тока и напряжения:

Приборы электромагнитной системы, применяемые для измерений напряжений и токов на переменном токе, регистрируют действующие значения. Соответственно градуируются и шкалы этих приборов

Кривые напряжения и тока в индуктивном сопротивлении

Напряжение на индуктивности определяется выражением

где

-индуктивное сопротивленияе
Индуктивное сопротивление выражают в омах, оно играет роль сопротивления в цепи переменного тока с катушкой индуктивности.
В идеальной индуктивности ток отстает от напряжения на 90°.

Если напряжение на емкости меняется по закону синуса

, то

-емкостное сопротивление.
Емкостное сопротивление выражается в омах, оно играет роль сопротивления в цепи переменного тока с конденсатором.
Кривые напряжения и тока в емкостном сопротивлении
В идеальной емкости ток опережает напряжение на 90°

Режим — состояние электрической цепи переменного тока описывается дифференциальными уравнениями, представляющими собой уравнения с постоянными коэффициентами и правой частью, например:

Из курса высшей математики известно, что общее решение такого уравнения может быть найдено методом наложения принужденного и свободного режимов:

где

— ток принужденного режима при di/dt=0
— ток свободного режима.
Свободные процессы исследуются с целью определения устойчивости системы. В устойчивой системе процессы должны затухать. Принужденный и свободный режимы в сумме определяют процессы, которые называются переходными, т.е. осуществляется переход от одного установившегося режима к другому.
При установившемся режиме ток и напряжение сохраняют в течение длительного времени амплитудные значения.
В цепях постоянного тока токи и напряжения остаются неизменными, а в цепях переменного тока остаются неизменными кривые изменения токов и напряжений.

Мощность цепи переменного тока

В периодическом синусоидальном режиме

Используя известное тригонометрическое преобразование

и обозначив

, получим

Среднее за период значение гармонической функции удвоенной частоты равно нулю.
Измерение мгновенного значения мощности переменного тока затруднено из-за сравнительно большой частоты колебаний (v = 50 Гц). Поэтому на практике принято пользоваться средней мощностью тока. Средняя мощность — это отношение энергии, потребляемой за один период, к периоду:

где

— энергетическое значение коэффициента мощности,

Потребляемая на участке цепи с резистором средняя мощность получила название активной мощности. Она необратимо преобразуется в джоулеву теплоту и другие виды энергии. Мощность, потребляемую на участках цепи с емкостным и индуктивным сопротивлениями, называют реактивной мощностью.
При передаче электрической энергии по цепи переменного тока ее необратимые преобразования происходят только на тех участках цепи, которые содержат резисторы. Такие участки цепи называют активной нагрузкой. На активной нагрузке электроэнергия превращается в теплоту или механическую работу.
Участок цепи с индуктивностью или емкостью называют реактивной нагрузкой. На участках цепи, которые состоят из чистых емкостных или индуктивных сопротивлений, электроэнергия не потребляется. В цепи с реактивными нагрузками происходит только перекачка энергии от генератора к нагрузке и обратно с неизбежными потерями в подводящих проводах.

 

При заданных Р и U ток является функцией cosj. Потери мощности на сопротивлении

В цепи с резистором j=0.

Коэффициент мощности cosj показывает, какая часть полной мощности, вырабатываемой генератором и передаваемой нагрузке, необратимо используется нагрузкой. Он играет важную роль в электротехнике. В самом деле, если в цепи имеется значительный сдвиг по фазе между колебаниями тока и э. д. с, то коэффициент мощности мал и нагрузка потребляет от генератора малую активную мощность. Вместе с тем генератор должен вырабатывать полную мощность S. Эту же мощность должен отдавать генератору первичный двигатель. Таким образом, при низком коэффициенте мощности нагрузка потребляет лишь часть энергии, которую вырабатывает генератор. Оставшаяся часть энергии перекачивается периодически от генератора к потребителю и обратно и рассеивается в линиях электропередачи.
Максимально благоприятные условия передачи электроэнергии создаются в цепи, работающей в режиме резонанса. В самом деле, при приближении к резонансу амплитуда силы тока оказывается максимальной и коэффициент мощности стремится к единице. В этом случае активная мощность приближается к полной мощности, т. е. достигает максимума.
Повышение к. м. является важной народнохозяйственной задачей, от решения которой зависит эффективность использования вырабатываемой электроэнергии.
Уменьшение к. м. в промышленных цепях происходит в основном за счет содержащихся в них трансформаторов и асинхронных электродвигателей, имеющих значительные индуктивные сопротивления. Поэтому повысить к. м. при таких нагрузках можно путем подключения параллельно основной цепи компенсирующих конденсаторов, позволяющих приблизиться к режиму резонанса токов.
С целью повышения к. м. и экономии электроэнергии не следует допускать холостого хода (т. е. работы без нагрузки) трансформаторов и асинхронных электродвигателей, ибо в этом случае они представляют собой чисто индуктивные сопротивления и вызывают дополнительные потери мощности.
Коэффициент мощности (к. м.) ни в коем случае нельзя путать с коэффициентом полезного действия (к. п. д.). Так, например, при определенном соотношении емкости и индуктивности коэффициент мощности в данной цепи может оказаться равным единице. Коэффициент же полезного действия цепи всегда меньше единицы.

Мощность цепи переменного тока

 

Мощность в активном сопротивлении

Мгновенное значение мощности для цепи с резистором:

Из рисунка видно, что потребляемая резистором мгновенная мощность остается все время положительной, но пульсирует с удвоенной по отношению к силе тока и э. д. с. частотой.

Действующее значение мощности:

Активная мощность в цепи с идеальной катушкой индуктивности и конденсатором равна 0. Реактивная мощность определяется выражением:

Аналогично можно проделать для цепи с идеальным конденсатором:

В произвольной цепи переменного тока потребляемая одновременно активной и реактивной нагрузками суммарная мощность

Но так как

, следовательно, . Мы приходим к выводу, что суммарная средняя мощность, потребляемая полной цепью переменного тока, равна активной мощности.

где S — полная мощность, вырабатываемая генератором переменного тока, ВА;
a — сдвиг по фазе между колебаниями э. д. с. и силы тока.

 

Резистивные цепи переменного тока

Однонаправленная величина, будь то напряжение или ток, известна как величина постоянного или постоянного тока, которая имеет постоянную величину во времени, поэтому ее также называют неизменной во времени величиной. С другой стороны, переменная величина является величиной, изменяющейся во времени, поскольку величина и полярность периодически меняются через равные промежутки времени.

[adsense1]

Синусоидальная величина, например напряжение, может быть выражена как V = Vm sin (ωt + θ)

Где

В = мгновенное значение напряжения

Вм = максимальное значение напряжения

ω = угловая скорость = 2π f

θ = фазовый угол

Основными элементами цепи переменного тока являются сопротивление, индуктивность и емкость . В цепях переменного тока используется комбинация этих элементов (любых двух или трех) в последовательных и параллельных комбинациях.

Работа каждой отдельной цепи с отдельными элементами отличается от работы цепи, состоящей из комбинации этих элементов. В этой статье мы собираемся обсудить поведение цепи переменного тока с резистивной нагрузкой.

[adsense2]

Схема

Переменный ток, подаваемый через чистый резистор

В этом случае чистое сопротивление подключается к источнику переменного тока, что эквивалентно схеме, которая подает переменный ток на резистор, лампу или нагреватель или любую другую резистивную нагрузку. Это простейший тип цепи переменного тока, в которой нет ни индуктивности, ни емкости.

Эта чисто резистивная цепь ведет себя как цепь постоянного тока, предлагая такой же тип противодействия переменному току, как и в случае постоянного тока. На рисунке ниже показана резистивная цепь переменного тока с осциллограммами напряжения и тока.

Когда на резистивную нагрузку подается переменное напряжение, ток в цепи зависит от приложенного напряжения, и это значение тока можно определить с помощью закона Ома. Эта величина тока зависит от действующих значений приложенного напряжения и сопротивления в цепи.

Пусть мгновенное значение напряжения v = Vm sin ωt

Тогда ток в цепи по закону Ома определяется как

i = V/R = Vm sin ωt / R

При ωt = 90 ⁰ значение i равно Im, следовательно, Im= Vm/R

Таким образом, ток может быть записан как , i = Im sin ωt

Следовательно, и напряжение, и ток имеют синусоидальную форму а также имеют одинаковую частоту. Это означает, что направление тока изменяется таким же образом, как и приложенное напряжение, и, следовательно, они находятся в фазе друг с другом.

Таким образом, кривые напряжения и тока достигают своих максимальных и минимальных значений в одно и то же время. Однако амплитуды этих сигналов отличаются друг от друга.

Ниже показано векторное представление резистивной цепи переменного тока, в которой сигналы тока и напряжения совпадают по фазе.

Мощность и коэффициент мощности

Мощность в резистивной цепи является произведением напряжения и тока. Средняя мощность в резистивной цепи переменного тока может быть рассчитана как

Поскольку нет разности фаз между сигналами напряжения и тока, фазовый угол равен нулю (θ = 0), и, следовательно, коэффициент мощности будет равен единице.

Коэффициент мощности, cos θ = cos 0 ⁰ = 1

Пример 1

Если в цепи есть источник переменного напряжения 280 В и нагревательный элемент 40 Ом, каков эффективный ток, потребляемый от источника? А также определить мощность, потребляемую нагревательным элементом.

Ток, потребляемый от источника питания,

I = V/R

= 280/40

= 7 ампер

Активная мощность, потребляемая сопротивлением переменного тока, равна

P = i2 R = 42 × 60 = 960 Вт

Пример 1 для резистивной цепи переменного тока

Если переменное синусоидальное напряжение V (t) = 200 x cos (ωt + 60 ⁰ ) подключено к сопротивлению 40 Ом, то какой ток протекает через схема?

Преобразование данного выражения напряжения из временной области в векторную область. Мы получаем VR (t) = 200 cos (ωt + 60 ⁰ ) → VR = 200 ∠60 ⁰ вольт

Применяя закон Ома, ток в цепи можно рассчитать как

IR = VR / R = 200 ♂ 60 ⁰

= 200 ♂ 60 ⁰ /40

= 5om 60 ⁰ AMPS

Схема переменного тока с резистивными нагрузками

На рисунке показано на рисунке. простая цепь переменного тока, состоящая из последовательно соединенных резисторов поперек источника питания. Ток через каждый элемент или в любой точке цепи имеет одинаковое значение из-за последовательного соединения, а его величина зависит от приложенного напряжения и общего сопротивления в цепи.

Независимо от количества последовательно соединенных резисторов ток всегда совпадает по фазе с приложенным напряжением.

В приведенной выше схеме напряжение на каждом сопротивлении можно определить, применяя закон Ома. Сумма падений напряжения на каждом сопротивлении дает общее напряжение, приложенное к цепи.

Соотношение фаз между приложенным напряжением и током этой цепи показано на диаграмме ниже, где как отдельные падения напряжения, так и общее напряжение совпадают по фазе с током.

Пример

Предположим, если в цепи имеется источник переменного напряжения 280 В и два нагревательных элемента соответственно 40 Ом и 60 Ом, то каково падение напряжения на каждом нагревательном элементе.

Полное сопротивление в цепи, Ом _Тл = R1 + R2

= 40 + 60 = 100 Ом 280/ 100 = 2,8 А

Следовательно, I _T = IR1 = IR2

Тогда Падение напряжения на нагревательном элементе-1, V1 = I _T R1 = 2,8 × 40 = 112 В

Падение напряжения на нагревательном элементе-2, V2 = I _T R2 = 2,8 × 60 = 168 В

Параллельная цепь переменного тока с резистивными нагрузками

В параллельной цепи переменного тока различные резистивные нагрузки подключены к источнику переменного напряжения, поэтому напряжение на каждой ветви остается постоянным, а общий ток распределяется между отдельными резистивными ветвями.

Таким образом, общий ток можно определить, сложив все отдельные токи, протекающие через каждое сопротивление. Эти отдельные токи находятся в фазе с приложенным напряжением, поскольку цепь состоит из чисто резистивной нагрузки.

На приведенном выше рисунке показано синфазное соотношение между напряжением и отдельными токами в параллельной цепи переменного тока с чисто резистивной нагрузкой. Величина отдельного тока через резистор зависит от приложенного напряжения и сопротивления, предлагаемого этим резистором.

Чем больше номинал резистора, тем меньше ток через него, и наоборот. Однако эти токи следуют форме волны напряжения (т. Е. В фазе с ней) независимо от их величины.

Пример

Если в цепи есть источник переменного напряжения 240 В, подключенный к двум параллельным нагревательным элементам 390 Ом и 1 кОм соответственно, то каков эффективный ток, протекающий через каждый из нагревательных элементов?

В параллельной цепи напряжение на каждом резисторе одинаковое, т. е. V = V1 = V2

По закону Ома ток через ТЭН-1,

IR1 = V1 / R1 = 240/390 = 0,615 = 615 мА

Аналогично, IR2 = V2 / R2 = 240/1000 = 0,24 = 240 мА

Поэтому токи через нагревательные элементы составляют 615 мА и 240 мА соответственно.

Резистивная цепь переменного тока | Анализ

Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.

В этом руководстве рассматривается анализ резистивной цепи переменного тока, а также несколько решенных примеров для расчета полного сопротивления, тока и мощности в цепи переменного тока.

Когда переменное напряжение подается на цепь, оно вызывает протекание по цепи переменного тока той же частоты. Для чисто резистивных цепей переменного тока напряжение и ток находятся в фазе друг с другом, как показано на рисунке 1 .

Напряжение и ток считаются совпадающими по фазе, поскольку две формы волны проходят через свои нулевые значения и одновременно увеличиваются в одном направлении до своих максимальных значений.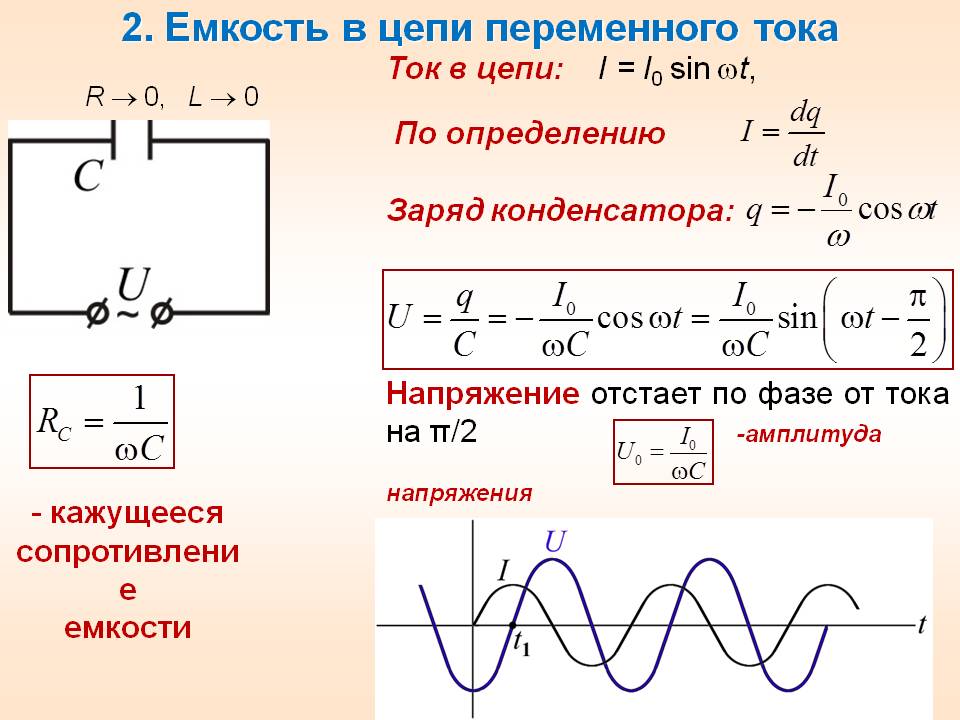 Следовательно, разность фаз между волнами, находящимися в фазе, равна нулю.

Рисунок 1  Аналоговое напряжение резистивной цепи переменного тока и кривые тока.

По большей части чисто резистивные цепи реагируют практически одинаково на цепи переменного или постоянного тока. Резистивные нагревательные элементы и лампы накаливания считаются чисто резистивными нагрузками. Резистивные нагрузки характеризуются тем, что они выделяют тепло , а ток и напряжение находятся в фазе друг с другом.

Теоретически ни одна цепь переменного тока не может содержать только сопротивление. Другие свойства могут влиять на напряжение и ток в гораздо меньшей степени, что позволяет рассматривать цепь как чисто резистивную.

В общем, все законы и формулы, применимые к цепям постоянного тока, применимы и к цепям переменного тока. Кроме того, они применяют точно так же, как , к резистивным цепям переменного тока. Это верно, потому что резисторы являются линейными компонентами и их характеристики не зависят от частоты.

В резистивной цепи постоянного тока и ток, и напряжение имеют фиксированные устойчивые значения. В резистивной цепи переменного тока ток изменяется точно в соответствии с напряжением. Формула закона Ома для цепи переменного тока может быть выражен как

Если не указано иное, все значения напряжения и тока переменного тока приведены как эффективные или среднеквадратичные значения . Имея это в виду, формула закона Ома для цепи переменного тока также может быть выражена как

При вычислении величин в резистивных цепях переменного тока важно помнить, что значения переменного тока не смешиваются. При поиске эффективных значений все значения, которые вы используете в формуле, должны быть эффективными значениями. Точно так же, когда вы решаете для пиковых или средних значений, все используемые вами значения должны быть пиковыми или средними значениями.

Общее сопротивление в резистивной схеме ACE Пример 1

Проблема: Схема последовательности состоит из трех резисторов ( R ₁ = 6 ω, R ₂ = 4 ω, R ₂ = 4 Ω, 7777777777777777777 гг. ₃  = 5 Ом) и источник переменного напряжения 120 вольт, как показано на рис. 2 . Определить полное сопротивление цепи и действующее значение протекающего тока.

Рисунок 2  Активная резистивная цепь переменного тока, например 1.

Решение:

В цепи постоянного тока мощность равна произведению напряжения на силу тока ( P = E × I ) . Это также верно в цепи переменного тока, когда ток и напряжение совпадают по фазе; то есть, когда цепь является резистивной. При переменном токе значения тока и напряжения меняются со временем. В любой момент мощность равна силе тока в этот момент, умноженной на напряжение в этот момент.

График всех мгновенных мощностей, как показано на  Рисунок 3 , формирует сигнал мощности. Обратите внимание, что форма волны мощности всегда  90 189 положительная 90 190  для синфазных токов и напряжений. Отрицательный ток, умноженный на отрицательное напряжение, дает положительную мощность. Это означает, что резистивная нагрузка преобразует электрическую энергию в тепловую в течение всего цикла. Тогда мощность, рассеиваемая на чисто резистивной нагрузке, питаемой от источника переменного тока, равна 90 189 и равна 90 190  , что и для резистора, подключенного к источнику постоянного тока, и определяется как

Рисунок 3  Мощность в резистивной цепи переменного тока.

Где I и E — эффективные или среднеквадратичные значения тока и напряжения.

Полная мощность в резистивной цепи переменного тока Пример 2

Задача:  Найти эффективную общую мощность, потребляемую однофазной резистивной цепью  Рисунок 4 .

Рис. 4 Резистивная цепь переменного тока для примера 2.

Решение:

Для трехфазных резистивных цепей напряжения и токи обычно выражаются в виде среднеквадратичных или эффективных значений, как при анализе однофазных цепей. Мощность в ваттах, подаваемая на трехфазную сбалансированную резистивную нагрузку, рассчитывается следующим образом:

Мощность резистивного контура, пример 3

Задача: . Найдите эффективную общую мощность, потребляемую сбалансированной трехфазной резистивной нагревательной нагрузкой. схема Рисунок 5 .

Решение:

обычно проще измерить линейное напряжение и ток в трехфазной системе.

Однако в трехфазной симметричной резистивной системе полная мощность цепи также равна сумме мощностей каждой из трех фаз или трехкратной мощности одной фазы:

На рисунке 6 показано подключение одного ваттметра , используемого для измерения трехфазной мощности сбалансированной трехфазной резистивной нагрузки. Обратите внимание, что ваттметр подключается для измерения фазного тока и напряжения. Соответственно, трехкратное измеренное значение ваттметра равно трехфазной мощности, пока три фазы сбалансированы.

Рисунок 6  Одиночный ваттметр, используемый для измерения трехфазной мощности.

Два ваттметра можно использовать для измерения трехфазной мощности в системах, содержащих только трехфазные проводники, путем измерения линейного тока и напряжения. На рисунке 7 показано подключение для так называемого двухваттметра  метода измерения мощности в трехфазных системах.

Если трехфазная система симметричная и резистивная, то показания двух ваттметров будут одинаковыми, а общая мощность цепи будет равна сумме показаний двух ваттметров Вт ₁  и W ₂ . Важно соблюдать полярность ( ±) на катушках напряжения и тока ваттметров и выполнять соединения точно так, как показано.

Рисунок 7 Двухваттметровый метод измерения трехфазной мощности.

Вопросы для повторения

1. Каково фазовое соотношение между напряжением и током в резистивной цепи переменного тока?
2. Во что все резистивные нагрузки преобразуют электроэнергию?
3. Переменное напряжение 340 В от пика к пику подключено к нагревателю на 10 Ом. Определите:
   1. Пиковое значение напряжения.
   2. Действующее значение напряжения.
   3. Мощность обогревателя.
4. Последовательная цепь состоит из двух резисторов сопротивлением 4 Ом, подключенных к источнику постоянного напряжения 24 вольта.
   1. Определите общее сопротивление и протекающий ток.
   2. Повторите для той же цепи, подключенной к источнику переменного тока 24 В.
5. Нагреватель печи на 240 В переменного тока состоит из четырех нагревательных элементов сопротивлением 20 Ом, соединенных параллельно. Определите номинальную мощность агрегата в кВт.
6. Линейное напряжение и ток, подаваемые на сбалансированную трехфазную резистивную группу нагрузки, соединенную звездой, измеряются и составляют 415 вольт и 30 ампер соответственно.
   1. Каково значение напряжения на одной фазе блока нагрузки?
   2. Каково значение тока через одну фазу блока нагрузки?
   3. Каково значение общей мощности в кВт, подаваемой на блок нагрузки?
   4. Если подключить один ваттметр для измерения напряжения и тока любой фазы, каковы будут его показания в кВт?
7. Линейное напряжение и ток, подаваемые на сбалансированную трехфазную резистивную группу нагрузки, соединенную треугольником, измеряются и составляют 480 вольт и 104 ампера соответственно.
   1. Каково значение общей мощности в кВт, подаваемой на блок нагрузки?
   2. Если используется метод измерения мощности с двумя ваттметрами, какое значение в кВт будет W ₁ и W ₂ быть?
8. Сравните напряжения четырехпроводной системы 208, соединенной звездой, с напряжением четырехпроводной системы 480, соединенной звездой.
9. Для цепи переменного тока Рисунок 8  определить все значения напряжения, тока, сопротивления и мощности. Запишите свои ответы в виде таблицы.

Рисунок 8  Схема для контрольного вопроса 9.

     

Обзор Вопросы – ответы

1. Эти два вопроса находятся в фазе друг с другом.
2. Они выделяют тепло.
3. (а) 170 В, (б) 120 В, (в) 1440 Вт
4. (а) R _T = 8 Ом, I _T = 3 А, (б) R _T = 8 Ом , I _T = 3 A
5. R _T = 5 Ом, P _T = 11,52 кВт
6. (a) 240 В, (b) 30 A, (c) 21,6 кВт, (d) 7,2 кВт
7. (а) P _T = 86,6 кВт, (б) Вт ₁ = Вт ₂ = 43.2 kW
8. 208 V and 120 V or 480 V and 277 V

	Voltage	Current	Resistance	Power
R 1	80 V	8 A	10 Ω	640 W
R 2	40 V	4 A	10 Ω	160 W
R 3	40 V	4 A	10 Ω	160 W
TOTAL	120 V	8 A	15 Ω	960 W

10.