Содержание
Экспонента комплексного числа
|
|
|
||||||||||||||||||||||||||||||
Угол между ними.
Матрица смежности онлайн
Формула Эйлера, том II — aj tz’ihb — LiveJournal
Завершаем обсуждение формулы Эйлера
Продолжая рассуждения предыдущей части, в итоге получаем степенной ряд (он же ряд Маклорена, он же ряд Тейлора) для экспоненты
который прекрасно сходится и ничуть не страдает, если вещественную переменную х заменить в нем на комплексную z:
Вообще, по нынешним временам, именно этот ряд нередко берут как определение экспоненты, а ее остальные свойства из него выводятся.
Например, то, что при дифференцировании этот ряд переходит сам в себя, достаточно очевидно, по-моему.
Обратите внимание, насколько простая идея стоит за кулисами ряда Тейлора. Если положить
То автоматически
благодаря тому, что слева от k-го члена слагаемые обнулятся дифференцированием, а справа за счет ненулевой степени разности. И вуаля:
Но да, нюанс. Это все конечно весело и приятно, но сходимость полученных рядов следует исследовать отдельно, тут целое поле граблей, по которым математики 18 века вдоволь находились. И здесь как раз вступают в бой все те признаки и свойства сходимости, почленной дифференцируемости и т.п. из курса матанализа. Но мы этим здесь заниматься не будем, а будем верить мне на слово.
Еще одно замечание по дороге. Если мы определяем экспоненту в виде ряда, то совершенно необязательно в этот ряд подставлять числа. Если для некоторых сущностей определены операции сложения, умножения между собой и умножения на число, а так же осмысленно понятие предела, то есть задана банахова алгебра, то ряд для экспоненты имеет вполне себе внятный смысл.
Например, можно взять экспоненту от квадратной матрицы. А то и еще чего почище учудить. Но это уже другая история.
Возвращаясь к формуле Эйлера, я уже без вывода, прямо запишу:
И, чтоб упростить вам восприятие:
Ряды у нас хорошие, складывать их можно как угодно. И на данном этапе формула
представляется совершенно очевидной. Видимо Эйлер именно так к ней и пришел: играясь с рядами Маклорена.
Если пойти еще немгого дальше, то вообще окажется, что синус и косинус удобнее определить следующим образом:
а дальнейшие нужные нам свойства тригонометрических функций доказать.
Кстати, обратите внимание, что выражение
имеет период два пи вдоль мнимой оси. Так что, помимо известных свойств, у экспоненты появились и некоторые новые. Представить заранее, что экспонента станет периодической функцией, было бы (наверное) довольно сложно.
Напоследок скажу, что хотя формула Муавра уже была известна к моменту открытия Эйлера, возможность представить любое комплексное число в виде открыла совершенно новые, невиданные возможности. В качестве простого и очень примитивного примера, чтобы не быть голословным, напомню, что именно на этом представлении базируются всем известные методы расчета линейных цепей переменного тока. Есть и куда более интересные применения, но о них как-нибудь в другой раз.
Tags: opus, математика
комплексный анализ — Можно ли вычислять тригонометрические функции с мнимой экспонентой
Задавать вопрос
спросил
Изменено
5 лет, 10 месяцев назад
Просмотрено
9{-i \тета}}{2}$.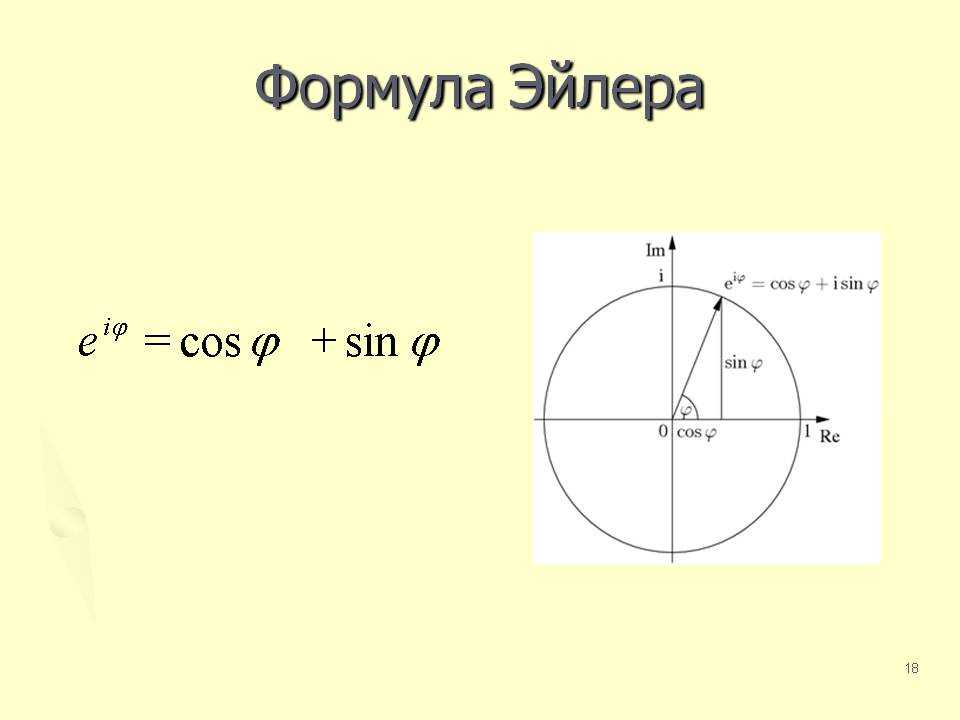
Не могли бы вы по этим формулам рассчитать конкретные значения тригонометрической функции? Я предполагаю, что комплексная экспонента может быть рассчитана только с использованием тождества Эйлера, поэтому для начала вам нужно знать значения синуса/косинуса. Есть ли способ вычислить значение синуса/косинуса, используя приведенное выше тождество? Есть ли причина, по которой это невозможно (возможно?)?
- комплексный анализ
- тригонометрия
- комплексные числа
9{-i\theta}$$
По сути, все, что вы можете сделать в декартовых координатах, можно сделать и в комплексной плоскости, и часто намного проще (на мой взгляд).
$\endgroup$
$\begingroup$
Технически, вы можете использовать ряд Маклорена экспоненциальной функции для вычисления синуса и косинуса при любом значении $\theta$, которое вы хотите. Но вы обнаружите, что когда вы упростите получившиеся выражения, они окажутся равными ровно 9п(х)$?
спросил
Изменено
Просмотрено
$\begingroup$
Когда тригонометрическая функция имеет показатель степени, означает ли это, что она умножает сама себя или рекурсивно применяется к результату? Например, обозначает ли $\sin(x)^2$ $\sin(x)\sin(x)$ или $\sin(\sin(x))$? А как насчет $\sin^2x$? 92 обычно (в зависимости от языка) означает «вычислить функцию Фибоначчи с вводом $4$, а затем возвести результат в квадрат».
25 дней назад
7к раз
Добавить комментарий