Величины токов протекающих через два последовательно соединенных проводника: Последовательное и параллельное соединение проводников

Содержание

Последовательное и параллельное соединение проводников – изучение формул

4.7

Средняя оценка: 4.7

Всего получено оценок: 221.

4.7

Средняя оценка: 4.7

Всего получено оценок: 221.

Электрические схемы представляют собой набор различных электронных компонент, с помощью которых получают (или преобразовывают) постоянные и переменные электрические сигналы нужной величины, формы и частоты. Для этого элементы схемы соединяют в определенном порядке. Самыми распространенными типами соединений являются последовательное и параллельное соединение проводников.

Закон Ома

Изучение последовательного и параллельного соединения проводников следует начинать с напоминания закона Ома, который является базовым законом при проектировании всех видов электрических схем.

Немецкий физик Георг Ом в 1826 г. экспериментально открыл фундаментальную связь между силой тока I и напряжением U. Ученый установил, что величина тока I в цепи прямо пропорциональна величине напряжения U, т. е. I ∼ U.

Рис. 1. Закон Ома

Формула закона Ома для однородного участка цепи выглядит следующим образом:

$ I = {U \over R} $ (1),

где: R — величина сопротивления проводника, (Ом).

Полностью закон Ома звучит так: сила тока I для проводника на однородном участке цепи прямо пропорциональна напряжению U на этом участке и обратно пропорциональна сопротивлению проводника R.

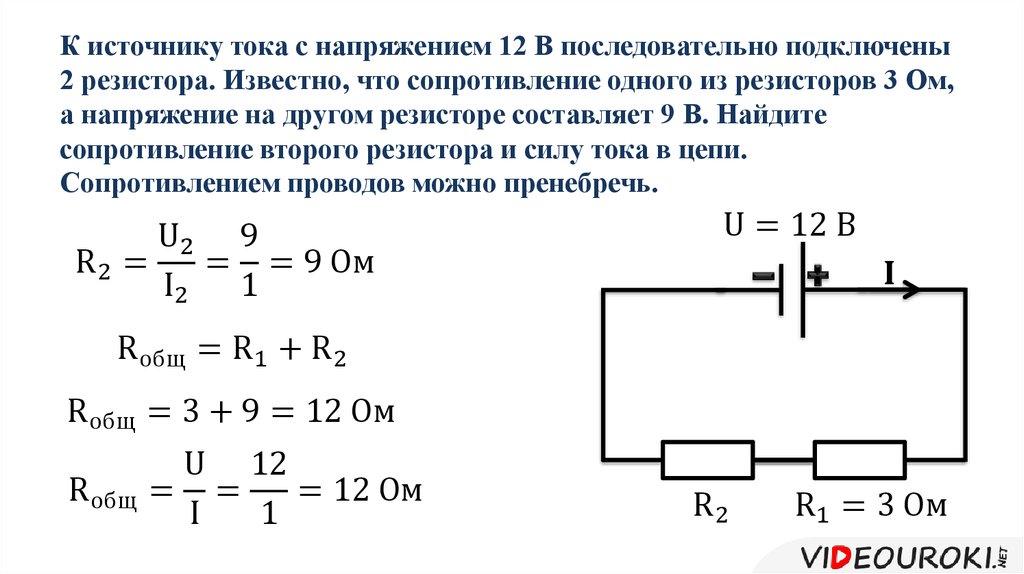
Последовательное соединение проводников

Для простоты будем рассматривать соединения проводников на примере резисторов (сопротивлений) R. Если взять два резистора R₁ и R₂и соединить их друг за другом (правый контакт резистора R₁с левым контактом резистора R₂, то это будет последовательное соединение.

Рис. 2. Схема последовательного соединения резисторов

При подключении напряжения U к левому концу R₁и правому концу R₂ в замкнутой цепи потечет ток I, величина которого будет одинакова для обоих резисторов. Падение напряжений U₁ и U₂ на сопротивлениях согласно закону Ома будут равны:

$ U_1 = I * R_1 $$ (2), $$ U_2 = I * R_2 $ (3).

Полное напряжение U равно сумме этих напряжений:

$ U = U_1 + U_2 $ (4).

Применив закон Ома для всей цепи, получим:

$ U = I * R_{общ} $ (5),

где R_общ — общее сопротивление всей цепи. Из формул (2), (3) и (4) следует, что:

$ U = I * R = I * R_1 + I * R_2 $ (6).

Сократив обе части уравнения на I, получим:

$ R_{общ} =R_1 + R_2 $ (7).

Если в цепи последовательно соединены N резисторов — R_1,R_2… R_N, то, воспользовавшись такими же соображениями, можно получить формулу для величины общего сопротивления такой цепи R₀:

$$ R_0 = R_1 + R_2 +…+ R_N $$ (8).

Таким образом, можно сформулировать общее правило: при последовательном соединении резисторов величина общего сопротивления цепи равна сумме сопротивлений включенных резисторов.

Параллельное соединение проводников

Если взять два резистора R₁ и R₂и соединить их так, что начала (левые концы) соединятся в одной точке, а правые концы соединятся в другой точке, то это и будет параллельное соединение.

Рис. 3. Схема параллельного соединения резисторов

После подключения к левому и правому концам источника напряжения U, в цепи потечет ток. Поскольку R₁ и R₂ могут отличаться друг от друга, то и значения токов I₁ и I₂ через них тоже будут разные. Зная напряжение U, и используя формулу закона Ома, можно рассчитать токи I₁ и I₂ :

$ I_1 = {U \over R_1} $ (9),

$ I_2 = {U \over R_2} $ (10)

Общий ток I в цепи является суммой токов I₁ и I₂:

$ I = I_1 + I_2 $ (11),

Тогда, используя выражения для токов I₁ и I₂, получим следующую формулу:

${U \over R} = { U \over R_1}+ {U \over R_2}$ (12).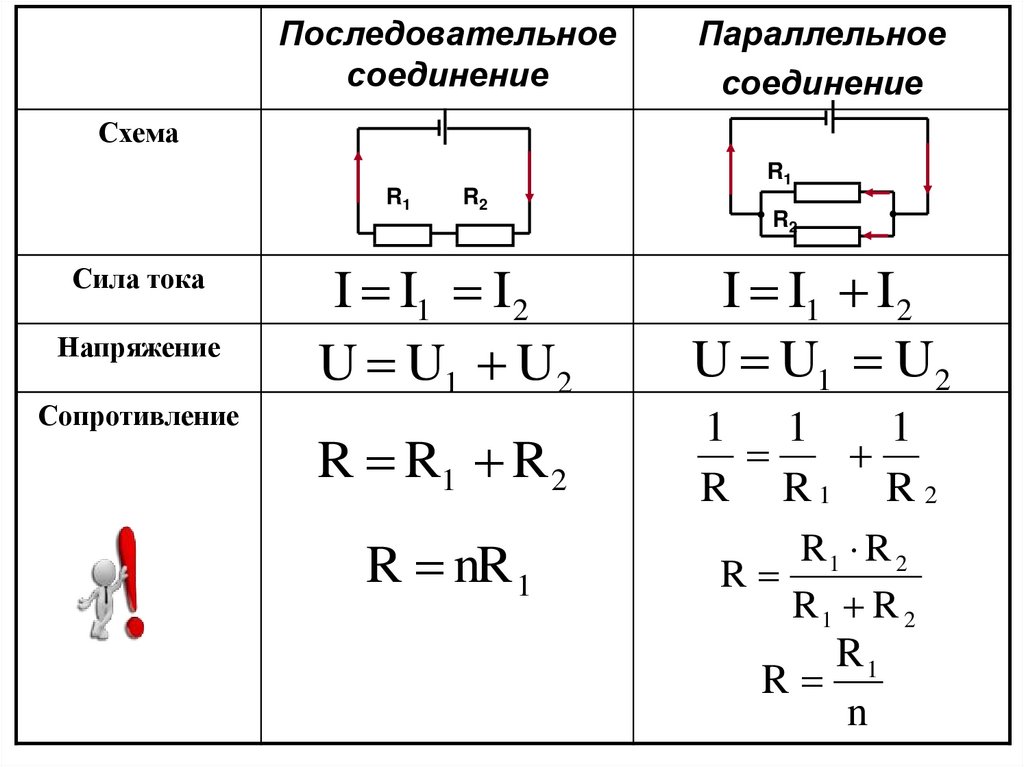

Сокращая обе части последнего уравнения на U, получим следующее выражение для обратной величины общего сопротивления R:

$ {1\over R} = {1 \over R_1}+ {1 \over R_2} $ (13).

Используя последнюю формулу и правило сложения дробей, получим выражение для сопротивления цепи, состоящей из двух резисторов:

$ R = {R_1* R_2 \over R_1 + R_2} $ (14).

Если соединить параллельно N резисторов с одинаковым сопротивлением R₀, то общее сопротивление цепи будет равно:

$ R = {R_0 \over N} $.

Что мы узнали?

Итак, мы узнали, что такое последовательное и параллельное соединение проводников в электрических цепях. Получены формулы для вычисления общих сопротивлений цепей при последовательном и параллельном соединениях.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 221.

А какая ваша оценка?

Глава 21. Электрический ток. Законы Ома и Джоуля-Ленца

Для решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.

Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени

(21.1)

Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.

Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то

(21.2)

Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.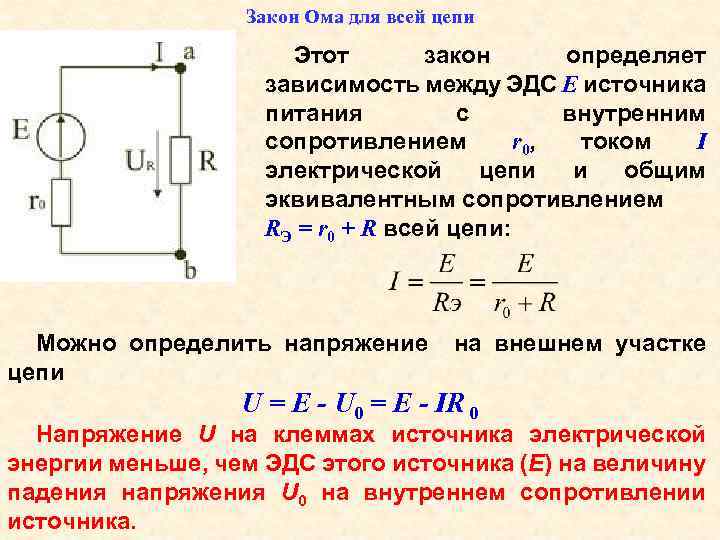 2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид

(21.3)

Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).

Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения

(21.4)

где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.

Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников

(21. 4)

Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников

(21.5)

Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду

(21. 6)

В этом случае сила тока в цепи равна

(21.7)

Формула (21.7) называется законом Ома для замкнутой электрической цепи.

При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно

(21.8)

(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение

(21. 9)

которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.

Рассмотрим теперь задачи.

Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).

Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.1.2)

(ответ 2).

Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).

По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.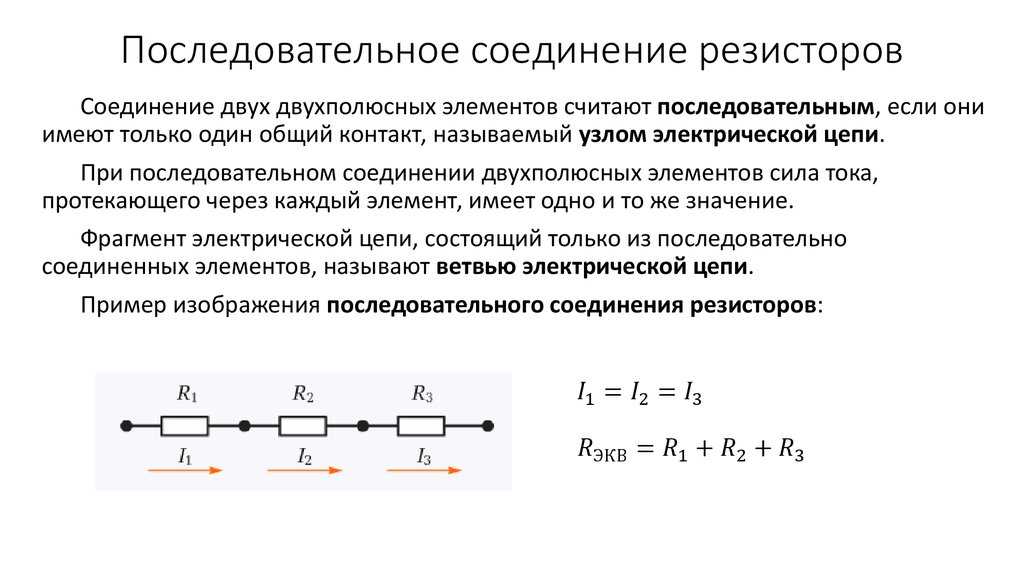 1.4)

Таким образом, сила тока уменьшилась в 4 раза (ответ 3).

Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика

(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.

Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6

где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем

(ответ 3).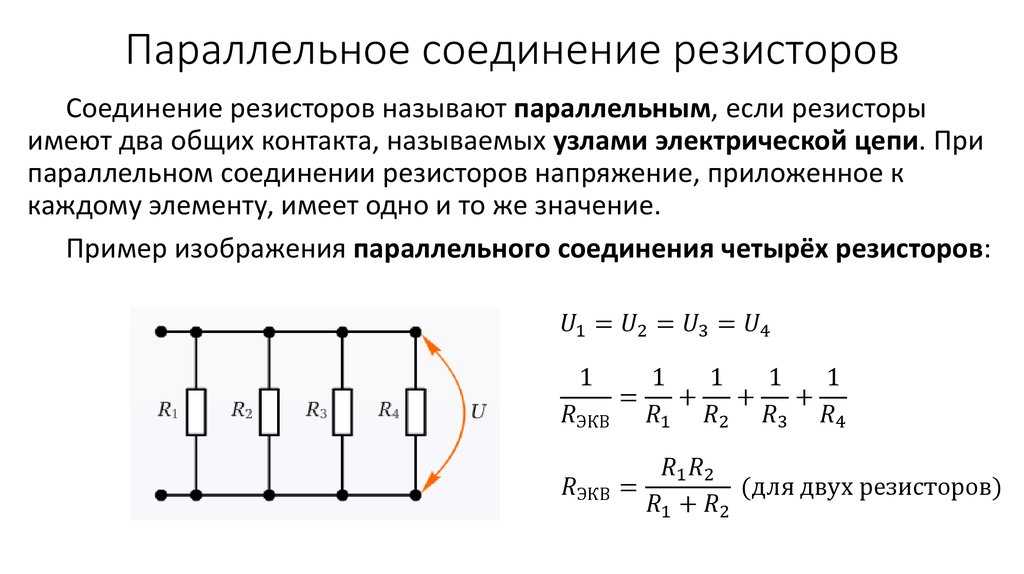

Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).

В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем

где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).

В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому

где — внутреннее сопротивление источника (ответ 3).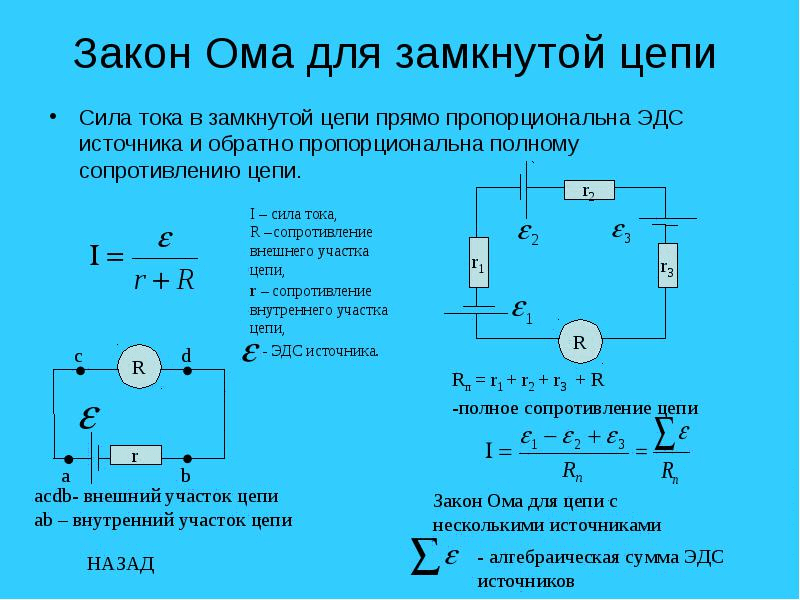

Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).

В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).

Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.

Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.

Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно

(ответ 2).

Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что

(ответ 2).

При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что

(ответ 1).

Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка

а затем и эквивалентное сопротивление всей цепи

(ответ 3).

При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).

Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна

где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:

(ответ 2).

Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —

(ответ 1).

Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22. 8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца

где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).

Учебное пособие по физике: последовательные цепи

Как упоминалось в предыдущем разделе урока 4, два или более электрических устройства в цепи могут быть соединены последовательно или параллельно. Когда все устройства соединены с помощью последовательных соединений, цепь называется последовательной цепью . В последовательной цепи каждое устройство подключено таким образом, что существует только один путь, по которому заряд может пройти через внешнюю цепь. Каждый заряд, проходящий через петлю внешней цепи, будет последовательно проходить через каждый резистор.

В предыдущем разделе урока 4 было проведено краткое сравнение и противопоставление последовательной и параллельной цепей. В этом разделе было подчеркнуто, что добавление большего количества резисторов в последовательную цепь приводит к довольно ожидаемому результату в виде увеличения общей сопротивление. Поскольку в цепи есть только один путь, каждый заряд сталкивается с сопротивлением каждого устройства; поэтому добавление большего количества устройств приводит к увеличению общего сопротивления. Это повышенное сопротивление служит для уменьшения скорости протекания заряда (также известной как ток).

Эквивалентное сопротивление и ток

Заряды текут вместе по внешней цепи со скоростью, которая везде одинакова. Ток в одном месте не больше, чем в другом. Фактическая величина тока обратно пропорциональна величине общего сопротивления. Существует четкая зависимость между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Что касается батареи, которая качает заряд, наличие двух 6-омных резисторов, соединенных последовательно, будет эквивалентно наличию в цепи одного 12-омного резистора. Наличие трех последовательно соединенных резисторов сопротивлением 6 Ом будет эквивалентно наличию в цепи одного резистора сопротивлением 18 Ом. А наличие четырех резисторов на 6 Ом последовательно было бы эквивалентно наличию в цепи одного резистора на 24 Ом.

Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи представляет собой величину сопротивления, которая потребуется одному резистору, чтобы уравнять общий эффект набора резисторов, присутствующих в цепи. Для последовательных цепей математическая формула для расчета эквивалентного сопротивления (R _экв.) выглядит следующим образом:

R _экв. = R ₁ + R ₂ + R ₃ + …

, где R ₁ , R ₂ и R ₃ — значения сопротивления отдельных резисторов, соединенных последовательно.

Больше практики

Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже. Составьте себе задачу с любым количеством резисторов и любых номиналов. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Ток в последовательной цепи везде одинаков. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах. Заряд НЕ расходуется резисторами так, что в одном месте его меньше, чем в другом. Заряды можно представить себе как марширующие вместе по проводам электрической цепи, везде марширующие с одинаковой скоростью. Ток — скорость, с которой течет заряд, — везде одинакова. Это то же самое на первом резисторе, что и на последнем резисторе, как и в батарее. Математически можно написать

I _{батарея} = I ₁ = I ₂ = I ₃ = …

где I 902 902 2 1 9002 23 , а I ₃ — текущий значения в отдельных местах резисторов.

Эти значения тока легко рассчитать, если известно напряжение батареи и известны значения отдельных сопротивлений. Используя значения отдельных резисторов и приведенное выше уравнение, можно рассчитать эквивалентное сопротивление. А используя закон Ома (ΔV = I • R), можно определить ток в батарее и, следовательно, через каждый резистор, найдя соотношение напряжения батареи и эквивалентного сопротивления.

I _{батарея} = I ₁ = I ₂ = I ₃ = ΔV _{батарея} / R

3

3 2

Разность электрических потенциалов и падение напряжения
Как обсуждалось в Уроке 1, электрохимическая ячейка цепи подает энергию заряду для его перемещения через ячейку и создания разности электрических потенциалов на двух концах внешней цепи. Ячейка на 1,5 вольта создаст разность электрических потенциалов во внешней цепи 1,5 вольта. Это означает, что электрический потенциал на положительной клемме на 1,5 вольт больше, чем на отрицательной клемме. Когда заряд движется по внешней цепи, он теряет 1,5 вольта электрического потенциала. Эта потеря электрического потенциала называется падение напряжения . Это происходит, когда электрическая энергия заряда преобразуется в другие формы энергии (тепловую, световую, механическую и т. д.) внутри резисторов или нагрузок. Если электрическая цепь, питаемая от 1,5-вольтовой ячейки, оснащена более чем одним резистором, то суммарная потеря электрического потенциала составляет 1,5 вольта. На каждом резисторе есть падение напряжения, но сумма этих падений напряжения составляет 1,5 вольта — столько же, сколько номинальное напряжение источника питания. Эта концепция может быть выражена математически следующим уравнением:

ΔV _{батарея} = ΔV ₁ + ΔV ₂ + ΔV ₃ + . ..

Чтобы проиллюстрировать этот математический принцип в действии, рассмотрим две схемы, показанные ниже на диаграммах A и B. что вас попросили определить два неизвестных значения разности электрических потенциалов между лампочками в каждой цепи. Чтобы определить их значения, вам придется использовать приведенное выше уравнение. Батарея изображается своим обычным схематическим символом, а ее напряжение указывается рядом с ним. Определите падение напряжения для двух лампочек, а затем нажмите кнопку «Проверить ответы», чтобы убедиться, что вы правы.

Ранее в Уроке 1 обсуждалось использование диаграммы электрического потенциала. Диаграмма электрических потенциалов — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим принципиальную схему ниже и соответствующую ей диаграмму электрических потенциалов.

Схема, показанная на схеме выше, питается от 12-вольтового источника питания.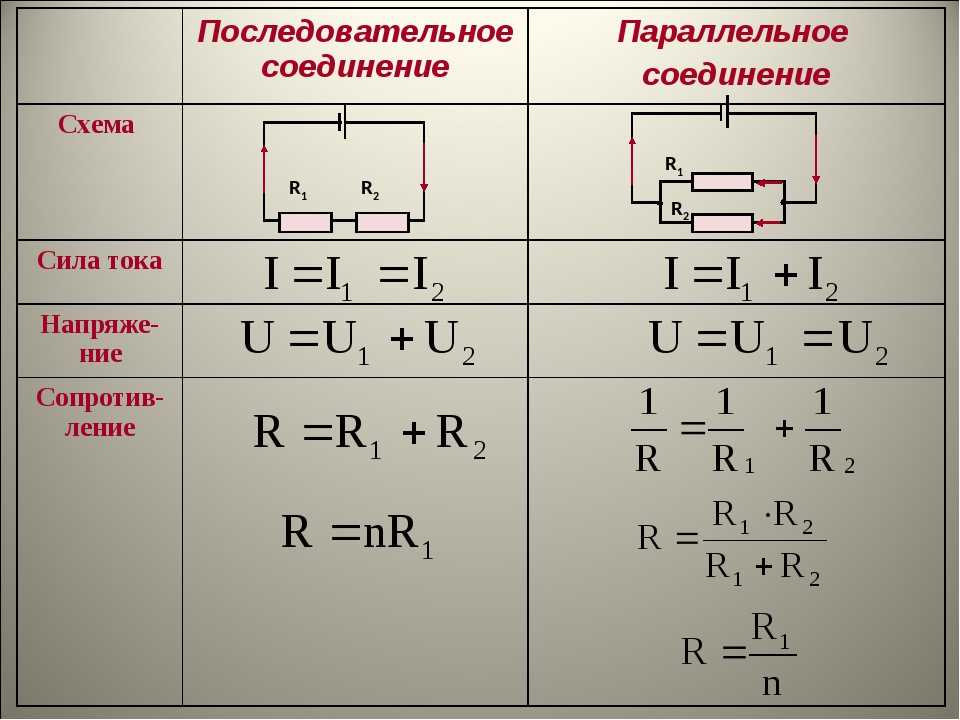 В цепи последовательно соединены три резистора, каждый из которых имеет свое падение напряжения. Отрицательный знак разности электрических потенциалов просто означает, что при прохождении через резистор происходит потеря электрического потенциала. Обычный ток направляется по внешней цепи от положительного вывода к отрицательному. Поскольку схематический символ источника напряжения использует длинную полосу для обозначения положительной клеммы, место А на схеме соответствует положительной клемме или клемме с высоким потенциалом. Место A находится под напряжением 12 вольт, а место H (отрицательная клемма) находится под напряжением 0 вольт. Проходя через аккумулятор, заряд приобретает 12 вольт электрического потенциала. А при прохождении через внешнюю цепь заряд теряет 12 вольт электрического потенциала, как показано на диаграмме электрических потенциалов, показанной справа от принципиальной схемы. Эти 12 вольт электрического потенциала теряются за три этапа, каждый из которых соответствует протеканию через резистор. При прохождении через соединительные провода между резисторами происходит небольшая потеря электрического потенциала из-за того, что провод оказывает относительно небольшое сопротивление потоку заряда. Поскольку точки А и В разделены проводом, они имеют практически одинаковый электрический потенциал 12 В. Когда заряд проходит через его первый резистор, он теряет 3 В электрического потенциала и падает до 9 В.V в точке C. Поскольку точка D отделена от точки C простым проводом, она имеет фактически тот же электрический потенциал 9 В, что и C. Когда заряд проходит через второй резистор, он теряет 7 В электрического потенциала и падает вниз. до 2 В в точке E. Поскольку точка F отделена от точки E простым проводом, она имеет фактически тот же электрический потенциал 2 В, что и E. Наконец, когда заряд проходит через последний резистор, он теряет 2 В электрического тока. потенциала и падает до 0 В в точке G. В точках G и H заряду не хватает энергии, и ему требуется повышение энергии, чтобы снова пройти через внешнюю цепь. Повышение энергии обеспечивается аккумулятором по мере того, как заряд перемещается от H к A.

В уроке 3 закон Ома (ΔV = I • R) был представлен как уравнение, связывающее падение напряжения на резисторе с сопротивлением резистора и током на резисторе. Уравнение закона Ома можно использовать для любого отдельного резистора в последовательной цепи. При объединении закона Ома с некоторыми принципами, уже обсуждавшимися на этой странице, возникает большая идея.

В последовательных цепях резистор с наибольшим сопротивлением имеет наибольшее падение напряжения.

Поскольку ток в последовательной цепи везде одинаков, значение I ΔV = I • R одинаково для каждого из резисторов последовательной цепи. Таким образом, падение напряжения (ΔV) зависит от изменения сопротивления. Везде, где сопротивление наибольшее, падение напряжения будет наибольшим на этом резисторе. Уравнение закона Ома можно использовать не только для прогнозирования того, что резистор в последовательной цепи будет иметь наибольшее падение напряжения, но и для расчета фактических значений падения напряжения.

Δ В ₁ = I • R ₁ Δ В ₂ = I • R ₂ Δ В ₃ = I • R ₃

Математический анализ последовательных цепей
Приведенные выше принципы и формулы можно использовать для анализа последовательной цепи и определения значений тока при и разности электрических потенциалов на каждом из резисторов в последовательной цепи. Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R _eq), тока в батарее (I _tot), а также падения напряжения и тока для каждого из трех резисторов.

Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.

R _eq = R ₁ + R ₂ + R ₃ = 17 Ом + 12 Ом + 11 Ом = 40 Ом

Теперь, когда известно эквивалентное сопротивление батареи можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в цепи важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R. Расчет показан здесь:

I _tot = ΔV _{батареи} / R _eq = (60 В) / (40 Ом) = 1,5 ампера

Значение тока 1,5 ампера — это ток в месте расположения батареи. Для последовательной цепи без мест разветвления ток везде одинаков. Ток в месте расположения батареи такой же, как ток в каждом месте резистора. Следовательно, 1,5 ампера — это значение I ₁ , I ₂ и I ₃ .

I _{аккумулятор} = I ₁ = I ₂ = I ₃ = 1,5 А

Осталось определить три значения — падение напряжения на каждом из отдельных резисторов. Закон Ома снова используется для определения падения напряжения на каждом резисторе — это просто произведение тока на каждом резисторе (рассчитанного выше как 1,5 ампера) и сопротивления каждого резистора (указанного в условии задачи). Расчеты показаны ниже.

ΔV ₁ = I ₁ • R ₁

ΔV ₁ = (1,5 А) • (17 Ом)

ΔV ₁ = 25,5 В

ΔV ₂ = I ₂ • R ₂

ΔV ₂ = (1,5 А) • (12 Ом)

ΔV ₂ = 18 В

ΔV ₃ = I ₃ • R ₃

ΔV ₃ = (1,5 А) • (11 Ом)

ΔV ₃ = 16,5 В

В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли рассчитанные значения принципу, согласно которому сумма падений напряжения на каждом отдельном резисторе равна номинальному напряжению батареи. Другими словами, является ли ΔV _{батарея} = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Является ли батарея ΔV = ΔV ₁ + ΔV ₂ + ΔV ₃ ?

Является ли 60 В = 25,5 В + 18 В + 16,5 В?

Является ли 60 В = 60 В?

Да!!

Математический анализ этой последовательной цепи включал сочетание концепций и уравнений. Как это часто бывает в физике, отрыв понятий от уравнений при решении физической задачи — опасный поступок. Здесь необходимо учитывать понятия, что ток везде одинаков и что напряжение батареи эквивалентно сумме падений напряжения на каждом резисторе, чтобы завершить математический анализ. В следующей части урока 4 параллельные цепи будут проанализированы с использованием закона Ома и концепций параллельных цепей. Мы увидим, что подход смешивания понятий с уравнениями будет столь же важен для этого анализа.

Мы хотели бы предложить . ..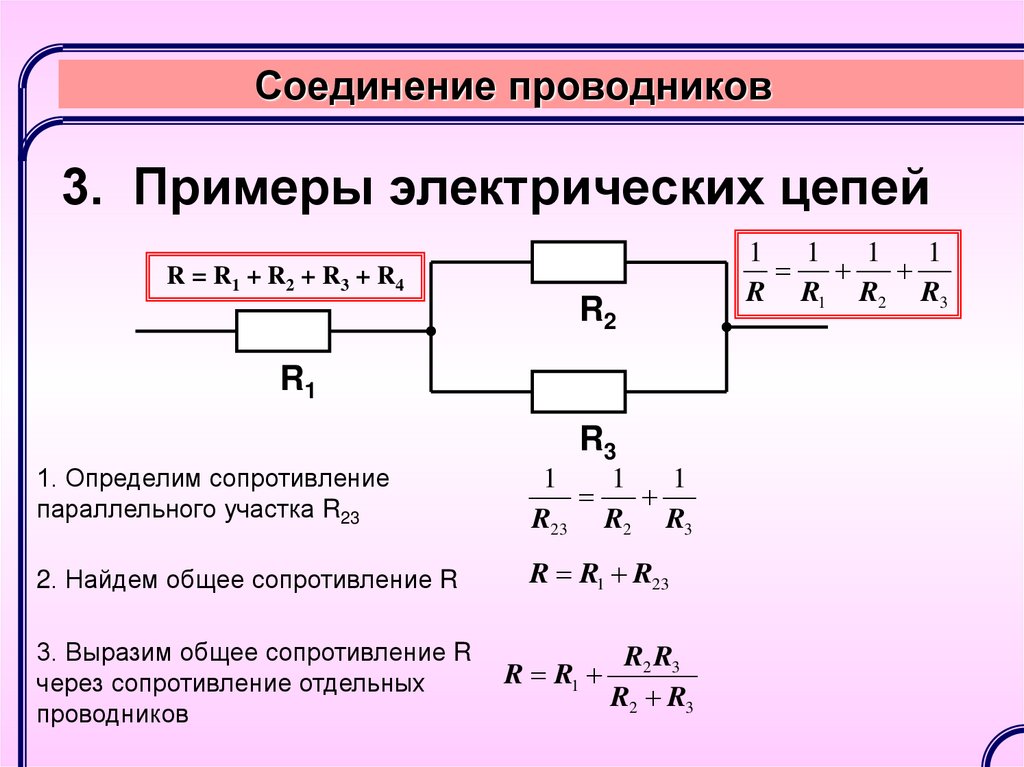
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Вы можете легко перетаскивать источники напряжения, резисторы и провода на рабочее место, располагать и соединять их так, как пожелаете. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Прикосновение к резистору или источнику напряжения позволяет изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если только вы не используете его в ванной).

Посетите: DC Circuit Builder

Проверьте свое понимание

1. Используйте свое понимание эквивалентного сопротивления, чтобы завершить следующие утверждения:

a. Два последовательно соединенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное одному резистору сопротивлением _____ Ом.

б. Три последовательно соединенных резистора сопротивлением 3 Ом обеспечат сопротивление, эквивалентное одному резистору сопротивлением _____ Ом.

с. Три последовательно соединенных резистора сопротивлением 5 Ом обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

д. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

эл. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

ф. Три резистора с сопротивлением 12 Ом, 3 Ом и 21 Ом включены последовательно. Они обеспечат сопротивление, эквивалентное одному резистору _____-Ом.

2. При увеличении количества резисторов в последовательной цепи общее сопротивление __________ (увеличивается, уменьшается, остается неизменным) и ток в цепи __________ (увеличивается, уменьшается, остается неизменным).

3. Рассмотрим следующие две схемы последовательных цепей. Для каждой диаграммы используйте стрелки, чтобы указать направление условного тока. Затем сравните напряжение и ток в обозначенных точках для каждой диаграммы.

4. Три одинаковые лампочки подключены к D-ячейке, как показано справа. Какое из следующих утверждений верно?

а. Все три лампочки будут иметь одинаковую яркость.

б. Лампочка между X и Y будет самой яркой.

в. Лампочка между Y и Z будет самой яркой.

д. Лампочка между Z и батареей будет самой яркой.

5. Три одинаковые лампочки подключены к батарейке, как показано справа. Какие корректировки можно внести в схему, чтобы увеличить ток, измеряемый в точке X? Перечислите все, что применимо.

а. Увеличьте сопротивление одной из лампочек.

б. Увеличьте сопротивление двух лампочек.

в. Уменьшите сопротивление двух лампочек.

д. Увеличьте напряжение батареи.

эл. Уменьшите напряжение батареи.

ф. Снимите одну из лампочек.

6. Три одинаковые лампочки подключены к батарейке, как показано справа. W, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?

а. Разность потенциалов между X и Y больше, чем между Y и Z.

б. Разность потенциалов между X и Y больше, чем между Y и W.

в. Разность потенциалов между Y и Z больше, чем между Y и W.

д. Разность потенциалов между X и Z больше, чем между Z и W.

эл. Разность потенциалов между X и W больше, чем на аккумуляторе.

ф. Разность потенциалов между X и Y больше, чем между Z и W.

7. Сравните схемы X и Y ниже. Каждый питается от 12-вольтовой батареи. Падение напряжения на резисторе 12 Ом в цепи Y равно ____ падению напряжения на одном резисторе в цепи X.

a. меньше чем

б. больше

в. то же, что

8. Батарея 12 В, резистор 12 Ом и лампочка подключены, как показано на схеме X ниже. Резистор на 6 Ом добавляется к резистору на 12 Ом и лампочке, чтобы создать цепь Y, как показано на рисунке. Лампочка появится ____.

а. диммер в контуре X

б. диммер в цепи Y

в. одинаковая яркость в обоих контурах

9. Три резистора соединены последовательно.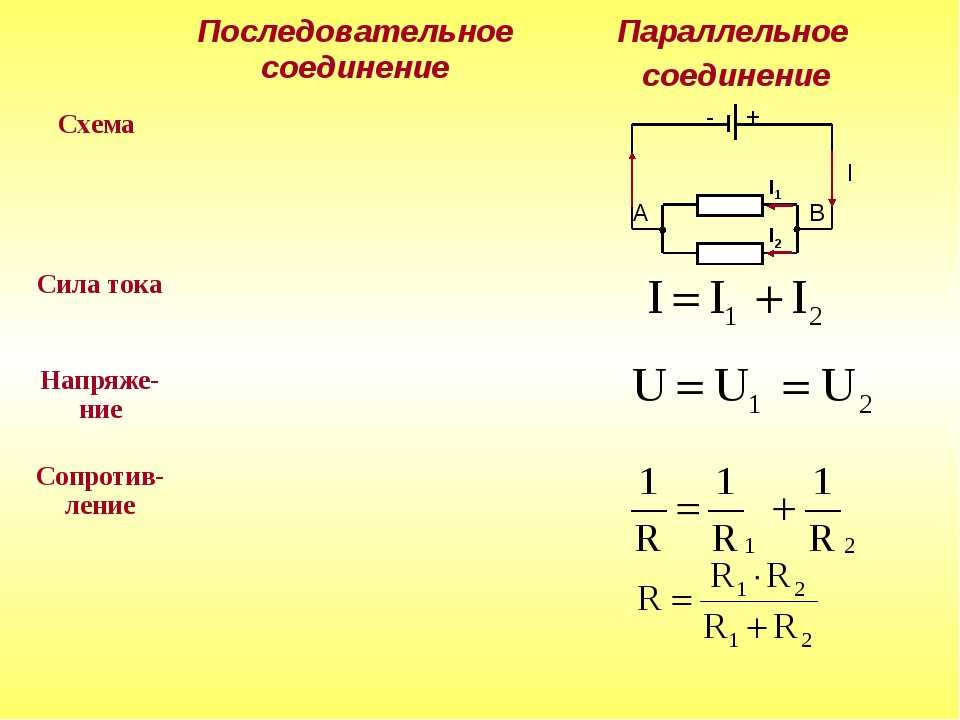 Если поместить в цепь с 12-вольтовым источником питания. Определить эквивалентное сопротивление, общий ток цепи, падение напряжения и ток на каждом резисторе.

Следующий раздел:

20.1 Текущая – Колледж Физика

Резюме

Определение электрического тока, силы тока и скорости дрейфа

Опишите направление потока заряда в обычном токе.

Используйте скорость дрейфа для расчета тока и наоборот.

Электрический ток определяется как скорость, с которой течет заряд. Большой ток, например, используемый для запуска двигателя грузовика, перемещает большое количество заряда за короткое время, в то время как слабый ток, например, используемый для работы ручного калькулятора, перемещает небольшое количество заряда в течение короткого времени. длительный период времени. В форме уравнения электрический ток [латекс]\boldsymbol{I}[/латекс] определяется как

[латекс]\boldsymbol{I =}[/латекс] [латекс]\boldsymbol{\frac{\Delta Q}{\Delta t}}[/latex]

, где [латекс]\boldsymbol{\Delta Q}[/латекс] — количество заряда, проходящего через данную область за время [латекс]\boldsymbol{\Delta t}[/латекс].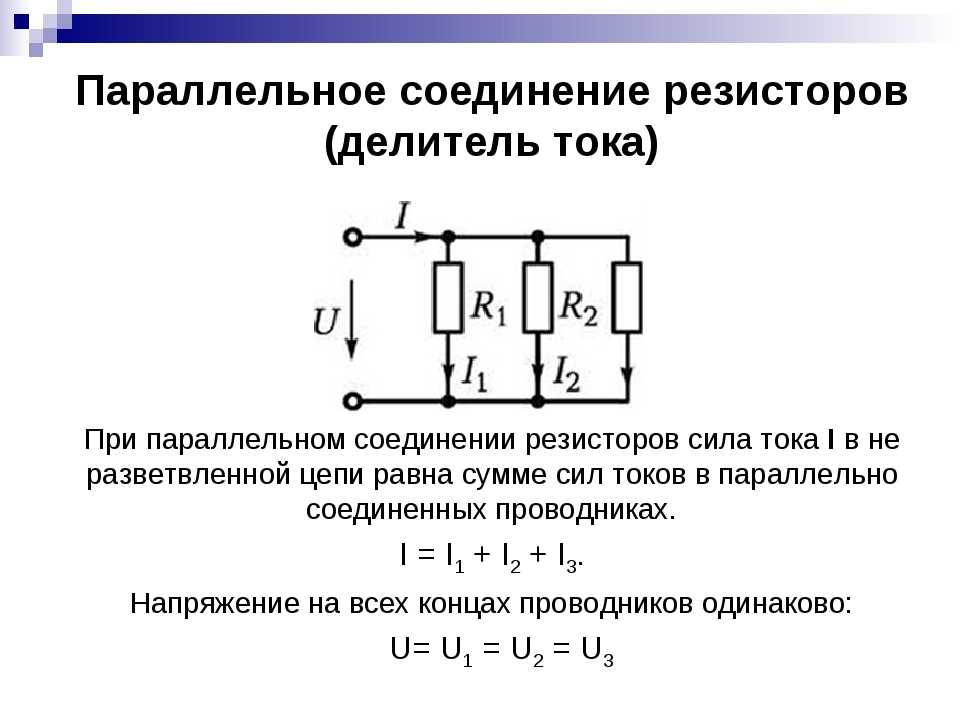 (Как и в предыдущих главах, начальное время часто принимается равным нулю, и в этом случае [латекс]\жирныйсимвол{\Delta t = t}[/латекс].) (См. рис. 1.) Единицей СИ для тока является ампера (А), названный в честь французского физика Андре-Мари Ампера (1775–1836). Поскольку [latex]\boldsymbol{I = \Delta Q / \Delta t}[/latex], мы видим, что ампер равен одному кулону в секунду:

[латекс]\boldsymbol{1 \;\textbf{A} = 1 \;\textbf{C} / \textbf{s}}[/latex]

В амперах (или амперах) указаны не только предохранители и автоматические выключатели, но и многие электроприборы.

Рисунок 1. Скорость потока заряда текущая. Ампер — это поток в один кулон через площадь за одну секунду.

Пример 1: Расчет токов: ток в аккумуляторе грузовика и портативном калькуляторе

(a) Какой ток возникает, когда аккумулятор грузовика приводится в движение с зарядом 720 Кл за 4,00 с при запуске двигателя? б) Сколько времени потребуется заряду 1,00 Кл, чтобы пройти через карманный калькулятор, если через него протекает ток 0,300 мА?

Стратегия

Мы можем использовать определение тока в уравнении [латекс]\boldsymbol{I = \Delta Q / \Delta t}[/латекс], чтобы найти ток в части (а), так как заряд и время дается.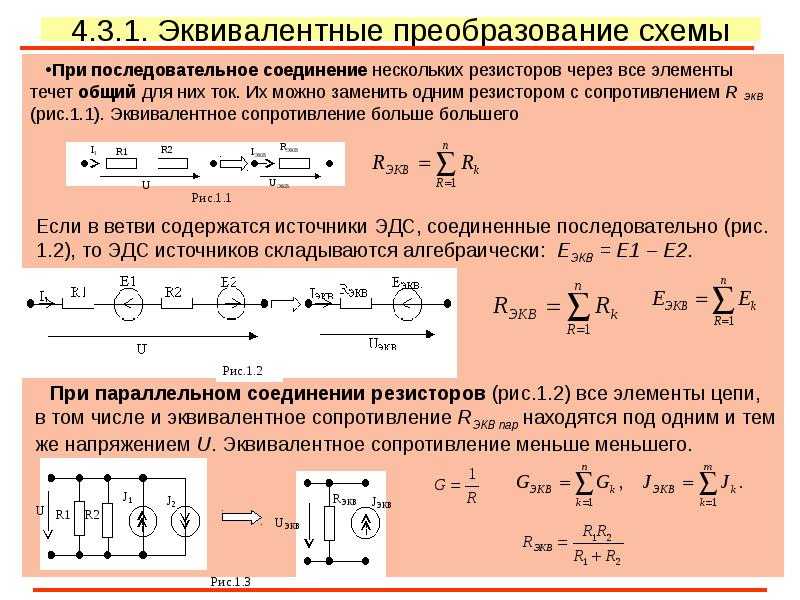 В части (b) мы меняем определение тока и используем заданные значения заряда и тока, чтобы найти требуемое время.

Решение для (a)

Ввод заданных значений заряда и времени в определение тока дает

[латекс]\begin{array}{r @{{}={}} l} \boldsymbol{ I} & \boldsymbol{\frac{\Delta Q}{\Delta t} = \frac{720 \;\textbf{C}}{4,00 \;\textbf{s}} = 180 \;\textbf{C} / \textbf{s}} \\[1em] & \boldsymbol{180 \;\textbf{A}}. \end{array}[/latex]

Обсуждение для (a)

Это большое значение тока иллюстрирует тот факт, что большой заряд перемещается за небольшой промежуток времени. Токи в этих «стартерах» довольно велики, поскольку при приведении чего-либо в движение необходимо преодолевать большие силы трения. 93 \;\textbf{s}}. \end{array}[/latex]

Обсуждение для (b)

Это время чуть меньше часа. Небольшой ток, используемый ручным калькулятором, требует гораздо больше времени для перемещения меньшего заряда, чем большой ток стартера грузовика.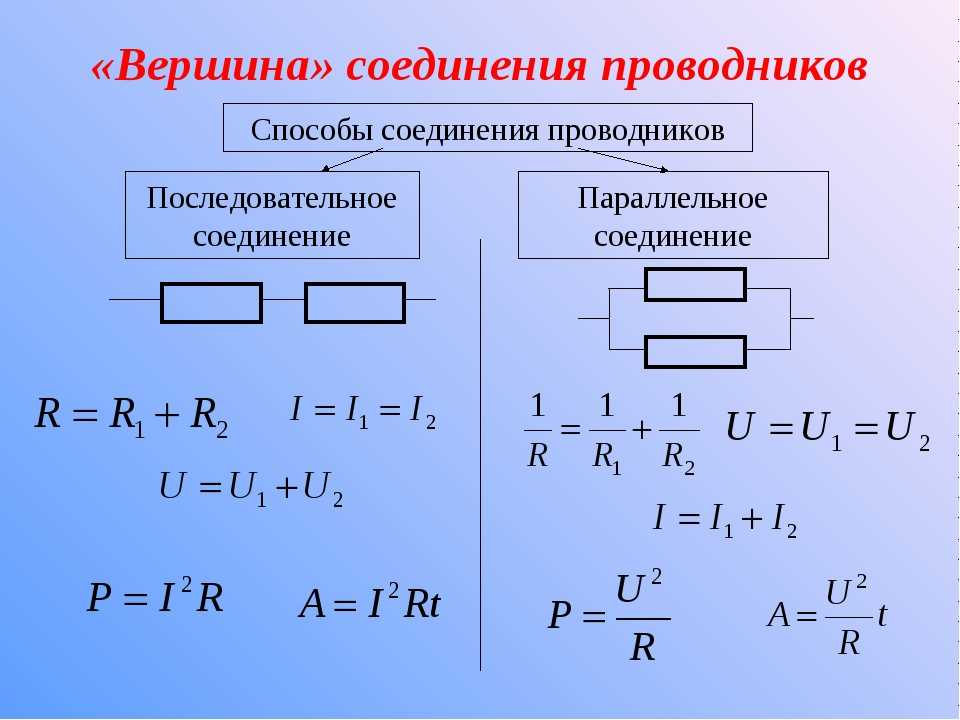 Так почему же мы можем работать с нашими калькуляторами всего через несколько секунд после их включения? Это потому, что калькуляторы требуют очень мало энергии. Такие малые требования к току и энергии позволяют портативным калькуляторам работать от солнечных батарей или работать много часов от небольших батарей. Помните, что в калькуляторах нет движущихся частей, как в двигателе грузовика с цилиндрами и поршнями, поэтому технология требует меньших токов.

На рис. 2 показана простая схема и стандартное схематическое представление батареи, проводящего пути и нагрузки (резистора). Схемы очень полезны для визуализации основных особенностей схемы. Одна схема может отображать множество ситуаций. Схема на рис. 2(b), например, может представлять что угодно: от аккумулятора грузовика, подключенного к фаре, освещающей улицу перед грузовиком, до небольшой батареи, подключенной к фонарику-ручке, освещающему замочную скважину в двери. Такие схемы полезны, потому что анализ одинаков для самых разных ситуаций.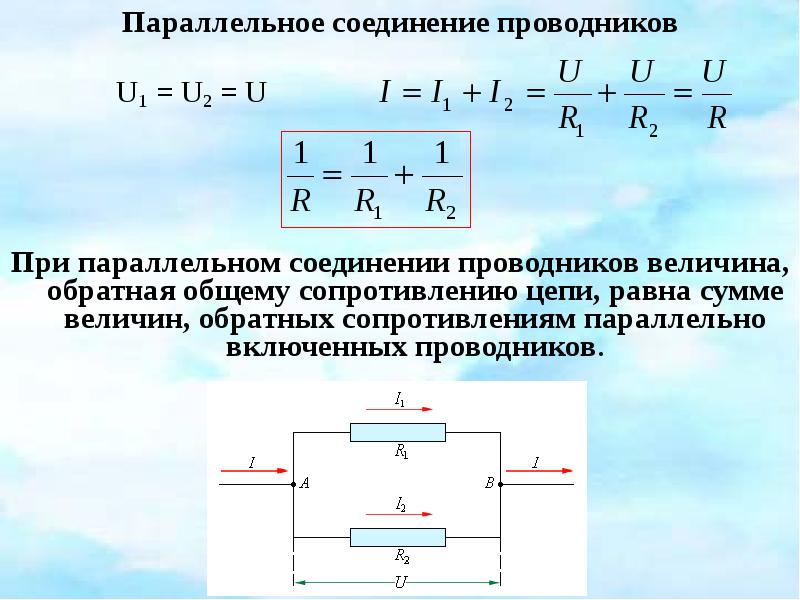 Нам нужно понять несколько схем, чтобы применить концепции и анализ ко многим другим ситуациям.

Рис. 2. (а) Простая электрическая цепь. Замкнутый путь для протекания тока обеспечивается проводящими проводами, соединяющими нагрузку с клеммами батареи. (b) На этой схеме батарея представлена двумя параллельными красными линиями, проводники показаны прямыми линиями, а зигзаг представляет собой нагрузку. Схема представляет большое разнообразие подобных схем.

Обратите внимание, что направление тока на рис. 2 — от положительного к отрицательному. Направление обычного тока — это направление, в котором будет течь положительный заряд . В зависимости от ситуации могут перемещаться положительные заряды, отрицательные заряды или и то, и другое. В металлических проводах, например, ток переносится электронами, то есть движутся отрицательные заряды. В ионных растворах, таких как соленая вода, движутся как положительные, так и отрицательные заряды. Это верно и для нервных клеток. Генератор Ван де Граафа, используемый для ядерных исследований, может производить ток чисто положительных зарядов, таких как протоны. Рисунок 3 иллюстрирует движение заряженных частиц, составляющих ток. Тот факт, что обычный ток считается направленным в сторону положительного заряда, можно проследить до американского политика и ученого Бенджамина Франклина в 1700-х годах. Он назвал тип заряда, связанного с электронами, отрицательным задолго до того, как стало известно, что они несут ток во многих ситуациях. Франклин, по сути, совершенно не знал о мелкомасштабной структуре электричества.

Важно понимать, что в проводниках, ответственных за производство тока, существует электрическое поле, как показано на рисунке 3. В отличие от статического электричества, где проводник, находящийся в равновесии, не может иметь в себе электрического поля, проводники, по которым течет ток, имеют электрическое поле. поле и не находятся в статическом равновесии. Электрическое поле необходимо для подачи энергии для перемещения зарядов.

Установление связей: домашнее исследование — иллюстрация электрического тока

Найдите соломинку и горошины, которые могут свободно перемещаться в соломе. Положите соломинку на стол и наполните ее горошком. Когда вы вставляете одну горошину с одного конца, другая горошина должна выскочить с другого конца. Эта демонстрация представляет собой аналогию электрического тока. Определите, что сравнивается с электронами и что сравнивается с запасом энергии. Какие еще аналогии вы можете найти для электрического тока?

Обратите внимание, что движение гороха основано на физическом столкновении горошин друг с другом; электроны текут за счет взаимно отталкивающих электростатических сил.

Рис. 3. Ток I — это скорость, с которой заряд проходит через площадь A , такую как поперечное сечение провода. Условный ток определен для движения в направлении электрического поля. (а) Положительные заряды движутся в направлении электрического поля и в том же направлении, что и обычный ток. {-19-}{\textbf{s}}} \end{array}[/latex]

Обсуждение

Заряженных частиц, движущихся даже в малых течениях, так много, что отдельные заряды не замечаются, как отдельные воды молекулы не замечаются в потоке воды. Еще более удивительно то, что они не всегда продолжают двигаться вперед, как солдаты на параде. Скорее они похожи на толпу людей с движением в разных направлениях, но общей тенденцией двигаться вперед. В металлической проволоке происходит множество столкновений с атомами и, конечно же, с другими электронами. 9{-4} \;\textbf{m} / \textbf{s}}[/latex]. Как нам согласовать эти две скорости и что это говорит нам о стандартных проводниках?

Высокая скорость электрических сигналов обусловлена тем, что сила между зарядами быстро действует на расстоянии. Таким образом, когда свободный заряд попадает в провод, как на рис. 4, входящий заряд отталкивает другие заряды впереди себя, которые, в свою очередь, отталкивают заряды дальше по линии. Плотность заряда в системе нельзя легко увеличить, поэтому сигнал передается быстро. Возникающая в результате ударная волна электрического тока движется по системе почти со скоростью света. Точнее, этот быстро движущийся сигнал или ударная волна представляет собой быстро распространяющееся изменение электрического поля.0006
Рисунок 4. Когда заряженные частицы попадают в этот объем проводника, такое же количество быстро вынуждено покинуть его. Отталкивание между одноименными зарядами затрудняет увеличение количества зарядов в объеме. Таким образом, как только входит один заряд, другой почти сразу уходит, быстро перенося сигнал вперед.

Хорошие проводники имеют большое количество свободных зарядов. В металлах свободными зарядами являются свободные электроны. На рис. 5 показано, как свободные электроны движутся по обычному проводнику. Расстояние, которое может пройти отдельный электрон между столкновениями с атомами или другими электронами, весьма мало. Таким образом, траектории электронов кажутся почти случайными, как движение атомов в газе. Но в проводнике есть электрическое поле, которое заставляет электроны дрейфовать в указанном направлении (противоположном полю, поскольку они отрицательны).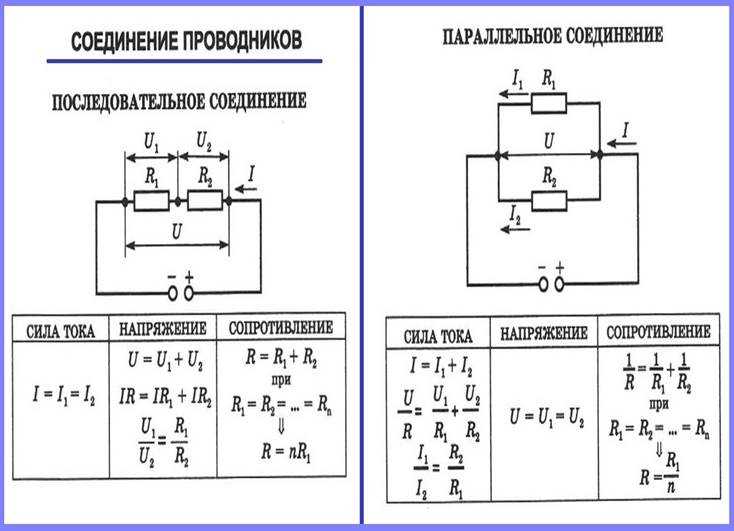 скорость дрейфа [латекс]\boldsymbol{v_d}[/латекс] — средняя скорость свободных зарядов. Скорость дрейфа довольно мала, поскольку так много свободных зарядов. Если у нас есть оценка плотности свободных электронов в проводнике, мы можем рассчитать скорость дрейфа для данного тока. Чем больше плотность, тем ниже скорость, необходимая для данного тока.

Рис. 5. Свободные электроны, движущиеся в проводнике, совершают много столкновений с другими электронами и атомами. Показан путь одного электрона. Средняя скорость свободных зарядов называется скоростью дрейфа v _d , и в направлении, противоположном электрическому полю для электронов. Столкновения обычно передают энергию проводнику, что требует постоянной подачи энергии для поддержания постоянного тока.

Проводимость электричества и тепла

Хорошие электрические проводники часто также являются хорошими проводниками тепла. Это связано с тем, что большое количество свободных электронов может переносить электрический ток и переносить тепловую энергию.

Столкновения свободных электронов передают энергию атомам проводника. Электрическое поле выполняет работу по перемещению электронов на расстояние, но эта работа не увеличивает кинетическую энергию (и, следовательно, скорость) электронов. Работа передается атомам проводника, возможно повышая температуру. Таким образом, для поддержания протекания тока требуется непрерывная потребляемая мощность. Исключение, конечно, составляют сверхпроводники по причинам, которые мы рассмотрим в одной из последующих глав. Сверхпроводники могут иметь постоянный ток без постоянного источника энергии — большая экономия энергии. Напротив, подача энергии может быть полезной, например, в нити накала лампочки. Подача энергии необходима для повышения температуры вольфрамовой нити, чтобы нить накала светилась.

Установление связей: домашнее расследование — Наблюдение за нитью

Найдите лампочку с нитью накаливания. Посмотрите внимательно на нить и опишите ее структуру. К каким точкам присоединяется нить?

Мы можем получить выражение для зависимости между током и скоростью дрейфа, рассмотрев количество свободных зарядов в сегменте проволоки, как показано на рисунке 6. {-19} \;\textbf{C}}[/latex].) Ток – это заряд, перемещаемый в единицу времени; таким образом, если все первоначальные заряды перемещаются из этого сегмента за время [latex]\boldsymbol{\Delta t}[/latex], ток равен

[латекс]\boldsymbol{I =}[/латекс] [латекс]\boldsymbol{\frac{\Delta Q}{\Delta t}}[/латекс] [латекс]\boldsymbol{=}[/латекс] [ латекс] \boldsymbol{\frac{qnAx}{\Delta t}}.[/latex]

Обратите внимание, что [latex]\boldsymbol{x / \Delta t}[/latex] — величина скорости дрейфа, [latex]\boldsymbol{v _{\textbf{d}}}[/latex], поскольку заряды переместиться на среднее расстояние [латекс]\boldsymbol{x}[/латекс] за время [латекс]\boldsymbol{\Delta t}[/латекс]. Перестановка терминов дает

[латекс]\boldsymbol{I = nqAv _{\textbf{d}}}[/латекс],

где [латекс]\boldsymbol{I}[/латекс] — ток через провод с площадью поперечного сечения [латекс]\boldsymbol{А}[/латекс], изготовленный из материала с плотностью свободного заряда [латекс]\ жирныйсимвол{n}[/латекс]. Каждый из носителей тока имеет заряд [латекс]\boldsymbol{q}[/латекс] и движется с дрейфовой скоростью величины [латекс]\жирный символ{v_{\textbf{d}}}[/латекс].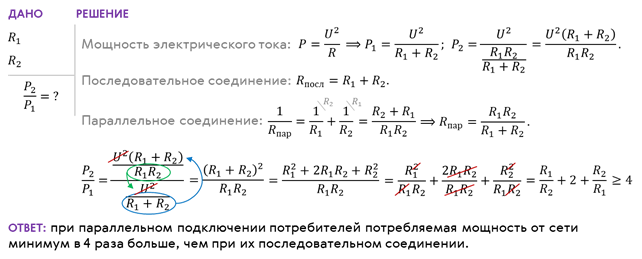

Рис. 6. Все заряды в заштрихованном объеме этой проволоки удаляются за время t , скорость дрейфа которого составляет v _d = x/t . См. текст для дальнейшего обсуждения.

Обратите внимание, что простая скорость дрейфа — это еще не все. Скорость электрона намного больше скорости его дрейфа. Кроме того, не все электроны в проводнике могут двигаться свободно, а те, которые могут двигаться, могут двигаться несколько быстрее или медленнее скорости дрейфа. Так что же мы подразумеваем под свободными электронами? Атомы в металлическом проводнике упакованы в виде решетчатой структуры. Некоторые электроны находятся достаточно далеко от ядер атомов, поэтому они не испытывают притяжения ядер так сильно, как внутренние электроны. Это свободные электроны. Они не связаны ни с одним атомом, а вместо этого могут свободно перемещаться среди атомов в «море» электронов. Эти свободные электроны реагируют ускорением при приложении электрического поля.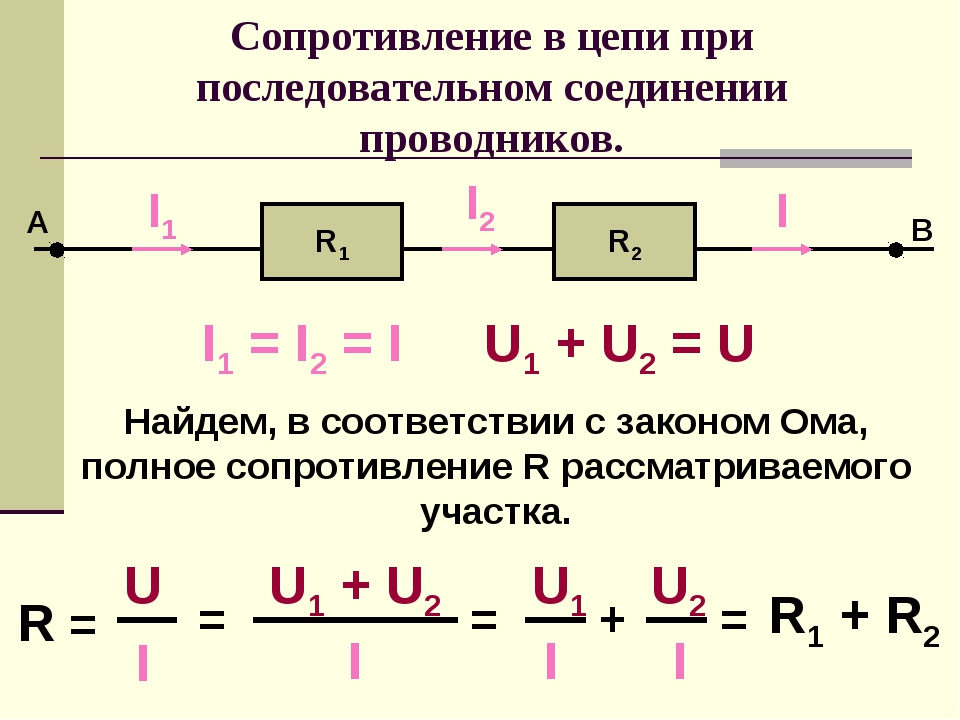 Конечно, когда они движутся, они сталкиваются с атомами в решетке и другими электронами, выделяя тепловую энергию, и проводник нагревается. В изоляторе организация атомов и структура не допускают таких свободных электронов. 98 \;\textbf{m} / \textbf{s}}[/latex]), чем несущие его заряды.

Электрический ток [латекс]\boldsymbol{I}[/латекс] — это скорость, с которой течет заряд, определяемая выражением
[латекс]\boldsymbol{I = \frac{\Delta Q}{\Delta t}},[/latex]

, где [латекс]\boldsymbol{\Delta Q}[/латекс] — количество заряда, проходящего через площадь во времени [латекс]\boldsymbol{\Delta t}[/латекс].

Направление обычного тока принимается за направление, в котором движется положительный заряд. 905:30
Единицей силы тока в системе СИ является ампер (А), где [latex]\boldsymbol{1 \;\textbf{A} = 1 \;\textbf{C} / \textbf{s}}[/latex].

Ток — это поток свободных зарядов, таких как электроны и ионы.

Скорость дрейфа [латекс]\boldsymbol{v_{\textbf{d}}}[/латекс] — средняя скорость, с которой движутся эти заряды.

Текущий [латекс]\boldsymbol{I}[/latex] пропорционален скорости дрейфа [латекс]\boldsymbol{v_{\textbf{d}}}[/латекс], выраженной в соотношении [латекс]\boldsymbol{ I = nqAv _{\textbf{d}}}[/латекс]. Здесь [латекс]\boldsymbol{I}[/латекс] — ток через провод с площадью поперечного сечения [латекс]\жирный символ{А}[/латекс]. Материал проволоки имеет плотность свободного заряда [латекс]\boldsymbol{n}[/латекс], а каждый носитель имеет заряд [латекс]\boldsymbol{q}[/латекс] и дрейфовую скорость [латекс]\boldsymbol{v_ {\textbf{d}}}[/латекс]. 9{12}}[/latex] раз больше дрейфовой скорости свободных электронов.

Задачи и упражнения

1: Какова сила тока в миллиамперах, создаваемая солнечными элементами карманного калькулятора, через который проходит заряд 4,00 Кл за 4,00 ч?

2: Всего через фонарь проходит заряд 600 Кл за 0,500 ч. Какой средний ток?

3: Какова сила тока, когда типичный статический заряд [латекс]\boldsymbol{0,250 \;\mu \textbf{C}}[/латекс] перемещается с вашего пальца на металлическую дверную ручку в [латексе]\ жирныйсимвол{1. 00 \;\mu \textbf{s}}[/latex]?

4: Найдите силу тока, когда 2,00 нКл прыгает между расческой и волосами за интервал времени 0,500 – [латекс]\мю\текстбф{с}[/латекс].

5: Большая молния имела силу тока 20 000 А и заряд 30,0 Кл. Какова была его продолжительность?

6: Ток 200 А через свечу зажигания перемещает заряд 0,300 мКл. Как долго держится искра?

7: (a) Дефибриллятор посылает ток силой 6,00 А через грудную клетку пациента, применяя потенциал 10 000 В, как показано на рисунке ниже. Чему равно сопротивление пути? (b) Лопасти дефибриллятора соприкасаются с пациентом через проводящий гель, который значительно снижает сопротивление пути. Обсудите трудности, которые возникли бы, если бы большее напряжение использовалось для получения того же тока через пациента, но с сопротивлением пути, возможно, в 50 раз превышающим сопротивление. (Подсказка: ток должен быть примерно таким же, поэтому более высокое напряжение будет означать большую мощность.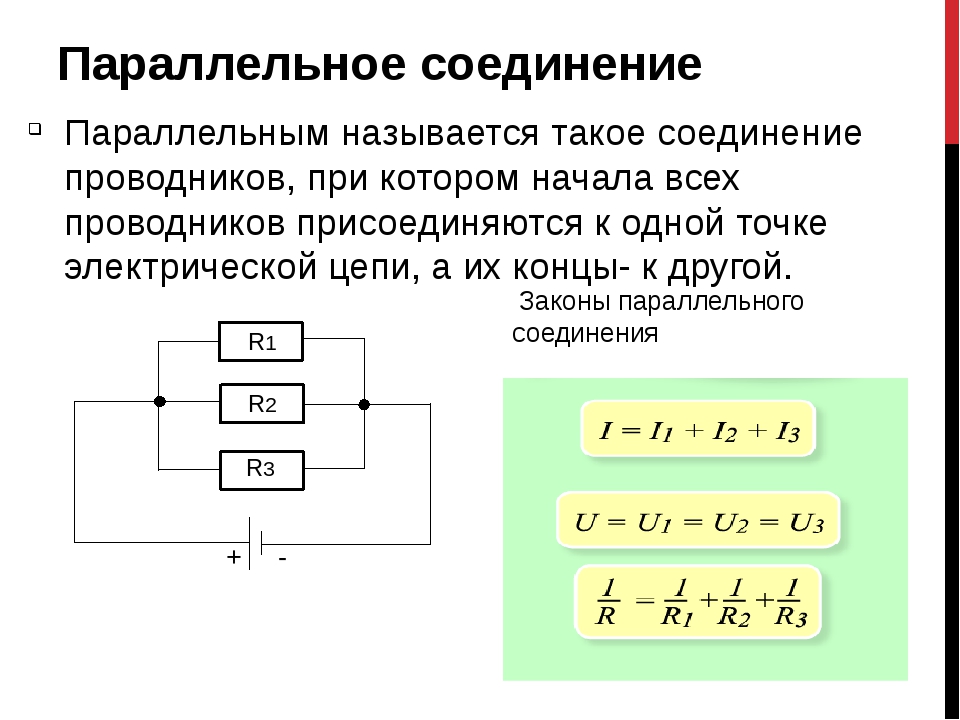 2 R}[/латекс].)

Рисунок 7. Конденсатор в дефибрилляторе пропускает ток через сердце пациента

8: Во время операции на открытом сердце дефибриллятор может быть использован для выведения пациента из состояния остановки сердца. Сопротивление пути составляет [латекс]\boldsymbol{500 \;\Omega }[/латекс], и необходим ток 10,0 мА. Какое напряжение должно быть подано?

9: (а) Дефибриллятор пропускает ток силой 12,0 А через туловище человека за 0,0100 с. Сколько заряда перемещается? б) Сколько электронов проходит по проводам, подсоединенным к пациенту? (См. рисунок две проблемы выше.) 9{++}}[/latex] ядра поражают цель?

14: Повторить приведенный выше пример на Примере 3, но для проволоки из серебра и дан один свободный электрон на атом серебра.

15: Используя результаты приведенного выше примера на Примере 3, найти скорость дрейфа в медной проволоке двойного диаметра и несущей ток 20,0 А.