Содержание
Длина волны — формулы, измерение, определение
Покажем, как применять знание физики в жизни
Начать учиться
Морские волны — далеко не все примеры волн. И длина волны — это не серферская характеристика, а вполне себе физическая величина. Сегодня разберемся, что такое волна и как ее охарактеризовать.
Волна: продольная и поперечная
Начнем с того, что волна — это распространение колебания в пространстве.
Волны бывают механическими и электромагнитными.
Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.
- Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.
Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.
Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.
Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.
Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.
Электромагнитные волны — это те волны, которые мы потрогать не можем.
- Например, радиоволны, Wi-Fi и свет.
Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 108 м/с.
Волны также принято делить на продольные и поперечные:
Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.
- Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.
Поперечные — волны, у которых колебание происходит поперек направления распространения волны.
- Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
- Видимый свет и дрожание гитарной струны — тоже поперечные волны.
Морская волна — продольная или поперечная?
На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Длина волны: определение и расчет
Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.
- λ — длина волны [м]
Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».
Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.
Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.
|
Формула периода колебания волны T = t/N T — период [с] t — время [с] N — количество колебаний [—] |
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
|
Формула скорости 𝑣 = S/t 𝑣 — скорость [м/с] S — путь [м] t — время [с] |
Переходя к волнам, можно провести следующие аналогии:
- путь — длина волны
- время — период
А для скорости даже аналогия не нужна — скорость и в Африке скорость.
|
Формула скорости волны 𝑣 = λ/T 𝑣 — скорость [м/с] λ — длина волны [м] T — период [с] |
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
- Возьмем формулу скорости:
- Нам известна длина волны, но не дан период.
Период вычисляется по формуле:
- Теперь подставляем величины в формулу
𝑣 = λ/T
T = t/N
T = 40/10 = 4 с
𝑣 = λ/T
𝑣 = ¼ = 0,25 м/с
Ответ: 𝑣 = 0,25 м/с
Резонанс
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.
На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.
Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.
|
Формула частоты ν = N/t ν — частота [Гц] t — время [с] N — количество колебаний [—] |
В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились.
Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.
В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.
Карина Хачатурян
К предыдущей статье
Сила тяжести
К следующей статье
Плотность вещества
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
-
Выявим пробелы в знаниях и дадим советы по обучению
-
Расскажем, как проходят занятия
-
Подберём курс
Перевод длины волны в частоту для всего диапазона электромагнитных колебаний
Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение,
видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.
Электромагнитные колебания — это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении
напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны
(Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое
излучение, рентгеновские либо гамма-лучи.
Рис.1
Длина волны, обозначаемая буквой λ и измеряемая в метрах —
это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.
Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс
повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.
Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).
Скорость распространения электромагнитных волн в вакууме (v) равна скорости
света и составляет величину:
v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где
n > 1 — это показатель преломления среды.
Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому
с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве.
Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).
И окончательно для воздушной среды:
λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).
Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн,
которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.
| Диапазон | Полоса частот | Длина волны |
| Сверхдлинные радиоволны | 3…30 кГц | 100000…10000 м |
| Длинные радиоволны | 30…300 кГц | 10000…1000 м |
| Средние радиоволны | 300…3000 кГц | 1000…100 м |
| Короткие радиоволны | 3…30 МГц | 100. ..10 м ..10 м |
| Метровый радиодиапазон | 30…300 МГц | 10…1 м |
| Дециметровый радиодиапазон | 300…3000 МГц | 1…0,1 м |
| Сантиметровый СВЧ диапазон | 3…30 ГГц | 10…1 см |
| Микроволновый СВЧ диапазон | 30…300 ГГц | 1…0,1 см |
| Инфракрасное излучение | 0,3…405 ТГц | 1000…0,74 мкм |
| Красный цвет | 405. ..480 ТГц ..480 ТГц |
740…625 нм |
| Оранжевый цвет | 480…510 ТГц | 625…590 нм |
| Жёлтый цвет | 510…530 ТГц | 590…565 нм |
| Зелёный цвет | 530…600 ТГц | 565…500 нм |
| Голубой цвет | 600…620 ТГц | 500…485 нм |
| Синий цвет | 620…680 ТГц | 485…440 нм |
| Фиолетовый цвет | 680. ..790 ТГц ..790 ТГц |
440…380 нм |
| Ультрафиолетовое излучение | 480…30000 ТГц | 400…10 нм |
| Рентгеновское излучение | 30000…3000000 ТГц | 10…0,1 нм |
| Гамма излучение | 3000000…30000000 ТГц | 0,1…0,01 нм |
А теперь можно переходить к калькуляторам.
КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ
|
Частота электромагнитных колебаний f |
|
кГц (10³ Гц)МГц (10⁶ Гц) ГГц (10⁹ Гц)ТГц (10¹² Гц) |
|
Показатель преломления среды (по умолч.  1) 1) |
|
|
|
|
||
|
Длина волны |
|
КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ
В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь
существует некоторая путаница. Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме,
т. е. численно равной Kp = 1/n, где n — это, как мы помним, показатель преломления среды.
Другие, наоборот — как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду — если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а
если Kp
13.

Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Определять амплитуду, частоту, период, длину волны и скорость волны
- Связь частоты волны, периода, длины волны и скорости
- Решение задач, связанных со свойствами волн
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (7) Научные понятия. Учащийся знает характеристики и поведение волн. Ожидается, что студент:
-
(Б)
исследовать и анализировать характеристики волн, включая скорость, частоту, амплитуду и длину волны, и рассчитывать, используя взаимосвязь между скоростью волны, частотой и длиной волны; -
(Д)
исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.
-
(Б)
Основные термины раздела
| длина волны | скорость волны |
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Проверьте амплитуду, период и частоту для простого гармонического движения.
Волновые переменные
В главе о движении в двух измерениях мы определили следующие переменные для описания гармонического движения:
- Амплитуда — максимальное смещение от положения равновесия объекта, колеблющегося вокруг такого положения равновесия
- Частота — количество событий в единицу времени
- Период — время, необходимое для совершения одного колебания
Для волн эти переменные имеют одинаковое основное значение. Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
- Амплитуда — расстояние между положением покоя и максимальным смещением волны
- Частота — количество волн, проходящих через определенную точку в секунду
- Период — время, необходимое для завершения одного цикла волны
Волны характеризуют не только амплитуда, частота и период, но и их длина волны и скорость волны.
Советы для успеха
Скорость волны иногда также называют скоростью распространения или скоростью распространения , поскольку возмущение распространяется из одного места в другое.
Рассмотрим периодическую волну воды на рис. 13.7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины. Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны Т . На рисунке сама волна движется вправо со скоростью волны v w . Его амплитуда X — это расстояние между положением покоя и максимальным смещением — либо гребнем, либо впадиной — волны.
Рисунок
13,7
Волна имеет длину волны λ , что является расстоянием между соседними одинаковыми частями волны. Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v w .
Смотреть физику
Амплитуда, период, частота и длина волны периодических волн
Данное видео является продолжением видео «Введение в волны» из раздела «Виды волн». В нем обсуждаются свойства периодической волны: амплитуда, период, частота, длина волны и скорость волны.
Советы для успеха
Гребень волны иногда также называют пиком .
Смотреть Физика: амплитуда, период, частота и длина волны периодических волн.
В этом видео представлены несколько концепций звука; амплитуда, период, частота и длина волны периодических волн.
Нажмите, чтобы просмотреть содержимое
Если вы находитесь на лодке в ложбине волны в океане, и амплитуда волны составляет 1\,\text{м}, какова высота волны с вашего местоположения?
-
1\,\текст{м}
-
2\,\текст{м}
-
4\,\текст{м}
-
8\,\текст{м}
Взаимосвязь между частотой волны, периодом, длиной волны и скоростью
Поскольку частота волны — это количество волн в секунду, а период — это, по сути, количество секунд на волну, соотношение между частотой и периодом составляет
f=1Tf=1T
13,1
или
T=1f,T=1f,
13,2
так же, как и в случае гармонического движения объекта.
Скорость распространения v w — это расстояние, которое волна проходит за заданное время, которое составляет одну длину волны за время одного периода. В форме уравнения это записывается как
vw=λTvw=λT
13,3
или
vw=fλ.vw=fλ.
13,4
Из этого соотношения мы видим, что в среде, где v w постоянно, чем выше частота, тем меньше длина волны. См. рисунок 13.8.
Рисунок
13,8
Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.
Поддержка учителей
Поддержка учителей
[BL] Для звука более высокая частота соответствует более высокому тону, а более низкая частота соответствует более низкому тону. Амплитуда соответствует громкости звука.
[BL][OL] Поскольку звук на всех частотах имеет одинаковую скорость в воздухе, изменение частоты означает изменение длины волны.
[Поддержка рисунка] Один и тот же динамик способен воспроизводить как высокочастотные, так и низкочастотные звуки. Однако высокие частоты имеют более короткую длину волны и, следовательно, лучше всего воспроизводятся динамиком с маленьким, твердым и плотным диффузором (твитер), тогда как более низкие частоты лучше всего воспроизводятся с большим и мягким диффузором (вуфер).
Эти фундаментальные соотношения справедливы для всех типов волн. Например, для волн на воде v w — это скорость поверхностной волны; для звука v w — скорость звука; а для видимого света v w — это скорость света.
Снап Лаборатория
Волны в миске
В этой лаборатории вы проведете измерения, чтобы определить, как на амплитуду и период волн влияет передача энергии от пробки, брошенной в воду. Пробка изначально обладает некоторой потенциальной энергией, когда ее держат над водой — чем больше высота, тем выше потенциальная энергия. Когда пробка падает, такая потенциальная энергия преобразуется в кинетическую энергию, когда пробка падает. Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
- Большая миска или таз
- Вода
- Пробка (или мячик для пинг-понга)
- Секундомер
- Рулетка
Инструкции
Процедура
- Наполните большую миску или таз водой и подождите, пока вода не осядет, чтобы не было ряби.
- Аккуратно бросьте пробку в середину чаши.
- Оцените длину волны и период колебаний водной волны, распространяющейся от пробки. Вы можете оценить период, подсчитав количество ряби от центра к краю чаши, пока ваш партнер измеряет это время. Эта информация в сочетании с измерением чаши даст вам длину волны при использовании правильной формулы.
- Выньте пробку из миски и подождите, пока вода снова не осядет.
- Аккуратно бросьте пробку с высоты, отличной от высоты первого падения.
- Повторите шаги с 3 по 5, чтобы собрать второй и третий наборы данных, сбрасывая пробку с разной высоты и записывая полученные длины волн и периоды.
- Интерпретируйте свои результаты.
Пробка падает в бассейн с водой, создавая волны. Зависит ли длина волны от высоты над водой, с которой брошена пробка?
-
Нет, влияет только на амплитуду.
-
Да, длина волны затронута.
Поддержка учителей
Поддержка учителей
Учащиеся могут заранее измерить чашу, чтобы лучше оценить длину волны.
Виртуальная физика
Волна на струне
В этой анимации посмотрите, как струна вибрирует в замедленном темпе, выбрав параметр «Замедленное движение». Выберите параметры «Без конца» и «Вручную» и покачивайте конец струны, чтобы создавать волны самостоятельно. Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.
Проверка захвата
Какая из настроек — амплитуда, частота, затухание или натяжение — изменяет амплитуду волны при ее распространении? Что он делает с амплитудой?
- Частота; он уменьшает амплитуду волны по мере ее распространения.
- Частота; он увеличивает амплитуду волны по мере ее распространения.
- Демпфирование; он уменьшает амплитуду волны по мере ее распространения.
- Демпфирование; он увеличивает амплитуду волны по мере ее распространения.
Решение волновых задач
Рабочий пример
Рассчитайте скорость распространения волн: Чайка в океане
Рассчитайте скорость морской волны на предыдущем рисунке, если расстояние между гребнями волн равно 10,0 м, а время, за которое чайка качается вверх и вниз, составляет 5,00 с.
Стратегия
Заданы значения длины волны (λ=10,0 м)(λ=10,0 м) и периода (T=5,00 с)(T=5,00 с), и нас просят найти vwvw Следовательно, мы можем использовать vw= λTvw=λT, чтобы найти скорость волны.
Решение
Введите известные значения в vw=λTvw=λT
vw=10,0 м5,00 с=2,00 м/с.vw=10,0 м5,00 с=2,00 м/с.
13.
Обсуждение
Такая низкая скорость кажется приемлемой для океанской волны. Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Рабочий пример
Вычислите период и скорость волны игрушечной пружины.
Женщина на рис. 13.3 создает две волны каждую секунду, встряхивая игрушечную пружину вверх и вниз. а) Каков период каждой волны? (b) Если каждая волна проходит 0,9 метра после одного полного волнового цикла, какова скорость распространения волны?
Стратегия ЗА (А)
Чтобы найти период, мы решаем T=1fT=1f, учитывая значение частоты (f=2s−1).(f=2s−1).
Решение для (a)
Введите известное значение в T=1fT=1f
T=12 с-1=0,5 с. T=12 с-1=0,5 с.
13,6
Стратегия ЗА (Б)
Поскольку одним из определений длины волны является расстояние, пройденное волной за один полный цикл или один период, приводятся значения длины волны (λ=0,9 м)(λ=0,9 м), а также частоты.
Решение для (b)
Введите известные значения в vw=fλvw=fλ
vw=fλ=(2 с-1)(0,9 м) = 1,8 м/с. vw=fλ=(2 с-1)(0,9 м) = 1,8 м/с.
Обсуждение
Мы могли бы также использовать уравнение vw=λTvw=λT для определения скорости волны, поскольку мы уже знаем значение периода (T=0,5 с)(T=0,5 с) из нашего расчета в части ( а), и мы бы пришли к тому же ответу.
Практические задачи
7.
Частота волны 10 Гц. Каков его период?
- Период волны 100 с.
- Период волны 10 с.
- Период волны 0,01 с.
- Период волны 0,1 с.
8.
Какова скорость волны с длиной волны 2 м и частотой 5 Гц?
- 20 м/с
- 2,5 м/с
- 0,4 м/с
- 10 м/с
Проверьте свое понимание
Поддержка учителей
Поддержка учителей
Используйте эти вопросы, чтобы оценить достижения учащихся в соответствии с целями обучения данного раздела.
9.
Какова амплитуда волны?
- Четверть общей высоты волны
- Половина общей высоты волны
- Удвоенная общая высота волны
- Четырехкратная общая высота волны
10.
Что понимают под длиной волны?
-
Длина волны — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения.
-
Длина волны — это расстояние между соседними одинаковыми частями волны, перпендикулярное направлению распространения.
-
Длина волны — это расстояние между гребнем и прилегающей впадиной волны, параллельное направлению распространения.
- 92
12.
Когда длина волны прямо пропорциональна периоду волны?
- Когда скорость волны уменьшается вдвое
- Когда скорость волны постоянна
- Когда скорость волны удваивается
- Когда скорость волны утроится
Учебник по физике: волновое уравнение
Как обсуждалось в Уроке 1, волна возникает, когда вибрирующий источник периодически возмущает первую частицу среды. Это создает волновую картину, которая начинает перемещаться по среде от частицы к частице. Частота, с которой вибрирует каждая отдельная частица, равна частоте, с которой вибрирует источник. Точно так же период колебаний каждой отдельной частицы в среде равен периоду колебаний источника. За один период источник может сместить первую частицу из состояния покоя вверх, обратно в состояние покоя, вниз из состояния покоя и, наконец, обратно в состояние покоя.
Диаграммы справа показывают несколько «моментальных снимков» образования волны внутри веревки. Изображено движение возмущения по среде через каждую четвертую периода. Обратите внимание, что за время, которое проходит от первого до последнего снимка, рука сделала одно полное движение вперед-назад. Прошел период. Обратите внимание, что за это же время передний фронт возмущения переместился на расстояние, равное одной полной длине волны. Таким образом, за время одного периода волна прошла расстояние в одну длину волны. Объединив эту информацию с уравнением скорости (скорость = расстояние/время), можно сказать, что скорость волны также является длиной волны/периодом.
Поскольку период обратно пропорционален частоте, выражение 1/f можно подставить в приведенное выше уравнение для периода. Преобразование уравнения дает новое уравнение вида:
Приведенное выше уравнение известно как волновое уравнение.
В качестве проверки вашего понимания волнового уравнения и его математического использования при анализе волнового движения рассмотрите следующие три: часть вопроса:
Стэн и Анна проводят хитрый эксперимент. Они изучают возможное влияние нескольких переменных на скорость волны в слинки. Их таблица данных показана ниже. Заполните пропуски в таблице, проанализируйте данные и ответьте на следующие вопросы.
|
|
|
|
|
|
1 дюйм. |
|
|
|
|
1 дюйм. диам. катушки |
|
|
|
|
1-дюйм. диам. катушки |
|
|
|
|
1 дюйм. диам. катушки |
|
|
|
|
3 дюйма диам. катушки |
|
|
|
|
3 дюйма диам. |
|
|
|
1. При увеличении длины волны в однородной среде ее скорость будет _____.
|
а. уменьшить |
б. увеличить |
в. остаются прежними |
2. При увеличении длины волны в однородной среде ее частота будет _____.
|
а. уменьшить |
б. увеличить |
в. остаются прежними |
3. Скорость волны зависит (т. е. причинно зависит от) …
а. свойства среды, через которую распространяется волна
б. длина волны.
в. частота волны.
д.
как длина волны, так и частота волны.
В приведенном выше примере показано, как использовать волновое уравнение для решения математических задач. Это также иллюстрирует принцип, согласно которому скорость волны зависит от свойств среды и не зависит от свойств волны. Хотя скорость волны рассчитывается путем умножения длины волны на частоту, изменение длины волны не влияет на скорость волны. Скорее, изменение длины волны влияет на частоту обратным образом. Удвоение длины волны приводит к уменьшению вдвое частоты; но скорость волны не изменилась.
1. Две волны на одинаковых струнах имеют частоты в отношении 2 к 1. Если скорости их волн одинаковы, то как длины волн сравнить?
а. 2:1
б.
1:2
в. 4:1
д. 1:4
2. Мак и Тош стоят на расстоянии 8 метров друг от друга и демонстрируют движение поперечной волны на змейке. Волну e можно описать как имеющую расстояние по вертикали от ложбины до гребня 32 см, частоту 2,4 Гц и расстояние по горизонтали 48 см от гребня до ближайшей ложбины. Определите амплитуду, период, длину волны и скорость такой волны.
3. Дон и Арам натянули между собой облегающий костюм и начали экспериментировать с волнами. Поскольку частота волн удваивается,
а. длина волны уменьшается вдвое, а скорость остается постоянной
б. длина волны остается постоянной, а скорость удваивается
в. и длина волны, и скорость уменьшаются вдвое.
д. и длина волны, и скорость остаются постоянными.
4.
 Период вычисляется по формуле:
Период вычисляется по формуле:



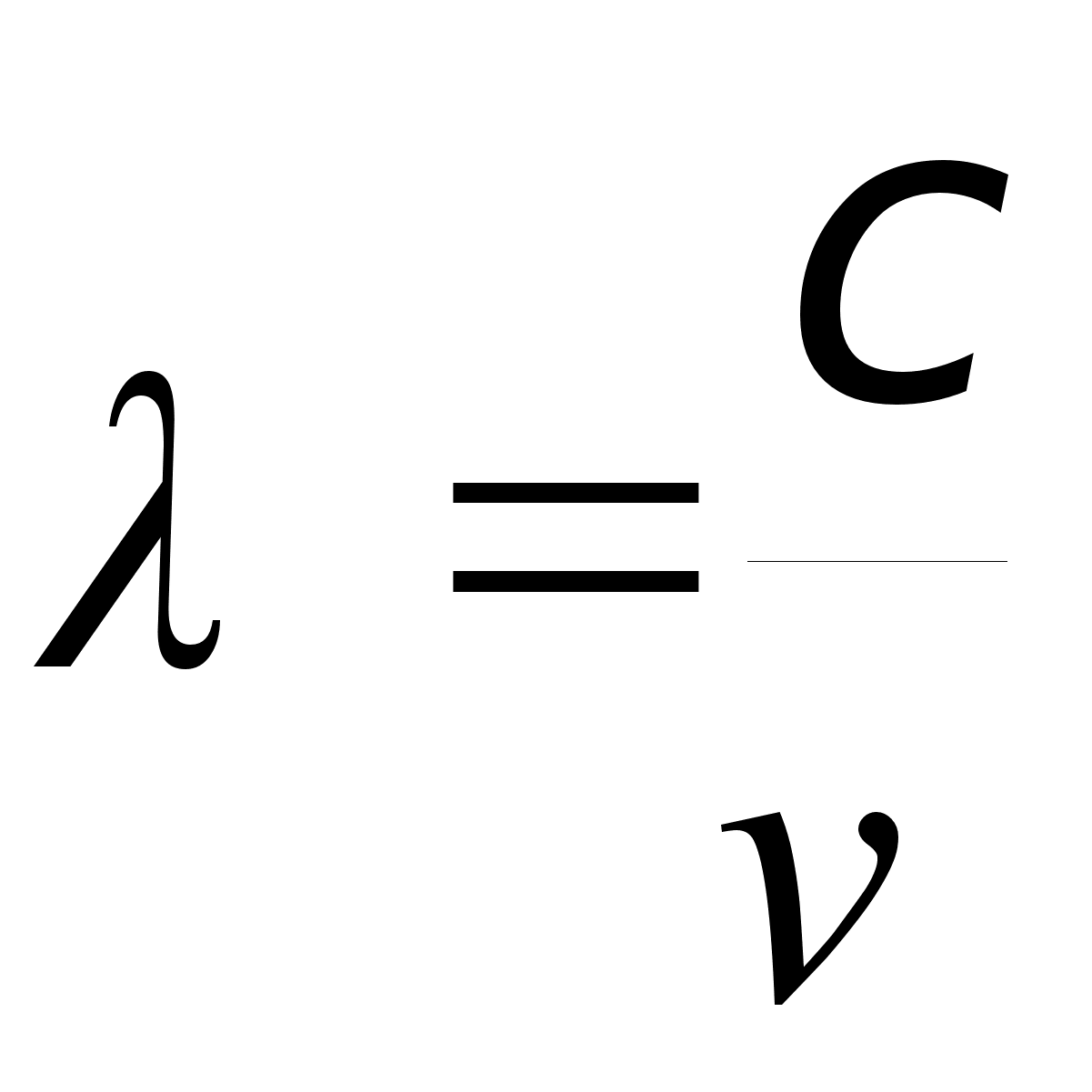
 диам. катушки
диам. катушки  катушки
катушки  как длина волны, так и частота волны.
как длина волны, так и частота волны.  1:2
1:2 
Добавить комментарий