Содержание
Законы Кирхгофа для расчёта электрических цепей
При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.
Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.
Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза [1].
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:
$$ \sum{i} = 0, $$
или в комплексной форме
$$ \sum{\underline{I}} = 0. $$
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:
$$ \sum{\underline{Z} \cdot \underline{I}} = \sum{\underline{E}}. $$
Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно $ N_\textrm{у}-1 $, где $ N_\textrm{у} $ – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно $ N_\textrm{в}-N_\textrm{у}+1 $, где $ N_\textrm{в} $ – число ветвей.
Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.
Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.
Рис. 1. Рассматриваемая электрическая цепь
Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).
Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи
Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока $ \underline{J}_{1} $, не рассматривается.
Составим уравнения по первому закону Кирхгофа.
Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:
$$ \underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3} = 0; $$
для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:
$$ -\underline{I}_{1}- \underline{I}_{4} + \underline{I}_{6} = 0; $$
для узла «3 у.»:
$$ \underline{I}_{2}+ \underline{I}_{4} + \underline{I}_{5}- \underline{I}_{7} = 0; $$
для узла «4 у.»:
$$ \underline{I}_{3}- \underline{I}_{5}- \underline{J}_{1} = 0. $$
Уравнение для узла «5 у.» можно не составлять.
Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:
$$ \underline{Z}_{C1} \cdot \underline{I}_{1} + R_{2} \cdot \underline{I}_{2}- \underline{Z}_{L1} \cdot \underline{I}_{4} = \underline{E}_{1}; $$
для контура «2 к.
» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:
$$ -R_{2} \cdot \underline{I}_{2} + R_{4} \cdot \underline{I}_{3} + \underline{Z}_{C2} \cdot \underline{I}_{5} = \underline{E}_{2}; $$
для контура «3 к.»:
$$ \underline{Z}_{L1} \cdot \underline{I}_{4} + (\underline{Z}_{L2} + R_{1}) \cdot \underline{I}_{6} + R_{3} \cdot \underline{I}_{7} = \underline{E}_{3}; $$
где $ \underline{Z}_{C} = -\frac{1}{\omega C} $, $ \underline{Z}_{L} = \omega L $.
Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:
$$ \begin{cases} \underline{I}_{1}- \underline{I}_{2}- \underline{I}_{3} = 0 \\ -\underline{I}_{1}- \underline{I}_{4} + \underline{I}_{6} = 0 \\ \underline{I}_{2}+ \underline{I}_{4} + \underline{I}_{5}- \underline{I}_{7} = 0 \\ \underline{I}_{3}- \underline{I}_{5}- \underline{J}_{1} = 0 \\ \underline{Z}_{C1} \cdot \underline{I}_{1} + R_{2} \cdot \underline{I}_{2}- \underline{Z}_{L1} \cdot \underline{I}_{4} = \underline{E}_{1} \\ -R_{2} \cdot \underline{I}_{2} + R_{4} \cdot \underline{I}_{3} + \underline{Z}_{C2} \cdot \underline{I}_{5} = \underline{E}_{2} \\ \underline{Z}_{L1} \cdot \underline{I}_{4} + (\underline{Z}_{L2} + R_{1}) \cdot \underline{I}_{6} + R_{3} \cdot \underline{I}_{7} = \underline{E}_{3} \end{cases} $$
В данном случае это система из 7 уравнений с 7 неизвестными.
Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:
$$ \begin{bmatrix} 1 & -1 & -1 & 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & -1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 1 & 0 & -1 & 0 & 0 \\ \underline{Z}_{C1} & R_{2} & 0 & -\underline{Z}_{L1} & 0 & 0 & 0 \\ 0 & -R_{2} & R_{4} & 0 & \underline{Z}_{C2} & 0 & 0 \\ 0 & 0 & 0 & \underline{Z}_{L1} & 0 & R_{1}+\underline{Z}_{L2} & R_{3} \\ \end{bmatrix} \cdot \begin{bmatrix} \underline{I}_{1} \\ \underline{I}_{2} \\ \underline{I}_{3} \\ \underline{I}_{4} \\ \underline{I}_{5} \\ \underline{I}_{6} \\ \underline{I}_{7} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \underline{J}_{1} \\ \underline{E}_{1} \\ \underline{E}_{2} \\ \underline{E}_{3} \\ \end{bmatrix} $$
Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:
>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3;
>> A = [1 -1 -1 0 0 0 0;
-1 0 0 -1 0 1 0;
0 1 0 1 1 0 -1;
0 0 1 0 -1 0 0;
Zc1 R2 0 -Zl1 0 0 0;
0 -R2 R4 0 Zc2 0 0;
0 0 0 Zl1 0 (R1+Zl2) R3];
>> b = [0;
0;
0;
J1;
E1;
E2;
E3];
>> I = A\b
В результате получим вектор-столбец $ \underline{\bold{I}} $ токов из семи элементов, состоящий из искомых токов, записанный в общем виде.
Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
1) Составить уравнения по законам Кирхгофа.
Некоммерческое
акционерное общество
«АЛМАТИНСКИЙ
УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра
теоретических основ электротехники
РАСЧЕТНО-ГРАФИЧЕСКАЯ
РАБОТА №1
По
дисциплине «Основы теории цепей»
На
тему «Расчет линейных электрических
цепей постоянного тока с зависимыми
источниками»
Специальность
«Информационные системы»
Выполнил
Ануарбеков Шыңғыс
Группа ИС-16-2
Принял
доцент каф. ТОЭ Айтжанов Н.М.
_________
«____»____________2017г.
Алматы
2017
Содержание
Введение……………………………………………………………………………………………………3
Задание………………………………………………………………………………………………………4
Расчетная
часть………………………………………………………………………………………….6
Уравнения
по законам
Кирхгофа………………………………………………………..6
Метод
контурных
токов……………………………………………………………………..7
Метод
узловых
потенциалов………………………………………………………………9
Сравнение
результатов МКТ и
МУП…………………………………………………10
Метод
эквивалентного
генератора.
…………………………………………………….11
Напряжение
на зажимах источника
тока……………………………………………13
Баланс
мощностей…………………………………………………………………………….13
Заключение………………………………………………………………………………………………14
Список
литературы…………………………………………………………………………………..15
Введение
Цель работы: умение составлять систему уравнений по законам
Кир-хгофа; применение закона Ома;
получение навыков расчётов электрических
цепей постоянного тока
с
зависимыми источниками методами
контурных токов, методом узловых
потенциалов, эквивалентного генератора.
В
цепи действуют независимые источники
напряжения с ЭДС Е1,
Е2,
Е3,
источник тока J
и зависимый источник напряжения
Еи
,
управляемый током.
Номер схемы определяется
по таблице 1.1, числовые значения параметров
цепи приведены в таблицах 1.2 и 1.3.
Таблица
1.1
|
Год |
Первая |
|||||||||
|
Четный |
А |
ГЭЕ |
ЖЗЩ |
КЛ |
МН |
ОПР |
СТУ |
ФЧЦ |
ХШИ |
ДЮВ |
|
№ схемы |
1. |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
1.9 |
1.10 |
|
МЭГ |
I1 |
I3 |
I4 |
I2 |
I1 |
I4 |
I3 |
I3 |
I1 |
I2 |
1Таблица
1.
2
|
Год |
Последняя |
|||||||||
|
Четный |
0 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
E1, |
25 |
20 |
30 |
40 |
20 |
25 |
15 |
35 |
40 |
15 |
|
E2, |
10 |
15 |
25 |
20 |
30 |
20 |
15 |
10 |
20 |
25 |
|
E3, |
25 |
30 |
35 |
20 |
30 |
20 |
25 |
15 |
30 |
10 |
|
J, |
3 |
5 |
2 |
6 |
4 |
10 |
8 |
5 |
3 |
5 |
|
r, |
10 |
20 |
15 |
16 |
25 |
30 |
35 |
40 |
15 |
20 |
Таблица
1.
3
|
Год |
Предпоследняя |
|||||||||
|
Четный |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
R1, |
25 |
20 |
15 |
20 |
10 |
30 |
20 |
10 |
30 |
15 |
|
R2, |
15 |
30 |
20 |
12 |
20 |
10 |
20 |
25 |
40 |
20 |
|
R3, |
20 |
16 |
25 |
35 |
30 |
20 |
30 |
16 |
10 |
30 |
|
R4, |
30 |
20 |
30 |
40 |
15 |
40 |
15 |
25 |
20 |
30 |
|
R, |
6 |
10 |
8 |
10 |
10 |
15 |
20 |
15 |
5 |
8 |
Рисунок 1.
1
Задание:
1)
Составить
уравнения по законам Кирхгофа.
2)
Рассчитать
токи во всех ветвях методом контурных
токов.
3) Рассчитать
токи во всех ветвях методом узловых
потенциалов. 4) Сравнить
результаты, полученные в пунктах 2, 3 и
свести их в
одну
таблицу.
5)
Рассчитать
ток в одной ветви методом эквивалентного
генератора (см. таблицу 1.1).
6)
Определить напряжение на зажимах
источника тока.
7)
Проверить выполнение баланса мощности.
Расчетная
часть
Первый
закон Кирхгофа: алгебраическая сумма
токов в узле электрической цепи равна
нулю:
.
Со знаком «+» записываются токи,
направленные к узлу, со знаком «-»
записываются токи, направленные от узла
(или наоборот). Число уравнений,
составляемых по первому закону Кирхгофа,
равно
,
где
—
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений по I
закону Кирхгофа).
Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3.
Второй
закон Кирхгофа: в любом замкнутом контуре
электрической цепи алгебраическая
сумма напряжений на сопротивлениях,
входящих в этот контур равна алгебраической
сумме ЭДС:
.
Напряжения
записываются со знаком «+», если
положительное направление тока
совпадает с направлением обхода контура,
со знаком «-», если направление тока
противоположно
направлению обхода контура; ЭДС
,
направления, которых совпадают с
направлением обхода контура, записываются
со знаком «+», а ЭДС
,
направленные против обхода контура –
со знаком «-». Число уравнений, составляемых
по второму закону Кирхгофа, равно:
,
где
— число ветвей,
— число источников тока. Исходя из этого,
в цепи (рис 1.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 1.
1). И для
каждого контура (внешний контур и контур
1241) запишем уравнение по II
закону Кирхгофа:
Общая
система уравнений по законам Кирхгофа
будет выглядеть следующим образом
Составим
систему уравнений по методу контурных
токов для цепи постоянного тока (рис
1.2):
Рисунок
1.2.
,
где
=
(
Решение:
=
=
=
=
=
=
=
=
,
тогда
=7,73
– 7,53 = 0,2А
=
7,53А
=
7,73А
=
10 – 7,53 = 2,47А
=
010– 7,73 = 2,27А
3) Рассчитать
токи во всех ветвях методом узловых
потенциалов.
Метод
узловых потенциалов позволяет уменьшить
число уравнений системы до числа
.
Суть
метода
узловых потенциалов заключается в
определении потенциалов узлов
электрической цепи, токи рассчитываются
по закону Ома. При составлении уравнений
по методу узловых потенциалов, потенциал
одного из узлов принимают равным нулю,
для определения потенциалов оставшихся
узлов составляются уравнения.
Возьмем
узел 3 за базовый и будем считать, что
он равен нулю. Автоматически значение
потенциала в узле 4 становится равным
.
().
Составим
систему уравнений по методу узловых
потенциалов для цепи постоянного тока
(рис 1.3), так как значения потенциалов в
узлах 3 и 4 известны, то нам необходимо
составить систему из 2 уравнений для
узлов 1 и 2:
Рисунок
1.3
найдем,
применив I
закон Кирхгофа
Решение:
,
тогда
=0,99*68,2694
= 67,586706В
=
0,115 А
=
7,47А
=
2,46А
=
2,25А
7,35А
правил Кирхгофа | Физика
Цели обучения
К концу этого раздела вы сможете:
- Анализировать сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных членов.
Многие сложные схемы, такие как схема на рис. 1, не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в разделе Резисторы в последовательном и параллельном соединении и Электродвижущая сила: напряжение на клеммах. Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).
Рис. 1. Эту схему нельзя свести к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание: буква E на рисунке обозначает электродвижущую силу, эдс.)
Правила Кирхгофа
- Первое правило Кирхгофа — правило пересечения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
- Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.
Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения ) является применением закона сохранения заряда к соединению; это показано на рис. 2. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы I 1 = I 2 + I 3 (см. рисунок). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.
Установление соединений: законы сохранения
Правила Кирхгофа для анализа цепей представляют собой применение законов сохранения к цепям.
Первое правило — применение закона сохранения заряда, а второе правило — применение закона сохранения энергии. Законы сохранения, даже используемые в конкретных приложениях, таких как анализ цепей, настолько просты, что составляют основу этого приложения.
Рисунок 22. Правило соединения. На диаграмме показан пример первого правила Кирхгофа, в котором сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что I 1 = I 2 + I 3 . Здесь I 1 должно быть 11 А, так как I 2 равно 7 А, а I 3 равно 4 A.
Второе правило Кирхгофа
Второе правило Кирхгофа (правило цикла ) является применением закона сохранения энергии. Правило петли сформулировано с точки зрения потенциала, В , а не потенциальной энергии, но они связаны, поскольку PE elec = qV .
Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рисунке 3 показаны изменения потенциала в простой последовательной цепи. Второе правило Кирхгофа требует ЭДС − Ir − IR 1 − IR 2 = 0. Если переставить, это будет ЭДС = Ir + IR 9003 7 1 + IR 2 = 0, что означает ЭДС равно сумме IR (напряжения) падений в контуре.
Рис. 3. Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В.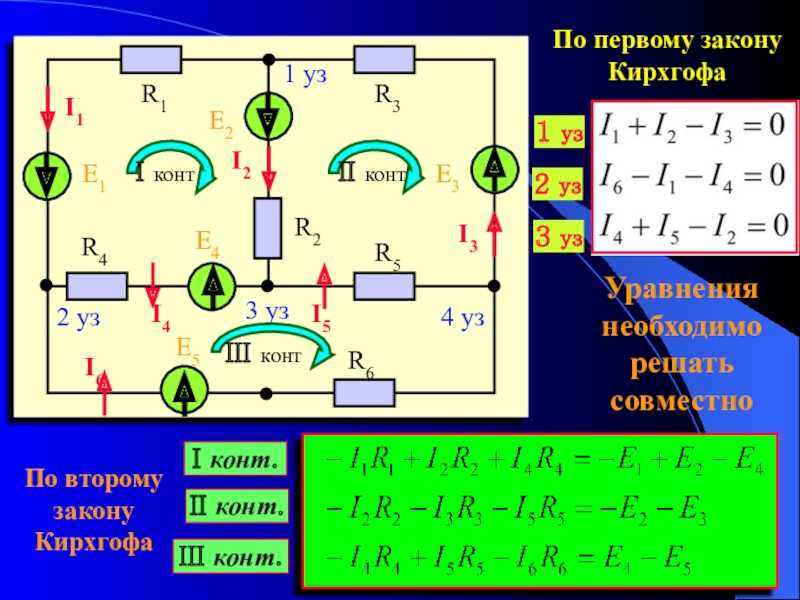
(b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС.)
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.
- Применяя первое правило Кирхгофа, правило соединения, вы должны пометить ток в каждой ветви и решить, в каком направлении он течет. Например, на рис. 1, рис. 2 и рис. 3 токи обозначены I 1 , I 2 , I 3 и I 9001. 2, а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
- Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рисунке 3 петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; Обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что похоже на умножение обеих частей уравнения на -1.
2, а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным. Рисунок 4 и следующие пункты помогут вам правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 4.)
Рисунок 4. Каждый из этих резисторов и источников напряжения проходит от a до b.
Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)
- Когда резистор перемещается в том же направлении, что и ток, изменение потенциала составляет −IR . (См. рис. 4.)
- Когда резистор перемещается в направлении, противоположном току, изменение потенциала составляет + IR . (См. рис. 4.)
- Когда ЭДС перемещается от – к + (в том же направлении, что и положительный заряд), изменение потенциала составляет +ЭДС. (См. рис. 4.)
- Когда ЭДС перемещается от + к — (противоположно направлению, в котором движется положительный заряд), изменение потенциала равно — ЭДС. (См. рис. 4.)
Пример 1. Расчет силы тока: использование правил Кирхгофа
Найдите токи, протекающие в цепи на рисунке 5.
Рисунок 5. Эта цепь аналогична схеме на рисунке 1, но сопротивления и ЭДС заданы. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях.
В этом примере для нахождения токов используются правила Кирхгофа.
Стратегия
Эта схема настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Токи были обозначены на рисунке I 1 , I 2 и I 3 , и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.
Решение
Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает
I 1 = I 2 + I 3 ,
начиная с I 1 впадает в узел, а I 2 и I 3 слив. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается.
Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла. Теперь рассмотрим петлю abcdea. Переходя от a к b, мы проходим R 2 в том же (предполагаемом) направлении тока I 2 , поэтому изменение потенциала равно − I 2 R 2 . Затем, переходя от b к c, мы переходим от – к +, так что изменение потенциала равно +ЭДС 1 . Пересечение внутреннего сопротивления r 1 от c к d дает − I 2 r 1 . Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала на — I 1 R 1 . Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,
− I 2 R 2 + ЭДС 1 − I 2 900 11 r 1 − I 1 R 1 = − I 2 ( R 2 + r 1 ) + ЭДС 1 − I 1 R 1 = 0,
Подстановка значений сопротивлений и ЭДС из принципиальной схемы и отмена единиц ампер дает
−3 I 2 + 18 − 6 900 11 I 1 = 0.
Теперь, применяя правило цикла к aefgha (мы могли бы выбрать и abcdefgha), аналогичным образом получаем
+ I 1 R 1 + I 90 012 3 Р 3 + я 3 r 2 − ЭДС 2 = + I 1 R 1 900 38 + I 3 ( R 3 + r 2 ) − ЭДС 2 = 0.
Обратите внимание, что знаки меняются местами по сравнению с другим контуром, потому что элементы проходятся в противоположном направлении. С введенными значениями это становится
+6 I 1 + 2 I 3 – 45 = 0,
Этих трех уравнений достаточно, чтобы решить для трех неизвестных токов. Сначала решим второе уравнение для I 2 :
I 2 = 6 − 2 I 1 .
Теперь решите третье уравнение для I 3 :
I 3 = 22,5 − 3 I 1 9003 8 .
Подстановка этих двух новых уравнений в первое позволяет нам найти значение для I 1 :
I 1 = I 2 + I 3 = (6−2 I 1 ) + (22,5−3 I ) 1 ) = 28,5 − 5 I 1 .
Объединение членов дает
6 I 1 = 28,5 и
I 1 = 4,75 А.
Подстановка этого значения вместо I 1 обратно в четвертое уравнение дает
I 2 = 6 − 2 I 1 = 6 − 9,50
I 2 = − 3,50 А.
Знак минус означает, что I 2 течет в направлении, противоположном предполагаемому на рис. 5. Наконец, подстановка значения I 1 в пятое уравнение дает 038 = 22,5 — 14 . 25
I 3 = 8,25 А.
Обсуждение
Просто для проверки отметим, что действительно I 1 = I 900 37 2 + I 3 .
Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.
Стратегии решения задач по правилам Кирхгофа
- Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
- Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение избыточно.
- Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.9.0008
- Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.
- Проверить разумность и последовательность ответов. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.
Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.9.0008
Материал в этом разделе теоретически верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для проведения таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях.
Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.
Проверьте свое понимание
Можно ли применять правила Кирхгофа к простым последовательным и параллельным цепям, или они ограничены для использования в более сложных цепях, которые не являются комбинацией последовательной и параллельной?
Решение
Правила Кирхгофа можно применить к любой схеме, поскольку они являются приложениями к схемам двух законов сохранения. Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Резюме раздела
- Правила Кирхгофа можно использовать для анализа любой схемы, простой или сложной.
- Первое правило Кирхгофа — правило соединения: сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
- Второе правило Кирхгофа — правило петли: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
- Два правила основаны соответственно на законах сохранения заряда и энергии.
- При расчете потенциала и тока по правилам Кирхгофа необходимо соблюдать ряд правил для определения правильных знаков различных членов.
- Простые ряды и параллельные правила являются частными случаями правил Кирхгофа.
Концептуальные вопросы
1. Могут ли все токи, входящие в соединение на рисунке 6, быть положительными? Объяснять.
Рисунок 6.
2. Примените правило соединения к соединению b на рис.
7. Получена ли какая-либо новая информация при применении правила соединения в точке e? (На рисунке каждая ЭДС представлена буквой Е.)
Рисунок 7.
3. (a) Какова разность потенциалов при переходе из точки a в точку b на рис. 7? б) Чему равна разность потенциалов при переходе от c к b? в) От е до g? (г) От е до d?
4. Примените правило цикла к циклу afedcba на рисунке 7.
5. Примените правило цикла к циклам abgefa и cbgedc на рисунке 7.
Задачи и упражнения
1. Примените правило цикла к циклу abcdefgha на рисунке 5 (показанном ниже).
Рис. 5. Эта схема аналогична схеме на рис. 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.
2. Примените петлевое правило к петле aedcba на рисунке 5.
3. Проверьте второе уравнение в Пример 1 Расчет тока: с использованием правил Кирхгофа (в тексте выше), путем подстановки найденных значений токов I 1 и I 2 .
4. Проверьте третье уравнение в Пример 1 Расчет тока: с использованием правил Кирхгофа (в тексте выше), подставив найденные значения токов I 1 и I 3 .
5. Примените правило соединения в точке a на рисунке 8.
Рисунок 8.
6. Примените правило цикла к кольцу abcdefghija на рисунке 8.
7. Примените правило цикла к кольцу akledcba на рисунке 8.
8. Найдите токи, протекающие в цепи на рисунке 8. В явном виде покажите, как вы выполняете шаги, описанные в Стратегии решения проблем для последовательных и параллельных резисторов выше.
9. Решите Пример 1 Расчет тока: с использованием правил Кирхгофа (в тексте выше), но используйте цикл abcdefgha вместо цикла akledcba. Явно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для последовательных и параллельных резисторов .
10. Найдите токи, протекающие в цепи на рисунке 7 (показанном ниже).
Рисунок 7.
11. Необоснованные результаты Рассмотрим схему на рисунке 9 и предположим, что ЭДС неизвестны, а токи заданы равными I 1 = 5,00 А, I 2 = 3,0 А и I 3 = –2,00 А. а) Не могли бы вы найти ЭДС? б) Что неверно в предположениях?
Рисунок 9.
Глоссарий
- Правила Кирхгофа:
- набор из двух правил, основанных на сохранении заряда и энергии, управляющих током и изменениями потенциала в электрической цепи
- правило соединения:
- первое правило Кирхгофа, применяющее закон сохранения заряда к соединению; ток — это поток заряда; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу; правило может быть указано [latex]{I}_{1}={I}_{2}+{I}_{3}[/latex]
- правило цикла:
- Второе правило Кирхгофа, которое гласит, что в замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. Таким образом, ЭДС равна сумме падений [латекс]\текст{IR}[/латекс] (напряжения) в контуре и может быть сформулирована следующим образом: [латекс]\текст{ЭДС}=\текст{Ir}+{\ text{IR}}_{1}+{\text{IR}}_{2}\\[/латекс]
Таким образом, ЭДС равна сумме падений [латекс]\текст{IR}[/латекс] (напряжения) в контуре и может быть сформулирована следующим образом: [латекс]\текст{ЭДС}=\текст{Ir}+{\ text{IR}}_{1}+{\text{IR}}_{2}\\[/латекс] - законов сохранения:
- требуют сохранения энергии и заряда в системе
Избранные решения задач и упражнений
1. [латекс]-{I}_{2}{R}_{2}+{\text{emf}}_{1}-{\text{I}} _{2}{r}_{1}+{\text{I}}_{3}{R}_{3}+{\text{I}}_{3}{r}_{2}- {\text{emf}}_{2}=\text{0}\\[/latex]
5. I 3 = I 1 + I 2
7. [поздно х] {\ text {ЭДС}} _ {2} — {\ text {I}} _ {2} {r} _ {2} — {\ text {I}} _ {2} {R} _ {2} + {\ text {I}} _ {1} {R} _ {5} + {I} _ {1} {r} _ {1} — {\ text {ЭДС}} _ {1} + {\ text { I}}_{1}{R}_{1}=0\\[/латекс]
9.(a) I 1 = 4,75 A (b) I 2 = −3,5 A (c) I 3 = 8,25 А
11. (а) Нет, вы получите противоречивые уравнения для решения.
(б) I 1 ≠ I 2 + I 3 . Предполагаемые токи нарушают правило соединения.
6.3 Правила Кирхгофа. Введение в электричество, магнетизм и электрические цепи
ЦЕЛИ ОБУЧЕНИЯ
К концу раздела вы сможете:
- Государственное правило пересечения Кирхгофа
- Государственное правило петли Кирхгофа
- Анализ сложных цепей с использованием правил Кирхгофа
Мы только что видели, что некоторые схемы можно анализировать, сводя схему к одному источнику напряжения и эквивалентному сопротивлению. Многие сложные схемы невозможно проанализировать с помощью последовательно-параллельных методов, разработанных в предыдущих разделах. В этом разделе мы подробно остановимся на использовании правил Кирхгофа для анализа более сложных схем. Например, схема на рис. 6.3.1 известна как многоконтурная схема , состоящая из разветвлений. Соединение, также известное как узел, представляет собой соединение трех или более проводов.
В этой схеме нельзя использовать предыдущие методы, потому что не все резисторы расположены последовательно или параллельно, и их можно уменьшить. Попробуйте. Резисторы и соединены последовательно и могут быть уменьшены до эквивалентного сопротивления. То же самое верно для резисторов и . Но что вы делаете тогда?
Несмотря на то, что эту цепь нельзя проанализировать с помощью уже изученных методов, для анализа любой цепи, простой или сложной, можно использовать два правила анализа цепей. Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).
(рис. 6.3.1)
Рисунок 6.3.1 Эта схема не может быть сведена к комбинации последовательного и параллельного соединений. Однако мы можем использовать правила Кирхгофа для его анализа.
ПРАВИЛА КИРХГОФА
- Первое правило Кирхгофа — правило соединения . Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения:
(6.
3.1) - Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю:
(6.3.2)
3.1) Теперь мы даем объяснения этих двух правил, за которыми следуют советы по решению проблем по их применению и рабочий пример, в котором они используются.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения) применяется к заряду, входящему в соединение и выходящему из него (рис. 6.3.2). Как указывалось ранее, узел или узел — это соединение трех или более проводов. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу.
(рис. 6.3.2)
Рисунок 6.3.2 Заряд должен сохраняться, поэтому сумма токов, поступающих в соединение, должна быть равна сумме токов, вытекающих из соединения.
Хотя это упрощение, можно провести аналогию с водопроводными трубами, соединенными в сантехническом узле.
Если провода на Рисунке 6.3.2 были заменены водопроводными трубами, а вода предполагалась несжимаемой, объем воды, втекающей в соединение, должен быть равен объему воды, вытекающей из соединения.
Второе правило Кирхгофа
Второе правило Кирхгофа ( петлевое правило ) применяется к разности потенциалов. Правило цикла сформулировано в терминах потенциальной, а не потенциальной энергии, но они связаны, поскольку . В замкнутом контуре, какая бы энергия ни поставлялась источником напряжения, энергия должна передаваться в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в цепь или из нее. Правило петли Кирхгофа гласит, что алгебраическая сумма разностей потенциалов, включая напряжения, подаваемые источниками напряжения и резистивными элементами, в любой петле должна быть равна нулю. Например, рассмотрим простую петлю без соединений, как на рисунке 6.3.3.
(рис. 6.3.3)
Рисунок 6.3.3 Простая петля без соединений.
Правило цикла Кирхгофа гласит, что алгебраическая сумма разностей напряжений равна нулю.
Схема состоит из источника напряжения и трех внешних нагрузочных резисторов. Ярлыки , , , и служат ссылками и не имеют никакого другого значения. Полезность этих ярлыков скоро станет очевидной. Петля обозначена как Loop , а метки помогают отслеживать разность напряжений, когда мы перемещаемся по цепи. Начните с точки и двигайтесь к ней. К уравнению добавляется напряжение источника напряжения и вычитается падение потенциала на резисторе. От точки до вычитается падение потенциала. От до вычитается падение потенциала. От точек до ничего не делается, потому что нет компонентов.
На рис. 6.3.4 показан график изменения напряжения при перемещении по контуру. Напряжение увеличивается, когда мы пересекаем батарею, тогда как напряжение уменьшается, когда мы пересекаем резистор. Падение потенциала или изменение электрического потенциала равно току через резистор, умноженному на сопротивление резистора.
Поскольку провода имеют незначительное сопротивление, напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
(рис. 6.3.4)
Рисунок 6.3.4 График напряжения при перемещении по цепи. Напряжение увеличивается, когда мы пересекаем батарею, и уменьшается, когда мы пересекаем каждый резистор. Поскольку сопротивление провода довольно мало, мы предполагаем, что напряжение остается постоянным, когда мы пересекаем провода, соединяющие компоненты.
Тогда правило цикла Кирхгофа утверждает
Уравнение контура можно использовать для определения тока через контур:
Эту петлю можно было бы проанализировать с помощью предыдущих методов, но мы продемонстрируем возможности метода Кирхгофа в следующем разделе.
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем набор линейных уравнений, которые позволяют нам находить неизвестные значения в цепях. Это могут быть токи, напряжения или сопротивления.
Каждый раз, когда правило применяется, оно создает уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема.
Использование метода анализа Кирхгофа требует выполнения нескольких шагов, перечисленных в следующей процедуре.
Стратегия решения проблем: правила Кирхгофа
- Обозначьте точки на электрической схеме строчными буквами. Эти метки просто помогают с ориентацией.
- Найдите соединения в цепи. Соединения — это точки, в которых соединяются три или более проводов. Обозначьте каждое соединение токами и направлениями в него и из него. Убедитесь, что по крайней мере один ток указывает на соединение и по крайней мере один ток указывает на соединение.
- Выберите петли в цепи. Каждый компонент должен содержаться по крайней мере в одном цикле, но компонент может содержаться более чем в одном цикле.
- Применить правило соединения. Опять же, некоторые соединения не должны быть включены в анализ. Вам нужно только использовать достаточное количество узлов, чтобы включить каждый текущий.
- Применить правило цикла. Используйте карту на рисунке 6.3.5.
Вам нужно только использовать достаточное количество узлов, чтобы включить каждый текущий. (рис. 6.3.5)
Рисунок 6.3.5 Каждый из этих резисторов и источников напряжения проходит от до . (a) При перемещении через резистор в том же направлении, что и ток, вычтите падение потенциала. (b) При перемещении через резистор в направлении, противоположном течению тока, добавьте падение потенциала. (c) При перемещении через источник напряжения от отрицательной клеммы к положительной клемме добавьте падение потенциала. (d) При перемещении через источник напряжения от положительной клеммы к отрицательной клемме вычтите падение потенциала.
Рассмотрим некоторые шаги этой процедуры более подробно. При нахождении соединений в цепи не беспокойтесь о направлении токов. Если направление протекания тока неочевидно, достаточно выбрать любое направление, если по крайней мере один ток указывает на соединение, а по крайней мере один ток направлен из соединения.
Если стрелка находится в направлении, противоположном обычному течению тока, результат для рассматриваемого тока будет отрицательным, но ответ все равно будет правильным.
Количество узлов зависит от схемы. Каждый ток должен быть включен в узел и, таким образом, включен по крайней мере в одно уравнение соединения. Не включайте узлы, которые не являются линейно независимыми, то есть узлы, содержащие одинаковую информацию.
См. рис. 6.3.6. В этой цепи есть два соединения: соединение и соединение . Точки , , и не являются соединениями, потому что соединение должно иметь три или более соединения. Уравнение для соединения , а уравнение для соединения . Это эквивалентные уравнения, поэтому необходимо оставить только одно из них.
(рис. 6.3.6)
Рисунок 6.3.6 На первый взгляд, эта схема содержит два соединения, Соединение и Соединение , но следует рассматривать только одно, поскольку их уравнения соединения эквивалентны.
При выборе петель в схеме необходимо столько петель, чтобы каждый компонент был покрыт один раз, без повторения петель.
На рис. 6.3.7 показаны четыре варианта циклов для решения примера схемы; варианты (a), (b) и (c) имеют достаточное количество циклов, чтобы полностью решить схему. Вариант (г) отражает больше циклов, чем необходимо для решения схемы.
(рис. 6.3.7)
Рисунок 6.3.7 Панели (a)–(c) достаточны для анализа цепи. В каждом случае две показанные петли содержат все элементы схемы, необходимые для полного решения схемы. На панели (d) показаны три использованные петли, что больше, чем необходимо. Любые два цикла в системе будут содержать всю информацию, необходимую для решения схемы. Добавление третьего цикла обеспечивает избыточную информацию.
Рассмотрим схему на рис. 6.3.8(a). Давайте проанализируем эту схему, чтобы найти ток через каждый резистор. Сначала пометьте схему, как показано в части (b).
(рис. 6.3.8)
Рисунок 6.3.8 (a) Многоконтурная схема. (b) Подпишите схему, чтобы помочь с ориентацией.
Далее определите развязки.
В этой схеме точки и соединены по три провода, что делает их соединениями. Начните применять правило соединения Кирхгофа, нарисовав стрелки, представляющие токи, и пометив каждую стрелку, как показано на рисунке 6.3.9 (b). Junction показывает это, а Junction показывает это. Поскольку Junction предоставляет ту же информацию, что и Junction , ею можно пренебречь. В этой схеме три неизвестных, поэтому для ее анализа нам нужны три линейно независимых уравнения.
(рис. 6.3.9)
Рисунок 6.3.9 (a) Эта схема имеет два соединения, обозначенных b и e, но в анализе используется только узел b. (б) Маркированные стрелки представляют токи в и из соединений.
Далее нам нужно выбрать петли. На рис. 6.3.10 контур включает в себя источник напряжения, резисторы и . Цикл начинается с точки , затем проходит через точки , , и , а затем возвращается к точке . Второй контур, Loop , начинается в точке и включает резисторы и и источник напряжения .
(рис. 6.3.
10)
Рисунок 6.3.10 Выберите петли в цепи.
Теперь мы можем применить правило цикла Кирхгофа, используя карту на Рисунке 6.3.5. Начиная с точки и двигаясь к точке, сопротивление пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается. Перемещаясь от точки к точке, резистор пересекается в том же направлении, что и ток, поэтому падение потенциала вычитается. При переходе от точки к точке источник напряжения пересекается с отрицательной клеммы на положительную, поэтому добавляется . Между точками и 9 нет компонентов0011 . Сумма разностей напряжений должна быть равна нулю:
Наконец, мы проверяем цикл. Мы начинаем с точки и движемся к ней, пересекая ее в направлении, противоположном текущему потоку. Потенциальное падение добавлено. Затем мы пересекаем и в том же направлении, что и текущий поток , и вычитаем падения потенциала и . Обратите внимание, что ток через резисторы и одинаков, поскольку они соединены последовательно.
Наконец, источник напряжения пересекается с положительной клеммы на отрицательную клемму, и источник напряжения вычитается. Сумма этих разностей напряжений равна нулю и дает уравнение контура
Теперь у нас есть три уравнения, которые мы можем решить для трех неизвестных.
Чтобы решить три уравнения для трех неизвестных токов, начните с исключения тока . Сначала добавьте уравнение (1) раз к уравнению (2). Результат помечен как уравнение. (4):
Затем вычтите уравнение (3) из уравнения (2). Результат помечен как уравнение. (5):
Мы можем решить уравнения. (4) и (5) для тока . Складывая семь раз уравнение (4) и трижды уравнение. (5) приводит к , или . Используя уравнение (4) приводит к . Наконец, уравнение (1) дает . Один из способов проверить согласованность решений — проверить мощность, подаваемую источниками напряжения, и мощность, рассеиваемую резисторами:
Обратите внимание, что решение для текущего отрицательно.
Это правильный ответ, но он предполагает, что стрелка, первоначально нарисованная при анализе соединения, указывает направление, противоположное обычному протеканию тока. Мощность, подаваемая вторым источником напряжения, равна и не равна .
ПРИМЕР 6.3.1
Расчет силы тока с помощью правил Кирхгофа
Найдите токи, протекающие в цепи на рисунке 6.3.11.
(рис. 6.3.11)
Рисунок 6.3.11 Эта схема представляет собой комбинацию последовательных и параллельных конфигураций резисторов и источников напряжения. Эту цепь нельзя проанализировать с помощью методов, описанных в разделе «Электродвижущая сила», но ее можно проанализировать с помощью правил Кирхгофа.
Стратегия
Эта цепь настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Течения обозначены на рисунке , и , и сделаны предположения об их направлениях. Места на схеме обозначены буквами от до .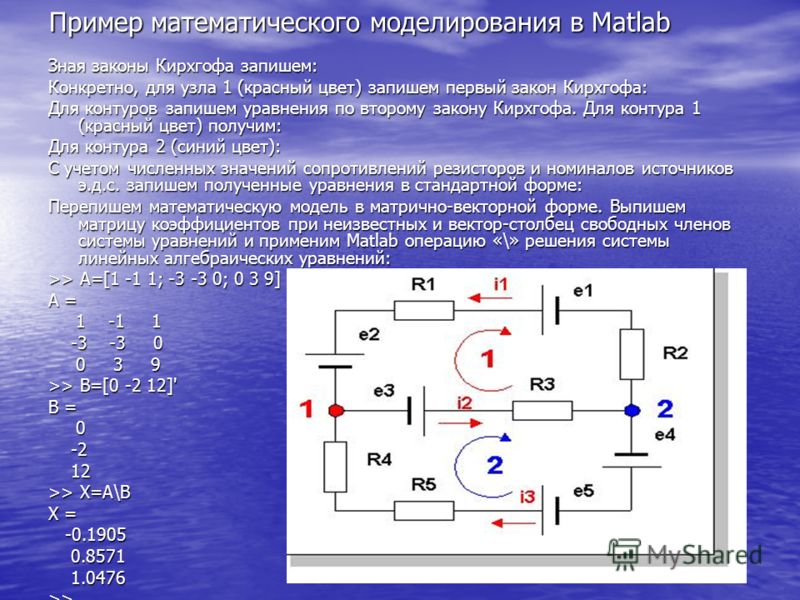
В решении мы применяем правила соединения и петли, ищем три независимых уравнения, которые позволяют нам найти три неизвестных тока.
Решение
Применение правил соединения и петли приводит к следующим трем уравнениям. У нас есть три неизвестных, поэтому требуется три уравнения.
Упростите уравнения, поместив неизвестные в одну сторону уравнений.
Упростите уравнения. Первое уравнение контура можно упростить, разделив обе части на . Второе уравнение цикла можно упростить, разделив обе части на .
Результат:
Значение
Метод проверки расчетов заключается в вычислении мощности, рассеиваемой резисторами, и мощности, выдаваемой источниками напряжения:
Подводимая мощность равна мощности, рассеиваемой резисторами.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 6.
6
При рассмотрении следующей схемы и мощности, подаваемой и потребляемой цепью, будет ли источник напряжения всегда обеспечивать питание цепи или источник напряжения может потреблять энергию?
ПРИМЕР 6.3.2
Расчет силы тока с помощью правил Кирхгофа
Найдите ток, протекающий в цепи на рисунке 6.3.12.
(рис. 6.3.12)
Рисунок 6.3.12 Эта схема состоит из трех резисторов и двух батарей, соединенных последовательно. Обратите внимание, что батареи подключены с противоположной полярностью.
Стратегия
Эту схему можно проанализировать с помощью правил Кирхгофа. Есть только одна петля и нет узлов. Выберите направление тока. В этом примере мы будем использовать направление по часовой стрелке от точки к точке . Рассмотрите цикл и используйте рисунок 6.3.5, чтобы написать уравнение цикла. Обратите внимание, что согласно рисунку 6.3.5 батарея будет добавлена, а батарея вычтена.
Решение
Применение правила соединения приводит к следующим трем уравнениям.
У нас есть одно неизвестное, поэтому требуется одно уравнение:
Упростите уравнения, поместив неизвестные в одну сторону уравнений. Используйте значения, указанные на рисунке.
Значение
Мощность, рассеиваемая или потребляемая цепью, равна мощности, подаваемой в цепь, но обратите внимание, что ток в батарее протекает через батарею от положительной клеммы к отрицательной клемме и потребляет энергию.
Подводимая мощность равна мощности, рассеиваемой резисторами и потребляемой батареей.
ПРОВЕРЬТЕ ВАШЕ ПОНИМАНИЕ 6.7
При использовании законов Кирхгофа необходимо решить, какие контуры использовать и направление тока через каждый контур. При анализе схемы в примере 6.3.2 направление тока было выбрано по часовой стрелке, от точки a до точки b . Как изменились бы результаты, если бы направление тока было выбрано против часовой стрелки, от точки к точке?
Несколько источников напряжения
Для многих устройств требуется более одной батареи.
Несколько источников напряжения, таких как батареи, могут быть соединены последовательно, параллельно или в комбинации.
Последовательно положительная клемма одной батареи подключается к отрицательной клемме другой батареи. Любое количество источников напряжения, включая батареи, может быть соединено последовательно. Две батареи, соединенные последовательно, показаны на рисунке 6.3.13. Использование правила цикла Кирхгофа для схемы в части (b) дает результат
(рис. 6.3.13)
Рисунок 6.3.13 (a) Две батареи, соединенные последовательно с нагрузочным резистором. (b) Принципиальная схема двух батарей и нагрузочного резистора, где каждая батарея моделируется как идеализированный источник ЭДС и внутреннее сопротивление.
Когда источники напряжения соединены последовательно, их внутренние сопротивления могут быть сложены вместе, а их ЭДС могут быть сложены вместе, чтобы получить общие значения. Распространены последовательные соединения источников напряжения, например в фонарях, игрушках и др.
приборах. Обычно ячейки соединяют последовательно для получения большей общей ЭДС. На рисунке 6.3.13 напряжение на клеммах равно
Обратите внимание, что в каждой батарее присутствует одинаковый ток, поскольку они соединены последовательно. Недостатком последовательного соединения ячеек является аддитивность их внутренних сопротивлений.
Батареи соединены последовательно для увеличения напряжения, подаваемого в цепь. Например, светодиодный фонарик может иметь две батарейки типа ААА, каждая с напряжением на клеммах 10 000 000 000 ₽, чтобы питать фонарик.
Последовательно можно соединить любое количество аккумуляторов. Для батарей, соединенных последовательно, напряжение на клеммах равно
(6.3.3)
, где эквивалентное сопротивление равно .
Когда нагрузка подключена к источникам напряжения последовательно, как показано на рисунке 6.3.14, мы можем найти ток:
Как и ожидалось, внутренние сопротивления увеличивают эквивалентное сопротивление.
(рис. 6.3.14)
Рисунок 6.3.14 Две батареи соединены последовательно со светодиодной лампочкой, как в фонарике.
Источники напряжения, такие как батареи, также могут быть подключены параллельно. На рис. 6.3.15 показаны две батареи с одинаковыми ЭДС, подключенные параллельно и подключенные к сопротивлению нагрузки. Когда батареи соединены параллельно, положительные клеммы соединены вместе, а отрицательные клеммы соединены вместе, а сопротивление нагрузки подключено к положительной и отрицательной клеммам. Обычно параллельно подключенные источники напряжения имеют одинаковые ЭДС. В этом простом случае, поскольку источники напряжения параллельны, общая ЭДС такая же, как и отдельные ЭДС каждой батареи.
(рис. 6.3.15)
Рисунок 6.3.15 (a) Две батареи подключены параллельно к нагрузочному резистору. (b) На принципиальной схеме показана батарея в качестве источника ЭДС и внутреннего резистора. Два источника ЭДС имеют одинаковые ЭДС (каждый из которых помечен ), соединенные параллельно, которые производят одинаковую ЭДС.
Рассмотрим анализ Кирхгофа схемы на рис. 6.3.15(b). В точках и есть две петли и узел.
Решение для тока через нагрузочный резистор дает , где . Напряжение на клеммах равно падению потенциала на нагрузочном резисторе. Параллельное соединение снижает внутреннее сопротивление и, таким образом, может производить больший ток.
Параллельно можно соединить любое количество аккумуляторов. Для батарей, соединенных параллельно, напряжение на клеммах равно
В.
(6.3.4)
, где эквивалентное сопротивление равно .
Например, некоторые дизельные грузовики используют две батареи параллельно; они производят общую ЭДС, но могут обеспечить больший ток, необходимый для запуска дизельного двигателя.
Таким образом, напряжение на клеммах последовательно соединенных батарей равно сумме индивидуальных ЭДС минус сумма внутренних сопротивлений, умноженная на ток. Когда батареи соединены параллельно, они обычно имеют одинаковую ЭДС, а напряжение на клеммах равно ЭДС минус эквивалентное внутреннее сопротивление, умноженное на ток, где эквивалентное внутреннее сопротивление меньше отдельных внутренних сопротивлений.
Батареи соединены последовательно, чтобы увеличить напряжение на клеммах нагрузки. Батареи соединены параллельно для увеличения тока нагрузки.
Солнечные батареи
Другим примером, связанным с несколькими источниками напряжения, является комбинация солнечных элементов , соединенных как последовательно, так и параллельно для получения желаемого напряжения и тока. Фотоэлектрическая генерация, которая представляет собой преобразование солнечного света непосредственно в электричество, основана на фотоэлектрическом эффекте. Фотоэлектрический эффект выходит за рамки этого учебника, но, как правило, фотоны, ударяясь о поверхность солнечного элемента, создают электрический ток в элементе.
Большинство солнечных элементов сделаны из чистого кремния. Большинство отдельных ячеек имеют выходное напряжение около 100 мА, а выходной ток зависит от количества солнечного света, падающего на ячейку (падающее солнечное излучение, известное как инсоляция). При ярком полуденном солнечном свете типичные монокристаллические клетки производят ток на единицу площади, составляющий около площади поверхности клетки.
Добавить комментарий