Поток вектора магнитной индукции в чем измеряется: Поток вектора магнитной индукции

Поток вектора магнитной индукции

Определение 1

Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:

Φ=BScos α=BnS=B→S→ с углом между n→ и B→, обозначаемым α, n→ является нормалью к площадке S.

Формула магнитного потока

Φ равняется количеству линий магнитной индукции, пересекающих площадку S, как показано на рисунке 1. Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S. Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.

Рисунок 1

В чем измеряется магнитный поток

В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки dS, рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока dΦ производится через эту поверхность. Запись примет вид:

dΦ=BdScos α=B→dS→.

Нахождение полного потока через поверхность S:

Φ=∫SBdScos α=∫SB→dS→.

Основной единицей измерения магнитного потока в системе СИ считаются веберы (Вб). 1 Вб=1 Тл1 м2.

Связь магнитного потока и работы сил магнитного поля

Элементарная работа δA, совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции dΦ:

δA=IdΦ.

Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:

A=IΦ2-Φ1 с Φ1, обозначаемым потоком через контур в начале перемещения, Φ2 является  потоком через контур в конце перемещения.

Теорема Гаусса для магнитного поля

Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:

∮B→dS→=0.

Выражение ∮B→dS→=0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:

∮E→dS→=qε0.

Запись ∮B→dS→=0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.

Пример 1

Дан бесконечно длинный прямой проводник с током I, недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I’. Сторона рамки равна a. Она располагается в одной плоскости с проводом, как показано на рисунке 2. Значение расстояния от ближайшей стороны рамки до проводника равняется b. Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

Рисунок 2

Решение

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.

Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.

За основу возьмем формулу магнитного потока и работы, которая их связывает:

A=I’Φ2-Φ1 (1.1), где I’ принимают за силу тока в рамке, Φ1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b. Φ2=0. Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы (1.1) изменится:

A=-I’Φ1 (1.2).

Перейдем к нормали n→ и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n→ и вектором B→ равняется π. Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:

dΦ=-BdS=-B·a·dx=-μ02πIldxx (1.3), значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:

B=μ02πxIl (1.4).

Отсюда следует, что для нахождения всего потока из (1.3) потребуется:

Φ1=∫S-μ02πIldxx=-μ02πIl∫bb+adxx=-μ02πIl·lnb+ab (1.5).

Произведем подстановку формулы (1.5) в (1.2). Искомая работа равняется:

A=I’μ02πIl·lnb+ab.

Ответ: A=μ02πII’l·lnb+ab.

Пример 2

Найти силу, действующую на рамку, из предыдущего примера.

Решение

Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние dx. Это говорит о совершении силой работы, равной:

δA=Fdx (2.1).

Элементарная работа δA может быть выражена как:

δA=I’dΦ (2.2).

Произведем то же с силой, применяя формулы (2.1), (2.2). Получаем:

Fdx=I’dΦ→F=I’dΦdx (2.3).

Используем выражение, которое было получено в примере 1:

dΦ=-μ02πIldxx→dΦdx=-μ02πIlx (2.4).

Произведем подстановку dΦdx в (2.3). Имеем:

F=I’μ02πIlx (2.5).

Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны AB и DC равные по модулю и противоположные по направлению. Выражение принимает вид:

FAB→+FDC→=0 (2.6), то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:

F→=FAD→+FBC→ (2. 6).

Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:

F=FAD-FBC (2.7).

Произведем поиск силы FAD, действующей на сторону AD, применив формулу (2.5), где x=b:

FAD=I’м02πIlb (2.8).

Значение FBC будет:

FBC=I’μ02πIlb+a (2.9).

Для нахождения искомой силы:

F=I’μ02πIlb-I’μ02πIlb+a=II’μ0l2π1b-1b+a.

Ответ: F=II’μ0l2π1b-1b+a. Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.

Автор:
Роман Адамчук

Преподаватель физики

Навигация по статьям

Предыдущая статья

Основные интерференционные схемы

Следующая статья

Вихревой характер магнитного поля

• Вихревой характер магнитного поля
• Закон Био-Савара. Теорема о циркуляции
• Закон электромагнитной индукции Фарадея
• Классификация магнетиков
• Классическое описание диамагнетизма
• Все темы по физике

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Все предметы

Узнать подробнее

сестринская и паллиативная помощь детям при лейкозе

• Вид работы:

  Курсовая работа

• Выполнена:

  10 мая 2022 г.

• Стоимость:

  1 900 руб

Заказать такую же работу

Картографирование учебных атласов

• Вид работы:

  Курсовая работа

• Выполнена:

  19 апреля 2022 г.

• Стоимость:

  2 400 руб

Заказать такую же работу

тема пчеловодство все о пчелах

• Вид работы:

  Школьный проект

• Выполнена:

  12 апреля 2022 г.

• Стоимость:

  1 400 руб

Заказать такую же работу

решить задачи шт

• Вид работы:

  Домашняя работа

• Выполнена:

  22 сентября 2021 г.

• Стоимость:

  600 руб

Заказать такую же работу

Проект установки очистки дымовых газов от диоксида серы

Заказать такую же работу

выполнить все задания в файле

• Вид работы:

  Контрольная работа

• Выполнена:

  2 мая 2021 г.

• Стоимость:

  1 800 руб

Заказать такую же работу

Смотреть все работы по сестринскому делу

Электричество и магнетизм

Потоком вектора магнитной индукции В (магнитным потоком) через малую поверхность площадью dS называется скалярная физическая величина, равная               (6. 26)

Здесь ,  — единичный вектор нормали к площадке площадью dS, В_n — проекция вектора В  на направление нормали,  — угол между векторами В и n (рис. 6.28).

 

Рис. 6.28. Поток вектора магнитной индукции через площадку 

Магнитный поток Ф_B  через произвольную замкнутую поверхность S равен

(6.27)

Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В  не имеют ни начала, ни конца. Поэтому поток вектора В  через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S выполняется условие

(6.28)

Формула (6.28) выражает теорему Остроградского — Гаусса для вектора :  

Поток вектора магнитной индукции через произвольную замкнутую поверхность тождественно равен нулю.

 

Подчеркнем еще раз: эта теорема является математическим выражением того факта, что в природе отсутствуют магнитные заряды, на которых начинались бы и заканчивались линии магнитной индукции, как это имело место в случае напряженности электрического поля Е  точечных зарядов.

Это свойство существенным образом отличает магнитное поле от электрического. Линии магнитной индукции замкнуты, поэтому число линий, входящих в некоторый объем пространства, равно числу линий, выходящих из этого объема. Если входящие потоки брать с одним знаком, а выходящие — с другим, то суммарный поток вектора магнитной индукции через замкнутую поверхность будет равен нулю. 

В системе СИ единицей измерения магнитного потока является вебер (Вб) (рис. 6.29):

 

Рис. 6.29. В. Вебер (1804–1891) — немецкий физик 

Отличие магнитного поля от электростатического проявляется также в значении величины, которую мы называем циркуляцией — интеграла от векторного поля по замкнутому пути. В электростатике равен нулю интеграл

взятый по произвольному замкнутому контуру. Это связано с потенциальностью электростатического поля, то есть с тем фактом, что работа по перемещению заряда в электростатическом поле не зависит от пути, но лишь от положения начальной и конечной точек.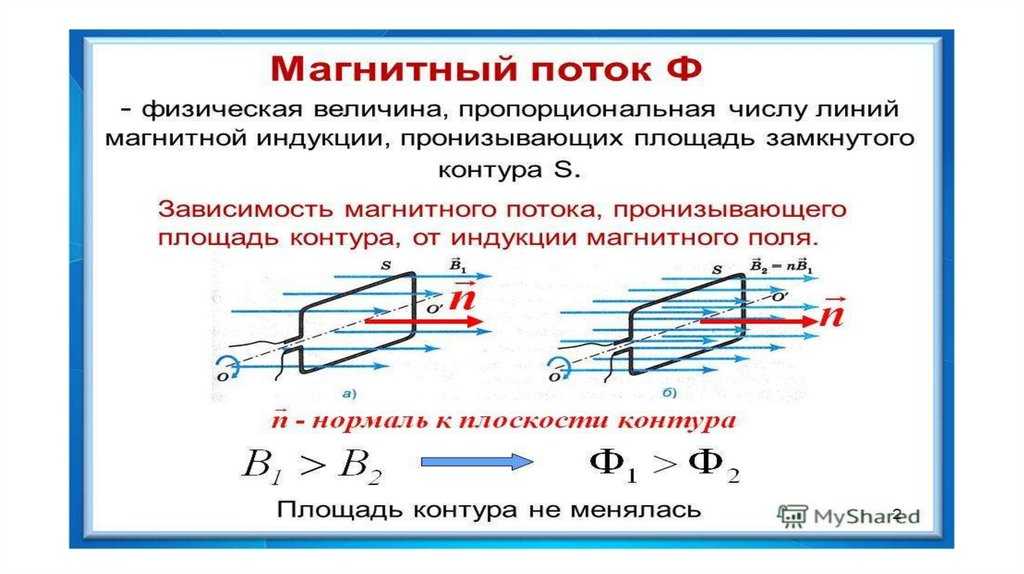

Посмотрим, как обстоит дело с аналогичной величиной для магнитного поля. Возьмем замкнутый контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора В, то есть

 

Как было получено выше, магнитная индукция, создаваемая прямолинейным проводником с током на расстоянии R от проводника, равна

Рассмотрим случай, когда контур, охватывающий прямой ток, лежит в плоскости, перпендикулярной току, и представляет собой окружность радиусом R с центром на проводнике. В этом случае циркуляция вектора В  по этой окружности равна

(6.29)

откуда

(6.30)

Можно показать, что результат для циркуляции вектора магнитной индукции не меняется при непрерывной деформации контура, если при этой деформации контур не пересекает линий тока. Тогда в силу принципа суперпозиции циркуляция вектора магнитной индукции по пути, охватывающем несколько токов, пропорциональна их алгебраической сумме (рис. 6.30)

(6.31)

Рис. 6.30. Замкнутый контур (L) с заданным направлением обхода.

Изображены токи I₁, I₂ и I₃, создающие магнитное поле.

Вклад в циркуляцию магнитного поля вдоль контура (L) дают только токи  I₂ и I₃

Если выбранный контур не охватывает токов, то циркуляция  по нему равна нулю. 

При вычислении алгебраической суммы токов следует учитывать знак тока: положительным будем считать ток, направление которого связано с направлением обхода по контуру правилом правого винта. Например, вклад тока I₂ в циркуляцию — отрицательный, а вклад тока I₃ — положительный (рис. 6.18). Воспользовавшись соотношением

между силой тока I через любую замкнутую поверхность S и плотностью тока , для циркуляции вектора В можно записать

(6.32)

где S — любая замкнутая поверхность, опирающаяся на данный контур L. 

Итак,  

Циркуляция магнитной индукции отлична от нуля, если контур, по которому она берется, охватывает ток.

 

Такие поля называются вихревыми. Поэтому для магнитного поля нельзя ввести потенциал, как это было сделано для электрического поля точечных зарядов. Наиболее наглядно разницу потенциального и вихревого полей можно представить по картине силовых линий. Силовые линии электростатического поля похожи на ежей: они начинаются и кончаются на зарядах (либо уходят в бесконечность). Силовые линии магнитного поля никогда не напоминают «ежей»: они всегда замкнуты и охватывают текущие токи. 

Для иллюстрации применения теоремы о циркуляции найдем другим методом уже известное нам магнитное поле бесконечного соленоида. Возьмем прямоугольный контур 1-2-3-4 (рис. 6.31) и вычислим циркуляцию вектора В по этому контуру

(6.33)

Рис. 6.31. Применение теоремы о циркуляции В к определению магнитного поля соленоида 

Второй и четвертый интегралы равны нулю в силу перпендикулярности векторов  и . Третий интеграл можно положить равным нулю, ввиду малости магнитного поля вне соленоида. Поэтому

(6. 34)

Рассмотренный контур охватывает суммарный ток nlI, где n — число витков соленоида, приходящееся на единицу длины, I — сила тока в соленоиде. Следовательно,

или

 

(6.35)

Мы воспроизвели результат (6.20) без интегрирования магнитных полей от отдельных витков. 

Полученный результат (6.35) можно использовать для нахождения магнитного поля тонкого тороидального соленоида (рис.6.32).  

 

Рис. 6.32. Тороидальная катушка: линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r₁ ≤ r < r₂ изображена на рисунке

 

Дополнительная информация 

http://www. magnet.fsu.edu/education/tutorials/pioneers/weber.html — Вильгельм Вебер (1804–1891).

Магнитная индукция (B) и поток (F). Объяснение закона Фарадея

EEE Компоненты ПАССИВНЫЕ

Магнитная индукция B

Потенциал индуцируется в петле проводника, если магнитное поле, проходящее через петлю проводника, изменяется со временем.

Рекомендуемое изображение Рис. 1.10: Экспериментальная конфигурация для магнитной индукции

Всплеск потенциала на площади контура известен как магнитная индукция B. Как и напряженность магнитного поля, магнитная индукция B является векторной величиной.

Для магнитной индукции B применяется следующее соотношение:

Магнитная индукция (B) представляет собой частное индуцированного скачка напряжения:

и произведение витков обмотки (N) и площади обмотки ( А) индукционной катушки.

Единицей магнитной индукции (В) является Тесла (Тл) = Вс/м2.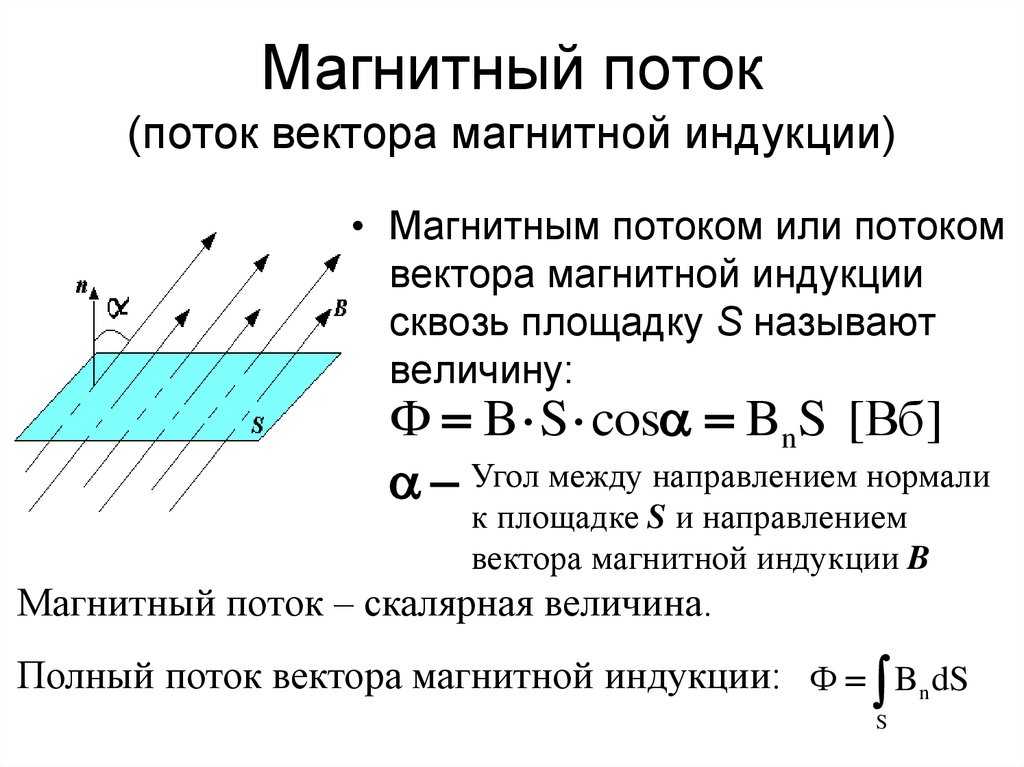

Магнитная индукция B и напряженность поля H пропорциональны друг другу.

Константа пропорциональности – это постоянная магнитного поля (µ0), полученная экспериментальным путем.

В вакууме, а также с достаточной точностью для воздуха это приводит к:

Магнитная индукция (BL) в воздухе для приведенного выше примера определяется как:

Магнитный поток F

Магнитный поток (F ) представляет собой скалярное произведение плотности магнитного потока (B) и вектора площади (dA).

Если (B) проходит через площадь перпендикулярно и поле однородно:

Единица измерения магнитного потока (F) такая же, как и у скачка напряжения (Vs) (Вольт-секунда) или Вебера (Вб).

Закон Фарадея

До сих пор мы рассматривали статические магнитные поля. Если магнитный поток изменяется со временем, индуцируется напряжение U (закон Фарадея).

U = индуцированное напряжение
t = время

Полярность напряжения такова, что при замыкании цепи возникает ток, индуцированное магнитное поле которого противодействует исходному магнитному потоку, т. е. стремится уменьшить магнитное поле (правило Ленца – Фигура).

Рисунок : Представление правила Ленца. Наложенное магнитное поле индуцирует ток в таком направлении, что его индуцированное магнитное поле противодействует наложенному полю

Взяв обмотку с N витками, закон Фарадея можно выразить в следующем виде.

A = поперечное сечение катушки
l = длина катушки или магнитной цепи
I = ток через катушку
L = индуктивность катушки [H(enry) = Vs/A]

Итак, индуктивность ограничивает изменение тока после подачи напряжения. Его можно рассчитать по данным катушки:

AL = значение AL; в основном в нГн/N2

Энергия, запасенная в магнитном поле, подчиняется следующим соотношениям:

Энергия, хранящаяся в объеме V, состоит как из напряженности магнитного поля H, так и из плотности магнитного потока B. Для трансформаторов и дросселей с ферромагнитными сердечниками плотность потока ограничена насыщением (см. главу I/1. 5) и постоянна на всем протяжении магнитная цепь. Если вводится воздушный зазор (материал с проницаемостью µ~1), то напряженность поля в этом воздушном зазоре максимальна с H = B/µ. Отсюда следует, что плотность энергии наибольшая в воздушном зазоре. Также говорят об энергии, хранящейся в воздушном зазоре.

При сравнении магнитных полей с электрическими обнаруживаются аналогии между некоторыми параметрами. Они приведены в таблице ниже:

Таб. :  Аналогии между магнитными и электрическими полями

• Автор
• Последние сообщения

Томаш Зедничек

Основатель и президент ЕВРОПЕЙСКОГО ИНСТИТУТА ПАССИВНЫХ КОМПОНЕНТОВ ( EPCI)
ЭПКИ | Объединение пассивных профессионалов

Степень в области электротехники, Технический университет Брно, Чехия, 1993 г.
Кандидат технических наук. в танталовых конденсаторах в 2000 г.
> 21 год работы в компании-производителе танталовых конденсаторов
> 15 лет в должности менеджера по техническому маркетингу по всему миру
более 60 технических документов и 1 американский/международный патент
4 выдающихся/лучших технических документа в CARTS пассивный компонент конференция
2005 Награда доктора Зандмана за большой вклад в индустрию пассивных компонентов
Преподаватель конденсаторных технологий, навыков презентации и межкультурной коммуникации
Июль 2015 г. – Основатель Европейского института пассивных компонентов

Последние сообщения Томаша Зедничка (см. все)

0
0
голосов

Рейтинг статьи

Предыдущий пост

Емкость, диполи и диэлектрическое поглощение

Следующий пост

Импульсная нагрузка, снижение мощности и напряжения на резисторах

Разница между измерением магнитного потока и магнитных полей

Проще говоря, магнитное поле аналогично электрическому напряжению, а магнитный поток аналогичен электрическому току. Магнитная цепь аналогична электрической цепи с важными отличиями. Электродвижущая сила в электрической цепи соответствует магнитодвижущей силе. Сопротивление и его обратная проводимость в электрической цепи соответствуют сопротивлению и его обратной проводимости в магнитной цепи. Но есть тонкие способы, в которых силы соотносятся лишь приблизительно, а сравнения несовершенны.

Другими словами, напряженность магнитного поля (H в амперах на метр) представляет собой величину намагничивающей силы. Эта сила прямо пропорциональна току, переносимому по проводнику, и длине проводника. Плотность магнитного потока (B в Тесла или Вебер/м ² ) представляет собой величину магнитной силы, индуцируемой на данном теле из-за намагничивающей силы H. Величина индуцируемой магнитной силы зависит от силы H и природы магнитного поля. середина.

Намагниченное тело имеет северный и южный полюса, и эти полюса всегда существуют связанными парами. Если вы разрежете стержневой магнит пополам, чтобы сделать два более коротких стержневых магнита, каждый из новых магнитов будет иметь северный и южный полюса. Магнитный монополь так и не был обнаружен.

Железные опилки образуют магнитомагнитные силовые линии.

Магнитное поле, связанное с постоянным магнитом, можно продемонстрировать, поместив лист бумаги над магнитом и случайным образом посыпав бумагу железными опилками. Каждая частица быстро намагничивается своими северным и южным полюсами, и поскольку их противоположные полюса притягиваются, они образуют линии, представляющие магнитное поле. Плотность линий (количество линий на миллиметр) и направление линий показывают, что магнитное поле является векторным полем. Линии меняют направление и становятся ближе или дальше друг от друга по мере изменения плотности поля.

Железные опилки могут показывать направление и напряженность магнитного поля, но не являются векторным полем. Они подобны следам на песке или ряби в движущемся потоке, а не настоящей воде. B и H пропорциональны в вакууме, но расходятся внутри магнитных материалов. Намагниченность, обозначаемая буквой M в верхнем регистре, является мерой степени, в которой материалы реагируют на приложенное поле B. Диамагнетики создают намагниченность, противодействующую приложенному полю. Парамагнетики создают намагниченность в том же направлении, что и приложенное поле.

В обоих случаях М обычно пропорциональна приложенному магнитному полю. Связь между B и H такова: B = µH, где µ — проницаемость среды, через которую проходит поток. Проницаемость различается для разных материалов и часто является гистерезисной, что означает, что она демонстрирует гистерезис в своей реакции на магнитные поля. Железо обладает высокой проницаемостью для магнитного потока.

Сначала количественно определяется магнитный поток путем создания воображаемой поверхности. Эта поверхность является строго математической конструкцией и может совпадать с поверхностью магнита или пересекаться с ней. Магнитный поток — это измерение величины потока, протекающего через поверхность. В частности, это большее количество линий, проходящих через поверхность в одном направлении, минус небольшое количество линий, проходящих через поверхность в противоположном направлении, или ноль, если они равны.

Соответствующее уравнение для плотности магнитного потока Φ имеет вид Φ = BA cosθ. А представляет собой площадь поверхности. Если поверхность перпендикулярна магнитному полю, cosθ = 1. Если поверхность расположена под углом к ​​силовым линиям, cosθ меньше единицы. Единицей магнитного потока в системе СИ является Вебер. Плотность потока представляет собой деление магнитного потока (векторно, если он направлен под углом) на площадь поверхности в единицах тесла.

Электрический ток в искусственных проводах протекает по изолированным проводникам. В магнитной области нет абсолютных изоляторов, но вместо этого все материалы обладают большим или меньшим сопротивлением, то есть меньшей или большей магнитной проницаемостью. Вот почему в эксперименте с железными опилками линии, представляющие магнитное поле, простираются далеко за пределы реального магнита. В двигателях, трансформаторах и подобных устройствах магнитный поток направляется через железные сердечники для выполнения желаемой работы.

Магнитный поток, движущийся через магнитную цепь под действием приложенной магнитодвижущей силы, выражается формулой F = ϕR, где F — магнитодвижущая сила всей или части магнитной цепи, ϕ — магнитный поток через данный сегмент, а R — магнитодвижущая сила. магнитное сопротивление сегмента.

Определяющее различие между электрической цепью и магнитодвижущей цепью заключается в том, что рассеиваемая мощность связана с сопротивлением, а не с сопротивлением. Электрическое поле заставляет ток следовать по пути наименьшего сопротивления, а магнитное поле заставляет магнитный поток следовать по пути наименьшего сопротивления.

Уравнения Максвелла утверждают, что магнитный поток всегда образует замкнутый контур. Магнитные цепи нелинейны. Сопротивление меняется в зависимости от магнитного поля. Когда магнитный поток превышает определенный уровень, проницаемый материал насыщается, поэтому не может быть дальнейшего увеличения величины потока, который ограничен неуправляемым сопротивлением. В резистивной электрической цепи такого явления не происходит.

Земной магнитометр в действии.

Типичным способом измерения магнитных полей является магнитометр. Векторные магнитометры измеряют векторные компоненты магнитного поля, тогда как магнитометры полного поля или скалярные магнитометры измеряют только величину векторного магнитного поля.

В магнитометрах используется несколько технологий. Обычный компас — это, по сути, простой магнитометр. Его стрелка измеряет направление поля. Частота колебаний намагниченной стрелки пропорциональна квадратному корню из напряженности окружающего магнитного поля.

Одной из самых простых магнитометрических технологий является индукционная измерительная катушка, которая измеряет намагниченность путем обнаружения тока, индуцируемого в катушке, вызванного изменением магнитного момента образца. Намагниченность образца можно изменить, приложив небольшое переменное магнитное поле (или быстро меняющееся постоянное поле), как в импульсных магнитах с конденсаторным приводом. Эти измерения требуют проведения различия между магнитным полем, создаваемым образцом, и внешним приложенным полем, часто с использованием катушек компенсации. Как правило, половина катушки датчика намотана в одном направлении, а другая половина — в другом. Образец сидит только в одной половине. Внешнее однородное магнитное поле регистрируется обеими половинами катушки. Поскольку они встречно намотаны, внешнее магнитное поле не создает чистого сигнала.

Существует множество более экзотических магнитометрических технологий. Магнитометры с вибрационным образцом (VSM) определяют намагниченность образца путем механической вибрации образца внутри индуктивной катушки датчика или катушки SQUID. Измеряется наведенный ток или изменяющийся поток в катушке. Магнитометрия с экстракцией импульсного поля также использует катушки для измерения намагниченности. Здесь образец закреплен и внешнее магнитное поле быстро изменяется. Затем необходимо использовать один из нескольких методов, чтобы исключить внешнее поле из того, что создает образец.