Плоский конденсатор с диэлектриком между пластинами подключен к аккумулятору не отключая конденсатор: Плоский воздушный конденсатор сдиэлектриком между пластинами подключён к аккумулятору. Физика 18014

Плоский конденсатор заполнен диэлектриком с диэлектрической. Основные расчеты емкостей

345) Два одинаковых воздушных конденсатора емкостью С0 каждый соединены последовательно. Один из конденсаторов заполняют диэлектриком с диэлектрической проницаемостью. Определите емкость батареи в этом случае:

346) Укажите формулу, определяющую работу сил электрического поля по перемещению заряда q вдоль l произвольного пути между точками 1 и 2:

347) Конденсатор зарядили до напряжения 1,2 кВ, при этом заряд на его

a) 20 пФ. обкладках оказался равным 24 нКл. Чему равна емкость конденсатора:

348) Свободный электрический диполь расположили в однородном электрическом поле, как показано на рисунке. Что будет происходить с диполем:

a) Диполь повернется против часовой стрелки.

b) Диполь останется в прежнем положении.

c) Диполь повернется по часовой стрелке.

d) Диполь будет перемещаться вправо.

e) Диполь будет перемещаться влево.

349) Потенциалы двух близких параллельных эквипотенциальных плоскостей 1 и 2 равны 3,00 В, 3,05 В. Расстояние между плоскостями 0,5 см. Определите приближенное значение модуля напряженности поля Е и укажите направление вектора напряженности электрического поля:

a) 10 В/м от 1 к 2.

b) 100 В/м от плоскости 1 к 2.

c) 0,1 В/м от 2 к 1.

d) 10 В/м от 2 к 1.

e) 0,01 В/м от 2 к 1.

350) Между пластинами заряженного плоского конденсатора поместили металлический стержень. Каково соотношение между потенциалами в точках А, В и С:

351) Какое из свойств электростатического поля указывает на то, что оно является потенциальным:

a) Работа сил поля при перемещении заряда по замкнутому контуру равна нулю.

b) Электрическое поле обладает энергией.

c) Напряженность поля в каждой точке одинакова.

d) Поле совершает работу при перемещении в нем заряженной частицы.

e) Поле оказывает силовое воздействие на заряженные тела.

352) Какую скорость приобретет заряженная частица (заряд q, масса m), пройдя в электрическом поле ускоряющую разность потенциалов U:

353) Как определяется поток вектора напряженности электрического поля через конечную поверхность S произвольной формы:

354) Сила, действующая на заряженную частицу в электрическом поле:

a) 1 и 21- сообщает частице ускорение, 2- совершает работу, изменяет энергию частицы, 3- изменяет направление движения без изменения энергии. Верно:

c) Только 2

d) Только 3

e) Только 1

355) Как определяется сила, действующая на заряженную частицу, находящуюся в электрическом поле (в общем случае):

356) Как изменится сила взаимодействия двух точечных зарядов при перенесении их из среды с относительной проницаемостью в вакуум (расстояние между зарядами r = const):

357) Три одинаковых шарика, имеющих заряды 11 мкКл, -13 мкКл и 35 мкКл, приводят в соприкосновение на короткое время, а затем вновь разводят. Какой заряд окажется на первом шарике:

a) 11 мкКл.

e) -33 мкКл.

358) Как осуществляется взаимодействие между электрическими зарядами:

a) Сила взаимодействия одного заряда на другой передается без какого либо посредника.

b) С конечной скоростью при наличии проводящей или диэлектрической среды.

c) Непосредственно при соприкосновении тел.

d) Мгновенно на любые расстояния.

e) С конечной скоростью посредством электрического поля.

359) Что такое элементарный заряд:

a) Наименьшая «порция» электрического заряда, существующего в природе.

b) Бесконечно малая порция электрического заряда dq.

c) Любой точечный заряд.

d) Единичный положительный заряд.

e) Заряд ядра атома.

360) Между пластинами заряженного плоского конденсатора поместили металлический стержень. Каково соотношение между потенциалами в точках А, В и С?

361) Аккумулятор с ЭДС E=12 В и сопротивлением r =50 мОм заряжается током I=5,0 А: Определите разность потенциалов:

a) 11. 75 B

362) Два одинаковых воздушных конденсатора емкостью С0 каждый соединены параллельно. Один из конденсаторов заполняют диэлектриком с диэлектрической проницаемостью. Определите емкость батареи в этом случае:

Физика на 100 Электродинамика Гойхман ГС

Задача 1

(Олимпиада «Физтех-2015). Две проводящие пластины с зарядами
Q
>О и -4Q расположены параллельно и напротив друг друга (см. рис.). Площадь каждой пластины
S,

размеры пластин велики по сравнению с расстоянием
d

между ними, и можно считать, что заряды распределены по каждой поверхности пластин равномерно.

1) Найти разность потенциалов левой и правой пластин.

2) Найти заряд на левой стороне левой пластины.

3) Найти силу притяжения пластин.

Решение

. Изобразим на рисунке линии напряженности электрического поля каждой пластины.
Напряжённость электрического поля между пластинами равна геометрической сумме напряжённостей составляющих полей. Видно, что направление векторов напряженностей «синих» и «красных» полей совпадает. А потому
. А разность потенциалов между пластинами равна
. Силу притяжения пластин определим по формуле
. Это справедливо, учитывая, что левая пластина находится в поле правой пластины.

Для определения заряда на левой стороне левой пластины учтём, что поля внутри металического проводника нет. Под действием поля правой пластины произойдёт перераспределение зарядов на левой и правой сторонах левой пластины (электростатическая индукция). Пусть на левой стороне левой пластины индуцируется заряд
q
, тогда на правой стороне заряд будет равен
Q
—
q
. Таким образом, внутри левой пластины создаётся, как бы, поле трех пластин: левой и правой сторон левой пластины и целиком правой пластины. Их векторная сумма равна нулю:
.

Отсюда
и
.

Ответ:

,
,

Задача 2

(Олимпиада «Физтех-2015). Три небольших по размерам положительно заряженных шарика связаны попарно тремя легкими непроводящими нитями и находятся неподвижно в вершинах равнобедренного треугольника со сторонами
a

, 2а, 2а

. Каждый из шариков, связанных короткой нитью, имеет массу
m
и заряд
q

. Третий шарик имеет массу
3m

и заряд
2q

. Короткую нить пережигают, и шарики начинают двигаться. В момент, когда шарики оказались на одной прямой, скорость шарика массой
3m

оказалась
v

.

1) Найдите в этот момент скорость двух других шариков.

2) Найдите q, считая известными
m, v, а.

Решение

. После пережигания короткой нити в результате взаимодействия только друг с другом заряженные шарики приходят в движение. Нить при этом остаётся натянутой, так как шарики все заряжены одноименным зарядом.

Рис. 1

Рис. 2

По закону сохранения импульса
. С учётом направления векторов скорости
и из соображений симметрии
.

Для нахождения заряда
q

воспользуемся законом сохранения энергии. Связанная в соответствии с рис. 1 система шаров обладает потенциальной энергией; в ней все шары взаимодействуют друг с другом попарно. Та же система шаров на рис.2 кроме попарного взаимодействия еще и движется; следовательно имеется и энергия кинетическая. Поэтому

После упрощений и с учётом
получим

Здесь

Ответ:

Задача 3

(Олимпиада «Физтех-2014).
Плос
кий воздушный
конденс
атор
ёмкостью
С
0
и
р
асстоян
и
ем межд
у о
бк
л
адками
d



за
ряж
ен до
напряжения
U

0



и
отсо
ед
инён от источника
.

Решение.

Если полагать, что расстояние
d

между пластинами значительно меньше размеров самих пластин, то поле внутри однородно и имеет напряженность, равную
. Каждая из пластин находится в поле другой пластины с напряженностью, равной
. Поэтому сила притяжения равна

.

Ёмкость плоского воздушного конденсатора определяется формулой
. Увеличение расстояния между пластинами на
сделает ёмкость конденсатора, равной
.Заряд при этом не изменится и останется равным
q
. Вначале энергия электрического поля конденсатора была равна
, а затем —
. Работа, совершённая при раздвигании обкладок, увеличила энергию конденсатора. При этом

Ответ:

Задача 4

(Олимпиада «Физтех-2011). Плоский конденсатор заряжен и отключён от источника постоянного напряжения. В конденсатор вставляют пластину из диэлектрика (см. рис.) так, что диэлектрик заполняет половину объёма конденсатора, из-за чего разность потенциалов между пластинами уменьшается в два раза.

ε

Решение.

Если конденсатор без диэлектрика равна
C

,

то накопленный на нём заряд равен
. Заполненный наполовину диэлектриком конденсатор можно представить в виде двух параллельно включённых конденсаторов: один с ёмкостью
, а второй — ёмкостью
. По условию напряжение снизилось вдвое. При этом заряд первого равен
, а заряд второго —
. При этом
. Отсюда
. Поэтому
ε=3.

Первоначально напряжённость поля равна
, где
d

— расстояние между пластинами. После ввода диэлектрика
. Таким образом,
.

Ответ:

1) уменьшилась вдвое; 2)
ε=3

Задача 5

(Олимпиада «Физтех-2011). Плоский конденсатор подключён к источнику постоянного напряжения. Не отключая источника, в конденсатор вставляют пластину из диэлектрика (см. рис.), толщина которой равна 2/3 от расстояния между пластинами конденсатора (диэлектрик заполняет 2/3 объёма конденсатора), из-за чего заряд на пластинах конденсатора увеличивается в два раза.

Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

Решение.

В отсутствии пластины из диэлектрика заряд на конденсаторе равен
. После ввода пластины этот конденсатор можно представить как два последовательно включённых конденсатора, один из которых заполнен диэлектриком. По условию ёмкость верхнего конденсатора равна
3

C

, а нижнего —
1,5ε

C

.

Тогда общая ёмкость равна
. Тогда заряд на пластинах этого конденсатора равен
. Так как по условию
, то
. Отсюда
. И, наконец, ε=4.

Так как заряд вырос в два раза, то напряженность поля в воздушном промежутке также выросла в два раза.

Ответ:

1)
увеличится в два раза; 2) ε=4.

Задача 6

(Олимпиада «Физтех-2013). Проводящий шарик радиусом
R

с зарядом
Q

имеет потенциал φ
1
=200 В. Каким станет потенциал φ
2
шарика, если он окажется внутри полого проводящего шара с радиусами сферических поверхностей
2

R

и
3

R

и зарядом
2

Q

? Центры заряженного шарика и полого шара совпадают.

q
1

q
2

Решение.

На внутренней и внешней поверхностях полого шара индуцируются заряды
q

1

и

q

2

, причём
q

1

+

q

2

=2

Q

.

Для начала определим эти индуцированные заряды. Следует напомнить, что потенциал на поверхности одиночной сферы и вне её обратно пропорционален расстоянию от центра сферы, а внутри одиночной сферы равен потенциалу на поверхности. Тогда по принципу суперпозиции полей потенциал на внешней поверхности сферического слоя

,

а на внутренней поверхности того же сферического слоя —

.

Но внутри проводника потенциал одинаковый, поэтому

Отсюда, учитывая
q

1

+

q

2

=2

Q

,

получим
q

1

=-

Q



и
q

2

=3

Q

. Тогда искомый потенциал

Ответ:

300 В

ε
2

Задача 7

(Олимпиада «Физтех-2006). Две одинаковые половинки плоского конденсатора заполнены разными диэлектриками с диэлектрическими проницаемостями ε
1
и ε
2
(см. рис.). Заряд на обкладках конденсатора равен
Q

. Определить величину и знак связанного (поляризационного) заряда верхнего диэлектрика у левой обкладки конденсатора.

Решение.

Напряжённость электрического поля между обкладками конденсатора складывается из напряжённостей полей зарядов на обкладках и поляризационного заряда диэлектрика. Для верхней половины конденсатора по принципу суперпозиции полей
. Здесь
— напряжённость в отсутствие диэлектрика при тех же зарядах
Q

, а
— напряжённость поля поляризационного заряда. Учтено, что индуцированный заряд слева на диэлектрике
отрицательный


. Аналогично в нижней половине конденсатора
. Значения
и
различны, так как при поляризации различных диэлектриков произошло перераспределение зарядов на обкладках конденсатора.

Учитывая, что
,
и
. Здесь
— заряд верхней половины пластин,
— индуцированный заряд верхнего диэлектрика, а
S
— площадь половинки обкладки. Отсюда

,

и

Аналогично

Кроме того,
и, учитывая
(разность потенциалов) или
, получим, опуская алгебраические подробности,

Ответ:

, отрицательный.

Задачи для самостоятельного решения.

Найти разность потенциалов правой и левой пластин.

Найти заряд на правой стороне левой пластины.

Найти силу отталкивания пластин.

Найти разность потенциалов левой и правой пластин.

Найти заряд на правой стороне правой пластины.

Найти силу притяжения пластин.

Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

Найдите диэлектрическую проницаемость
ε

материала диэлектрической пластины.

Ответ:

1)
уменьшилась втрое; 2)
ε=5

Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

Найдите диэлектрическую проницаемость
ε

материала диэлектрической пластины.

Ответ:

1) уменьшилась в два раза; 2)
ε=4

Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

Найдите диэлектрическую проницаемость
ε

материала диэлектрической пластины.

Ответ:

1) уменьшилась в три раза; 2)
ε=7

(Олимпиада «Физтех-2011). Плоский конденсатор подключён к источнику постоянного напряжения. Не отключая источника, в конденсатор вставляют пластину из диэлектрика (см. рис.), толщина которой равна 5/6 от расстояния между пластинами конденсатора (диэлектрик заполняет 5/6 объёма конденсатора), из-за чего заряд на пластинах конденсатора увеличивается в три раза.

Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

Найдите диэлектрическую проницаемость материала диэлектрической пластины.

Ответ:

1)
увеличится в 3 раза; 2) ε=5.

(Олимпиада «Физтех-2013). Потенциал электростатического поля в точке А на расстоянии
R

от точечного заряда
Q

равен φ
1
=300 В. Каким станет потенциал φ
2
в точке А, если заряд
Q

окажется в центре полого проводящего шара радиусами поверхностей
3

R

и
4

R

и зарядом
3

Q

Q

равен φ
1
=500 В. Каким станет потенциал φ
2
в точке А, если заряд
Q

окажется в центре полого проводящего шара радиусами поверхностей 5
R

и 7
R

и зарядом
6

S
полностью заполнен двумя слоями диэлектрика с толщинами
d
1
и
d
2
и диэлектрическими проницаемостями ε
1
и ε
2
(см. рис.). Между обкладками конденсатора поддерживается разность потенциалов
E
. Определить величину и знак связанного (поляризационного) заряда диэлектрика у нижней обкладки конденсатора.

Ответ:

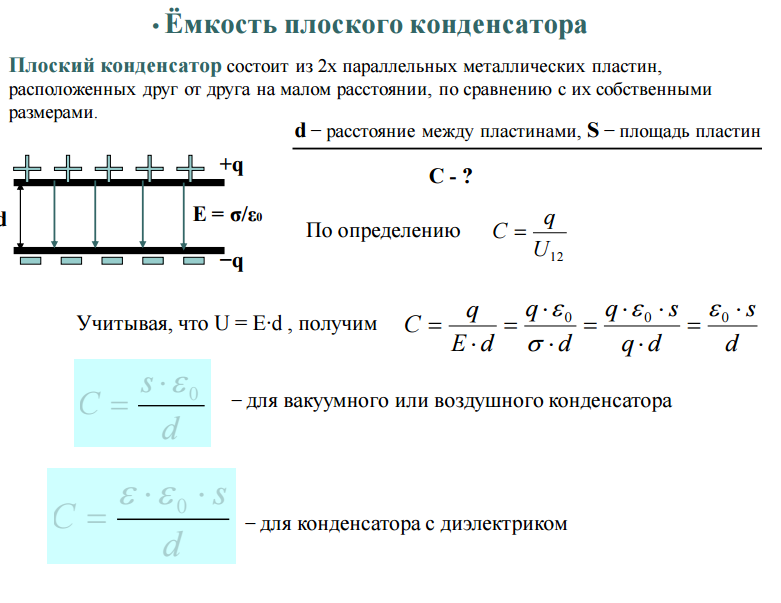
Емкость конденсатора С, имеющего две параллельно расположенные на расстоянии d друг от друга пластинки с противостоящими площадями S, когда пространство между пластинками заполнено веществом с диэлектрической проницаемостью ε, вычисляется по формуле

От материала проводящих пластинок (или обкладок) конденсатора емкость не зависит совершенно.

Пример. Чему равна емкость конденсатора, состоящего из листка парафинированной бумаги толщиною 0,1 мм, к обеим сторонам которого плотно прижаты полоски алюминиевой фольги, перекрывающие друг друга сквозь бумагу на площади в 2 см 2 . Пользуясь этими данными и табл. 1 (принимая среднее значение е для парафинированной бумаги равным 2,7), пишем

Из формулы

т. е. что в каждую емкость С может быть влит любой заряд Q, однако, если он будет велик, большим будет и напряжение Е.

При высоких напряжениях возникает опасность пробоя слоя изоляции между пластинами, что заставляет рассчитывать конденсаторы не только по емкости, но и по их диэлектрической прочности, т. е. способности выдерживать напряжения. Опасность пробоя уменьшается, если размер d не брать слишком малым и применять более стойкие диэлектрики. Конденсаторы с воздушным и жидкими диэлектриками при пробоях почти не повреждаются, так как проскочившая искра исчезает бесследно. Пробой твердых диэлектриков сопровождается образованием в них проплавленных или прожженных отверстий и полностью выводит конденсатор из строя. На конденсаторах обычно обозначена величина их емкости, а также «испытательное» и «рабочее» напряжения. Рабочее напряжение — это максимально допустимая разность потенциалов на его обкладках, при которой конденсатор может находиться долгое время, не подвергаясь опасности быть пробитым. Обычно рабочее напряжение в 2-3 раза меньше испытательного. Для большинства конденсаторов, применяемых в усилительной и приемной радиоаппаратуре, рабочее напряжение заключается в пределах 200—500 в.

Если повысить надолго напряжение на конденсаторе до испытательного значения, может наступить пробой. Поэтому испытательное напряжение иногда называют „пробивным“.

В электротехнике и радиотехнике находит применение множество разновидностей конденсаторов, в большинстве которых обкладки делаются из алюминиевой фольги, а изоляцией служит при больших емкостях парафинированная бумага, а при малых — слюда или специальные сорта керамических смесей типа „тиконд». Наряду с постоянными конденсаторами существуют переменные, емкость которых можно изменять в широких пределах. Такие конденсаторы чаще всего делают с воздушным диэлектриком и их применяют в основном в радиоприемниках (ручка настройки). Особую категорию конденсаторов образуют так называемые „электролитики » (электролитические конденсаторы), обладающие очень большими емкостями при сравнительно малых размерах и используемые исключительно лишь в цепях пульсирующего тока (см. стр. 204).

Из сочетаний нескольких конденсаторов можно образовывать различные емкости.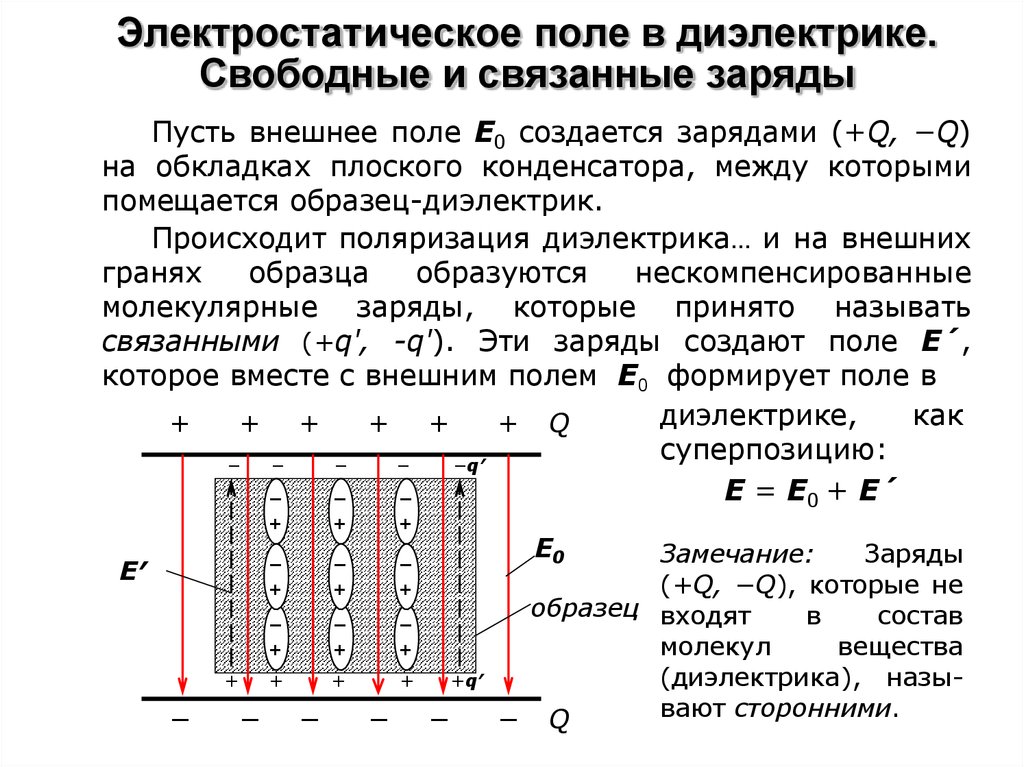

При параллельном соединении конденсаторов общая емкость группы равна сумме емкостей всех конденсаторов:

Поскольку никакая цепь не может быть прочнее самого слабого из ее звеньев, рабочее напряжение для такой группы не может быть больше рабочего напряжения самого слабого в отношении пробоя конденсатора.

При последовательном соединении расчет ведут, пользуясь обратными величинами емкостей

Эта формула не дает сразу величины общей емкости выполненного соединения, что не совсем удобно, следовательно, вычисление окончательного результата лучше вести по таким формулам, вытекающим из вышеприведенной:

для двух последовательно соединенных конденсаторов

а для трех

В смешанных соединениях конденсаторов расчет общей емкости группы легко осуществляется по отдельным участкам параллельных и последовательных соединений.

Конденсаторы разных емкостей практически соединяют последовательно в количестве более трех довольно редко, поэтому приведенные формулы почти полностью обеспечивают запросы элементарной расчетной практики.

Если все последовательно соединяемые конденсаторы совершенно одинаковы, т. е. имеют одну и ту же емкость С и рабочее напряжение Е, то при числе их, равном п,

Пример. Рассчитать общую емкость смешанного соединения конденсаторов, представленного на рис. 2 (т. е. определить емкость одного конденсатора, который может быть включен между точками А и В вместо группы из четырех конденсаторов).

Решение
, а) Определяем С» общ последовательного участка из двух конденсаторов 200 и 300 пф

б) Находим емкость С» о6ш, составленную из С» общ и параллельно присоединенного конденсатора 100 пф

С» общ = 120+ 100 = 220 пф.

Рис. 2. Соединения конденсаторов.

в) Наконец, находим С о6щ как емкость, эквивалентную последовательному соединению С» 6ш и конденсатора 220 пф. При этом воспользуемся равенством значений обеих последовательно соединяемых емкостей (число п = 2):

Электроемкость конденсатора — формула и определение

Покажем, как применять знание физики в жизни

Начать учиться

Вспышка фотоаппарата и тачскрин на телефоне невозможны без конденсаторов. Да что там — ни один современный прибор без конденсатора работать не будет. Основной параметр конденсатора — электроемкость, о которой мы и поговорим.

Электроемкость проводников

Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.

Электроемкость C = q/φ С — электроемкость [Ф] q — электрический заряд [Кл] φ — потенциал [В]

Пятерка по физике у тебя в кармане!

Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!

Конденсаторы

Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.

Конденсатор состоит из двух или более проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.

Зарядка конденсатора — это процесс накопления заряда на двух его обкладках. Заряды на них равны по величине и противоположны по знаку.

Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:

Электроемкость конденсатора C = q/U С — электроемкость [Ф] q — электрический заряд [Кл] U — напряжение (разность потенциалов) [В]

По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.

Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо сквозь диэлектрик. Такой конденсатор больше работать не будет.

Виды конденсаторов

Особенность электроемкости в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости.

Проще всего вычислить электроемкость плоского конденсатора. Плоский конденсатор состоит из двух металлических пластин, между которыми помещают диэлектрическое вещество.

Электроемкость плоского конденсатора — электроемкость [Ф] — относительная диэлектрическая проницаемость среды [—] — электрическая постоянная Ф/м — площадь пластин [м2] — расстояние между пластинами [м]

Самый популярный конденсатор — цилиндрический. Он состоит из двух металлических цилиндров, вложенных друг в друга, и диэлектрика, которым заполнено пространство между ними. Рассмотрим формулу электроемкости такого конденсатора.

Электроемкость цилиндрического конденсатора — электроемкость [Ф] — относительная диэлектрическая проницаемость среды [—] — электрическая постоянная Ф/м — длина цилиндров [м] — радиусы цилиндров [м] — функция натурального логарифма, которая зависит от радиусов цилиндров

Сферический конденсатор состоит из двух проводящих сфер, вложенных друг в друга, и непроводящей жидкости, которой заполнено пространство между ними.

Электроемкость сферического конденсатора — электроемкость [Ф] — относительная диэлектрическая проницаемость среды [—] — электрическая постоянная Ф/м — радиусы сфер [м]

Подытожим все, что узнали, на картинке-шпаргалке:

Энергия конденсатора

У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.

Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.

Энергия электростатического поля Wp = qEd Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] E — напряженность электрического поля [В/м] d — расстояние от заряда [м]

В случае с конденсатором d будет представлять собой расстояние между пластинами.

Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.

Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.

В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.

Тогда энергия конденсатора равна:

W_p = qEd/2

Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:

U = Ed

Поэтому:

W_p = qU/2

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:

Энергия конденсатора Wp = qU/2 Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] U — напряжение на конденсаторе [В]

Энергия конденсатора Wp = q2/2C Wp — энергия электростатического поля [Дж] q — электрический заряд [Кл] C — электроемкость конденсатора [Ф]

Энергия конденсатора Wp = CU2/2 Wp — энергия электростатического поля [Дж] C — электроемкость конденсатора [Ф] U — напряжение на конденсаторе [В]

Эти формулы справедливы для любого конденсатора.

Применение конденсаторов

Конденсатор есть в каждом современном устройстве. Разберем два самых наглядных примера.

Пример раз — вспышка

Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.

Пример два — тачскрин

Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.

Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.

В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.

Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.

Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.

Изучать физику на примерах из реальной жизни может быть очень даже интересно.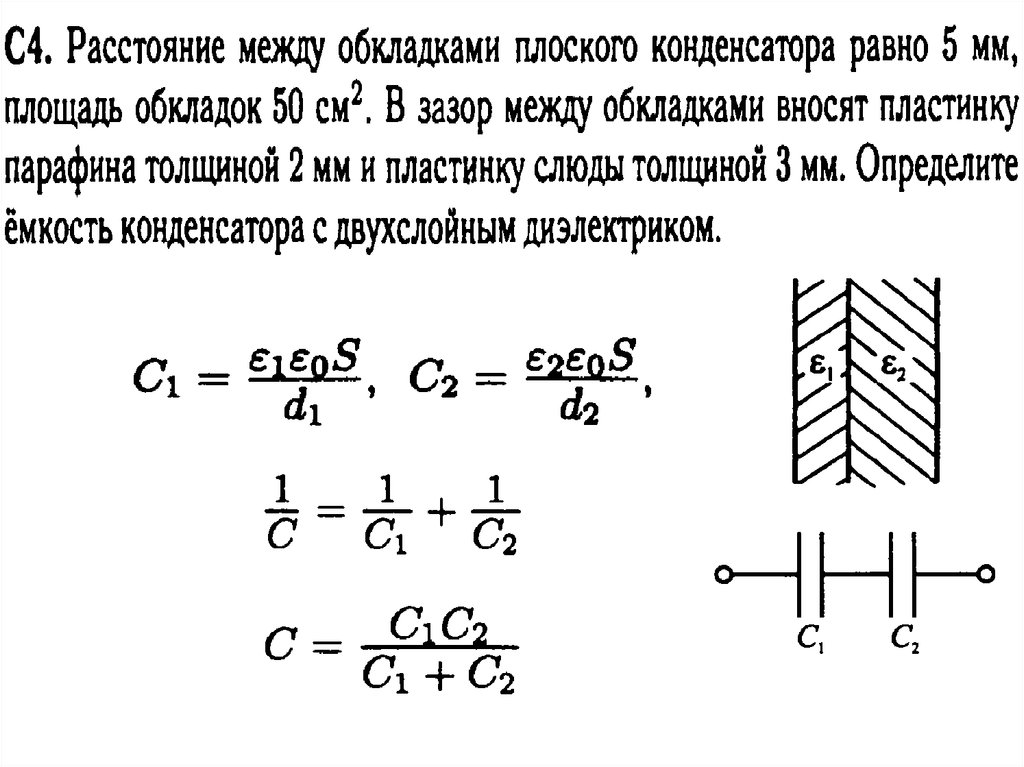 Попробуйте и убедитесь сами на классическом курсе по физике для 10 класса.

Карина Хачатурян

К предыдущей статье

Идеальный газ

К следующей статье

Ускорение свободного падения

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

8.4 Конденсатор с диэлектриком – University Physics Volume 2

Глава 8. Емкость

Цели обучения

К концу этого раздела вы сможете:

• Описывать влияние диэлектрика в конденсаторе на емкость и другие свойства
• Рассчитайте емкость конденсатора, содержащего диэлектрик

Как мы обсуждали ранее, изоляционный материал, помещенный между пластинами конденсатора, называется диэлектриком. Вставка диэлектрика между пластинами конденсатора влияет на его емкость. Чтобы понять почему, давайте рассмотрим эксперимент, описанный на рис. 8.17. Первоначально конденсатор емкостью [латекс]{C}_{0}[/латекс] при наличии воздуха между его пластинами заряжается от батареи до напряжения [латекс]{В}_{0}[/латекс]. Когда конденсатор полностью заряжен, батарея отключается. Заряд [латекс]{Q}_{0}[/латекс] остается на пластинах, и измеренная разность потенциалов между пластинами составляет [латекс]{V}_{0}[/латекс]. Теперь предположим, что мы вставляем диэлектрик, который полностью заполняет зазор между пластинами. Если мы проследим за напряжением, мы обнаружим, что показание вольтметра упало до меньшего значения В . Мы записываем это новое значение напряжения как часть исходного напряжения [латекс]{V}_{0}[/латекс], с положительным числом [латекс]\каппа[/латекс], [латекс]\каппа >1[ /латекс]:

[латекс]V=\frac{1}{\каппа}{V}_{0}.[/latex]

Константа [латекс]\каппа[/латекс] в этом уравнении называется диэлектрической проницаемостью материала между пластинами, а его значение характерно для материала. Подробное объяснение того, почему диэлектрик снижает напряжение, дано в следующем разделе. Различные материалы имеют разные диэлектрические постоянные (таблица значений для типичных материалов представлена ​​в следующем разделе). Как только батарея отключается, заряд не может течь к батарее от пластин конденсатора. Следовательно, введение диэлектрика не влияет на заряд пластины, который остается на уровне [латекс]{Q}_{0}[/латекс]. Следовательно, находим, что емкость конденсатора с диэлектриком равна

[латекс]C=\frac{{Q}_{0}}{V}=\frac{{Q}_{0}}{{V}_{0}\text{/}\kappa }=\ каппа \frac{{Q}_{0}}{{V}_{0}}=\каппа {C}_{0}.[/latex]

Это уравнение говорит нам, что емкость [латекс]{C}_{0}[/латекс] пустого (вакуумного) конденсатора может быть увеличена в раз [латекс]\каппа[/латекс] когда мы вставляем диэлектрический материал, чтобы полностью заполнить пространство между его пластинами . Обратите внимание, что уравнение 8.11 можно также использовать для пустого конденсатора, установив [латекс]\каппа =1[/латекс]. Другими словами, мы можем сказать, что диэлектрическая проницаемость вакуума равна 1, что является эталонным значением.

Рисунок 8.17  (a) При полной зарядке вакуумный конденсатор имеет напряжение [латекс]{V}_{0}[/латекс] и заряд [латекс]{Q}_{0}[/латекс] (заряды остаются на внутренних поверхностях пластины, на схеме указан знак заряда на каждой пластине). (b) На шаге 1 батарея отключена. Затем, на шаге 2, в заряженный конденсатор вставляется диэлектрик (то есть электрически нейтральный). Когда теперь измеряется напряжение на конденсаторе, обнаруживается, что значение напряжения уменьшилось до [latex]V={V}_{0}\text{/}\kappa[/latex]. На схеме указан знак индуцированного заряда, который теперь присутствует на поверхностях диэлектрического материала между пластинами.

Принцип, выраженный уравнением 8.11, широко используется в строительной отрасли (рис. 8.18). Металлические пластины в электронном искателе шипов эффективно действуют как конденсатор. Вы кладете искатель гвоздей плоской стороной на стену и непрерывно перемещаете его в горизонтальном направлении. {2}}{\kappa {C}_{0}}=\frac{1}{\kappa}{ U}_{0}.[/латекс]

Когда образец диэлектрического материала подносится к пустому заряженному конденсатору, образец реагирует на электрическое поле зарядов на обкладках конденсатора. Как мы узнали из раздела «Электрические заряды и поля по электростатике», на поверхности образца будут индуцированные заряды; однако они не являются свободными зарядами, как в проводнике, потому что в идеальном изоляторе нет свободно движущихся зарядов. Эти индуцированные заряды на поверхности диэлектрика имеют противоположный знак по отношению к свободным зарядам на пластинах конденсатора, поэтому они притягиваются свободными зарядами на пластинах. Следовательно, диэлектрик «втягивается» в зазор, а работа по поляризации диэлектрического материала между пластинами совершается за счет запасенной электрической энергии, которая уменьшается в соответствии с уравнением 8.12.

Пример

Вставка диэлектрика в изолированный конденсатор

Пустой конденсатор емкостью 20,0 пФ заряжается до разности потенциалов 40,0 В. Затем зарядная батарея отключается и вставляется кусок Teflon™ с диэлектрической проницаемостью 2,1. чтобы полностью заполнить пространство между обкладками конденсатора (см. рис. 8.17). Каковы значения (а) емкости, (б) заряда пластины, (в) разности потенциалов между пластинами и (г) энергии, запасенной в конденсаторе с диэлектриком и без него?

Стратегия

Мы определяем исходную емкость [латекс]{C}_{0}=20,0\phantom{\rule{0.2em}{0ex}}\text{пФ}[/латекс] и исходную разность потенциалов [ латекс]{V}_{0}=40,0\phantom{\rule{0.2em}{0ex}}\text{V}[/latex] между пластинами. Мы комбинируем уравнение 8.11 с другими соотношениями, включающими емкость и замену.

Решение

Показать ответ

1. Емкость увеличивается до

   [латекс]C=\каппа {C}_{0}=2,1\left(20,0\phantom{\rule{0.2em}{0ex}}\text {pF}\right)=42.0\phantom{\rule{0.2em}{0ex}}\text{pF}.[/latex]

2. Без диэлектрика заряд на пластинах равен

   [латекс]{Q}_{0}={C}_{0}{V}_{0}=\left(20. 0\phantom{\rule{0.2em} {0ex}}\text{pF}\right)\left(40.0\phantom{\rule{0.2em}{0ex}}\text{V}\right)=0.8\phantom{\rule{0.2em}{0ex }}\text{nC}.[/latex]

   Поскольку аккумулятор отсоединяется до установки диэлектрика, заряд пластины не зависит от диэлектрика и остается на уровне 0,8 нКл.

3. С диэлектриком разность потенциалов становится равной

   [латекс]V=\frac{1}{\kappa}{V}_{0}=\frac{1}{2.1}40,0\phantom{\rule{0.2em} {0ex}}\text{V}=19{2}=16,0\phantom{\rule{0.2em}{0ex}}\text{nJ}.[/latex]

   Со вставленным диэлектриком мы используем уравнение 8.12, чтобы найти, что накопленная энергия уменьшается до

   [латекс]U=\frac{1}{\kappa}{U}_{0}=\frac{1}{2.1}16.0\phantom{\rule{0.2em}{0ex}}\text{nJ} = 7,6 \ фантом {\ правило {0.2em} {0ex}} \ текст {nJ}. [/латекс]

Значение

Обратите внимание, что влияние диэлектрика на емкость конденсатора заключается в резком увеличении его емкости. Этот эффект намного глубже, чем простое изменение геометрии конденсатора.

Проверьте свое понимание

Когда диэлектрик вставлен в изолированный и заряженный конденсатор, сохраненная энергия уменьшается до 33% от первоначального значения. а) Чему равна диэлектрическая проницаемость? б) Как изменится емкость?

Показать раствор

а. 3,0; б. [латекс] C = 3,0 \ фантом {\ правило {0.2em} {0ex}} {C} _ {0} [/латекс]

Резюме

• Емкость пустого конденсатора увеличивается в [латекс]\каппа[/латекс] раз, когда пространство между его пластинами полностью заполнено диэлектриком с диэлектрической проницаемостью [латекс]\каппа[/латекс] .
• Каждый диэлектрический материал имеет свою диэлектрическую проницаемость.
• Энергия, запасенная в пустом изолированном конденсаторе, уменьшается в [латекс]\каппа[/латекс] раз, когда пространство между его пластинами полностью заполнено диэлектриком с диэлектрической проницаемостью [латекс]\каппа[/латекс].

Концептуальные вопросы

Обсудите, что произойдет, если в зазор между пластинами конденсатора вставить проводящую пластину, а не диэлектрик.

Показать решение

ответы могут отличаться

Обсудите, как изменяется энергия, хранящаяся в пустом, но заряженном конденсаторе, когда в него вставлен диэлектрик, если (а) конденсатор изолирован так, что его заряд не меняется; б) конденсатор остается подключенным к батарее, так что разность потенциалов между его обкладками не меняется.

Задачи

Показать, что для данного диэлектрического материала максимальная энергия, которую может накопить плоский конденсатор, прямо пропорциональна объему диэлектрика. 9{2}[/латекс]. а) Какова емкость этого набора пластин? (b) Если область между пластинами заполнена материалом с диэлектрической проницаемостью 6,0, какова новая емкость?

Показать раствор

а. 7,1 пФ; б. 42 пФ

Конденсатор состоит из двух концентрических сфер, одна с радиусом 5,00 см, другая с радиусом 8,00 см. а) Какова емкость этого набора проводников? б) Если пространство между проводниками заполнено материалом с диэлектрической проницаемостью 6,00, какова емкость системы?

Плоскопластинчатый конденсатор имеет заряд величиной [латекс]9,00\фантом{\правило{0,2em}{0ex}}\мю \текст{С}[/латекс] на каждой пластине и емкостью [латекс]3,00\фантом {\rule{0. 2em}{0ex}}\mu \text{F}[/latex], когда между пластинами есть воздух. Пластины разделены на 2,00 мм. При постоянном заряде пластин между пластинами вводится диэлектрик с [латекс]\каппа =5[/латекс], полностью заполняющий объем между пластинами. а) Чему равна разность потенциалов между пластинами конденсатора до и после введения диэлектрика? б) Чему равно электрическое поле в точке посередине между пластинами до и после введения диэлектрика? 9{3}.[/latex] Оцените полную энергию электрического поля, хранящуюся в стенке ячейки такого размера, если предположить, что ячейка имеет сферическую форму. ( Подсказка : Рассчитайте объем стенки ячейки.)

Конденсатор с плоскими пластинами, между пластинами которого находится только воздух, заряжается путем подключения конденсатора к батарее. Затем конденсатор отключается от батареи, при этом заряд не покидает пластины. (a) Вольтметр показывает 45,0 В, когда он подключен к конденсатору. Когда между пластинами вставлен диэлектрик, полностью заполняющий пространство, вольтметр показывает 11,5 В. Чему равна диэлектрическая проницаемость материала? б) Что покажет вольтметр, если теперь диэлектрик будет вытащен так, что он заполнит только одну треть пространства между пластинами?

Показать раствор

а. 3,91; б. 22,8 В

Глоссарий

диэлектрическая проницаемость

коэффициент, на который увеличивается емкость, когда между обкладками конденсатора вставлен диэлектрик

Лицензии и атрибуты

Конденсатор с диэлектриком. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/8-4-capacitor-with-a-dielectric. Лицензия : CC BY: Атрибуция . Условия лицензии : Скачать бесплатно на https://openstax.org/books/university-physics-volume-2/pages/1-introduction

8.5: Конденсатор с диэлектриком

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4396

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Описывать влияние диэлектрика в конденсаторе на емкость и другие свойства
• Рассчитайте емкость конденсатора, содержащего диэлектрик

Как мы обсуждали ранее, изоляционный материал, помещенный между пластинами конденсатора, называется диэлектриком. Вставка диэлектрика между пластинами конденсатора влияет на его емкость. Чтобы понять почему, давайте рассмотрим эксперимент, описанный на рисунке \(\PageIndex{1}\). Первоначально конденсатор емкостью \(C_0\) при наличии воздуха между его пластинами заряжается от батареи до напряжения \(V_0\). Когда конденсатор полностью заряжен, батарея отключается. Заряд \(Q_0\) остается на пластинах, и измеряется разность потенциалов между пластинами, равная \(V_0\). Теперь предположим, что мы вставляем диэлектрик, который полностью заполняет зазор между пластинами. Если мы проследим за напряжением, мы обнаружим, что показания вольтметра упали до меньшего значения \(В\). Мы записываем это новое значение напряжения как часть исходного напряжения \(V_0\) с положительным числом \(\каппа, \, \каппа > 1\).

\[V = \frac{1}{\kappa}V_0.\]

Постоянная \(\каппа\) в этом уравнении называется диэлектрической проницаемостью материала между пластинами, и ее значение является характеристикой материала.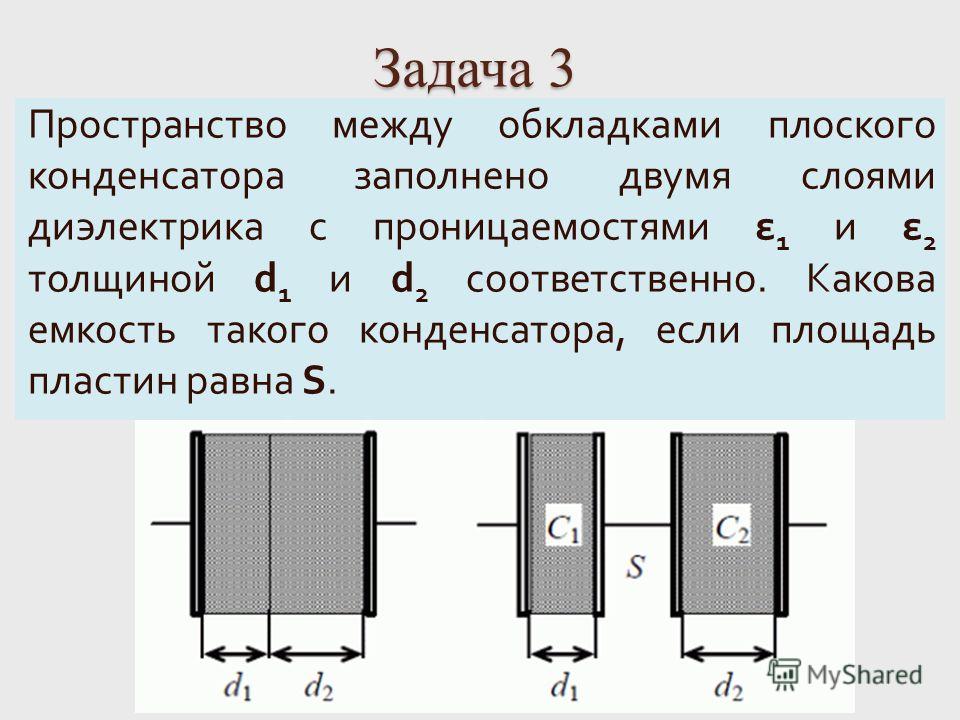 Подробное объяснение того, почему диэлектрик снижает напряжение, дано в следующем разделе. Различные материалы имеют разные диэлектрические постоянные (таблица значений для типичных материалов представлена ​​в следующем разделе). Как только батарея отключается, заряд не может течь к батарее от пластин конденсатора. Следовательно, введение диэлектрика не влияет на заряд пластины, который остается равным \(Q_0\). Следовательно, находим, что емкость конденсатора с диэлектриком равна

\[C = \frac{Q_0}{V} = \frac{Q_0}{V_0/\каппа} = \каппа \frac{Q_0}{V_0} = \каппа C_0. \метка{eq1}\]

Это уравнение говорит нам, что емкость \(C_0\) пустого (вакуумного) конденсатора может быть увеличена в \(\каппа\) раз, когда мы полностью вставляем диэлектрический материал. заполнить пространство между его пластинами . Обратите внимание, что уравнение \ref{eq1} также можно использовать для пустого конденсатора, установив \(\kappa = 1\). Другими словами, мы можем сказать, что диэлектрическая проницаемость вакуума равна 1, что является эталонным значением.

Рисунок \(\PageIndex{1}\): (a) Полностью заряженный вакуумный конденсатор имеет напряжение \(V_0\) и заряд \(Q_0\) (заряды остаются на внутренних поверхностях пластины; на схеме указан знак платы за каждую тарелку). (b) На шаге 1 батарея отключена. Затем, на шаге 2, в заряженный конденсатор вставляется диэлектрик (то есть электрически нейтральный). Когда теперь измеряется напряжение на конденсаторе, обнаруживается, что значение напряжения уменьшилось до \(V = V_0/\kappa\). На схеме указан знак индуцированного заряда, который теперь присутствует на поверхностях диэлектрического материала между пластинами.

Принцип, выраженный уравнением \ref{eq1}, широко используется в строительной отрасли (рис. \(\PageIndex{2}\)). Металлические пластины в электронном искателе шипов эффективно действуют как конденсатор. Вы кладете искатель гвоздей плоской стороной на стену и непрерывно перемещаете его в горизонтальном направлении. Когда искатель перемещается по деревянной стойке, емкость ее пластин изменяется, потому что древесина имеет другую диэлектрическую проницаемость, чем гипсовая стена. Это изменение запускает сигнал в цепи, и, таким образом, шпилька обнаруживается. 92}{\каппа C_0} = \фракция{1}{\каппа} U_0. \метка{8.12}\]

Когда образец диэлектрического материала подносится к пустому заряженному конденсатору, образец реагирует на электрическое поле зарядов на обкладках конденсатора. Как мы узнали из раздела «Электрические заряды и поля по электростатике», на поверхности образца будут индуцированные заряды; однако они не являются свободными зарядами, как в проводнике, потому что в идеальном изоляторе нет свободно движущихся зарядов. Эти индуцированные заряды на поверхности диэлектрика имеют противоположный знак по отношению к свободным зарядам на пластинах конденсатора, поэтому они притягиваются свободными зарядами на пластинах. Следовательно, диэлектрик «втягивается» в зазор, а работа по поляризации диэлектрического материала между пластинами совершается за счет запасенной электрической энергии, которая уменьшается в соответствии с уравнением \ref{8. 12}.

Пример \(\PageIndex{1}\): вставка диэлектрика в изолированный конденсатор

Пустой конденсатор емкостью 20,0 пФ заряжается до разности потенциалов 40,0 В. Затем зарядная батарея отключается, и кусок тефлона™ с диэлектрической проницаемостью 2,1 полностью заполняет пространство между обкладками конденсатора (см. рисунок \(\PageIndex{1}\)). Какие значения:

1. емкость,
2. заряд пластины,
3. разность потенциалов между пластинами, а
4. энергия, запасенная в конденсаторе с диэлектриком и без него?

Стратегия

Идентифицируем исходную емкость \(C_0 = 20,0 \, пФ\) и исходную разность потенциалов \(V_0 = 40,0 \, В\) между пластинами. Мы комбинируем уравнение \ref{eq1} с другими соотношениями, включающими емкость и замену.

Раствор

а. Емкость увеличивается до \[С = \каппа С_0 = 2,1(20,0 мкФ) = 42,0 мкФ. \номер\]

б. Без диэлектрика заряд на обкладках равен \[Q_0 = C_0V_0 = (20,0 \, пФ)(40,0 \, В) = 0,8 \, нКл. 2 = 16,0 \, нДж . \nonumber\] Со вставленным диэлектриком мы используем уравнение \ref{8.12}, чтобы найти, что накопленная энергия уменьшается до \[U = \frac{1}{\kappa}U_0 = \frac{1}{2.1} 16,0 \ , нДж = 7,6 \, нДж. \номер\]

Значение

Обратите внимание, что влияние диэлектрика на емкость конденсатора заключается в резком увеличении его емкости. Этот эффект намного глубже, чем простое изменение геометрии конденсатора.

Упражнение \(\PageIndex{1}\)

Когда диэлектрик вставлен в изолированный и заряженный конденсатор, накопленная энергия уменьшается до 33% от первоначального значения.

1. Что такое диэлектрическая проницаемость?
2. Как меняется емкость?

Ответить

а. 3,0; б. \(С = 3,0 \, С_0\)

---

Эта страница под названием 8.5: Конденсатор с диэлектриком распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа ООР или издатель

   ОпенСтакс

   Показать оглавление

   нет

2. Метки

   1. Емкость
   2. диэлектрик
   3. диэлектрическая проницаемость
   4. источник@https://openstax.