Определите линейную плотность бесконечно длинной: Трофимова задача 3.34

бесконечная длинная заряженная нить линейной плотностью

Физика
Специальный поиск
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума	Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты
	бесконечная длинная заряженная нить линейной плотностью Задача 10220 Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой τ = 20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r1 = 8 см и r2 = 12 см. Решение Задача 10690 Электрическое поле образовано бесконечно длинной нитью, заряженной с линейной плотностью t = 10 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r1 = 5 см и r2 = 10 см. Решение Задача 13427 Определите линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда Q = 1 нКл с расстояния r1 = 5 см до r2 = 2 см в направлении, перпендикулярном нити, равна 50 мкДж. Решение Задача 12950 Найти величину и направление напряженности электрического поля, созданного точечным зарядом q = 180 нКл и бесконечно длинной заряженной нитью с линейной плотностью заряда τ = 5 мкКл/м в точке, удаленной от заряда на а = 4 см, от нити на расстояние b = 3 см. Расстояние между зарядом и нитью с = 5 см. Решение Задача 14104 На расстоянии 8 см от бесконечно протяженной заряженной с поверхностной плотностью –σ = 2·10–6 Кл/м2 плоскости проведена параллельно ей бесконечно длинная нить, заряженная с линейной плотностью +τ = 8·10–7 Кл/м. Вычислить напряженность электрического поля в точке, равноотстоящей от плоскости и от нити. Решение Задача 16109 Прямая бесконечно длинная нить заряжена с линейной плотностью 32 мкКл/м. Определить величину скорости, которую приобретет точечный заряд 4 нКл массой 15·10–15 кг, перемещаясь вдоль силовой линии поля из точки, расположенной на расстоянии 4 см от нити в точку на расстоянии 15 см от нити. Начальную скорость считать равной нулю. Решение Задача 17344 Бесконечно длинная нить заряжена с линейной плотностью τ1 = 10–6 Кл/м. Перпендикулярно ей расположен стержень длиной L = 10 см. Ближайший конец стержня находится на расстоянии а = 20 см от нити. Определить силу, действующую на стержень, если он заряжен с линейной плотностью τ2 = 2·10–6 Кл/м. Решение Задача 17367 Поле образовано бесконечно длинной нитью, заряженной с линейной плотностью τ = 20·10–9 Кл/м. Определить разность потенциалов в двух точках поля, отстоящих от нити на расстояниях a = 8 см и b = 12 см. Решение Задача 19886 С какой силой Fl на единицу длины взаимодействуют две одноименно заряженные бесконечно длинные нити с линейной плотностью заряда τ1 = 0,1 мкКл/м и τ2 = 0,2 мкКл/м, находящиеся на расстоянии r1 = 10 см друг от друга? Решение Задача 22419 Электрическое поле образовано бесконечно длинной нитью, заряженной с линейной плотностью 20 нКл/м. Определить потенциал точки поля, отстоящей от нити на расстоянии 8 см. Решение Задача 23868 Найти объемную плотность энергии w электрического поля на расстоянии r = 2,0 см от бесконечно длинной нити, заряженной с линейной плотностью τ = 4,2 нКл/м. Решение Задача 24019 Электрическое поле образовано двумя бесконечно длинными нитями, заряженными с линейной плотностью 0,2 и –0,3 мкКл/м и расположенными под углом 60°. Найти величину и направление напряженности электрического поля в точке, расположенной на биссектрисе угла на расстоянии 20 см от его вершины. Решение

Напряженность поля бесконечной заряженной нити

Страница 2 из 4

21. Длинный прямой провод, расположенный в вакууме, несет заряд, равномерно распределенный по всей длине провода с линейной плотностью 2 нКл/м. Определите напряженность Е электростатического поля на расстоянии r = 1 м от провода.

22. Внутренний цилиндрический проводник длинного прямолинейного коаксиального провода радиусом R 1 = 1,5 мм заряжен с линейной плотностью τ 1 = 0,2 нКл/м. Внешний цилиндрический проводник этого провода радиусом R 2 = 3 мм заряжен с линейной плотностью τ 2 = – 0,15 нКл/м. Пространство между проводниками заполнено резиной (ε = 3). Определить напряженность электростатического поля в точках, лежащих от оси провода на расстояниях: 1) r 1 = 1 мм; 2) r 2 = 2 мм; 3) r 3 = 5 мм.

23. Электростатическое поле создается положительно заряженной с постоянной поверхностной плотностью σ = 10 нКл/м 2 бесконечной плотностью. Какую работу надо совершить для того, чтобы перенести электрон вдоль линии напряженности с расстояния r 1 = 2 см до r 2 = 1 см?

24. Электростатическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью τ = 1 нКл/см. Какую скорость приобретет электрон, приблизившись под действием поля к нити вдоль линии напряженности с расстояния r 1 = 2 см до r 2 = 1 см?

25. Одинаковые заряды Q = 100 нКл расположены в вершинах квадрата со стороной a
= 10 см. Определить потенциальную энергию этой системы.

26. В боровской модели атома водорода электрон движется по круговой орбите радиусом r = 52,8 пм, в центре которой находится протон. Определить: 1) скорость электрона на орбите; 2) потенциальную энергию электрона в поле ядра, выразив её в электрон-вольтах.

27. Кольцо радиусом r = 5 см из тонкой проволоки несет равномерно распределенный заряд Q = 10 нКл. Определить потенциал φ электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр кольца, в точке, удаленной на расстояние a
= 10 см от центра кольца.

28. На кольце с внутренним радиусом 80 см и внешним — 1м равно распределен заряд 10 нКл. Определите потенциал в центре кольца.

29. Металлический шар радиусом 5 см несет заряд Q =
10 нКл. Оп потенциал φ
электростатического поля: 1) на поверхно шара; 2) на расстоянии a
= 2 см от его поверхности.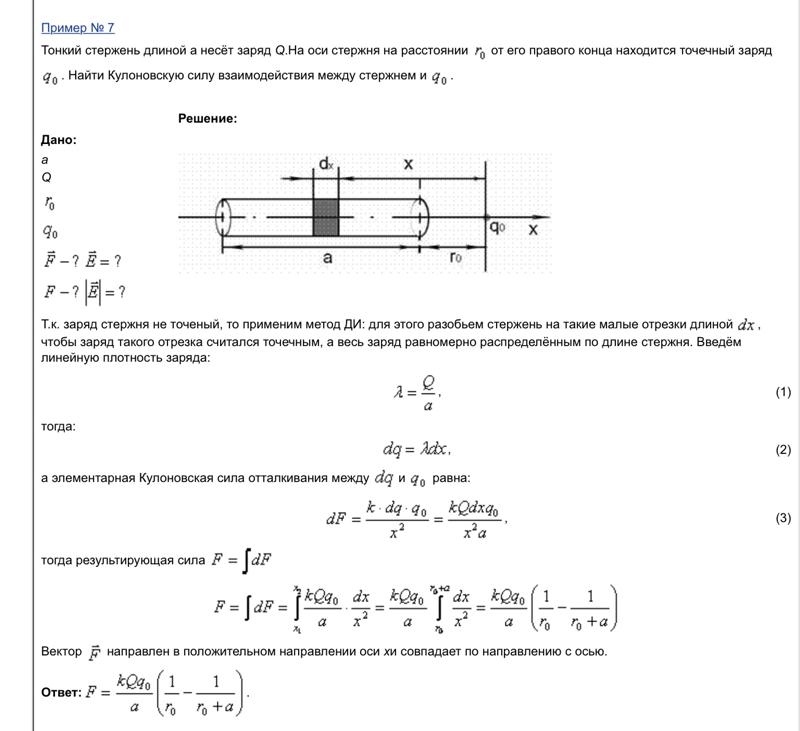 Постройте график зависимости φ(r).

30. Полый шар несет на себе равномерно распределенный заряд. Определить радиус шара, если потенциал в центре шара равен φ 1 = 200 В, а в точке, лежащей от его центра на расстоянии r = 50 см, φ 2 = 40 В.

31. Электростатическое поле создается положительным точечным зарядом. Определить числовое значение и направление градиента потенциала этого поля, если на расстоянии r = 10 см от заряда потенциал равен φ = 100 В.

32. Электростатическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью σ =
5 нКл/м 2 Определите числовое значение и направление градиента потенциала этого поля.

33. Электростатическое поле создается бесконечной прямой нитью заряженной равномерно с линейной плотностью τ = 50 пКл/см. Определите числовое значение и направление градиента потенциала в точке на расстоянии r =
0,5 м от нити.

34. Определить линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда Q = 1 нКл с расстояния r 1 = 5 см и r 2 = 2 см в направлении, перпендикулярном нити, равна 50 мкДж.

35. Электростатическое поле создается положительно заряженной бесконечной нитью Протон, двигаясь от нити под действием поля вдоль линии напряженности с расстояния r 1 = 1 см до r 2 = 5 см, изменил свою скорость от 1 до 10 Мм/с Определите линейную плотность заряда нити.

36. Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью сигма = 1 нКл/м 2 . Определить разность потенциалов между двумя точками этого поля, лежащими на расстоянии x 1 = 20 см и x 2 = 50 см от плоскости.

37. Определить поверхностную плотность зарядов на пластинах плоского слюдяного (ε = 7) конденсатора, заряженного до разности потенциалов U = 200 В, если расстояние между его пластинами равно d = 0,5 мм.

38. Электростатическое поле создается равномерно заряженной сфе поверхностью радиусом R = 10 см с общим зарядом Q = 15 нКл. Определите разность потенциалов между двумя точками этого поля, лежащими на расстояниях r 1 = 5 см и r 2 = 15 см от поверхности сферы.

39. Электростатическое поле создается сферой радиусом R = 5 см, равномерно заряженной с поверхностной плотностью сигма = 1 нКл/м 2 . Определить разность потенциалов между двумя точками поля, лежащими на расстояниях r 1 = 10 см и r 2 = 15 см от центра сферы.

40. Электростатическое поле создается равномерно заряженным шаром радиусом R=1 м с общим зарядом Q = 50 нКл. Определите разность потенциалов для точек, лежащих от центра шара на расстояниях 1) r 1 = 1,5 м и r 2 = 2 м; 2) r 1 «= 0,3 м и r 2 » = 0,8 м.

Рассмотрим
несколько примеров расчёта электростатических
полей с помощью теоремы Гаусса.

1.7.1. Поле бесконечной равномерно заряженной прямолинейной нити

Рассмотрим
равномерно заряженную бесконечно
длинную нить. Линейная плотность заряда
равна .

Заряд,
равномерно распределённый по нити,
обладает симметрией – он симметричен
относительно оси.

Нить
имеет бесконечную длину, поэтому любому
эле-ментарному зарядуdq
1
можно сопоставить другой элементарный
заряд dq
2 ,
расположенный симметрично относительно
некоторой точки в электростатическом
поле.

Поскольку
расстояние от эле-ментарных зарядов до
этой точки одинаково, модули напряжён-ностей
Е

1
и Е

2
одинаковы. Поэтому результирующая
напряжённость

Е


= Е

1 +Е

2
направлена перпен-дикулярно нити (см.
рисунок).

Очевидно,
что и в других точ-ках, расположенных
на таком же расстоянии от нити,
напря-жённость будет иметь такую же
величину и направление.

Элементарные
заряды и точка в поле были выбраны
случайно, поэтому вывод справедлив как
для всех остальных элементарных зарядов,
так и для всех точек поля.

Это
означает, что электрическое поле,
созданное заряженной нитью, симметрично
относительно оси нити. Другими словами
– симметрия поля тождественна симметрии
заряда, создающего поле.

Таким
образом, векторы напряжённости во всех
точках окружающего пространства
перпендикулярны нити и модули напряжённости
на одинаковых расстояниях от нити
одинаковы.

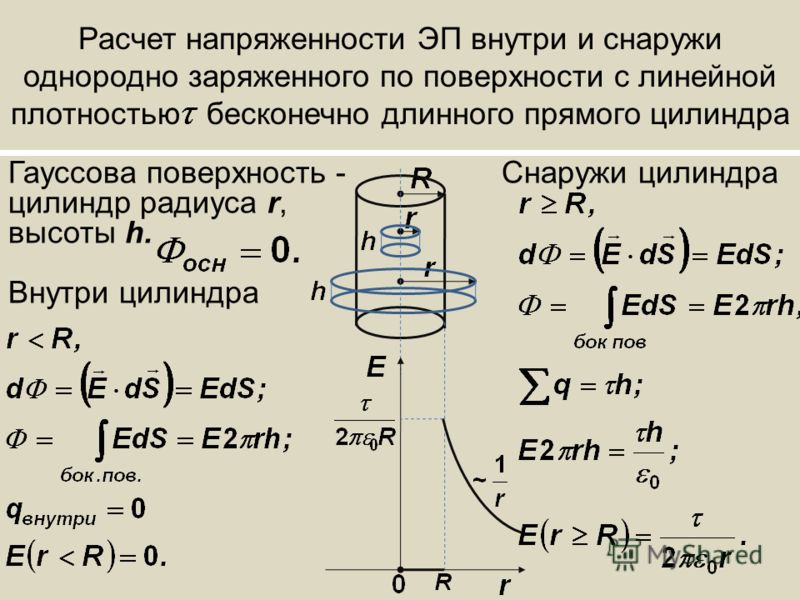
Расчёт
напряжённости поля с помощью теоремы
Гаусса следует начинать с получения
выражения для потока вектора Е

.

В
свою очередь, выражение для потока
следует начинать с выбора формы замкнутой
поверхности и её положения относительно
источника поля.

Расчёт потока
будет максимально прост, если выбрать
такую поверхность, симметрия которой
идентична симметрии создаю-щего поле
заряда.

В данном случае
удобно пользоваться замкнутой поверхностью
с осевой симметрией.

Такой
поверхностью является цилиндр, ось
которого совпадает с нитью. Пусть высота
цилиндра равна l
,
а радиус основания – r
.

Поток
вектора напряжённости поля, созданного
нитью, складывается из потока через
торцевые поверхности цилиндра и потока
через боковую поверхность.

Поток
через торцевые поверхности равен нулю,
так как векторы напряжённости
перпендикулярны нити и, соответ-ственно
угол между векторами Е


и n


равен 90 0,

.

Поток через боковую
поверхность

.

Поскольку
все точки боковой поверхности расположены
на одинаковых расстояниях от нити,
модули напряжённости во всех точках
боковой поверхности цилиндра одинаковы,
т. е.

.

Таков
вид выражения для потока вектора
рассчитываемой напряжённости.

Следующий этап
вычисления напряжённости электро-статического
поля – расчёт суммарного заряда,
охваченного замкнутой поверхностью.

Заряд,
охваченный поверхностью s
,
можно найти так:

.

Тогда, по теореме
Гаусса,

.

.

Таким образом,
напряжённость электрического поля,
создан-ного равномерно заряженной
нитью, прямо пропорциональна линейной
плотности заряда нити и обратно
пропорциональна расстоянию от нити до
интересующей нас точки.

Обратите внимание
– напряжённость обратно пропорцио-нальна
первой степени расстояния от нити
(напряжённость поля точечного заряда
обратно пропорциональна квадрату
расстояния от заряда).

Линейная
плотность заряда



– заряд, приходящийся на единицу длины:

Следовательно,

.

Разность потенциалов
между точками 1

и 2

поля, лежащими на расстоянии r
1

и r
2

от оси цилиндра:

3.
Поле заряженной сферической поверхности

Видно, что выражение
для
получилось таким же, как и для точечного
заряда.

Разность потенциалов

Шар, представляющий
собой диэлектрик, может быть внутри
равномерно заряжен с объемной плотностью

.
Поток векторачерез поверхность радиусомr

R

(R

– радиус шара) равен

Заряд
внутри сферы радиусомr
равен:

.

По теореме Гаусса

и

За пределами
равномерно заряженного шара выражение
для E
A

будет таким
же, как и полученное нами для полой сферы

,
только величинаq
будет
равняться 
V
:

Разность потенциалов
для точек, лежащих на расстоянии r

R

от центра шара:

и для точек, лежащих
на расстоянии r

R

от центра шара:

2. Проводники в электрическом поле.

Проводниками



называют тела, которые хорошо проводят
электрический ток, в которых есть
свободные электрические заряды, способные
перемещаться по всему объему проводника.

Условия
равновесия зарядов на проводнике:

Найдем величину E вблизи поверхности проводника: проведем цилиндрическую поверхность сечением dS с образующей, перпендикулярной поверхности проводника и параллельной вектору . По теореме Гаусса: , т.к поток только через одно основание цилиндра. Отсюда:

Поскольку внутри
проводника E
=0,

а в непосредственной близости от
поверхности
,
то это значит, что при переходе из
проводника в пространство за проводником
(в воздух) значениеизменяется от 0 до.

Среднее значение
напряженности поля на поверхности
проводника получается равным:

Сила, с которой
поле проводника действует на заряд,
расположенный на его поверхности dS
,
равна:

Давление, испытываемое
поверхностью проводника и обусловленное
избыточными зарядами на его поверхности,
равно:

При помещении
незаряженного проводника в электрическое
поле имеющиеся на нем заряды приходят
в движение – на противоположных
поверхностях возникают избыточные
электрические заряды противоположных
знаков.

Возникающие на
поверхности заряды создают свое поле,
которое в точности равно внешнему, но
противоположно по направлению – внутри
проводника (в полости) поле отсутствует.

Перераспределение
зарядов в проводнике под действием
внешнего поля происходит до тех пор,
пока силовые линии не окажутся
перпендикулярными поверхности проводника.

Равенство нулю
напряженности поля в полости проводника
используют для реализации электрической
защиты, причем оказалось, что электрическая
защита получается достаточно хорошей
не только в случае сплошной металлической
оболочки, но и в случае использования
мелкой металлической сетки.

Соединение
проводником какого-либо тела с землей
называют заземлением. При заземлении
заряженных проводников, в том числе и
тела человека, они теряют заряд и их
потенциал будет равен потенциалу земли.
Заземление корпусов приборов и аппаратов
способствует их безопасной эксплуатации,
т.к. исключает возможность для персонала
оказаться под напряжением корпуса
аппарата и земли.

Существует бесконечно длинная прямая нить, несущая заряд с линейной плотностью λ=0,40 мкКл/м. Вычислить потенциальную разность между точками I и 2, удаленными в η=2,0 раза дальше от резьбы, чем точка 1. Заряженной частицы в магнитном поле

21 видео

РЕКЛАМА

Текст Решение

Решение

Из теоремы Гаусса мы знаем, что электрическое поле, создаваемое бесконечно длинным прямым проводом на перпендикулярном расстоянии r от него, равно , Er=λ2πε0r, Значит, работа равна 9.0015 ∫21Erdr=∫πxxλ2πε0rdr
(где x — расстояние по перпендикуляру от резьбы, на которое от нее удалена точка 1.) Следовательно, Δφ12=λ2πε0Inη

Ответ

Пошаговое решение от экспертов, которое поможет вам в сомнениях по зазору и оценке отлично оценки на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

---

Видео по теме

Очень длинная прямая равномерно заряженная нить несет заряд λ на единицу длины. Найти величину и направление напряженности электрического поля в точке, находящейся на расстоянии y от нити и лежащей на перпендикуляре, проходящем через один из концов нити.

12306554

Очень длинная прямая нить ориентирована под прямым углом к ​​бесконечной проводящей плоскости, ее конец отстоит от плоскости на расстояние l. Нить несет однородный заряд линейной плотности λ. Предположим, что точка O является следом нити на плоскости. Найти поверхностную плотность индуцированного заряда на плоскости
(а) в точке О.
(б) в зависимости от расстояния r от точки О. линейная плотность λ. Рассчитайте разность потенциалов A и B.

13396417

Вдоль оси z лежит бесконечная нить лямбды плотности заряда. Разность потенциалов между точками A (4, 3, 4) и (3, 4, 0) равна

14277851

(а) Существует бесконечно длинная нить, равномерно заряженная с линейной плотностью заряда лямбда Кл//м . Используя закон Гаусса, рассчитайте электрическое поле (E_0) на расстоянии x от нити. (b) Теперь рассмотрим полубесконечную однородно заряженную нить (линейная плотность заряда = лямда), как показано на рисунке. Найдите y-компоненту электрического поля в точке P через E_0 . Используйте простой качественный аргумент. (c) Для ситуации, описанной в (b), рассчитайте x-компоненту электрического поля в точке P, используя метод интегрирования. (d) Найдите угол, под которым электрическое поле в точке P составляет направление x.

15159851

Текст Решение

Две одинаковые изолирующие нити расположены параллельно друг другу. Расстояние между нитями (=d) много меньше их длины. Обе нити имеют на себе одинаковую и противоположную линейную плотность заряда. Электрическое поле в точке Р, равноудаленной от нитей (в плоскости нитей) и хорошо расположенной внутри (см. рисунок), равно Е_0. Рассчитайте поле в средней точке (M) линии AB.

15159928

Текст Решение

Бесконечно длинный прямой проводник, несущий заряд с линейной плотностью +T и точечный заряд -Q, находится на определенном расстоянии друг от друга.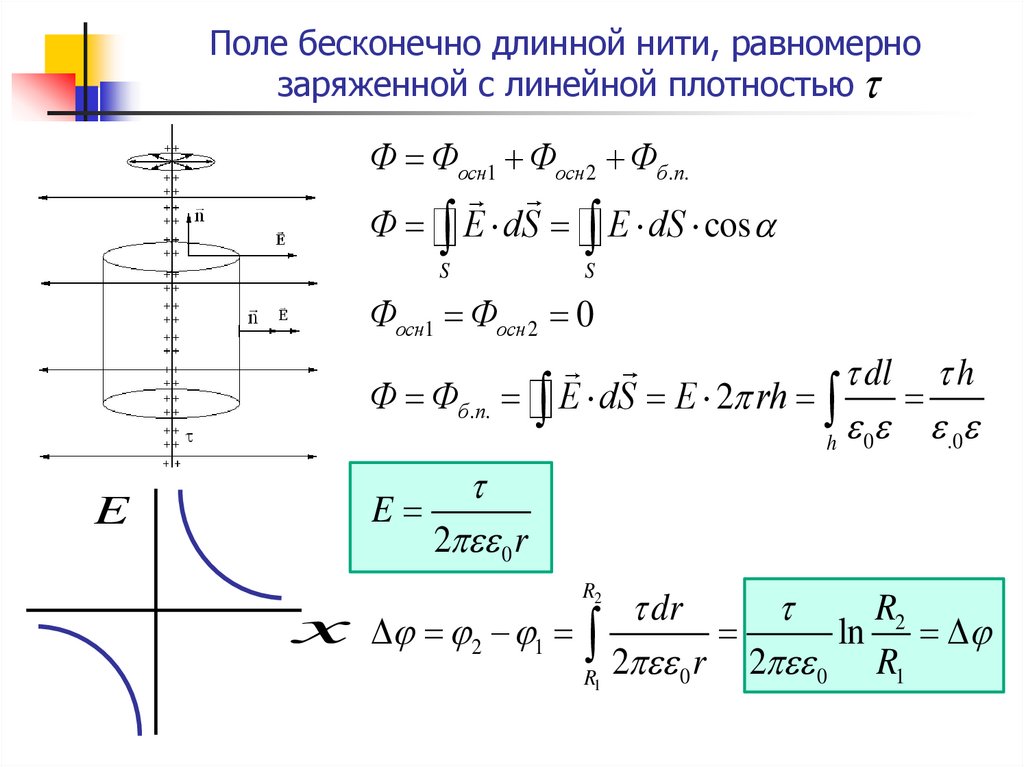 В какой из трех областей (I, II или III) находятся точки, которые (а) лежат на линии, проходящей через точечный заряд перпендикулярно проводнику. б) при котором ..th~ напряженность поля равна нулю 1)

16465249

Диполь с электрическим моментом p находится на расстоянии r от длинной нити, заряженной линейной плотностью λ . Найти силу, действующую на диполь, если а) он расположен параллельно нити , б) перпендикулярен нити . [Подсказка: поле из-за длинного потока = (1)/(2 пи эпси_(0)) (лямбда)/(r)]

17087752

Имеется бесконечно длинный прямой провод, несущий заряд линейной плотности λ=40 мкКл//м. Вычислите разность потенциалов между точками 1 и 2, если точка 2 в n=2 раз длиннее провода, чем точка 1.

17238059

Text Solution

Бесконечно длинный тонкий прямой провод имеет однородную линейную плотность заряда 13 см-1. Тогда величина силы, действующей на заряд 3 мкКл, расположенный в точке на расстоянии 18 см от провода, равна (14πε∘=9×109Nm2C−2)

233491174

Текст Решение

На рисунке показана бесконечно длинная линия линейной плотности заряда λ. Разность потенциалов VA−VB между двумя точками A и B равна

278670559

Напишите выражение для напряженности электрического поля бесконечно длинного прямого провода с линейной плотностью заряда λ в точке, находящейся на расстоянии r от это.

415575786

Текст Решение

Рассчитайте магнитное поле в точке P. На расстоянии 0,5 м от бесконечно длинного прямого провода, по которому течет ток 90 А.

435637868

Очень длинная прямая равномерно заряженная нить несет заряд λ на единицу длины. Найти величину и направление напряженности электрического поля в точке, находящейся на расстоянии y от нити и лежащей на перпендикуляре проходящей через один из концов нити.

642677895

Текст Решение

На рисунке показана бесконечно длинная линия линейной плотности заряда лямбда. Разность потенциалов V_(A)-V_(B) между двумя точками A и B равна

645067659

(a) Бесконечно длинный тонкий прямой провод имеет однородную линейную плотность заряда.

Получите выражение для электрического поля (E) в точке, лежащей на расстоянии x от точки wi

• # Электрические заряды и поля
• #CBSE 12 Класс
• #Физика
• #Школа

(a) Бесконечно длинный тонкий прямой провод имеет однородную линейную плотность заряда. Получите выражение для напряженности электрического поля (Е) в точке, расположенной на расстоянии х от провода, используя закон Гаусса.

(b) Изобразите графически изменение этого электрического поля E в зависимости от расстояния x от провода. Ответы (1)

а) Рассмотрим бесконечно длинную прямую проводник с линейной плотностью заряда

Рассмотрим цилиндрическую гауссову поверхность радиуса x и длины l.
заряд, заключенный в поверхность

По закону Гаусса

б)

Опубликовано

Safeer PP

Посмотреть полный ответ

Crack

CUET с «Лучшими учителями Индии»

• HD видео лекции
• Неограниченные пробные тесты
• Поддержка факультета

Похожие вопросы

• Является ли «процесс OXO» таким же, как «реакция KOCH», используемая для получения карбоновой кислоты?
• я выбрал ctse для медицины, но я получил его для инженерии, могу ли я изменить его
• Какая энергия преобразуется в электрическом элементном устройстве? а) Электрическая энергия в химическую энергию.